初中数学北师大版九年级下册第三章 圆4 圆周角和圆心角的关系备课课件ppt

这是一份初中数学北师大版九年级下册第三章 圆4 圆周角和圆心角的关系备课课件ppt，共17页。PPT课件主要包含了创设情境引入新课，∠A∠DCE，随堂练习巩固应用，AC5cm，∠C100°，课堂小结，布置作业等内容，欢迎下载使用。
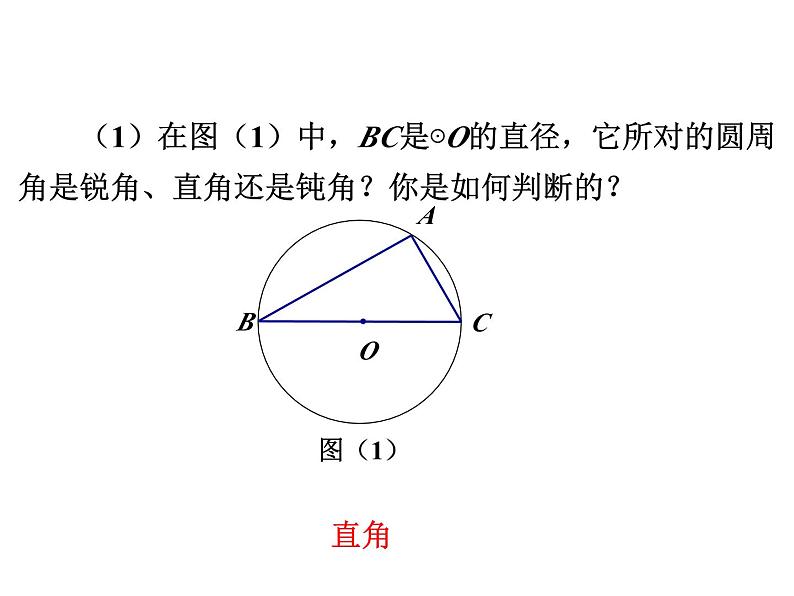
（1）在图（1）中，BC是⊙O的直径，它所对的圆周角是锐角、直角还是钝角？你是如何判断的？
（2）在图（2）中，圆周角∠BAC=90°，弦BC经过圆心O吗？
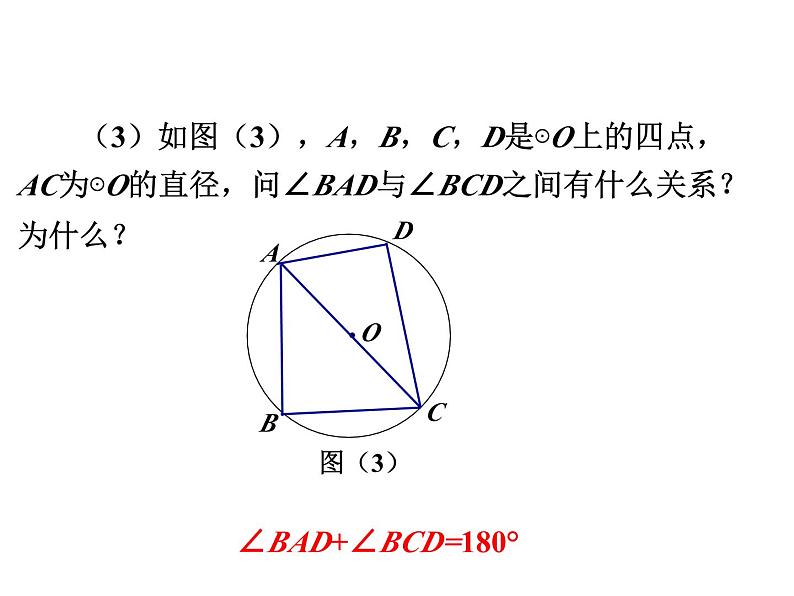
（3）如图（3），A，B，C，D是⊙O上的四点，AC为⊙O的直径，问∠BAD与∠BCD之间有什么关系？为什么？
∠BAD+∠BCD=180°
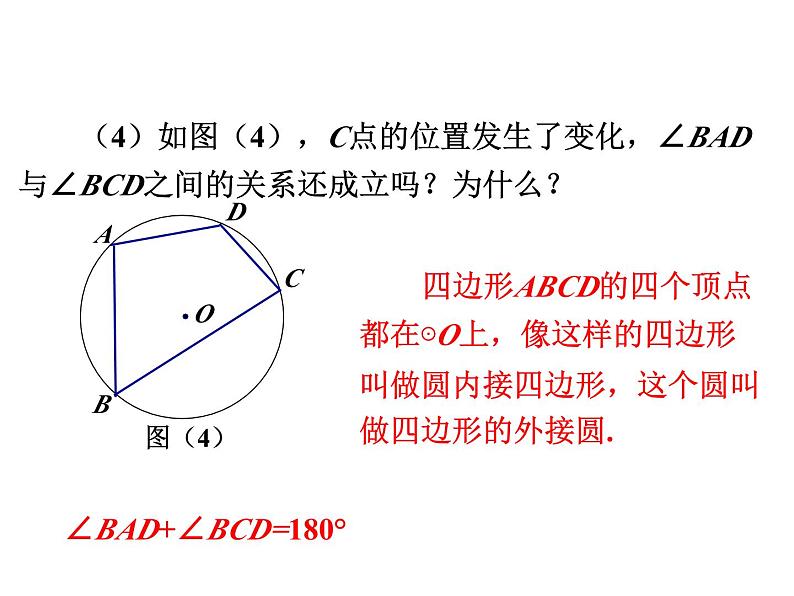
（4）如图（4），C点的位置发生了变化，∠BAD与∠BCD之间的关系还成立吗？为什么？
四边形ABCD的四个顶点都在⊙O上，像这样的四边形叫做圆内接四边形，这个圆叫做四边形的外接圆.
由以上的讨论我们可以得到：
圆内接四边形的性质1：圆内接四边形的对角互补.
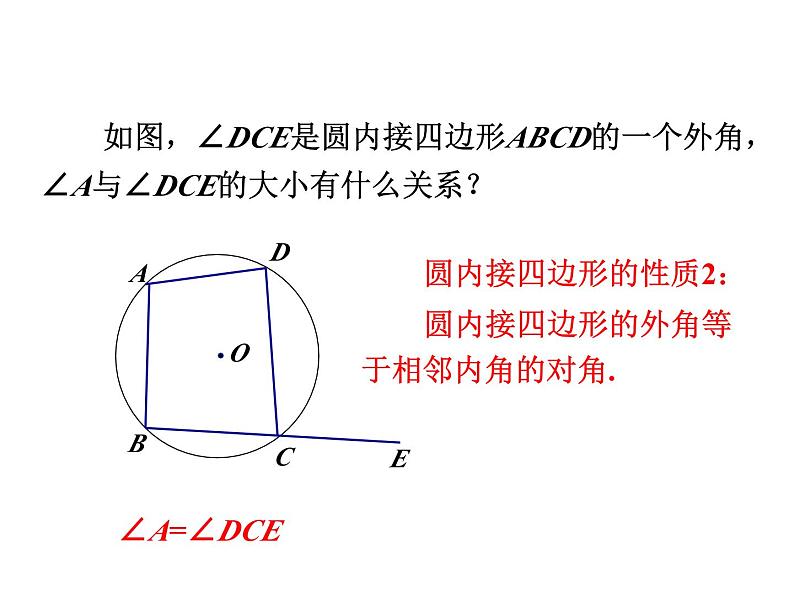
如图，∠DCE是圆内接四边形ABCD的一个外角，∠A与∠DCE的大小有什么关系？
圆内接四边形的性质2：圆内接四边形的外角等于相邻内角的对角.
归纳小结：（1）圆周角定理推论2：直径所对的圆周角是直角；90°的圆周角所对的弦是直径.（2）圆内接四边形的性质1：圆内接四边形的对角互补.（3）圆内接四边形的性质2：圆内接四边形的外角等于相邻内角的对角.
如图，∠ADB=90°；∠AED+∠B=180°，∠BAE+∠BDE=180°；∠CED=∠B，∠CDE=∠BAE.
例 如图，点A，B，C，D在⊙O上，O在∠D的内部，四边形OABC为平行四边形，求∠OAD+∠OCD的度数.
解：∵∠AOC和∠D分别是弧ABC所对的圆心角和圆周角， ∴∠AOC=2∠D. ∵四边形OABC是平行四边形， ∴∠B=∠AOC. 又∵圆内接四边形对角互补，即∠B+∠D=180°， ∴∠D=60°. 如图，连接OD，则OA=OD，OD=OC. ∴∠OAD=∠ODA ， ∠OCD=∠ODC ， ∴∠OAD+∠OCD=∠ODA+∠ODC=60°.
如图，⊙O的直径AB=10 cm，C为⊙O上一点，∠B=30°，求AC的长.
小明想用直角尺检查某些工件是否恰好为半圆形.下面所示的四种弧形，你能判断哪个是半圆形吗？为什么？
（2）为半圆形原因： 90°的圆周角所对的弦是直径.
在圆内接四边形ABCD中，对角∠A与∠C的度数之比是4 ∶ 5，求∠C的度数.
如图，在⊙O中，∠BOD=80°，求∠A和∠C的度数.
∠A= 40°，∠C= 140°
1.直径所对的圆周角是直角；90°的圆周角所对的弦是直径.2.圆内接四边形的对角互补.3.圆内接四边形的外角等于相邻内角的对角.
教材第84页习题3.5第2，3题.