江苏省昆山市娄江实验学校2022—2023学年下学期3月月考八年级数学试卷

这是一份江苏省昆山市娄江实验学校2022—2023学年下学期3月月考八年级数学试卷，共26页。试卷主要包含了函数y＝kx﹣3与y＝，若点A等内容，欢迎下载使用。
一．选择题（每题3分，共24分）
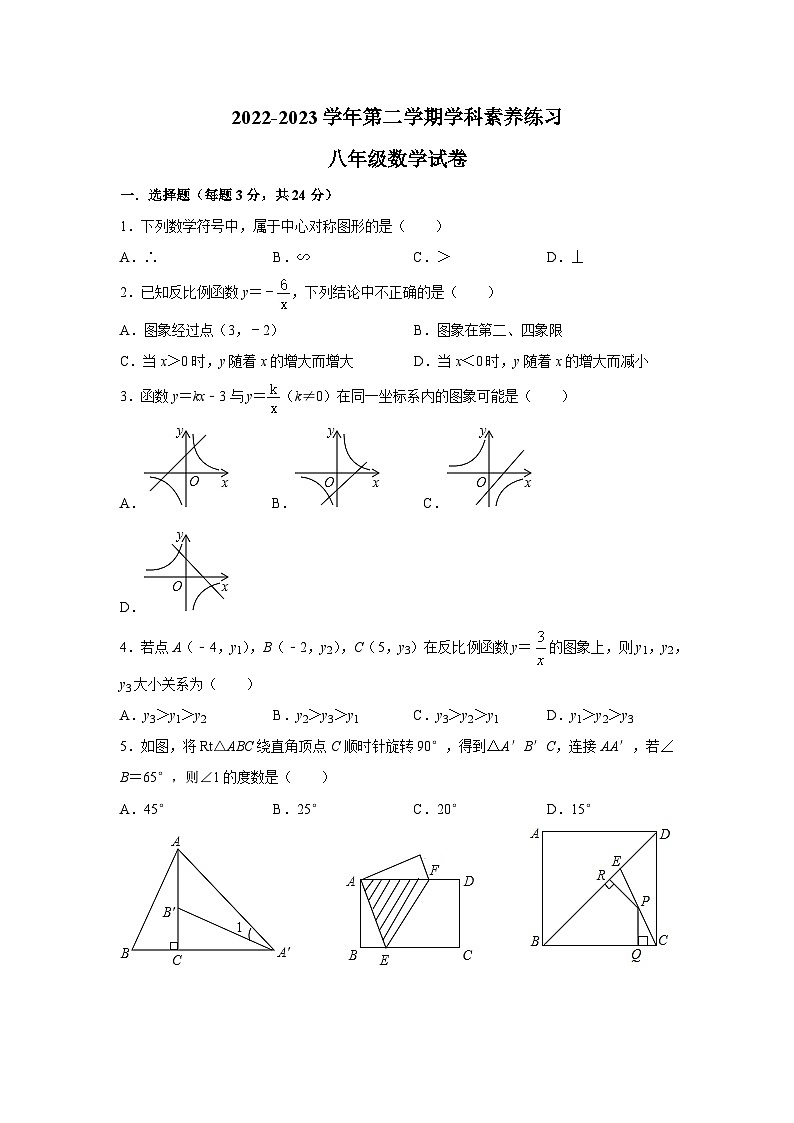
1．下列数学符号中，属于中心对称图形的是（ ）
A．∴B．∽C．＞D．⊥
2．已知反比例函数y＝﹣，下列结论中不正确的是（ ）
A．图象经过点（3，﹣2） B．图象在第二、四象限
C．当x＞0时，y随着x的增大而增大 D．当x＜0时，y随着x的增大而减小
3．函数y＝kx﹣3与y＝（k≠0）在同一坐标系内的图象可能是（ ）
A． B． C． D．
4．若点A（﹣4，y1），B（﹣2，y2），C（5，y3）在反比例函数y＝的图象上，则y1，y2，y3大小关系为（ ）
A．y3＞y1＞y2B．y2＞y3＞y1C．y3＞y2＞y1D．y1＞y2＞y3
5．如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接AA′，若∠B＝65°，则∠1的度数是（ ）
A．45°B．25°C．20°D．15°

第5题 第6题 第7题 第8题
6．在矩形纸片ABCD中，AB＝3cm，BC＝4cm，现将纸片折叠压平，使A与C重合，如果设折痕为EF，那么重叠部分△AEF的面积等于（ ）
A．B．C．D．
7．如图，E为边长为2的正方形ABCD的对角线BD上的一点，且BE＝BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值是（ ）
A．B．1C．D．2
8．如图，在菱形ABCD中，E，F分别是边CD，BC上的动点，连结AE，EF，G，H分别为AE，EF的中点，连结GH．若∠B＝60°，BC＝4，则GH的最小值为（ ）
A．2B．C．D．3
二、填空：（每空3分，共24分）
9．函数y＝的图象经过（2，﹣1），那么m＝ ．
10．已知反比例函数y＝（m为常数），若在其图象的每一个分支上，y随x增大而减小，则m的取值范围为 ．
11．如图，已知A为反比例函数y＝（x＜0）图象上的一点，过点A作AB⊥y轴，垂足为B．若△OAB的面积为1，则k的值为 ．

第11题 第12题 第13题 第15题
12．如图，在▱ABCD中，∠A＝65°，将▱ABCD绕顶点B顺时针旋转到▱A1BC1D1，当C1D1首次经过顶点C时，旋转角∠ABA1的大小为 ．
13．如图，在梯形ABCD中，AB∥CD，∠A+∠B＝90°，CD＝7，MN＝11，点M、N分别为AB、CD的中点，则线段AB＝ ．
14．已知等腰梯形的周长为80cm，中位线长与腰相等，则它的中位线长等于 cm．
15．如图，在平面直角坐标系中，点O为坐标原点，菱形ABCD的顶点B在x轴的正半轴上，点A坐标为（﹣4，0），点D的坐标为（﹣1，4），反比例函数y＝（x＞0）的图象恰好经过点C，则k的值为 ．
16．如图，点A是双曲线y＝在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰Rt△ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为 ．
三、简答题：（共11小题，共76分）
17．（本题5分）如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：
（1）以A点为旋转中心，将△ABC绕点A顺时针旋转90°得△AB1C1，画出△AB1C1．
（2）作出△ABC关于坐标原点O成中心对称的△A2B2C2．
（3）作出点C关于x轴的对称点P．若点P向右平移x个单位长度后落在△A2B2C2的内部（不含落在△A2B2C2的边上），请直接写出x的取值范围________．（提醒：每个小正方形边长为1个单位长度）
18．（本题5分）已知y＝y1﹣y2，y1与x成反比例，y2与x﹣2成正比例，并且当x＝3时，y＝5；当x＝1时，y＝﹣1．求y与x的函数表达式．
19．（本题4分）如图，两个反比例函数y＝和y＝在第一象限内的图象依次是C1和C2，设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，若四边形PAOB的面积为5，求k的值．
20．（本题6分）某标准游泳池的尺寸为长50米，宽25米，深3米，游泳池蓄水能游泳时，水深不低于1.8米．（1）该游泳池能游泳时，最低蓄水量是多少立方米？
（2）游泳池的排水管每小时排水x立方米，那么将游泳池最低蓄水量排完用了y小时．
①写出y与x的函数关系式；
②当x＝225时，求y的值；
③如果增加排水管，使每小时排水量达到s立方米，则时间y会 （选填“增大”或“减小”）．
④在②的情况下，如果最低蓄水量排完不超过5小时，每小时排水量最少增加多少立方米？
21．（本题6分）已知：如图，反比例函数y＝的图象与一次函数y＝mx+b的图象交于A（1，3），B（n，﹣1）两点．
（1）求反比例函数与一次函数的解析式；
（2）根据图象回答：当x取何值时，反比例函数的值大于一次函数的值．
22．（本题6分）如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE＝AB，连接CE．
（1）求证：BD＝EC；
（2）若∠E＝50°，求∠BAO的大小．
23．（本题7分）如图，四边形ABCD是平行四边形，AE∥BD，AE与CB的延长线交于点E，DE交AB于F．
（1）求证：BC＝BE；
（2）连接CF，若∠FDA＝∠FCB，判断四边形ABCD的形状并说明理由．
24．（本题7分）如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．
（1）求证：四边形ADCF是菱形；
（2）若AC＝5，AB＝12，求菱形ADCF的面积．
25．（本题8分）如图，在平面直角坐标系中，点A（3，2）在反比例函数的图象上，点B在OA的延长线上，BC⊥x轴，垂足为C，BC与反比例函数的图象相交于点D，连接AD．
（1）当点B的横坐标为6时，求线段AD的长；
（2）若，求点B的坐标．
26．（本题10分）如图，菱形ABCD的边长为12cm，∠A＝60°，动点P从点A出发，沿着线路AB﹣BD做匀速运动，动点Q从点D同时出发，沿着线路DC﹣CB﹣BA做匀速运动．
（1）求BD的长．
（2）已知动点P运动的速度为2cm/s，动点Q运动的速度为2.5cm/s．经过12秒后，P、Q分别到达M、N两点，试判断△AMN的形状，并说明理由．
（3）设问题（2）中的动点P、Q分别从M、N同时沿原路返回，动点P的速度不变，动点Q的速度改变为am/s，经过3秒后，P、Q分别到达E、F两点，若△BEF为直角三角形，试求a值．
27．（本题12分）如图，BC在平面直角坐标系中，已知AB＝AC，∠BAC＝90°，已知点A（﹣6，0）、C（﹣7，3），且点B在第二象限内．
（1）求点B的坐标；
（2）将△ABC以每秒3个单位的速度沿x轴向右运动，设运动时间为t秒，是否存在某一时刻，使B、C的对应点E、F，恰好落在第一象限内的反比例函数的图象上，请求出此时t的值以及这个反比例函数的解析式；
（3）在（2）的情况下，问：是否存在x轴上的点P和反比例函数图象上的点Q，使得以P、Q、E、F为顶点的四边形为平行四边形？若存在，请直接写出符合题意的点Q的坐标；若不存在，请说明理由．
【解答】解：∵当k＞0时，y＝kx﹣3过一、三、四象限，反比例函数y＝过一、三象限，
当k＜0时，y＝kx﹣3过二、三、四象限，反比例函数y＝过二、四象限，
∴B正确；
故选：B．
4．A
5．如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接AA′，若∠B＝65°，则∠1的度数是（ ）
A．45°B．25°C．20°D．15°
【分析】先利用互余计算出∠BAC＝90°﹣65°＝25°，再根据旋转的性质得∠ACA′＝90°，∠B′A′C＝∠BAC＝25°，CA＝CA′，则可判断△CAA′为等腰直角三角形得到∠CA′A＝45°，然后计算∠CA′A﹣∠B′A′C即可．
【解答】解：在Rt△ABC中，∵∠B＝65°，
∴∠BAC＝90°﹣65°＝25°，
∵Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，
∴∠ACA′＝90°，∠B′A′C＝∠BAC＝25°，CA＝CA′，
∴△CAA′为等腰直角三角形，
∴∠CA′A＝45°，
∴∠1＝∠CA′A﹣∠B′A′C＝45°﹣25°＝20°，
故选：C．
6．在矩形纸片ABCD中，AB＝3cm，BC＝4cm，现将纸片折叠压平，使A与C重合，如果设折痕为EF，那么重叠部分△AEF的面积等于（ ）
A．B．C．D．
【分析】要求重叠部分△AEF的面积，选择AF作为底，高就等于AB的长；而由折叠可知∠AEF＝∠CEF，由平行得∠CEF＝∠AFE，代换后，可知AE＝AF，问题转化为在Rt△ABE中求AE．
【解答】解：设AE＝x，由折叠可知，EC＝x，BE＝4﹣x，
在Rt△ABE中，AB2+BE2＝AE2，即32+（4﹣x）2＝x2，
解得：x＝；
由折叠可知∠AEF＝∠CEF，由AD∥BC得∠CEF＝∠AFE，
∴∠AEF＝∠AFE，即AE＝AF＝；
∴S△AEF＝×AF×AB＝××3＝．故选D．
7．如图，E为边长为2的正方形ABCD的对角线BD上的一点，且BE＝BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值是（ ）
A．B．1C．D．2
【分析】连接BP，设点C到BE的距离为h，然后根据S△BCE＝S△BCP+S△BEP求出h＝PQ+PR，再根据正方形的性质求出h即可．
【解答】解：如图，连接BP，设点C到BE的距离为h，
则S△BCE＝S△BCP+S△BEP，
即BE•h＝BC•PQ+BE•PR，
∵BE＝BC，
∴h＝PQ+PR，
∵正方形ABCD的边长为2，
∴h＝2×＝．
故选：A．
8．略
9．函数y＝的图象经过（2，﹣1），那么m＝ ﹣2 ．
【分析】利用反比例函数图象上点的坐标特征，可求出m的值，此题得解．
【解答】解：∵函数y＝的图象经过（2，﹣1），
∴m＝2×（﹣1）＝﹣2，
∴m的值为﹣2．
故答案为：﹣2．
10．已知反比例函数y＝（m为常数），若在其图象的每一个分支上，y随x增大而减小，则m的取值范围为 m＞3 ．
【分析】解不等式m﹣3＞0即可．
【解答】解：由题意可得m﹣3＞0，解得m＞3．
11．如图，已知A为反比例函数y＝（x＜0）图象上的一点，过点A作AB⊥y轴，垂足为B．若△OAB的面积为1，则k的值为 ﹣2 ．
【分析】利用反比例函数比例系数k的几何意义得到|k|＝1，然后根据反比例函数的性质确定k的值．
【解答】解：∵AB⊥y轴，
∴S△OAB＝|k|＝1，
而k＜0，
∴k＝﹣2．
故答案为﹣2．
12．如图，在▱ABCD中，∠A＝65°，将▱ABCD绕顶点B顺时针旋转到▱A1BC1D1，当C1D1首次经过顶点C时，旋转角∠ABA1的大小为 50° ．
【分析】由旋转的性质可知：▱ABCD全等于▱A1BC1D1，得出BC＝BC1，由等腰三角形的性质得出∠BCC1＝∠C1，由旋转角∠ABA1＝∠CBC1，根据等腰三角形的性质计算即可．
【解答】解：∵▱ABCD绕顶点B顺时针旋转到▱A1BC1D1，
∴BC＝BC1，
∴∠BCC1＝∠C1，
∵∠A＝65°，
∴∠C＝∠C1＝65°，
∴∠BCC1＝∠C1，
∴∠CBC1＝180°﹣2×65°＝50°，
∴∠ABA1＝50°，
故答案为：50°．
13．略
14．已知等腰梯形的周长为80cm，中位线长与腰相等，则它的中位线长等于 20 cm．
【分析】根据已知可得到上底与下底和与两腰的和相等，则中们线和等于上下底和的一半，根据周长公式即可求得中位线的长．
【解答】解：因为梯形的中位线等于上底与下底和的一半，又因为中位线长与腰相等，所以，上底与下底和与两腰的和相等，则它的中位线长等于××80＝20cm．
15．如图，在平面直角坐标系中，点O为坐标原点，菱形ABCD的顶点B在x轴的正半轴上，点A坐标为（﹣4，0），点D的坐标为（﹣1，4），反比例函数y＝（x＞0）的图象恰好经过点C，则k的值为 16 ．
【分析】要求k的值，求出点C坐标即可，由菱形的性质，再构造直角三角形，利用勾股定理，可以求出相应的线段的长，转化为点的坐标，进而求出k的值．
【解答】解：过点C、D作CE⊥x轴，DF⊥x轴，垂足为E、F，
∵ABCD是菱形，
∴AB＝BC＝CD＝DA，
易证△ADF≌△BCE，
∵点A（﹣4，0），D（﹣1，4），
∴DF＝CE＝4，OF＝1，AF＝OA﹣OF＝3，
在Rt△ADF中，AD＝，
∴OE＝EF﹣OF＝5﹣1＝4，
∴C（4，4）
∴k＝4×4＝16
故答案为：16．
16．如图，点A是双曲线y＝在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰Rt△ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为 y＝﹣（x＜0） ．
【分析】连接OC，作CD⊥x轴于D，AE⊥x轴于E，利用反比例函数的性质和等腰直角三角形的性质，根据“AAS”可判定△COD≌△OAE，设A点坐标为（a，），得出OD＝AE＝，CD＝OE＝a，最后根据反比例函数图象上点C的坐标特征确定函数解析式．
【解答】解：如图，连接OC，作CD⊥x轴于D，AE⊥x轴于E，
∵A点、B点是正比例函数图象与双曲线y＝的交点，
∴点A与点B关于原点对称，
∴OA＝OB，
∵△ABC为等腰直角三角形，
∴OC＝OA，OC⊥OA，
∴∠DOC+∠AOE＝90°，
∵∠DOC+∠DCO＝90°，
∴∠DCO＝∠AOE，
∵在△COD和△OAE中，
，
∴△COD≌△OAE（AAS），
设A点坐标为（a，），则OD＝AE＝，CD＝OE＝a，
∴C点坐标为（﹣，a），
∵﹣•a＝﹣6，
∴点C在反比例函数y＝﹣（x＜0）图象上．
故答案为：y＝﹣（x＜0）．
17．如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：
（1）以A点为旋转中心，将△ABC绕点A顺时针旋转90°得△AB1C1，画出△AB1C1．
（2）作出△ABC关于坐标原点O成中心对称的△A2B2C2．
（3）作出点C关于x轴的对称点P．若点P向右平移x个单位长度后落在△A2B2C2的内部（不含落在△A2B2C2的边上），请直接写出x的取值范围________．（提醒：每个小正方形边长为1个单位长度）
【分析】（1）利用网格特点和旋转的性质画出点B、C的对应点B1、C1，则可得到△AB1C1；
（2）根据关于原点对称的点的坐标特征写出点A2、B2、C2的坐标，然后描点即可得到△A2B2C2；
（3）先利用关于x轴的对称点的坐标特征写出P点坐标，再描点得到P点，然后观察图形可判断x的取值范围．
【解答】解：（1）如图，△AB1C1为所作；
（2）如图，△A2B2C2．为所作；
（3）如图，点P为所作；x的取值范围为5.5＜x＜8．
18．已知y＝y1﹣y2，y1与x成反比例，y2与x﹣2成正比例，并且当x＝3时，y＝5；当x＝1时，y＝﹣1．
求y与x的函数表达式．
【分析】设出解析式，利用待定系数法求得比例系数即可求得其解析式．
【解答】解：设y1＝，y2＝b（x﹣2），则y＝﹣b（x﹣2），
根据题意得，解得，
所以y关于x的函数关系式为y＝+4（x﹣2）．
19．如图，两个反比例函数y＝和y＝在第一象限内的图象依次是C1和C2，设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，若四边形PAOB的面积为5，求k的值．
【分析】根据反比例函数系数k的几何意义得到S矩形PCOD＝k，S△AOC＝S△BOD＝，然后利用四边形PAOB的面积＝S矩形PCOD﹣S△AOC﹣S△BOD进行计算．
【解答】解：∵PC⊥x轴，PD⊥y轴，
∴S矩形PCOD＝k，S△AOC＝S△BOD＝＝，
∴四边形PAOB的面积＝S矩形PCOD﹣S△AOC﹣S△BOD＝k﹣﹣＝5．
解得k＝8．
20．某标准游泳池的尺寸为长50米，宽25米，深3米，游泳池蓄水能游泳时，水深不低于1.8米．
（1）该游泳池能游泳时，最低蓄水量是多少立方米？
（2）游泳池的排水管每小时排水x立方米，那么将游泳池最低蓄水量排完用了y小时．
①写出y与x的函数关系式；
②当x＝225时，求y的值；
③如果增加排水管，使每小时排水量达到s立方米，则时间y会 减小 （选填“增大”或“减小”）．
④在②的情况下，如果最低蓄水量排完不超过5小时，每小时排水量最少增加多少立方米？
【分析】（1）根据立方体的面积公式可直接得出解；
（2）①根据每小时排水量×排水时间＝蓄水池的容积，可以得到函数关系式；
②将x＝225代入①中关系式即可求出y的值；
③根据y与x的函数关系是可得出结论；
④根据题意得出不等式，即可得出结论．
【解答】解：（1）蓄水池的最低容积是：50×25×1.8＝2250（m3）；
（2）①∵xy＝2250，y与x成反比例关系．
∴y与x之间的关系式为y＝；
②当x＝225时，y＝＝10；
③∵y＝，
∴y随x的增大而减小，
故答案为：减小；
④y＝≤5，
解得x≥450
即每小时的排水量至少为450m3；
∴450﹣225＝225，
∴每小时排水量最少增加225立方米．
21．已知：如图，反比例函数y＝的图象与一次函数y＝mx+b的图象交于A（1，3），B（n，﹣1）两点．
（1）求反比例函数与一次函数的解析式；
（2）根据图象回答：当x取何值时，反比例函数的值大于一次函数的值．
【分析】（1）反比例函数y＝的图象与一次函数y＝mx+b的图象交于A（1，3），B（n，﹣1）两点，把A点坐标代入反比例函数解析式，即可求出k，得到反比例函数的解析式．将B（n，﹣1）代入反比例函数的解析式求得B点坐标，然后再把A、B点的坐标代入一次函数的解析式，利用待定系数法求出一次函数的解析式；
（2）根据图象，分别在第一、三象限求出反比例函数的值大于一次函数的值时x的取值范围．
【解答】解：（1）∵A（1，3）在y＝的图象上，
∴k＝3，∴y＝．
又∵B（n，﹣1）在y＝的图象上，
∴n＝﹣3，即B（﹣3，﹣1）
∴
解得：m＝1，b＝2，
∴反比例函数的解析式为y＝，一次函数的解析式为y＝x+2．
（2）从图象上可知，当x＜﹣3或0＜x＜1时，反比例函数的值大于一次函数的值．
22．如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE＝AB，连接CE．
（1）求证：BD＝EC；
（2）若∠E＝50°，求∠BAO的大小．
【分析】（1）根据菱形的对边平行且相等可得AB＝CD，AB∥CD，然后证明得到BE＝CD，BE∥CD，从而证明四边形BECD是平行四边形，再根据平行四边形的对边相等即可得证；
（2）根据两直线平行，同位角相等求出∠ABO的度数，再根据菱形的对角线互相垂直可得AC⊥BD，然后根据直角三角形两锐角互余计算即可得解．
【解答】（1）证明：∵菱形ABCD，
∴AB＝CD，AB∥CD，
又∵BE＝AB，
∴BE＝CD，BE∥CD，
∴四边形BECD是平行四边形，
∴BD＝EC；
（2）解：∵平行四边形BECD，
∴BD∥CE，
∴∠ABO＝∠E＝50°，
又∵菱形ABCD，
∴AC丄BD，
∴∠BAO＝90°﹣∠ABO＝40°．
23．如图，四边形ABCD是平行四边形，AE∥BD，AE与CB的延长线交于点E，DE交AB于F．
（1）求证：BC＝BE；
（2）连接CF，若∠FDA＝∠FCB，判断四边形ABCD的形状并说明理由．
【分析】（1）根据平行四边形的性质得：AD∥BC，AD＝BC，又由平行四边形的判定得：四边形AEBD是平行四边形，又由平行四边形的对边相等可得结论；
（2）利用“有一内角为直角的平行四边形是矩形”推知四边形ABCD是矩形．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC．
∵AE∥BD，
∴四边形AEBD是平行四边形．
∴AD＝EB．
∴BC＝BE；
（2）四边形ABCD是矩形．理由如下：
∵AD∥EC，
∴∠FDA＝∠FEC．
∵∠FDA＝∠FCB，
∴∠FEC＝∠FCB，
∴FF＝FC．
又∵BC＝BE，
∴FB⊥BC，即∠ABC＝90°．
又∵四边形ABCD是平行四边形，
∴四边形ABCD是矩形．
24．如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．
（1）求证：四边形ADCF是菱形；
（2）若AC＝5，AB＝12，求菱形ADCF的面积．
【分析】（1）可先证得△AEF≌△DEB，可求得AF＝DB，可证得四边形ADCF为平行四边形，再利用直角三角形的性质可求得AD＝CD，可证得结论；
（2）根据条件可证得S菱形ADCF＝S△ABC，由三角形面积公式可求得答案．
【解答】（1）证明：∵E是AD的中点，
∴AE＝DE，
∵AF∥BC，
∴∠AFE＝∠DBE，
在△AEF和△DEB中，，
∴△AEF≌△DEB（AAS），
∴AF＝DB，
∴四边形ADCF是平行四边形，
∵∠BAC＝90°，D是BC的中点，
∴AD＝BC＝CD，
∴四边形ADCF是菱形；
（2）解：∵D是BC的中点，
∴S菱形ADCF＝2S△ADC＝S△ABC＝AB•AC＝．
25．略
26．如图，菱形ABCD的边长为12cm，∠A＝60°，动点P从点A出发，沿着线路AB﹣BD做匀速运动，动点Q从点D同时出发，沿着线路DC﹣CB﹣BA做匀速运动．
（1）求BD的长．
（2）已知动点P运动的速度为2cm/s，动点Q运动的速度为2.5cm/s．经过12秒后，P、Q分别到达M、N两点，试判断△AMN的形状，并说明理由．
（3）设问题（2）中的动点P、Q分别从M、N同时沿原路返回，动点P的速度不变，动点Q的速度改变为am/s，经过3秒后，P、Q分别到达E、F两点，若△BEF为直角三角形，试求a值．
【分析】（1）根据菱形的性质得AB＝BC＝CD＝AD，∠A＝60°，于是可判断△ABD是等边三角形，即可求得BD；
（2）如图1，根据速度公式得到12秒后点P走过的路程为24cm，则点P到达点D，即点M与D点重合，12秒后点Q走过的路程为30cm，而BC+CD＝24cm，易得点Q到达AB的中点，即点N为AB的中点，根据等边三角形的性质得MN⊥AB，即△AMN为直角三角形；
（3）由△ABD为等边三角形得∠ABD＝60°，根据速度公式得经过3秒后点P运动的路程为6cm、点Q运动的路程为3acm，所以BE＝DE＝6cm，然后分类讨论：当点Q运动到F点，且点F在NB上，如图1，则NF＝3acm，BF＝BN﹣NF＝（6﹣3a）cm，由于△BEF为直角三角形，而∠FBE＝60°，只能得到∠EFB＝90°，所以∠FEB＝30°，根据含30度的直角三角形三边的关系得6﹣3a＝×6，解得a＝1；当点Q运动到F点，且点F在BC上，如图2，则NF＝3acm，BF＝BN﹣NF＝（3a﹣6）cm，由于△BEF为直角三角形，而∠FBE＝60°，若∠EFB＝90°，则∠FEB＝30°，根据含30度的直角三角形三边的关系得3a﹣6＝×6，解得a＝3；若∠EFB＝90°，易得此时点F在点C处，则3a＝6+12，解得a＝6．
【解答】（1）解：∵四边形ABCD是菱形，
∴AD＝AB＝BC＝CD＝12，
∵∠A＝60°，
∴△ABD是等边三角形，
∴BD＝12；
（2）△AMN为直角三角形，理由如下：
如图1，12秒后点P走过的路程为2×12＝24cm，则12秒后点P到达点D，即点M与D点重合，
12秒后点Q走过的路程为2.5×12＝30cm，而BC+CD＝24cm，所以点Q到B点的距离为30﹣4＝26cm，则点Q到达AB的中点，即点N为AB的中点．
∵△ABD是等边三角形，而MN为中线，
∴MN⊥AB，
∴△AMN为直角三角形；
（3）∵△ABD为等边三角形，
∴∠ABD＝60°，
经过3秒后，点P运动的路程为6cm．点Q运动的路程为3acm，
∵点P从点M开始运动，即DE＝6cm，
∴点E为DB的中点，即BE＝DE＝6cm，
①当点Q运动到F点，且点F在NB上，如图1，则NF＝3acm，
∴BF＝BN﹣NF＝（6﹣3a）cm，
∵△BEF为直角三角形，而∠FBE＝60°，
∴∠EFB＝90°（∠FEB不能为90°，否则点F在点A的位置），
∴∠FEB＝30°，
∴BF＝BE，
∴6﹣3a＝×6，即a＝1，
②当点Q运动到F点，且点F在BC上，如图2，则NF＝3acm，
∴BF＝NF﹣BN＝（3a﹣6）cm，
∵△BEF为直角三角形，而∠FBE＝60°，
（i）若∠EFB＝90°，则∠FEB＝30°，
∴BF＝BE，
∴3a﹣6＝×6，即a＝3，
（ii）若∠FEB＝90°，即FB⊥BD，而DE＝BE，
∴点F在BD的垂直平分线上，
∴此时点F在点C处，
∴3a＝6+12，即a＝6，
综上所述，若△BEF为直角三角形，a的值为1或3或6．
27．如图，BC在平面直角坐标系中，已知AB＝AC，∠BAC＝90°，已知点A（﹣6，0）、C（﹣7，3），且点B在第二象限内．
（1）求点B的坐标；
（2）将△ABC以每秒3个单位的速度沿x轴向右运动，设运动时间为t秒，是否存在某一时刻，使B、C的对应点E、F，恰好落在第一象限内的反比例函数的图象上，请求出此时t的值以及这个反比例函数的解析式；
（3）在（2）的情况下，问：是否存在x轴上的点P和反比例函数图象上的点Q，使得以P、Q、E、F为顶点的四边形为平行四边形？若存在，请直接写出符合题意的点Q的坐标；若不存在，请说明理由．
【分析】（1）过点B作BM⊥x轴于点M，过点C作CN⊥x轴于点F，则△CAN≌△ABM，根据全等三角形的性质结合点A、C的坐标，即可求出点B的坐标；
（2）根据坐标的平移可找出点E、F的坐标，利用反比例函数图象上点的坐标特征可得出关于t的一元一次方程，解之即可得出t值，进而即可得出反比例函数的解析式；
（3）根据t的值可得出点E、F的坐标，设点P的坐标为（m，0），分EF为边及EF为对角线两种情况考虑：当EF为边时，根据平行四边形的性质结合点P在x轴上即可表示出点Q的坐标，再利用反比例函数图象上点的坐标特征即可求出m值，进而即可得出点P、Q的坐标；当EF为对角线时，根据平行四边形的对角线互相平分即可表示出点Q的坐标，再利用反比例函数图象上点的坐标特征即可求出m值，进而即可得出点P、Q的坐标．综上即可得出结论．
【解答】解：（1）过点B作BM⊥x轴于点M，过点C作CN⊥x轴于点F，如图，
∴∠CNA＝∠BMA＝90°，
∵AB＝AC，∠BAC＝90°
∴∠BAM+∠CAN＝90°．
∵∠BAM+∠ABM＝90°，
∴∠CAN＝∠ABM．
∴△CAN≌△ABM（AAS），
∴CN＝AM，AN＝BM．
∵A（﹣6，0），C（﹣7，3），
∴AN＝BM＝1，CN＝AM＝3，
OM＝3，
∴点B的坐标为（﹣3，1）．
（2）∵B（﹣3，1），C（﹣7，3），
∴E（3t﹣3，1），F（3t﹣7，3）．
∵点E、F在反比例函数的图象上，
∴3t﹣3＝3（3t﹣7），解得：t＝3，
∴3t﹣3＝6，
∴反比例函数解析式为y＝．
（3）存在，理由如下：
∵t＝3，