

江苏省苏州市昆山新镇中学2022-2023学年下学期+八年级月考数学试卷(3月)
展开
这是一份江苏省苏州市昆山新镇中学2022-2023学年下学期+八年级月考数学试卷(3月),共18页。试卷主要包含了下列说法正确的是等内容,欢迎下载使用。
1.下列图形中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
2.已知四边形ABCD,下列说法正确的是( )
A.当AD=BC,AB∥DC时,四边形ABCD是平行四边形
B.当AD=BC,AB=DC时,四边形ABCD是平行四边形
C.当AC=BD,AC平分BD时,四边形ABCD是矩形
D.当AC=BD,AC⊥BD时,四边形ABCD是正方形
3.矩形,菱形,正方形都具有的性质是( )
A.对角线相等B.对角线互相平分
C.对角线平分一组对角D.对角线互相垂直
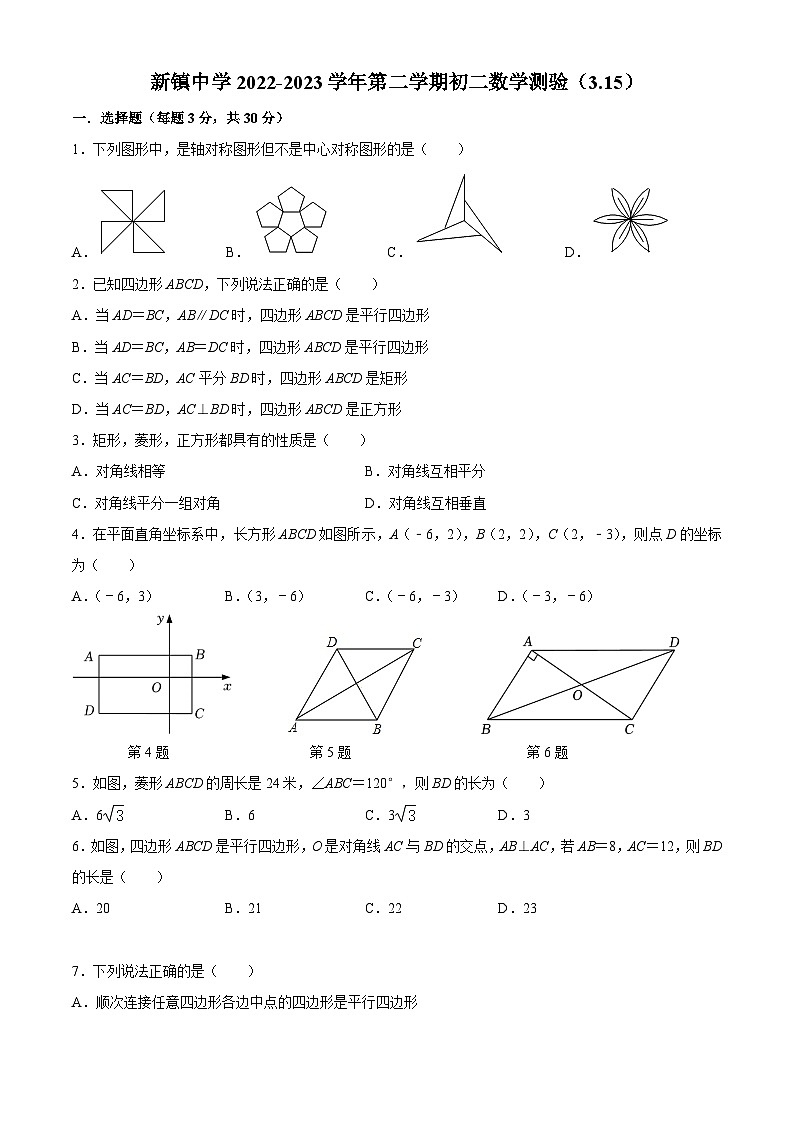
4.在平面直角坐标系中,长方形ABCD如图所示,A(﹣6,2),B(2,2),C(2,﹣3),则点D的坐标为( )
A.(﹣6,3)B.(3,﹣6)C.(﹣6,﹣3)D.(﹣3,﹣6)
第4题 第5题 第6题
5.如图,菱形ABCD的周长是24米,∠ABC=120°,则BD的长为( )
A.6B.6C.3D.3
6.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.20B.21C.22D.23
7.下列说法正确的是( )
A.顺次连接任意四边形各边中点的四边形是平行四边形
B.顺次连接任意四边形各边中点的四边形是菱形
C.顺次连接矩形各边中点的四边形是矩形
D.顺次连接菱形各边中点的四边形是正方形
8.如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )
A.65°B.60°C.50°D.40°
第8题 第9题 第10题
9.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,点F在DC的延长线上,连接AF交BC于点G,则∠FGC的度数为( )
A.67.5°B.45°C.60°D.75°
10.如图,四边形ABCD是平行四边形,点E为AB边中点,点F为对角线BD上一点,且FB=2DF,连接 DE、EF、EC,则S△DEF:S△CBE=( )
A.1:2B.1:3C.2:3D.3:4
二.填空题(每题3分,共24分)
11.如图,△ABC与△DEC关于点C成中心对称,若AB=4,则DE= .
第11题 第12题 第13题
12.如图,已知四边形ABCD是菱形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件后,使四边形ABCD成为正方形,则应该选择的是 .(仅填序号)
13.如图,在▱ABCD中,∠BCD的平分线交AD于点E,AB=3,AE=1,则BC= .
14.菱形周长为40cm,它的一条对角线长12cm,则菱形的面积为 cm2.
15.如图,在△ABC中,BC=8,D、E分别是AB、AC的中点,F是DE上一点,连接AF、BF,若AB=5,∠AFB=90°,则EF= .
16.如图,四边形ABCD中,AD=BC,E,F,G分别是AB,DC,AC的中点.若∠ACB=64°,∠DAC=22°,则∠EFG的度数为 .
第15题 第16题 第17题
17.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若BE=1,AE=2,则AC= .
18.如图,在矩形ABCD中,AB=3,AD=6,E是AD上一点,AE=1,P是BC上一动点,连接AP,取AP的中点F,连接EF,当线段EF取得最小值时,线段PD的长度是 .
三.解答题: 第18题
19.(本题10分)如图,正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求解答下列问题:
(1)△A1B1C1与△ABC关于坐标原点O成中心对称,则B1的坐标为 .
(2)△A1B1C1的面积为 .
(3)将△ABC绕某点逆时针旋转90°后,其对应点分别为A2(﹣1,﹣2),B2(1,﹣3),C2(0,﹣5),则旋转中心的坐标为 .
(4)直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标 .
20.(本题8分)如图,在▱ABCD中,∠D=45°,∠CAD=30°.求∠B和∠BAC的度数.
21.(本题8分)已知:如图,A、C是▱DEBF的对角线EF所在直线上的两点,且AE=CF.求证:四边形ABCD是平行四边形.
22.(本题8分)已知:如图,在四边形ABCD中,AB与CD不平行,E,F,G,H分别是AD,BC,BD,AC的中点.
(1)求证:四边形EGFH是平行四边形;
(2)当AB=CD,四边形EGFH是怎样的四边形?证明你的结论.
23.(本题8分)已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四边形AODE的面积.
24.(本题10分)如图,正方形ABCD中,AE=BF.
(1)求证:△BCE≌△CDF;
(2)求证:CE⊥DF;
(3)若CD=6,且DG2+GE2=41,则BE= .
25.(本题12分)在矩形纸片ABCD中,AB=6,BC=8.
(1)将矩形纸片沿BD折叠,使点A落在点E处如图①.设DE与BC相交于点F,求BF的长;
(2)将矩形纸片折叠,使点B与D重合如图②,求折痕GH的长.
26.(本题12分)已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
A.(﹣6,3)B.(3,﹣6)C.(﹣6,﹣3)D.(﹣3,﹣6)
【分析】根据长方形的性质求出点D的横坐标与纵坐标,即可得解.
【解答】解:∵四边形ABCD是长方形,
∴AB∥DC,AD∥BC,
∵A(﹣6,2),B(2,2),C(2,﹣3),
∴点D的横坐标与点A的横坐标相同,为﹣6,
点D的纵坐标与点C的纵坐标相同,为﹣3,
∴点D的坐标为(﹣6,﹣3).
故选:C.
5.B
6.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.20B.21C.22D.23
【分析】由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
【解答】解:∵四边形ABCD是平行四边形,AC=12,
∴OA=AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB==10,
∴BD=2OB=20.
故选:A.
7.下列说法正确的是( )
A.顺次连接任意四边形各边中点的四边形是平行四边形
B.顺次连接任意四边形各边中点的四边形是菱形
C.顺次连接矩形各边中点的四边形是矩形
D.顺次连接菱形各边中点的四边形是正方形
【分析】根据“三角形中位线定理,平行四边形、菱形、矩形以及正方形的判定方法”进行分析判断.
【解答】解:A、顺次连接任意四边形各边中点得到的四边形是平行四边形,原说法正确;
B、顺次连接对角线相等的四边形各边中点的四边形是菱形,原说法错误;
C、顺次连接矩形各边中点形成的四边形是菱形,原说法错误;
D、顺次连接菱形各边中点,所形成的四边形是矩形,原说法错误.
故选:A.
8.如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )
A.65°B.60°C.50°D.40°
【分析】先利用互余计算出∠BAC=65°,再利用旋转的性质得CA=CA′,∠A′=∠BAC=65°,∠ACA′等于旋转角,根据等腰三角形的性质和三角形内角和计算出∠ACA′的度数即可.
【解答】解:∵∠ACB=90°,∠ABC=25°,
∴∠BAC=65°,
∵以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,
∴CA=CA′,∠A′=∠BAC=65°,∠ACA′等于旋转角,
∴∠CAA′=∠A′=65°,
∴∠ACA′=180°﹣65°﹣65°=50°,
即旋转角的度数为50°.
故选:C.
9.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,点F在DC的延长线上,连接AF交BC于点G,则∠FGC的度数为( )
A.67.5°B.45°C.60°D.75°
【分析】由正方形的性质和菱形的性质可得∠CAB=45°=∠ACB,∠ABC=90°,∠CAF=∠EAF=∠CAB=22.5°,由三角形的外角性质可求解.
【解答】解:∵四边形ABCD是正方形,
∴∠CAB=45°=∠ACB,∠ABC=90°,
∵四边形AEFC是菱形,
∴∠CAF=∠EAF=∠CAB=22.5°,
∴∠FGC=∠ACB+∠CAF=67.5°,
故选:A.
10.如图,四边形ABCD是平行四边形,点E为AB边中点,点F为对角线BD上一点,且FB=2DF,连接 DE、EF、EC,则S△DEF:S△CBE=( )
A.1:2B.1:3C.2:3D.3:4
故答案为:②.
13.如图,在▱ABCD中,∠BCD的平分线交AD于点E,AB=3,AE=1,则BC= 4 .
【分析】证出∠DEC=∠ECD,得出DE=CD=3,进而得出答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=3,AD=BC,
∴∠DEC=∠BCE,
∵CE平分∠BCD,
∴∠BCE=∠ECD,
∴∠DEC=∠ECD,
∴DE=CD=3,
∴BC=AD=AE+DE=1+3=4;
故答案为:4.
14.菱形周长为40cm,它的一条对角线长12cm,则菱形的面积为 96 cm2.
【分析】画出草图分析.因为周长是40,所以边长是10.根据对角线互相垂直平分得直角三角形,运用勾股定理求另一条对角线的长,最后根据菱形的面积等于对角线乘积的一半计算求解.
【解答】解:因为周长是40cm,所以边长是10cm.
如图所示:AB=10cm,AC=12cm.
根据菱形的性质,AC⊥BD,AO=6cm,
∴BO=8cm,BD=16cm.
∴面积S=×16×12=96(cm2).
故答案为96
15.如图,在△ABC中,BC=8,D、E分别是AB、AC的中点,F是DE上一点,连接AF、BF,若AB=5,∠AFB=90°,则EF= 1.5 .
【分析】根据三角形中位线定理求出DE,根据直角三角形斜边上的中线的性质求出DF,计算即可.
【解答】解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE=BC=4,
在Rt△ABC中,AB=5,∠AFB=90°,D是AB的中点,
∴DF=AB=2.5,
∴EF=DE﹣DF=1.5,
故答案为:1.5.
16.如图,四边形ABCD中,AD=BC,E,F,G分别是AB,DC,AC的中点.若∠ACB=64°,∠DAC=22°,则∠EFG的度数为 21° .
【分析】根据三角形中位线定理和等腰三角形等边对等角的性质求解即可.
【解答】解:∵AD=BC,E,F,G分别是AB,CD,AC的中点,
∴GF是△ACD的中位线,GE是△ACB的中位线.
∴GF∥AD且GF=AD,GE∥BC且GE=BC.
又∵AD=BC,
∴GF=GE,∠FGC=∠DAC=22°,∠AGE=∠ACB=64°.
∴∠EFG=∠FEG.
∵∠FGE=∠FGC+∠EGC=22°+(180°﹣64°)=138°,
∴∠EFG=(180°﹣∠FGE)=21°.
故答案是:21°.
17.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若BE=1,AE=2,则AC= 5 .
【分析】由矩形的性质得出OA=OB,设OA=OB=x,则OE=x﹣1,在Rt△AOE中,由勾股定理得出方程,解方程求出OA,即可得出答案.
【解答】解:∵四边形ABCD是矩形,
∴OA=OC=AC,OB=OD=BD,AC=BD,
∴OA=OB,
设OA=OB=x,则OE=x﹣1,
∵AE⊥BD,
∴∠AEO=90°,
【分析】(1)根据关于原点成中心对称的点的特征求救;
(2)利用割补法求三角形的面积;
(3)利用作图观察求解.
【解答】解:(1)∵B(﹣2,﹣2),
∴B1(2,2).
故答案为:(2,2).
(2)△A1B1C1的面积为:××=2.5
故答案为:2.5.
(3)根据旋转的性质,旋转中心在对称点的连线的垂直平分线上,所以两对对称点的垂直平分线的交点就是旋转中心.
所以旋转中心的坐标为:(0,﹣1).
故答案为:(0,﹣1).
20.如图,在▱ABCD中,∠D=45°,∠CAD=30°.求∠B和∠BAC的度数.
【分析】根据平行四边形的性质可知:∠D=∠B=45°,AB∥CD,得出∠BAD+∠D=180°,求出∠BAD的度数,即可得出∠BAC的度数.
【解答】解:∵四边形ABCD为平行四边形,
∴∠B=∠D=45°,AB∥CD,
∴∠BAD+∠D=180°,
∴∠BAD=180°﹣45°=135°,
∴∠BAC=∠BAD﹣∠CAD=135°﹣30°=105°.
21.已知:如图,A、C是▱DEBF的对角线EF所在直线上的两点,且AE=CF.求证:四边形ABCD是平行四边形.
【分析】如图,连接BD,交AC于点O,欲证明证明四边形ABCD是平行四边形,只需证得AO=CO,DO=BO.
【解答】证明:如图,连接BD,交AC于点O.
∵四边形DEBF是平行四边形,
∴OD=OB,OE=OF.
又∵AE=CF,
∴AE+OE=CF+OF,即OA=OC,
∴四边形ABCD是平行四边形.
22.已知:如图,在四边形ABCD中,AB与CD不平行,E,F,G,H分别是AD,BC,BD,AC的中点.
(1)求证:四边形EGFH是平行四边形;
(2)当AB=CD,四边形EGFH是怎样的四边形?证明你的结论.
【分析】(1)根据三角形中位线定理得到EG=AB,EG∥AB,FH=AB,FH∥AB,根据平行四边形的判定定理证明结论;
(2)依据四边形ABCD是平行四边形,再运用三角形中位线定理证明邻边相等,从而证明它是菱形.
【解答】(1)证明:∵E,G分别是AD,BD的中点,
∴EG是△DAB的中位线,
∴EG=AB,EG∥AB,
同理,FH=AB,FH∥AB,
∴EG=FH,EG∥FH,
∴四边形EGFH是平行四边形;
(2)菱形.理由:
∵F,G分别是BC,BD的中点,
∴FG是△DCB的中位线,
∴FG=CD,FG∥CD,
又∵EG=AB,
∴当AB=CD时,EG=FG,
∴平行四边形EGFH是菱形.
23.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四边形AODE的面积.
【分析】(1)根据菱形的性质得出AC⊥BD,再根据平行四边形的判定定理得四边形AODE为平行四边形,∵∠BCE+∠DCG=90°,
∴∠CDF+∠DCG=90°,
∴∠DGC=90°,
∴CE⊥DF;
(3)解:连接DE,
∵∠DGE=90°,
∴DG2+EG2=DE2,
∵DG2+GE2=41,
∴DE2=41,
在Rt△ADE中,由勾股定理得,AE===,
∴BE=AB﹣AE=6﹣.
故答案为:6﹣.
25.在矩形纸片ABCD中,AB=6,BC=8.
(1)将矩形纸片沿BD折叠,使点A落在点E处如图①.设DE与BC相交于点F,求BF的长;
(2)将矩形纸片折叠,使点B与D重合如图②,求折痕GH的长.
【分析】(1)根据折叠的性质可得∠ADB=∠EDB,再根据两直线平行,内错角相等可得∠ADB=∠DBC,然后求出∠FBD=∠FDB,根据等角对等边可得BF=DF,设BF=x,表示出CF,在Rt△CDF中,利用勾股定理列出方程求解即可;
(2)根据折叠的性质可得DH=BH,设BH=DH=x,表示出CH,然后在Rt△CDH中,利用勾股定理列出方程求出x,再连接BD、BG,根据翻折的性质可得BG=DG,∠BHG=∠DHG,根据两直线平行,内错角相等求出∠BHG=∠DGH,然后求出∠DHG=∠DGH,根据等角对等边可得DH=DG,从而求出四边形BHDG是菱形,再利用勾股定理列式求出BD,然后根据菱形的面积列出方程求解即可.
【解答】解:(1)由折叠得,∠ADB=∠EDB,
∵矩形ABCD的对边AD∥BC,
∴∠ADB=∠DBC,
∴∠FBD=∠FDB,
∴BF=DF,
设BF=x,则CF=8﹣x,
在Rt△CDF中,CD2+CF2=DF2,
即62+(8﹣x)2=x2,
解得x=;
(2)由折叠得,DH=BH,设BH=DH=x,
则CH=8﹣x,
在Rt△CDH中,CD2+CH2=DH2,
即62+(8﹣x)2=x2,
解得x=,
连接BD、BG,
由翻折的性质可得,BG=DG,∠BHG=∠DHG,
∵矩形ABCD的边AD∥BC,
∴∠BHG=∠DGH,
∴∠DHG=∠DGH,
∴DH=DG,
∴BH=DH=DG=BG,
∴四边形BHDG是菱形,
在Rt△BCD中,BD===10,
S菱形BHDG=BD•GH=BH•CD,
即×10•GH=×6,
解得GH=.
26.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
【分析】(1)先证明四边形AFCE为平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判定;根据勾股定理即可求得AF的长;
(2)①分情况讨论可知,当P点在BF上、Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;
②分三种情况讨论可知a与b满足的数量关系式.
【解答】解:(1)①∵四边形ABCD是矩形,
相关试卷
这是一份2023-2024学年江苏省苏州市昆山市昆山通海实验中学八年级(上)10月月考数学试卷(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年江苏省苏州市昆山市新镇中学八年级(上)月考数学试卷(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年江苏省苏州市昆山市葛江中学八年级(上)10月月考数学试卷(含解析),共22页。试卷主要包含了平方根等于它本身的数是,如图是小明的答卷,他的得分应是等内容,欢迎下载使用。








