
+山东省烟台市莱州市2023-2024学年九年级上学期期末数学试卷(五四制)+
展开
这是一份+山东省烟台市莱州市2023-2024学年九年级上学期期末数学试卷(五四制)+,共31页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.如图,将三棱柱的一个角切割掉,所得几何体的左视图为( )
A.B.C.D.
2.若sin(α+20°)=cs50°,则α的度数是( )
A.50°B.40°C.30°D.20°
3.若A(2,4)与B(﹣2,a)都是反比例函数y=(k≠0)图象上的点,则a的值是( )
A.4B.﹣4C.2D.﹣2
4.如图,在⊙O中,AB是直径,弦AC=5,∠BAC=∠D.则AB的长为( )
A.5B.10C.5D.10
5.二次函数y=ax2+bx+c(a≠0)的图象的顶点坐标是(﹣2,﹣1),且图象与y轴交于点(0,﹣9).将该二次函数的图象以原点为旋转中心旋转180°,则旋转后得到的函数表达式为( )
A.y=﹣2(x+2)2﹣1B.y=﹣2(x+2)2+1
C.y=2(x﹣2)2+1D.y=2(x﹣2)2﹣1
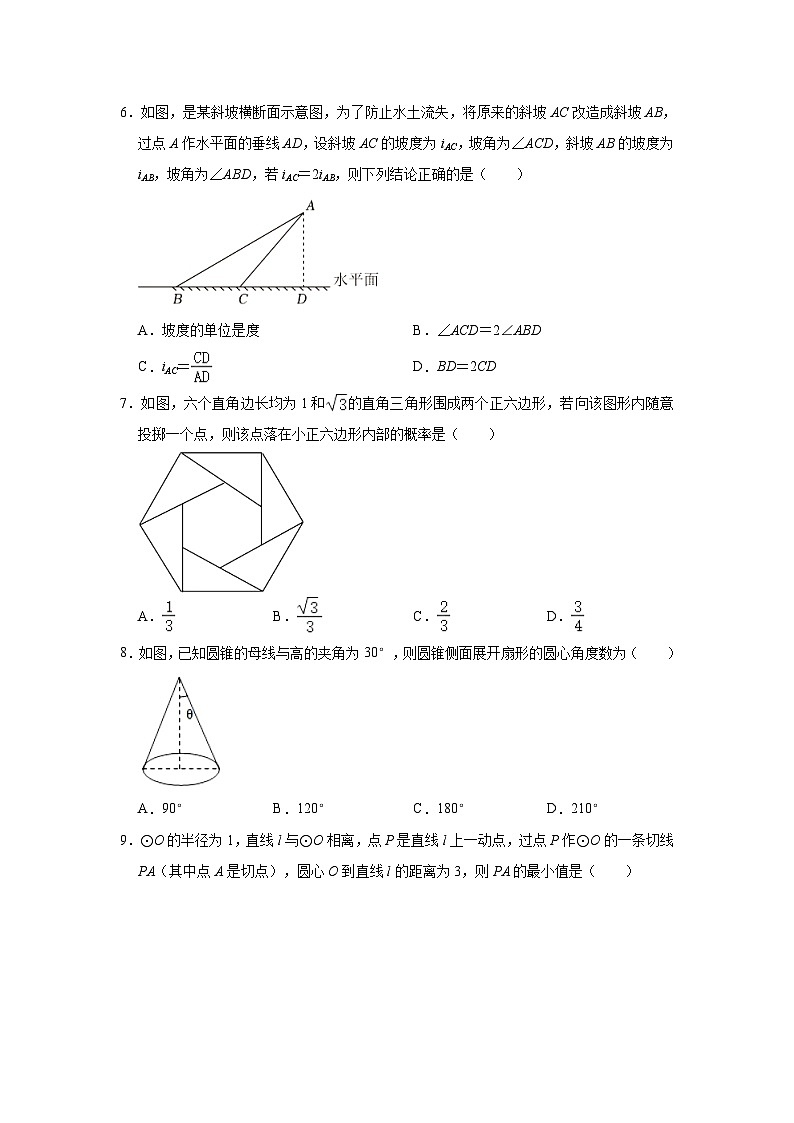
6.如图,是某斜坡横断面示意图,为了防止水土流失,将原来的斜坡AC改造成斜坡AB,过点A作水平面的垂线AD,设斜坡AC的坡度为iAC,坡角为∠ACD,斜坡AB的坡度为iAB,坡角为∠ABD,若iAC=2iAB,则下列结论正确的是( )
A.坡度的单位是度B.∠ACD=2∠ABD
C.iAC=D.BD=2CD
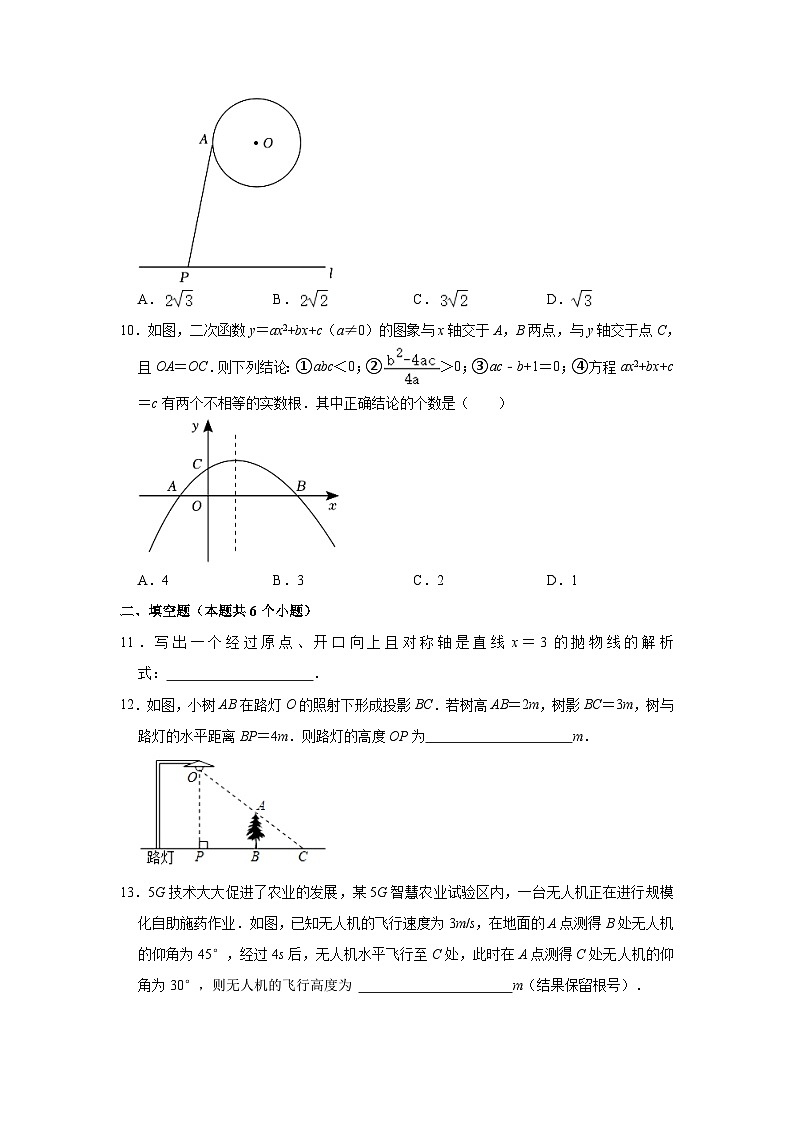
7.如图,六个直角边长均为1和的直角三角形围成两个正六边形,若向该图形内随意投掷一个点,则该点落在小正六边形内部的概率是( )
A.B.C.D.
8.如图,已知圆锥的母线与高的夹角为30°,则圆锥侧面展开扇形的圆心角度数为( )
A.90°B.120°C.180°D.210°
9.⊙O的半径为1,直线l与⊙O相离,点P是直线l上一动点,过点P作⊙O的一条切线PA(其中点A是切点),圆心O到直线l的距离为3,则PA的最小值是( )
A.B.C.D.
10.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②>0;③ac﹣b+1=0;④方程ax2+bx+c=c有两个不相等的实数根.其中正确结论的个数是( )
A.4B.3C.2D.1
二、填空题(本题共6个小题)
11.写出一个经过原点、开口向上且对称轴是直线x=3的抛物线的解析式: .
12.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为 m.
13.5G技术大大促进了农业的发展,某5G智慧农业试验区内,一台无人机正在进行规模化自助施药作业.如图,已知无人机的飞行速度为3m/s,在地面的A点测得B处无人机的仰角为45°,经过4s后,无人机水平飞行至C处,此时在A点测得C处无人机的仰角为30°,则无人机的飞行高度为 m(结果保留根号).
14.如图所示,点B的坐标是(0,),⊙B与x轴相切于点O,交y轴于点C,双曲线y=(x>0)与⊙O的一个交点为A,连接OA,若OA=,则k= .
15.如图所示,边长为1的正方形网格中,O,A,B,C,D是网格线交点,若与所在圆的圆心都为点O,那么阴影部分的面积为 .
16.等腰△ABC中,AB=AC=5,BC=6,AD⊥BC,点O1、O2分别是△ABC的内心和外心,则O1O2= .
三、解答题(本大题共8个小题,要写出必要的解答过程或推理步骤)
17.计算:sin30°﹣|﹣tan60°|+(2024﹣π)0﹣2﹣1﹣.
18.我市某中学举行“中国梦•我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
(1)参加比赛的学生人数共有 名,在扇形统计图中,表示“D等级”的扇形的圆心角为 度,图中m的值为 ;
(2)补全条形统计图;
(3)组委会决定从本次比赛中获得A等级的学生中,选出两名去参加市中学生演讲比赛,已知A等级中男生只有1名,请用画树状图或列表的方法求出所选学生恰是一男一女的概率.
19.(1)尺规作图:已知⊙O及圆外一点P,过点P作圆的两条切线PA,PB,切点分别是点A、点B;(不写作法,保留作图痕迹)
(2)连接AO并延长,交⊙O于点D,连接BD,∠ADB=70°,求∠APB 的度数.
20.如图,正比例函数y=x的图象与反比例函数y=(x>0)的图象交于点A(1,a),在△ABC中,∠ACB=90°,CA=CB,点C坐标为(﹣2,0).
(1)求k的值;
(2)求AB所在直线的解析式.
21.某广场的旗杆AB旁边有一个半圆的时钟模型,如图所示,时钟的9点和3点的刻度线刚好和地面重合,半圆的半径2米,旗杆的底端A到钟面9点刻度C的距离为5米,一天李华同学观察到阳光下旗杆顶端B的影子刚好投到时钟的11点的刻度上,同时测得一米长的标杆的影长1.6米,
(1)计算时钟的9点转到11点时的旋转角是多少度?
(2)求旗杆AB的高度.(精确到0.1米,参考数据≈1.414,≈1.732)
22.某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)如果该文具的销售单价高于进价且不超过30元,请你计算最大利润.
23.如图,在等腰△ABC中,AB=AC.E为BC的中点,BD平分∠ABC交AE于D.经过B,D两点的⊙O交BC于点G.交AB于点F.FB恰为⊙O的直径.
(1)求证:AE与⊙O相切.
(2)当AC=10,csC=时,求⊙O的半径.
24.如图,已知抛物线y=ax2+bx+5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上存在一点P,使PA+PC的值最小,此时P的坐标为 ;
(3)点D是第一象限内抛物线上的一个动点(不与点C、点B重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由;
(4)若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.
参考答案
一、选择题(本题共10个小题,下列每小题均给出四个备选答案,其中只有一个是正确的)。
1.如图,将三棱柱的一个角切割掉,所得几何体的左视图为( )
A.B.C.D.
【分析】根据从左边看得到的图形是左视图,可得答案.
解:从左边看,可得选项B的图形.
故选:B.
【点评】本题考查了简单组合体的三视图,从左边看得到的图形是左视图.
2.若sin(α+20°)=cs50°,则α的度数是( )
A.50°B.40°C.30°D.20°
【分析】互余两角三角函数的关系即可得出答案.
解:∵sin(α+20°)=cs50°,
∴α+20°+50°=90°,
∴α=20°.
故选:D.
【点评】本题考查了互余两角三角函数的关系,在直角三角形中,∠A+∠B=90°时,正余弦之间的关系为:①一个角的正弦值等于这个角的余角的余弦值,即sinA=cs(90°﹣∠A);②一个角的余弦值等于这个角的余角的正弦值,即csA=sin(90°﹣∠A);也可以理解成若∠A+∠B=90°,那么sinA=csB或sinB=csA.
3.若A(2,4)与B(﹣2,a)都是反比例函数y=(k≠0)图象上的点,则a的值是( )
A.4B.﹣4C.2D.﹣2
【分析】反比例函数图象上的点(x,y)的横纵坐标的积是定值k,即xy=k,据此可得a的值.
解:∵A(2,4)与B(﹣2,a)都是反比例函数y=(k≠0)图象上的点,
∴k=2×4=﹣2a,
∴a=﹣4,
故选:B.
【点评】本题考查了反比例函数图象上点的坐标特征,熟知反比例函数y=(k≠0)图象上的点的横纵坐标的积等于定值k是解答此题的关键.
4.如图,在⊙O中,AB是直径,弦AC=5,∠BAC=∠D.则AB的长为( )
A.5B.10C.5D.10
【分析】根据圆周角定理得出∠D=∠B,进而得出△ABC是等腰直角三角形,进而解答即可.
解:∵AC=AC,
∴∠D=∠B,
∵∠BAC=∠D,
∴∠B=∠BAC,
∴△ABC是等腰三角形,
∵AB是直径,
∴△ABC是等腰直角三角形,
∵AC=5,
∴AB=5,
故选:C.
【点评】此题考查圆周角定理,关键是根据圆周角定理得出∠D=∠B解答.
5.二次函数y=ax2+bx+c(a≠0)的图象的顶点坐标是(﹣2,﹣1),且图象与y轴交于点(0,﹣9).将该二次函数的图象以原点为旋转中心旋转180°,则旋转后得到的函数表达式为( )
A.y=﹣2(x+2)2﹣1B.y=﹣2(x+2)2+1
C.y=2(x﹣2)2+1D.y=2(x﹣2)2﹣1
【分析】将二次函数y=ax2+bx+c的图象以原点为旋转中心顺时针旋转180°后,顶点为(2,1),与y轴交于点(0,9),据此可得出所求的结论.
解:将二次函数y=ax2+bx+c的图象以原点为旋转中心顺时针旋转180°,顶点为(2,1),与y轴交于点(0,9),
∴y=a(x﹣2)2+1,
把(0,9)代入得,9=4a+1,
∴a=2,
∴旋转后得到的函数解析式为y=2(x﹣2)2+1,
故选:C.
【点评】本题考查了二次函数图象与几何变换,在绕抛物线顶点旋转过程中,求得二次函数的顶点坐标和与y轴的交点是解题的关键.
6.如图,是某斜坡横断面示意图,为了防止水土流失,将原来的斜坡AC改造成斜坡AB,过点A作水平面的垂线AD,设斜坡AC的坡度为iAC,坡角为∠ACD,斜坡AB的坡度为iAB,坡角为∠ABD,若iAC=2iAB,则下列结论正确的是( )
A.坡度的单位是度B.∠ACD=2∠ABD
C.iAC=D.BD=2CD
【分析】根据坡度的概念判断即可.
解:A、∵坡度是坡面的铅直高度h和水平宽度l的比,
∴坡度没有单位,故本选项结论错误,不符合题意;
B、由题意可知tan∠ACD=2tan∠ABD,
而∠ACD≠2∠ABD,故本选项结论错误,不符合题意;
C、iAC=,故本选项结论错误,不符合题意;
D、∵iAC=2iAB,
∴=2×,
∴BD=2CD,本选项结论正确,符合题意;
故选:D.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,熟记坡度是坡面的铅直高度h和水平宽度l的比是解题的关键.
7.如图,六个直角边长均为1和的直角三角形围成两个正六边形,若向该图形内随意投掷一个点,则该点落在小正六边形内部的概率是( )
A.B.C.D.
【分析】先确定直角三角形斜边长为2,则小正六边形的边长为1,由于正六边形可以化为6个等边三角形,所以小正六边形的面积=6××12=,接着计算出大正六边形的面积,然后小正六边形的面积除以大正六边形的面积即可.
解:∵直角三角形的直角边边长均为1和,
∴直角三角形斜边长为2,
∴小正六边形的边长为2﹣1=1,
∴小正六边形的面积=6××12=,
∴大正六边形的面积=6××1×+=,
∴该点落在小正六边形内部的概率==.
故选:A.
【点评】本题考查了几何概率:某事件的概率=这个事件所占的面积与总面积之比.熟练掌握正六边形的性质是解决问题的关键.
8.如图,已知圆锥的母线与高的夹角为30°,则圆锥侧面展开扇形的圆心角度数为( )
A.90°B.120°C.180°D.210°
【分析】设圆锥底面圆的半径OB=r,求出圆锥的底面圆的周长为2πr,关键含30°角的直角三角形的性质求出BC=2r,设展开后扇形的圆心角的度数为n°,根据弧长公式得出=2πr,求出n即可.
解:设圆锥底面圆的半径OB=r,则圆锥的底面圆的周长为2πr,
∵∠COB=90°,∠OCB=30°,
∴BC=2OB=2r,
设展开后扇形的圆心角的度数为n°,
则=2πr,
解得:n=180,
即圆锥侧面展开扇形的圆心角度数为180°,
故选:C.
【点评】本题考查了圆锥的计算,弧长公式和直角三角形性质等知识点,能根据弧长公式得出=2πr是解此题的关键.
9.⊙O的半径为1,直线l与⊙O相离,点P是直线l上一动点,过点P作⊙O的一条切线PA(其中点A是切点),圆心O到直线l的距离为3,则PA的最小值是( )
A.B.C.D.
【分析】连接OA,由切线的性质得到∠OAP=90°,由勾股定理得到PA==,因此当PO⊥l时,PA最小,由圆心O到直线l的距离为3,得到PO的最小值是3,即可求出PA的最小值是2.
解:连接OA,
∵PA切圆于A,
∴半径OA⊥PA,
∴∠OAP=90°,
∵圆的半径OA=1,
∴PA==,
∴当PO最小时,PA最小,当PO⊥l时,PO最小,
∵圆心O到直线l的距离为3,
∴PO的最小值是3,
∴PA==2,
∴PA的最小值是2.
故选:B.
【点评】本题考查切线的性质,垂线段最短,关键是由勾股定理得到PA==,由此得到当PO⊥l时,PA最小.
10.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②>0;③ac﹣b+1=0;④方程ax2+bx+c=c有两个不相等的实数根.其中正确结论的个数是( )
A.4B.3C.2D.1
【分析】通过抛物线开口方向,对称轴位置及抛物线与x轴交点位置可判断①,由抛物线顶点在x轴上方可判断>0,从而判断②,由OA=OC可得点A坐标为(﹣c,0),进而判断③,抛物线与直线y=c有两个交点可判断④.
解:∵抛物线开口向下,
∴a<0,
∵对称轴在x轴右侧,
∴a,b异号,即b>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc<0,①正确,符合题意.
∵抛物线顶点纵坐标大于0,
∴>0,即<0,②错误,不符合题意.
∵抛物线与x轴有2个交点,
把x=0代入y=ax2+bx+c得y=c,
∴点C坐标为(0,c),OC=c,
∵OA=OC,
∴点A坐标为(﹣c,0),
∴ac2﹣bc+c=0,
∴ac﹣b+1=0,③正确,符合题意.
由图象可知,抛物线与直线y=c有两个交点,
∴方程ax2+bx+c=c有两个不相等的实数根,④正确,符合题意.
故选:B.
【点评】本题考查二次函数图象与系数的关系,解题关键是掌握二次函数图象的性质,掌握二次函数与方程的关系.
二、填空题(本题共6个小题)
11.写出一个经过原点、开口向上且对称轴是直线x=3的抛物线的解析式: y=x2﹣6x(答案不唯一) .
【分析】经过原点则c=0,开口向上则a为正,据此写出一个对称轴是直线x=3的抛物线的解析式即可.
解:经过原点、开口向上且对称轴是直线x=3的抛物线的解析式可以是y=(x﹣3)2﹣9=x2﹣6x;
故答案为:y=x2﹣6x(答案不唯一).
【点评】本题考查求二次函数解析式,解题的关键是掌握二次函数的性质.
12.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为 m.
【分析】利用中心投影的特点得到AB∥OP,则可判断△ABC∽△OPC,然后利用相似比求OP的长.
解:∵AB∥OP,
∴△ABC∽△OPC,
∴=,即=,
∴OP=(m).
故答案为.
【点评】本题考查了中心投影:中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.也考查了相似三角形的判定与性质.
13.5G技术大大促进了农业的发展,某5G智慧农业试验区内,一台无人机正在进行规模化自助施药作业.如图,已知无人机的飞行速度为3m/s,在地面的A点测得B处无人机的仰角为45°,经过4s后,无人机水平飞行至C处,此时在A点测得C处无人机的仰角为30°,则无人机的飞行高度为 (6﹣6) m(结果保留根号).
【分析】过点A作AD⊥BC于点D.由题意可得BC=4×3=12(m),∠DBA=45°,∠ACD=30°,在Rt△ABD中,设AD=x m,则BD=x m,CD=(12﹣x)m,在Rt△ACD中,tan30°=,解方程即可.
解:过点A作AD⊥BC于点D.
由题意可得BC=4×3=12(m),∠DBA=45°,∠ACD=30°,
在Rt△ABD中,设AD=x m,则BD=x m,
∴CD=(12﹣x)m,
在Rt△ACD中,
tan30°=,
解得AD=6﹣6.
∴无人机的飞行高度为(6﹣6)m.
故答案为:(6﹣6).
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
14.如图所示,点B的坐标是(0,),⊙B与x轴相切于点O,交y轴于点C,双曲线y=(x>0)与⊙O的一个交点为A,连接OA,若OA=,则k= 2 .
【分析】作AD⊥x轴于D,BE⊥OA于E,根据垂径定理得出OE=AE==,利用勾股定理求得BE,然后通过证得△BOE∽△OAD,求得OD和AD的长度,即可求得点A的坐标,代入y=(x>0)即可求得k的值.
解:作AD⊥x轴于D,BE⊥OA于E,
∴OE=AE==,
∵点B的坐标是(0,),⊙B与x轴相切于点O,
∴OB=,BO⊥OD,
∴BE===,
∵∠AOD+∠BOE=90°=∠AOD+∠OAD,
∴∠BOE=∠OAD,
∵∠BEO=∠ADO=90°,
∴△BOE∽△OAD,
∴,
∴,
∴OD=2,AD=1,
∴A(2,1),
∵双曲线y=(x>0)与⊙O的一个交点为A,
∴1=,
∴k=2.
故答案为:2.
【点评】本题考查了反比例函数图象上点的坐标特征,切线的性质,垂径定理的应用,勾股定理的应用,三角形相似的判定和性质,求得点A的坐标是解题的关键.
15.如图所示,边长为1的正方形网格中,O,A,B,C,D是网格线交点,若与所在圆的圆心都为点O,那么阴影部分的面积为 π﹣2 .
【分析】根据勾股定理分别求出OC、OD,根据勾股定理的逆定理得到∠COD=90°,根据弧长公式计算,得到答案.
解:由勾股定理得,,
则OC2+OD2=CD2,
∴∠COD=90°,
∵四边形OACB是正方形,
∴∠COB=45°,
∴,,,
∴阴影部分的面积为.
故答案为:.
【点评】本题考查的是扇形面积的计算,掌握扇形面积公式,求出对应的圆心角和半径是解题的关键.
16.等腰△ABC中,AB=AC=5,BC=6,AD⊥BC,点O1、O2分别是△ABC的内心和外心,则O1O2= .
【分析】连接O2B,如图,设△ABC的内切圆的半径为r,外接圆的半径为R,利用等腰三角形的性质得到BD=CD=BC=3,∠ADB=90°,AD平分∠BAC,则根据三角形外心与内心的定义可判断点O1、O2在AD上,
再利用勾股定理计算出AD=4,由于O2A=O2B=R,则O2D=4﹣R,所以利用勾股定理得到(4﹣R)2+32=R2,解方程得R=,则O2D=,接着利用三角形内心的性质得到点O1到△ABC各边的距离都等于r,利用三角形面积公式得到S△ABC=(AB+BC+AC)r=8r,而S△ABC=12,则8r=12,解得r=,即O1D=,然后计算O1D﹣O2D即可.
解:连接O2B,如图,设△ABC的内切圆的半径为r,外接圆的半径为R,
∵AB=AC=5,AD⊥BC,
∴BD=CD=BC=3,∠ADB=90°,AD平分∠BAC,
∴点O1、O2在AD上,
在Rt△ABD中,AD===4,
∵点O2分别是△ABC的外心,
∴O2A=O2B=R,
∴O2D=4﹣R,
在Rt△BDO2中,(4﹣R)2+32=R2,
解得R=,
∴O2D=4﹣=,
∵点O1是△ABC的内心,
∴点O1到△ABC各边的距离都等于r,
∴S△ABC=(AB+BC+AC)r=×(5+6+5)r=8r,
∵S△ABC=BC•AD=×6×4=12,
∴8r=12,
解得r=,
即O1D=,
∴O1O2=O1D﹣O2D=﹣=.
故答案为:.
【点评】本题考查了三角形的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了三角形外接圆与外心、等腰三角形的性质和三角形的面积.
三、解答题(本大题共8个小题,要写出必要的解答过程或推理步骤)
17.计算:sin30°﹣|﹣tan60°|+(2024﹣π)0﹣2﹣1﹣.
【分析】首先计算零指数幂、负整数指数幂、特殊角的三角函数值、开平方和绝对值,然后从左向右依次计算,求出算式的值即可.
解:sin30°﹣|﹣tan60°|+(2024﹣π)0﹣2﹣1﹣
=﹣+1﹣﹣
=﹣+1﹣﹣(1﹣)
=﹣+1﹣﹣1+
=﹣.
【点评】此题主要考查了实数的运算,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.
18.我市某中学举行“中国梦•我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
(1)参加比赛的学生人数共有 20 名,在扇形统计图中,表示“D等级”的扇形的圆心角为 72 度,图中m的值为 40 ;
(2)补全条形统计图;
(3)组委会决定从本次比赛中获得A等级的学生中,选出两名去参加市中学生演讲比赛,已知A等级中男生只有1名,请用画树状图或列表的方法求出所选学生恰是一男一女的概率.
【分析】(1)根据等级为A的人数除以所占的百分比求出总人数,用360°乘以D等级对应比例可得其圆心角度数,根据百分比的概念可得m的值;
(2)求出等级B的人数,补全条形统计图即可;
(3)列表得出所有等可能的情况数,找出符合条件的情况数,即可求出所求的概率.
【解答】(1)解:根据题意得:总人数为:3÷15%=20(人),
表示“D等级”的扇形的圆心角为;
C等级所占的百分比为,
所以m=40,
故答案为:20,72,40.
(2)解:等级B的人数为20﹣(3+8+4)=5(人),
补全统计图,如图所示:
(3)解:根据题意,列出表格,如下:
共有6种等可能结果,其中恰是一男一女的有4种,
所以恰是一男一女的概率为.
【点评】此题考查了条形统计图,扇形统计图以及列表法与树状图法,弄清题意,从条形图和扇形图得到解题所需数据是解本题的关键.
19.(1)尺规作图:已知⊙O及圆外一点P,过点P作圆的两条切线PA,PB,切点分别是点A、点B;(不写作法,保留作图痕迹)
(2)连接AO并延长,交⊙O于点D,连接BD,∠ADB=70°,求∠APB 的度数.
【分析】(1)连接OP,作线段OP的垂直平分线,交OP于点M,再以点M为圆心,PM的长为半径画圆,分别交⊙O于点A,B,连接PA,PB即可.
(2)连接OA,OB,由切线的性质可得OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,由圆周角定理得到∠AOB=2∠ACD=140°,根据四边形内角和为360°即可得的答案.
解:(1)如图,连接OP,作线段OP的垂直平分线,交OP于点M,
再以点M为圆心,PM的长为半径画圆,分别交⊙O于点A,B,连接PA,PB.
由圆周角定理可得,∠OAP=∠OBP=90°,
∵OA,OB为⊙O的半径,
∴PA,PB为⊙O的切线.
则PA,PB即为所求;
(2)连接OB,
∵PA,PB为⊙O的两条切线,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠ADB=70°,
∴∠AOB=2∠ACD=140°,
∴∠APB=360°﹣∠OAP﹣∠OBP﹣∠AOB=40°.
【点评】本题考查作图—复杂作图、圆周角定理、切线的判定与性质,熟练掌握圆周角定理、切线的判定与性质是解答本题的关键.
20.如图,正比例函数y=x的图象与反比例函数y=(x>0)的图象交于点A(1,a),在△ABC中,∠ACB=90°,CA=CB,点C坐标为(﹣2,0).
(1)求k的值;
(2)求AB所在直线的解析式.
【分析】(1)先求得A的坐标,然后根据待定系数法即可求得k的值;
(2)作AD⊥x轴于点D,BE⊥x轴于点E,通过证得△BCE≌△CAD,求得B(﹣3,3),然后根据待定系数法即可求得直线AB的解析式.
解:(1)∵正比例函数y=x的图象经过点A(1,a),
∴a=1,
∴A(1,1),
∵点A在反比例函数y=(x>0)的图象上,
∴k=1×1=1;
(2)作AD⊥x轴于点D,BE⊥x轴于点E,
∵A(1,1),C(﹣2,0),
∴AD=1,CD=3,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵∠ACD+∠CAD=90°,
∴∠BCE=∠CAD,
在△BCE和△CAD中,
,
∴△BCE≌△CAD(AAS),
∴CE=AD=1,BE=CD=3,
∴B(﹣3,3),
设直线AB的解析式为y=mx+n,
∴,解得,
∴直线AB的解析式为y=﹣+.
【点评】本题是反比例函数与一次函数的交点问题,考查了一次函数图象上点的坐标特征,待定系数法求一次函数的解析式,全等三角形的判定和性质,求得B的坐标是解题的关键.
21.某广场的旗杆AB旁边有一个半圆的时钟模型,如图所示,时钟的9点和3点的刻度线刚好和地面重合,半圆的半径2米,旗杆的底端A到钟面9点刻度C的距离为5米,一天李华同学观察到阳光下旗杆顶端B的影子刚好投到时钟的11点的刻度上,同时测得一米长的标杆的影长1.6米,
(1)计算时钟的9点转到11点时的旋转角是多少度?
(2)求旗杆AB的高度.(精确到0.1米,参考数据≈1.414,≈1.732)
【分析】(1)根据钟表的一个大格是30°,从9点转到11点时针转过2个大格,列式计算即可得解.
(2)过点D作DE⊥AC于E,作DF⊥AB于F,设半圆圆心为O,连接OD,解直角三角形求出DE,OE,然后求出DF,再根据同时同地的物高与影长成比例列式求出DF,然后根据AB=AF+DE计算即可得解.
解:(1)从时钟的9点转到11点时时针转过2个大格,
所以,2×30°=60°;
(2)如图,过点D作DE⊥AC于E,作DF⊥AB于F,设半圆圆心为O,连接OD,
∵点D在11点的刻度上,
∴∠COD=60°,
∴DE=OD•sin60°=2×=,
OE=OD•cs60°=2×=1,
∴CE=2﹣1=1,
∴DF=AE=5+1=6,
∵同时测得一米长的标杆的影长1.6米,
∴=,
∴BF==,
∴AB=BF+DE=(+)≈5.5(米).
答:旗杆AB的高度约为5.5米.
【点评】本题考查了相似三角形的应用,解直角三角形,作辅助线构造出直角三角形和矩形是解题的关键.
22.某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)如果该文具的销售单价高于进价且不超过30元,请你计算最大利润.
【分析】(1)根据利润=(单价﹣进价)×销售量,列出函数关系式即可;
(2)根据(1)式列出的函数关系式,运用配方法求最大值;
(3)利用二次函数增减性直接求出最值即可.
解:(1)由题意得,销售量=250﹣10(x﹣25)=﹣10x+500,
则w=(x﹣20)(﹣10x+500)
=﹣10x2+700x﹣10000;
(2)w=﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250.
∵﹣10<0,
∴函数图象开口向下,w有最大值,
当x=35时,wmax=2250,
故当单价为35元时,该文具每天的利润最大;
(3)20<x≤30,对称轴左侧w随x的增大而增大,
故当x=30时,w有最大值,此时w=2000.
【点评】本题考查了二次函数的应用,难度较大,最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=﹣时取得.
23.如图,在等腰△ABC中,AB=AC.E为BC的中点,BD平分∠ABC交AE于D.经过B,D两点的⊙O交BC于点G.交AB于点F.FB恰为⊙O的直径.
(1)求证:AE与⊙O相切.
(2)当AC=10,csC=时,求⊙O的半径.
【分析】(1)连接OD,可得∠ODB=∠OBD=∠DBE,进而推出OD∥BE,由平行线的性质得到∠ADO=∠AEB,由等腰三角形的性质得到AE⊥BC,得到∠AMO=∠AEB=90°,由圆的切线的判定即可证得结论;
(2)首先证得△AOD∽△ABE,根据相似三角形对应边成比例即可求解.
【解答】(1)证明:连接OD,则OD=OB,
∴∠OBD=∠OMB,
∵BD平分∠ABC,
∴∠OBD=∠EBD,
∴∠ODB=∠EBD,
∴OD∥BE,
∴∠ADO=∠AEB,
在△ABC中,AB=AC,AE是角平分线,
∴AE⊥BC,
∴∠ADO=∠AEB=90°,
∵OD是⊙O的半径,
∴AE与⊙O相切;
(2)解:在△ABC中,AB=AC=10,E为BC的中点,
∴BE=BC,
∴在Rt△ABE中,csC===,
∴BE=6,
设⊙O的半径为r,则AO=10﹣r,
∵OD∥BC,
∴△AOD∽△ABE,
∴=,
即=,
∴r=,
即⊙O的半径为.
【点评】本题考查了切线的性质和判定,等腰三角形的性质,平行线的性质和判定,相似三角形的判定与性质,解题的关键是正确作出辅助线进行证明.
24.如图,已知抛物线y=ax2+bx+5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上存在一点P,使PA+PC的值最小,此时P的坐标为 (2,3) ;
(3)点D是第一象限内抛物线上的一个动点(不与点C、点B重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由;
(4)若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.
【分析】(1)用待定系数法即可求解;
(2)点A关于抛物线对称轴的对称点为点B,则BC交抛物线对称轴于点P,点P为所求点,即可求解;
(3)当直线BC能否把△BDF分成面积之比为2:3的两部分时,即EF=或DF,即可求解;
(4)当BC是斜边时,由勾股定理列出等式,即可求解;当MB或MC为斜边时,同理可解.
解:(1)设抛物线的表达式为:y=a(x+1)(x﹣5)=a(x2﹣4x﹣5),
则﹣5a=5,
解得:a=﹣1,
则抛物线的表达式为:y=﹣x2+4x+5;
(2)由(1)知,抛物线的对称轴为直线x=2,
点A关于抛物线对称轴的对称点为点B,则BC交抛物线对称轴于点P,点P为所求点,理由:
PA+PC=PB+PC=BC为最小,
由点B、C(0,5)的坐标得,直线BC的表达式为:y=﹣x+5,
当x=2时,y=3,
即点P(2,3),
故答案为:(2,3);
(3)能,理由:
当直线BC能否把△BDF分成面积之比为2:3的两部分时,即EF=或DF,
设点D(m,﹣m2+4m+5),点E(m,﹣m+5),
则﹣m+5=(﹣m2+4m+5)或﹣m+5=(﹣m2+4m+5),
解得:m=或,
则点D(,)或(,);
(4)设点M(2,m),
由点M、B、C的坐标得,BC2=50,BM2=9+m2,CM2=4+(m﹣5)2,
当BC是斜边时,
则50=9+m2+4+(m﹣5)2,
解得:m=6或﹣1,
即点M(2,6)或(2,﹣1);
当MB或MC为斜边时,同理可得:
9+m2=4+(m﹣5)2+50或4+(m﹣5)2=50+9+m2,
解得:m=7或﹣3,
即点M(2,7)或(2,﹣3),
综上,点M的坐标为:(2,6)或(2,﹣1)或(2,7)或(2,﹣3).
【点评】本题考查的是二次函数的综合运用,涉及到面积的计算,直角三角形的性质、点的对称性等,分类求解是解题的关键.
男
女1
女2
男
女1、男
女2、男
女1
男、女1
女2、女1
女2
男、女2
女1、女2
相关试卷
这是一份山东省烟台市莱州市2023-2024学年七年级上学期1月期末数学试题+,共13页。试卷主要包含了下列说法中,正确的是等内容,欢迎下载使用。
这是一份山东省烟台市莱州市2023-2024学年八年级上学期1月期末数学试题,共3页。
这是一份山东省烟台市莱州市2023-2024学年九年级上学期期中数学试题,共14页。试卷主要包含了如图,在中,,等内容,欢迎下载使用。









