2023-2024学年河南省驻马店市平舆一中九年级（上）期末数学试卷(含解析)

这是一份2023-2024学年河南省驻马店市平舆一中九年级（上）期末数学试卷(含解析)，共22页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
1．已知⊙O是以坐标原点O为圆心，5为半径的圆，点M的坐标为（﹣3，4），则点M与⊙O的位置关系为（ ）
A．M在⊙O上B．M在⊙O内
C．M在⊙O外D．M在⊙O右上方
2．如图，点A，B，C是⊙O上的三点，已知∠AOB＝100°，那么∠ACB的度数是（ ）
A．30°B．40°C．50°D．60°
3．下列函数中，属于二次函数的是（ ）
A．y＝2x+1B．y＝（x﹣1）2﹣x2
C．y＝2x2﹣7D．
4．若x＝a是方程x2﹣x﹣2016＝0的根，则代数式2a2﹣2a﹣2016的值为（ ）
A．1B．2016C．﹣1D．﹣2016
5．如图，在平行四边形ABCD中，点E是边AD上一点，且AE＝2ED，EC交对角线BD于点F，则＝（ ）
A．B．C．D．
6．把二次函数y＝x2﹣4x+1化成y＝a（x﹣m）2+k的形式是（ ）
A．y＝（x﹣2）2+1B．y＝（x﹣2）2﹣1
C．y＝（x﹣2）2+3D．y＝（x﹣2）2﹣3
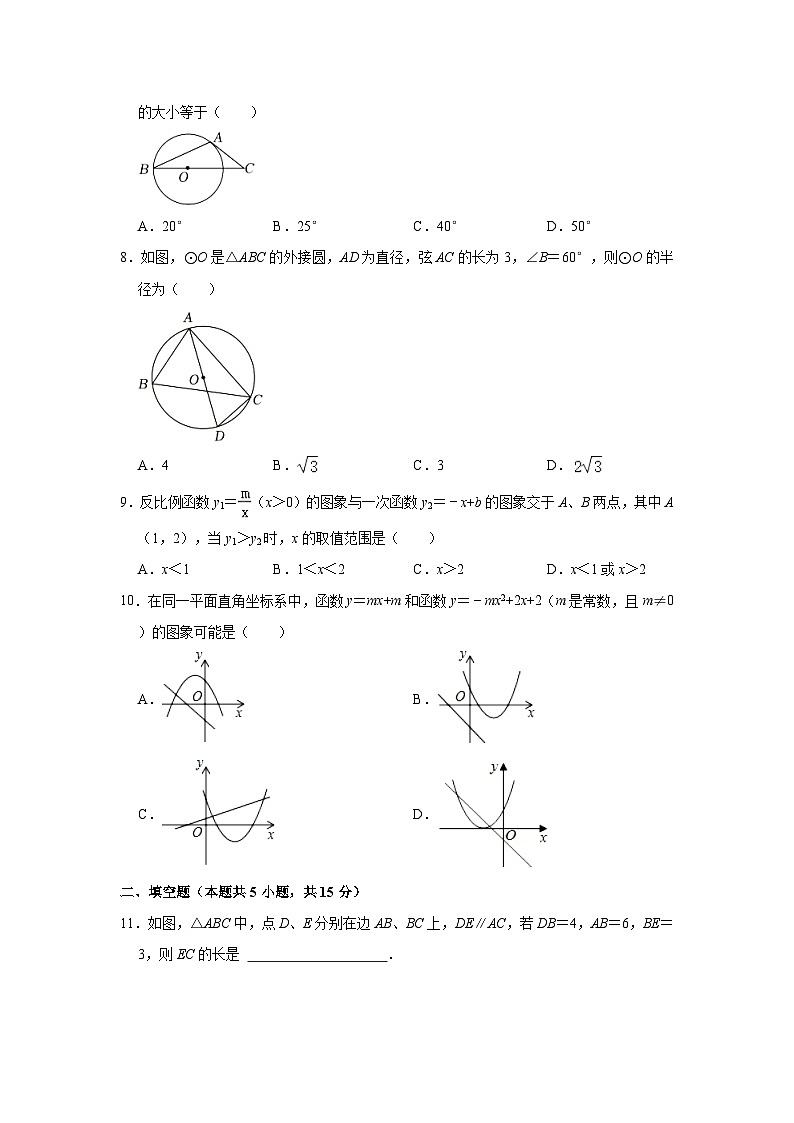
7．如图，AB是⊙O的弦，AC是⊙O切线，A为切点，BC经过圆心．若∠B＝20°，则∠C的大小等于（ ）
A．20°B．25°C．40°D．50°
8．如图，⊙O是△ABC的外接圆，AD为直径，弦AC的长为3，∠B＝60°，则⊙O的半径为（ ）
A．4B．C．3D．
9．反比例函数y1＝（x＞0）的图象与一次函数y2＝﹣x+b的图象交于A、B两点，其中A（1，2），当y1＞y2时，x的取值范围是（ ）
A．x＜1B．1＜x＜2C．x＞2D．x＜1或x＞2
10．在同一平面直角坐标系中，函数y＝mx+m和函数y＝﹣mx2+2x+2（m是常数，且m≠0）的图象可能是（ ）
A．B．
C．D．
二、填空题（本题共5小题，共15分）
11．如图，△ABC中，点D、E分别在边AB、BC上，DE∥AC，若DB＝4，AB＝6，BE＝3，则EC的长是 ．
12．已知关于x的一元二次方程x2+2x+m＝0有实数根，则m的取值范围是 ．
13．在反比例函数y＝﹣的图象上有（x1，y1），（x2，y2），（x3，y3）三点，若x1＞x2＞0＞x3，则y1，y2，y3的大小关系是 ．
14．如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝8，AE＝1，则弦CD的长是 ．
15．如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：
①4ac＜b2；
②方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3；
③3a+c＞0；
④当y＞0时，x的取值范围是﹣1≤x＜3；
⑤当x＜0时，y随x增大而增大；
其中结论正确有 ．
三．解答题（共75分）
16．解方程：
（1）x2+2x＝0；
（2）2x2﹣4x﹣1＝0．
17．如图，某公园的人工湖边上有一座假山，假山顶上有一座高为5米的建筑物CD，数学小组为了测量假山DE的高度，在公园找了一水平地面，在A处测得建筑物底部D点（即假山顶）的仰角为30°，沿水平方向前进25米到达B点，测得建筑物顶部C点的仰角为45°，点A，B，C，D，E在同一平面内，求假山DE的高度．（结果保留根号）
18．如图，已知反比例函数的图象与一次函数的图象交于A和B（8，n）两点．
（1）求k和n的值；
（2）若点C（x，y）也在反比例函数的图象上，求当2≤x≤8时，函数值y的取值范围．
19．如图，△ABC中，PC平分∠ACB，PB＝PC．
（1）求证：△APC∽△ACB；
（2）若AP＝2，PC＝6，求AC的长．
20．已知关于x的方程x2﹣（k+2）x+2k＝0．
（1）求证：无论k取任意实数值，方程总有实数根．
（2）若等腰三角形ABC的一边a＝1，另两边长b、c恰是这个方程的两个根，求△ABC的周长．
21．如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC＝CB，延长DA与⊙O的另一个交点为E，连接AC，CE．
（1）求证：∠B＝∠D；
（2）若AB＝4，BC﹣AC＝2，求CE的长．
22．如图，点A（3，5）关于原点O的对称点为点C，分别过点A，C作y轴的平行线，与反比例函数y＝（0＜k＜15）的图象交于点B，D，连接AD，BC，AD与x轴交于点E（﹣2，0）．
（1）求k的值；
（2）直接写出阴影部分面积之和．
23．如图，在Rt△ABC中，AB＝3，AC＝4，∠BAC＝90°，AD⊥BC于点D，O为AC的中点，连接BO交AD于点F，OE⊥OB交BC于点E，求OF：OE的值．
参考答案
一、选择题（本题共10小题，共30分）
1．已知⊙O是以坐标原点O为圆心，5为半径的圆，点M的坐标为（﹣3，4），则点M与⊙O的位置关系为（ ）
A．M在⊙O上B．M在⊙O内
C．M在⊙O外D．M在⊙O右上方
【分析】根据勾股定理，可得OM的长，根据点与圆心的距离d，则d＞r时，点在圆外；当d＝r时，点在圆上；当d＜r时，点在圆内．
解：OM＝＝5，
OM＝r＝5．
故选：A．
【点评】本题考查了对点与圆的位置关系的判断．关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d＝r时，点在圆上，当d＜r时，点在圆内．
2．如图，点A，B，C是⊙O上的三点，已知∠AOB＝100°，那么∠ACB的度数是（ ）
A．30°B．40°C．50°D．60°
【分析】根据图形，利用圆周角定理求出所求角度数即可．
解：∵∠AOB与∠ACB都对，且∠AOB＝100°，
∴∠ACB＝∠AOB＝50°，
故选：C．
【点评】此题考查了圆周角定理，熟练掌握圆周角定理是解本题的关键．
3．下列函数中，属于二次函数的是（ ）
A．y＝2x+1B．y＝（x﹣1）2﹣x2
C．y＝2x2﹣7D．
【分析】根据一次函数、反比例函数、二次函数的定义判断各选项即可得出答案．
解：A、是一次函数，故本选项错误；
B、整理后是一次函数，故本选项错误；
C、y＝2x2﹣7是二次函数，故本选项正确；
D、y与x2是反比例函数关系，故本选项错误．
故选：C．
【点评】本题考查了二次函数的定义，关键是掌握二次函数的定义条件：二次函数y＝ax2+bx+c的定义条件是：a、b、c为常数，a≠0，自变量最高次数为2．
4．若x＝a是方程x2﹣x﹣2016＝0的根，则代数式2a2﹣2a﹣2016的值为（ ）
A．1B．2016C．﹣1D．﹣2016
【分析】根据题意可得：把x＝a代入方程x2﹣x﹣2016＝0中得：a2﹣a﹣2016＝0，从而可得a2﹣a＝2016，然后代入式子中进行计算，即可解答．
解：由题意得：把x＝a代入方程x2﹣x﹣2016＝0中得：
a2﹣a﹣2016＝0，
∴a2﹣a＝2016，
∴2a2﹣2a﹣2016＝2（a2﹣a）﹣2016
＝2×2016﹣2016
＝4032﹣2016
＝2016，
故选：B．
【点评】本题考查了一元二次方程的解，准确熟练地进行计算是解题的关键．
5．如图，在平行四边形ABCD中，点E是边AD上一点，且AE＝2ED，EC交对角线BD于点F，则＝（ ）
A．B．C．D．
【分析】由平行四边形对边平行且相等得到AD与BC平行且相等，由平行得到两对内错角相等，由两对角相等的三角形相似得到三角形EDF与三角形CBF相似，由相似得比例即可求出所求式子的值．
解：∵平行四边形ABCD，
∴AD∥BC，AD＝BC，
∴∠DEF＝∠BCF，∠EDF＝∠CBF，
∴△EDF∽△CBF，
∴＝，
∵AE＝2ED，
∴＝＝，
则＝，
故选：A．
【点评】此题考查了相似三角形的判定与性质，以及平行四边形的性质，熟练掌握相似三角形的判定与性质是解本题的关键．
6．把二次函数y＝x2﹣4x+1化成y＝a（x﹣m）2+k的形式是（ ）
A．y＝（x﹣2）2+1B．y＝（x﹣2）2﹣1
C．y＝（x﹣2）2+3D．y＝（x﹣2）2﹣3
【分析】运用配方法把二次函数的一般式化为顶点式即可．
解：y＝x2﹣4x+1
＝x2﹣4x+4﹣3
＝（x﹣2）2﹣3，
故选：D．
【点评】本题考查的是二次函数的三种形式，正确运用配方法把二次函数的一般式化为顶点式是解题的关键．
7．如图，AB是⊙O的弦，AC是⊙O切线，A为切点，BC经过圆心．若∠B＝20°，则∠C的大小等于（ ）
A．20°B．25°C．40°D．50°
【分析】连接OA，根据切线的性质，即可求得∠C的度数．
解：如图，连接OA，
∵AC是⊙O的切线，
∴∠OAC＝90°，
∵OA＝OB，
∴∠B＝∠OAB＝20°，
∴∠AOC＝40°，
∴∠C＝50°．
故选：D．
【点评】本题考查了圆的切线性质，以及等腰三角形的性质，掌握已知切线时常用的辅助线是连接圆心与切点是解题的关键．
8．如图，⊙O是△ABC的外接圆，AD为直径，弦AC的长为3，∠B＝60°，则⊙O的半径为（ ）
A．4B．C．3D．
【分析】根据圆周角定理得到∠D＝∠B＝60°，∠ACD＝90°，根据正弦的定义计算，得到答案．
解：∵∠B＝60°，
∴∠D＝∠B＝60°，
∵AD为⊙O直径，
∴∠ACD＝90°，
∴AD＝＝＝2，
∴⊙O的半径为，
故选：B．
【点评】本题考查的是圆周角定理、正弦的定义，熟记圆周角定理是解题的关键．
9．反比例函数y1＝（x＞0）的图象与一次函数y2＝﹣x+b的图象交于A、B两点，其中A（1，2），当y1＞y2时，x的取值范围是（ ）
A．x＜1B．1＜x＜2C．x＞2D．x＜1或x＞2
【分析】先求出两个函数解析式，再画出图象，即可得到答案．
解：∵反比例函数y1＝（x＞0）的图象与一次函数y2＝﹣x+b的图象交于A、B两点，其中A（1，2），
∴m＝2，b＝3，
∴反比例函数解析式为：y＝；一次函数解析式为：y＝﹣x+3，
如图：
由图象可知，当y1＞y2时，x的取值范围是0＜x＜1或x＞2．
故选：D．
【点评】本题考查了反比例函数与一次函数的交点问题，交点坐标满足两个函数解析式．
10．在同一平面直角坐标系中，函数y＝mx+m和函数y＝﹣mx2+2x+2（m是常数，且m≠0）的图象可能是（ ）
A．B．
C．D．
【分析】分m＞0及m＜0两种情况考虑两函数的图象，对照四个选项即可得出结论．
解：当m＞0时，函数y＝mx+m的图象经过第一、二、三象限，函数y＝﹣mx2+2x+2的图象开口向下，
∴C选项不符合题意；
当m＜0时，﹣＝＜0，
∴函数y＝mx+m的图象经过第二、三、四象限，函数y＝﹣mx2+2x+2的图象开口向上，且对称轴在y轴左侧，D选项符合题意．
故选：D．
【点评】本题考查了二次函数的图象以及一次函数的图象，分m＞0及m＜0两种情况考虑两函数的图象是解题的关键．
二、填空题（本题共5小题，共15分）
11．如图，△ABC中，点D、E分别在边AB、BC上，DE∥AC，若DB＝4，AB＝6，BE＝3，则EC的长是 ．
【分析】由△ABC中，点D、E分别在边AB、BC上，DE∥AC，根据平行线分线段成比例定理，可得DB：AB＝BE：BC，又由DB＝4，AB＝6，BE＝3，即可求得答案．
解：∵DE∥AC，
∴DB：AB＝BE：BC，
∵DB＝4，AB＝6，BE＝3，
∴4：6＝3：BC，
解得：BC＝，
∴EC＝BC﹣BE＝﹣3＝．
故答案为：．
【点评】此题考查了平行线分线段成比例定理，解题时注意：平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．
12．已知关于x的一元二次方程x2+2x+m＝0有实数根，则m的取值范围是 m≤1 ．
【分析】先根据一元二次方程x2+2x+m＝0得出a、b、c的值，再根据方程有实数根列出关于m的不等式，求出m的取值范围即可．
解：由一元二次方程x2+2x+m＝0可知a＝1，b＝2，c＝m，
∵方程有实数根，
∴Δ＝22﹣4m≥0，解得m≤1．
故答案为：m≤1．
【点评】本题考查的是一元二次方程根的判别式，根据题意列出关于m的不等式是解答此题的关键．
13．在反比例函数y＝﹣的图象上有（x1，y1），（x2，y2），（x3，y3）三点，若x1＞x2＞0＞x3，则y1，y2，y3的大小关系是 y2＜y1＜y3 ．
【分析】由反比例函数y＝﹣的可知，k＝﹣1＜0，函数的图象在二四象限，y随x的增大而增大，由此进行判断．
解：由反比例函数y＝﹣的可知，k＝﹣1＜0，当x＞0时，y随x的增大而增大，
∴当x1＞x2＞0时，则0＞y1＞y2，
又C（x3，y3）在第二象限，y3＞0，
∴y2＜y1＜y3，
故答案为y2＜y1＜y3．
【点评】本题考查了反比例函数图象上点的坐标特点．关键是根据反比例函数的增减性解题．
14．如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝8，AE＝1，则弦CD的长是 2 ．
【分析】根据垂径定理和勾股定理，即可得答案．
解：连接OC，
由题意，得
OE＝OA﹣AE＝4﹣1＝3，
CE＝ED＝＝，
CD＝2CE＝2，
故答案为2．
【点评】本题考查了垂径定理，利用勾股定理，解题关键是学会添加常用辅助线面构造直角三角形解决问题．
15．如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：
①4ac＜b2；
②方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3；
③3a+c＞0；
④当y＞0时，x的取值范围是﹣1≤x＜3；
⑤当x＜0时，y随x增大而增大；
其中结论正确有 ①②⑤ ．
【分析】利用抛物线与x轴的交点个数可对①进行判断；利用抛物线的对称性得到抛物线与x轴的一个交点坐标为（3，0），则可对②进行判断；由对称轴方程得到b＝﹣2a，然后根据x＝﹣1时函数值为0可得到3a+c＝0，则可对③进行判断；根据抛物线在x轴上方所对应的自变量的范围可对④进行判断；根据二次函数的性质对⑤进行判断．
解：∵抛物线与x轴有2个交点，
∴b2﹣4ac＞0，所以①正确；
∵抛物线的对称轴为直线x＝1，
而点（﹣1，0）关于直线x＝1的对称点的坐标为（3，0），
∴方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3，所以②正确；
∵x＝﹣＝1，即b＝﹣2a，
而x＝﹣1时，y＝0，即a﹣b+c＝0，
∴a+2a+c＝0，所以③错误；
∵抛物线与x轴的两点坐标为（﹣1，0），（3，0），
∴当﹣1＜x＜3时，y＞0，所以④错误；
∵抛物线的对称轴为直线x＝1，
∴当x＜1时，y随x增大而增大，所以⑤正确．
故答案为①②⑤．
【点评】本题考查了二次函数图象与系数的关系：对于二次函数y＝ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右；常数项c决定抛物线与y轴交点位置：抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定：Δ＝b2﹣4ac＞0时，抛物线与x轴有2个交点；Δ＝b2﹣4ac＝0时，抛物线与x轴有1个交点；Δ＝b2﹣4ac＜0时，抛物线与x轴没有交点．
三．解答题（共75分）
16．解方程：
（1）x2+2x＝0；
（2）2x2﹣4x﹣1＝0．
【分析】（1）利用因式分解法求解即可；
（2）方程二次项系数化为1变形后，利用配方法求出解即可．
解：（1）∵x2+2x＝0，
∴x（x+2）＝0，
∴x＝0或x+2＝0，
解得：x1＝0，x2＝﹣2；
（2）方程整理得：x2﹣2x＝，
配方得：x2﹣2x+1＝+1，即（x﹣1）2＝，
开方得：x﹣1＝±，
解得：x1＝1+，x2＝1﹣．
【点评】本题考查了一元二次方程的解法，常用的方法有直接开平方法、配方法、因式分解法、求根公式法，熟练掌握各种方法是解答本题的关键．
17．如图，某公园的人工湖边上有一座假山，假山顶上有一座高为5米的建筑物CD，数学小组为了测量假山DE的高度，在公园找了一水平地面，在A处测得建筑物底部D点（即假山顶）的仰角为30°，沿水平方向前进25米到达B点，测得建筑物顶部C点的仰角为45°，点A，B，C，D，E在同一平面内，求假山DE的高度．（结果保留根号）
【分析】解：设假山DE的高度为x，于是得到CE＝DE+CD＝x+5，解直角三角形即可得到结论．
解：设假山DE的高度为x，
则CE＝DE+CD＝x+5，
在Rt△BCE中，
∵∠CBE＝45°，
∴BE＝CE＝x+5，
∴AE＝AB+BE＝30+x，
在Rt△ADE中，∵∠DAE＝30°，DE＝x，
∴AE＝＝x，
解答：x＝15+15，
答：假山DE的高度为（15+15）米．
【点评】此题是解直角三角形的应用﹣﹣﹣仰角和俯角，解本题的关键是利用三角函数解答．
18．如图，已知反比例函数的图象与一次函数的图象交于A和B（8，n）两点．
（1）求k和n的值；
（2）若点C（x，y）也在反比例函数的图象上，求当2≤x≤8时，函数值y的取值范围．
【分析】（1）利用一次函数图象上点的坐标特征可求出n值，进而可得出点B的坐标，再利用反比例函数图象上点的坐标特征即可求出k值；
（2）由k＝8＞0结合反比例函数的性质，可得当x＞0时，y随x值增大而减小，即可求解．
解：（1）把B（8，n）代入，得：，
∴B（8，1），
∵反比例函数过点B（8，1），
∴k＝8×1＝8；
（2）由（1）可知反比例函数的解析式为，
∵k＝8＞0，
∴对于反比例函数，当x＞0时，y随x值增大而减小，
当x＝2时，y＝4，
当x＝8时，y＝1，
∴当2≤x≤8时，1≤y≤4．
【点评】本题考查了反比例函数与一次函数的交点问题，反比例函数的性质，用到了点在函数图象上，则点的坐标就适合所在函数图象的函数解析式，待定系数法等知识，熟练掌握相关知识是解题的关键．
19．如图，△ABC中，PC平分∠ACB，PB＝PC．
（1）求证：△APC∽△ACB；
（2）若AP＝2，PC＝6，求AC的长．
【分析】（1）证明∠B＝∠ACP，结合∠A＝∠A，即可解决问题．
（2）由△APC∽△ACB，得到，利用AP＝2，PC＝6，AB＝8，即可解决问题．
解：（1）∵PB＝PC，
∴∠B＝∠PCB；
∵PC平分∠ACB，
∴∠ACP＝∠PCB，∠B＝∠ACP，
∵∠A＝∠A，
∴△APC∽△ACB．
（2）∵△APC∽△ACB，
∴，
∵AP＝2，PC＝6，AB＝8，
∴AC＝4．
∵AP+AC＝PC＝6，
这与三角形的任意两边之和大于第三边相矛盾，
∴该题无解．
【点评】该题主要考查了相似三角形的判定及其性质的应用问题；牢固掌握相似三角形的判定及其性质是灵活运用、解题的基础和关键．
20．已知关于x的方程x2﹣（k+2）x+2k＝0．
（1）求证：无论k取任意实数值，方程总有实数根．
（2）若等腰三角形ABC的一边a＝1，另两边长b、c恰是这个方程的两个根，求△ABC的周长．
【分析】（1）把一元二次方程根的判别式转化成完全平方式的形式，得出△≥0可知方程总有实数根．
（2）根据等腰三角形的性质分情况讨论求出b，c的长，并根据三角形三边关系检验，综合后求出△ABC的周长．
【解答】证明：（1）∵Δ＝b2﹣4ac＝（k+2）2﹣8k＝（k﹣2）2≥0，
∴无论k取任意实数值，方程总有实数根．
解：（2）分两种情况：
①若b＝c，
∵方程x2﹣（k+2）x+2k＝0有两个相等的实数根，
∴Δ＝b2﹣4ac＝（k﹣2）2＝0，
解得k＝2，
∴此时方程为x2﹣4x+4＝0，解得x1＝x2＝2，
∴△ABC的周长为5；
②若b≠c，则b＝a＝1或c＝a＝1，即方程有一根为1，
∵把x＝1代入方程x2﹣（k+2）x+2k＝0，得1﹣（k+2）+2k＝0，
解得k＝1，
∴此时方程为x2﹣3x+2＝0，
解得x1＝1，x2＝2，
∴方程另一根为2，
∵1、1、2不能构成三角形，
∴所求△ABC的周长为5．
综上所述，所求△ABC的周长为5．
【点评】考查根的判别式，等腰三角形的性质及三角形三边关系．
21．如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC＝CB，延长DA与⊙O的另一个交点为E，连接AC，CE．
（1）求证：∠B＝∠D；
（2）若AB＝4，BC﹣AC＝2，求CE的长．
【分析】（1）由AB为⊙O的直径，易证得AC⊥BD，又由DC＝CB，根据线段垂直平分线的性质，可证得AD＝AB，即可得：∠B＝∠D；
（2）首先设BC＝x，则AC＝x﹣2，由在Rt△ABC中，AC2+BC2＝AB2，可得方程：（x﹣2）2+x2＝42，解此方程即可求得CB的长，继而求得CE的长．
【解答】（1）证明：∵AB为⊙O的直径，
∴∠ACB＝90°，
∴AC⊥BC，
又∵DC＝CB，
∴AD＝AB，
∴∠B＝∠D；
（2）解：设BC＝x，则AC＝x﹣2，
在Rt△ABC中，AC2+BC2＝AB2，
∴（x﹣2）2+x2＝42，
解得：x1＝1+，x2＝1﹣（舍去），
∵∠B＝∠E，∠B＝∠D，
∴∠D＝∠E，
∴CD＝CE，
∵CD＝CB，
∴CE＝CB＝1+．
【点评】此题考查了圆周角定理、线段垂直平分线的性质、等腰三角形的判定与性质以及勾股定理等知识．此题难度适中，注意掌握方程思想与数形结合思想的应用．
22．如图，点A（3，5）关于原点O的对称点为点C，分别过点A，C作y轴的平行线，与反比例函数y＝（0＜k＜15）的图象交于点B，D，连接AD，BC，AD与x轴交于点E（﹣2，0）．
（1）求k的值；
（2）直接写出阴影部分面积之和．
【分析】（1）根据点A和点E的坐标求得直线AE的解析式，然后设出点D的纵坐标，代入直线AE的解析式即可求得点D的坐标，从而求得k值；
（2）根据中心对称的性质得到阴影部分的面积等于平行四边形CDGF的面积即可．
解：（1）∵A（3，5）、E（﹣2，0），
∴设直线AE的解析式为y＝kx+b，
则，
解得：，
∴直线AE的解析式为y＝x+2，
∵点A（3，5）关于原点O的对称点为点C，
∴点C的坐标为（﹣3，﹣5），
∵CD∥y轴，
∴设点D的坐标为（﹣3，a），
∴a＝﹣3+2＝﹣1，
∴点D的坐标为（﹣3，﹣1），
∵反比例函数y＝（0＜k＜15）的图象经过点D，
∴k＝﹣3×（﹣1）＝3；
（2）如图：
∵点A和点C关于原点对称，
∴阴影部分的面积等于平行四边形CDGF的面积，
∴S阴影＝4×3＝12．
【点评】本题考查了反比例函数与一次函数的交点问题，解题的关键是能够确定点D的坐标，难度不大．
23．如图，在Rt△ABC中，AB＝3，AC＝4，∠BAC＝90°，AD⊥BC于点D，O为AC的中点，连接BO交AD于点F，OE⊥OB交BC于点E，求OF：OE的值．
【分析】先证明∠BAF＝∠C，∠ABF＝∠COE，作OH⊥AC，交BC于H，根据相似三角形的性质得到，由三角形中位线定理可得OH＝AB，OA＝OC＝AC，即可求解．
解：∵AD⊥BC，
∴∠DAC+∠C＝90°．
∵∠BAC＝90°，
∴∠BAF＝∠C．
∵OE⊥OB，
∴∠BOA+∠COE＝90°，
∵∠BOA+∠ABF＝90°，
∴∠ABF＝∠COE．
过O作AC的垂线交BC于H，则OH∥AB，
∵∠ABF＝∠COE，∠BAF＝∠C．
∴∠AFB＝∠OEC，
∴∠AFO＝∠HEO，
而∠BAF＝∠C，
∴∠FAO＝∠EHO，
∴△OEH∽△OFA，
∴，
又∵O为AC的中点，OH∥AB．
∴OH为△ABC的中位线，
∴OH＝AB＝，OA＝OC＝AC＝2，
∴＝＝，
故OF：OE的值为．
【点评】本题考查了相似三角形的判定和性质，直角三角形的性质，灵活运用这些性质解决问题是本题的关键．