辽宁省锦州市2023-2024学年下学期九年级开学验收数学试卷

这是一份辽宁省锦州市2023-2024学年下学期九年级开学验收数学试卷，共11页。试卷主要包含了下列温度比﹣5℃低的是，观察下列尺规作图的痕迹等内容，欢迎下载使用。

1．下列温度比﹣5℃低的是（ ）
A．﹣3℃B．﹣8℃C．0℃D．3℃
2．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A． B． C． D．
3．下面括号内填入m4后，等式成立的是（ ）
A．（ ）+m2＝m6 B．m3•（ ）＝m12 C．（ ）3＝m7 D．m12÷（ ）＝m8
4．中国有悠久的金石文化，印信是金石文化的代表之一，南北朝时期的官员独孤信的印信是迄今发现的中国古代唯一一枚楷书印．它的表面均由正方形和等边三角形组成（如图1），可以看成图2所示的几何体．从正面看该几何体得到的平面图形是（ ）
A．B．C．D．
5．甲、乙两名同学在一次用频率去估计概率的实验中，统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的实验可能是（ ）
A．抛一枚硬币，出现正面的概率 B．掷一枚正方体的骰子，出现6点的概率
C．从一副扑克牌中任意抽取一张是红桃的概率 D．任意写一个正整数，它能被3整除的概率
5题 6题
6．如图，利用标杆BE测量建筑物的高度．如果标杆BE高1.2m，测得AB＝1.6m，BC＝12m，则楼高CD是（ ）
A．9mB．9.6mC．10.2mD．11.2m
7．如图，已知AB∥CD，∠A＝56°，则∠1度数是（ ）
A．56°B．124°C．134°D．146°
8．如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙O交于点D，连接OD．若∠C＝46°，则∠AOD的度数为（ ）
A．44°B．88°C．46°D．92°
7题 8题 10题
9．观察下列尺规作图的痕迹：其中，能够说明AB＞AC的是（ ）
A． B． C． D．
10．如图，正方形ABCD和⊙O的周长之和为20cm，设圆的半径为x cm，正方形的边长为y cm，阴影部分的面积为S cm2．当x在一定范围内变化时，y和S都随x的变化而变化，则y与x，S与x满足的函数关系分别是（ ）
A．一次函数关系，一次函数关系 B．一次函数关系，二次函数关系
C．二次函数关系，二次函数关系 D．二次函数关系，一次函数关系
二．填空题（共5小题，每小题3分，共15分）
11．在2020年年末我国完成了农村贫困人口全部脱贫．为了统计农村贫困人口的数量，国家统计局采取的调查方式是 （填“普查”或“抽样调查”）．
12．如图，在数轴上有A、B、C、D四个点，且BC＝2AB＝3CD，若A、D两点表示的数分别为﹣5和6，那么B点所表示的数是 ．
13．已知关于x的方程x2﹣kx+1＝0有两个相等的实数根，则k的值是 ．
14．如图，点A为反比例函数y=8x（x＞0）上一点，连接OA，交反比例函数y=2x（x＞0）于点B，点C是x轴上一点，且AO＝AC，则△ABC的面积为 ．
15．如图，平行四边形ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，连接EF，给出下列判断：①若△AEF是等边三角形，则∠B＝60°，②若∠B＝60°，则△AEF是等边三角形，③若AE＝AF，则平行四边形ABCD是菱形，④若平行四边形ABCD是菱形，则AE＝AF，其中，结论正确的是 （只需填写正确结论的序号）．
14题 15题
三．解答题（共8小题，共75分）
16．计算（每小题5分，共10分）
（1）计算：2sin60°-3tan30°+(13)0+(-1)2024．
（2）解方程：x2﹣2x﹣1＝0；
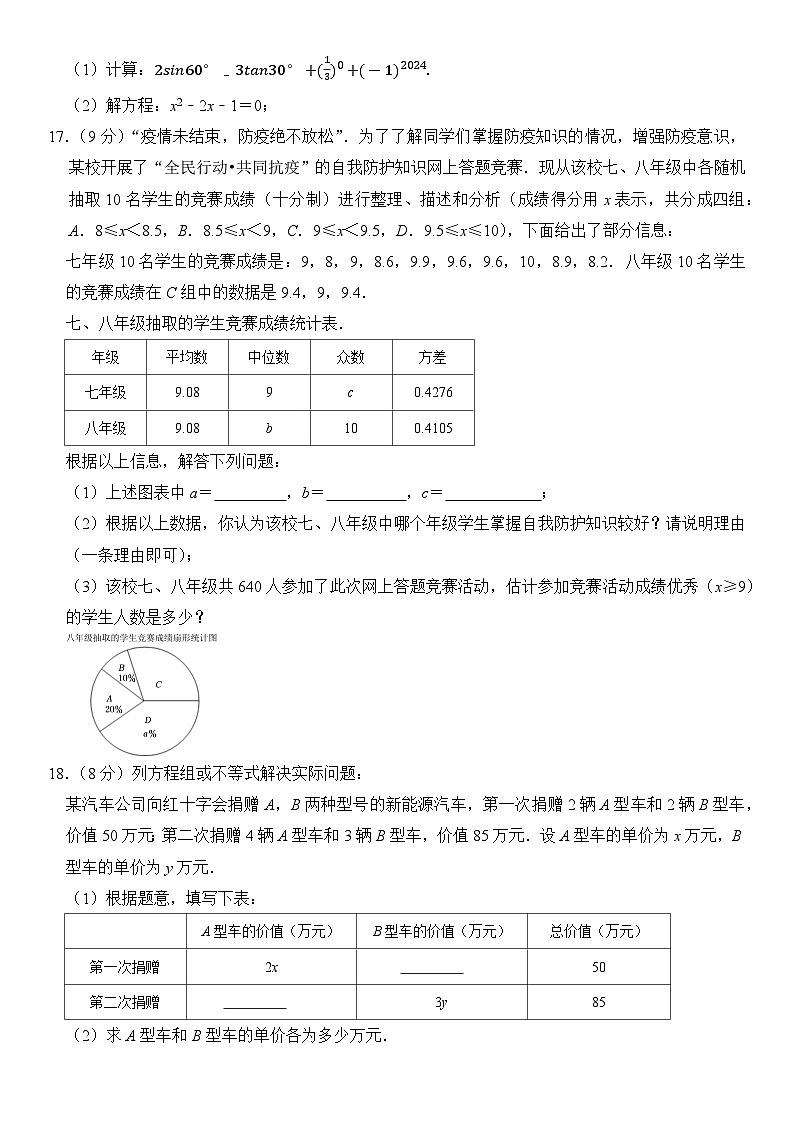
17．（9分）“疫情未结束，防疫绝不放松”．为了了解同学们掌握防疫知识的情况，增强防疫意识，某校开展了“全民行动•共同抗疫”的自我防护知识网上答题竞赛．现从该校七、八年级中各随机抽取10名学生的竞赛成绩（十分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：A．8≤x＜8.5，B．8.5≤x＜9，C．9≤x＜9.5，D．9.5≤x≤10），下面给出了部分信息：
七年级10名学生的竞赛成绩是：9，8，9，8.6，9.9，9.6，9.6，10，8.9，8.2．八年级10名学生的竞赛成绩在C组中的数据是9.4，9，9.4．
七、八年级抽取的学生竞赛成绩统计表．
根据以上信息，解答下列问题：
（1）上述图表中a＝ ，b＝ ，c＝ ；
（2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握自我防护知识较好？请说明理由（一条理由即可）；
（3）该校七、八年级共640人参加了此次网上答题竞赛活动，估计参加竞赛活动成绩优秀（x≥9）的学生人数是多少？
18．（8分）列方程组或不等式解决实际问题：
某汽车公司向红十字会捐赠A，B两种型号的新能源汽车，第一次捐赠2辆A型车和2辆B型车，价值50万元；第二次捐赠4辆A型车和3辆B型车，价值85万元．设A型车的单价为x万元，B型车的单价为y万元．
（1）根据题意，填写下表：
（2）求A型车和B型车的单价各为多少万元．
（3）该公司若准备再次捐赠A，B两种型号的新能源汽车共8辆，且价值不多于100万元，那么A型号汽车的应不少于 辆．
19．（8分）某数学兴趣小组测量商丘地标“玄鸟雕塑”的高度．如图，他们选取的测量点C与“玄鸟雕塑”AB的底部B在同一水平线上．已知雕塑底部BD为5m，在C处测得“玄鸟雕塑”最高处A的仰角∠ACB＝45°，沿BC方向前进10m到达E处，又测得雕塑底部D处的仰角∠DEB＝8°，求“玄鸟雕塑”AD的高度（结果精确到1m，参考数据：sin8°≈0.14，cs8°≈0.99，tan8°≈0.14，tan82°≈7.12）．
20．（8分）如图，四边形ABCD内接于⊙O，AE⊥CB的延长线于点E，连结AC，BD，AB平分∠EBD，
（1）求证：AC＝AD．
（2）当B为AC的中点，BC＝3BE，AD＝6时，求CD的长．
21．（8分）如图1，四边形ABCD，∠A＝90°，AB＝3，BC＝13，CD＝12，DA＝4．
（1）求四边形ABCD的面积；
（2）如图2，以A为坐标原点，以AB、AD所在直线为x轴、y轴建立直角坐标系．
①点P在y轴上，若S△PBD=14S四边形ABCD，求P的坐标；
②点Q在x轴上，若△QBD为等腰三角形，直接写出点Q的坐标．
22．（12分）问题情境：“综合与实践”课上，老师提出如下问题：
将图1中的矩形纸片沿对角线剪开，得到两个全等的三角形纸片，表示为△ABC和△DFE，其中∠ACB＝∠DEF＝90°，∠A＝∠D．将△ABC和△DFE按图2所示方式摆放，其中点B与点F重合（标记为点B）．当∠ABE＝∠A时，延长DE交AC于点G．
（1）试判断四边形BCGE的形状，并说明理由；
（2）深入探究：老师将图2中的△DBE绕点B逆时针方向旋转，使点E落在△ABC内部．
①“善思小组”提出问题：如图3，当∠ABE＝∠BAC时，过点A作AM⊥BE交BE的延长线于点M，BM与AC交于点N．试猜想线段AM和BE的数量关系，并加以证明；
②“智慧小组”提出问题：如图4，当∠CBE＝∠BAC时，过点A作AH⊥DE于点H，若BC＝9，AC＝12，求AH的长．
23．（12分）如图所示，在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）的顶点坐标为C（3，6），并与y轴交于点B（0，3），点A是对称轴与x轴的交点．
（1）求抛物线的解析式；
（2）如图①所示，P是抛物线上的一个动点，且位于第一象限，连接BP，AP，求△ABP的面积的最大值；
（3）如图②所示，在对称轴AC的右侧作∠ACD＝30°交抛物线于点D，直接写出D点的坐标．
参考答案
一．选择题（共10小题）
1．B．2．A．3．D．4．D．5．D．6．C．7．B．8．B．9．D．10．B．
二．填空题（共5小题）
11．普查．12．﹣2．13．2或﹣2．14．4．15．①③④．
三．解答题（共8小题）
16．解：（1）2；
（2）x1=1+2，x2=1-2．
17．解：（1）∵八年级10名学生的竞赛成绩在C组中的数据是9.4，9，9.4，共3个数据，
∴C组所占的百分比为：3÷10＝0.3＝30%，
∴a%＝1﹣30%﹣10%﹣20%＝40%，
∴a＝40，
八年级10名学生的竞赛成绩处于中间的两个数据为9.4，9.4，
∴中位数b=9.4+9.42=9.4，
七年级10名学生的竞赛成绩是：9，8，9，8.6，9.9，9.6，9.6，10，8.9，8.2，
∵9和9.6出现的次数最多，
∴众数c＝9和9.6．
故答案为：40，9.4，9和9.6；
（2）八年级学生掌握自我防护知较好，理由：
∵七年级的方差为0.4276，八年级的方差是0.4105，而0.4276＞0.4105，
∴八年级学生的成绩较为稳定，
∴八年级学生掌握自我防护知较好（答案不唯一，有道理即可）；
（3）640×7+620=416（人）
答：参加竞赛活动成绩优异的学生人数是416人．
18．解：（1）∵第一次捐赠2辆A型车和2辆B型车，第二次捐赠4辆A型车和3辆B型车，
∴第一次捐赠B型车的价值为2y万元，第二次捐赠A型车的价值为4x万元．
故答案为：2y；4x．
（2）依题意得：2x+2y=504x+3y=85，
解得：x=10y=15．
答：A型车的单价为10万元，B型车的单价为15万元．
（3）设捐赠A型车m辆，则捐赠B型车（8﹣m）辆，
依题意得：10m+15（8﹣m）≤100，
解得：m≥4．
∵m为整数，
∴m的最小值为4．
故答案为：4．
19．解：设AB＝x，
在Rt△ABC中，∠ACB＝45°，
∴∠CAB＝45°，
∴AB＝BC＝x，
在Rt△BED中，∠DEB＝8°，BE＝BC+CE＝x+10，BD＝5，
∴tan∠DEB=BDBE，即0.14≈5x+10，
解得x≈25.7，即AB＝25.7，
∴AD＝25.7﹣5＝20.7≈21（m），
答：“玄鸟雕塑”AD的高度为21m．
20．（1）证明：∵四边形ABCD内接于⊙O，
∴∠ADC+∠ABC＝180°，
∵∠ABE+∠ABC＝180°，
∴∠ABE＝∠ADC，
∵AB平分∠DBE，
∴∠ABE＝∠DBA，
∴∠ADC＝∠DBA，
∵∠ACD＝∠DBA，
∴∠ADC＝∠ACD，
∴AC＝AD；
（2）解：过A作AF⊥CD于F，
∵B为AC的中点，
∴AB＝BC，
∵BC＝3BE，
∴AB＝3BE，
∵四边形ABCD是⊙O的内接四边形，
∴∠ADF＝∠ABE，
∵∠AFD＝∠AEB＝90°，
∴△ABE∽△ADF，
∴DFAD=BEAB=13，
∵AD＝6，
∴DF＝2，
∵AC＝AD，
∴CD＝2DF＝4．
21．解：（1）：如图1：连接BD，
在Rt△DAB中，∠A＝90°，由勾股定理得，DB=DA2+AB2=42+32=5，
在△BDC中，BD2+DC2＝52+122＝169＝132＝BC2，
∴△BDC为直角三角形，∠CDB＝90°，
S四边形ABCD＝S△DAB+S△BDC=12BA•DA+12BD•DC=12×3×4+12×5×12＝36；
（2）①如图：由（1）知：S△PBD=14S四边形ABCD=9，
S△PBD=12PD•BA=12PD•3＝9，PD＝6，
∵D（0，4），
∴AP＝AD﹣DP＝﹣2或AP＝AD+DP＝10，
∴P（0，10）或（0，﹣2）．
②设Q点坐标为（b，0），则B（3，0），D（0，4），
∴QB2＝（b﹣3）2、DB2＝32+42＝25，QD2＝b2+42
当QB＝BD时，QB2＝BD2，即（b﹣3）2＝25，
解得：b＝8或﹣2，
∴Q的坐标为（﹣2，0）或（8，0）；
当QB＝QD时，QB2＝QD2，即（b﹣3）2＝b2+42，
解得：b=-76；
∴Q的坐标为(-76，0)；
当BD＝QD时，BD2＝QD2，即25＝b2+42，
解得：b＝﹣3或3（舍去）；
∴Q的坐标为（﹣3，0）．
综上，点Q的坐标为（﹣2，0）或（8，0）或(-76，0)或（﹣3，0）．
22．解：（1）四边形BCGE为正方形．理由如下：
∵∠BED＝90°，
∴∠BEG＝180°﹣∠BED＝90°，
∵∠ABE＝∠A，
∴AC∥BE，
∴∠CGE＝∠BED＝90°，
∵∠C＝90°，
∴四边形BCGE为矩形，
∵△ACB≌△DEB，
∴BC＝BE，
∴矩形BCGE为正方形；
（2）①AM＝BE，理由如下：
∵∠ABE＝∠BAC，
∴AN＝BN，
∵∠C＝90°，
∴BC⊥AN，
∵AM⊥BE，即AM⊥BN，
∴S△ABN=12AN•BC=12BN•AM，
∵AN＝BN，
∴BC＝AM，
由（1）得BE＝BC，
∴AM＝BE；
②如图4，设AB，DE的交点为M，过M作MG⊥BD于G，
∵△ACB≌△DEB，
∴BE＝BC＝9，DE＝AC＝12，∠BAC＝∠D，∠ABC＝∠DBE，
∴∠CBE＝∠DBM；
∵∠CBE＝∠BAC，
∴∠DBM＝∠BAC，
∴∠DBM＝∠D，
∴MD＝MB，
∵MG⊥BD，
∴点G是BD的中点；
由勾股定理得AB=AC2+BC2=15，
∴DG=12BD=152；
∵csD=DGDM=DEBD，
∴DM=DG⋅BDDE=152×1512=758，即BM＝DM=758；
∴AM＝AB﹣BM＝15-758=458；
∵AH⊥DE，BE⊥DE，
∴∠AHM＝∠BEM＝90°，
∵∠AMH＝∠BME，
∴△AMH∽△BME，
∴AHBE=AMBM=35，
∴AH=35BE=35×9=275，即AH的长为275．
23．解：（1）抛物线顶点坐标为C（3，6），
∴可设抛物线解析式为y＝a（x﹣3）2+6，
将B（0，3）代入可得a=-13，
∴y=-13x2+2x+3；
（2）连接PO，
由题意，BO＝3，AO＝3，
设P（n，-13n2+2n+3），
∴S△ABP＝S△BOP+S△AOP﹣S△ABO，
S△BPO=32n，
S△APO=-12n2+3n+92，
S△ABO=92，
∴S△ABP＝S△BOP+S△AOP﹣S△ABO=-12n2+92n=-12（n-92）2+818，
∴当n=92时，S△ABP的最大值为818；
（3）存在，设D点的坐标为（t，-13t2+2t+3），
过D作对称轴的垂线，垂足为G，
则DG＝t﹣3，CG＝6﹣（-13t2+2t+3）=13t2﹣2t+3，
∵∠ACD＝30°，
∴2DG＝DC，
在Rt△CGD中，
CG=3DG，
∴3（t﹣3）=13t2﹣2t+3，
∴t＝3+33或t＝3（舍）
∴D（3+33，﹣3）．年级
平均数
中位数
众数
方差
七年级
9.08
9
c
0.4276
八年级
9.08
b
10
0.4105
A型车的价值（万元）
B型车的价值（万元）
总价值（万元）
第一次捐赠
2x

50
第二次捐赠

3y
85