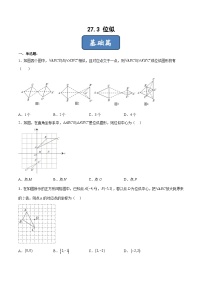
初中人教版28.1 锐角三角函数一课一练

这是一份初中人教版28.1 锐角三角函数一课一练，共26页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题：
1．下列三角函数的值是的是（ ）．
A．B．C．D．
2．已知，则锐角α的度数是（ ）
A．60°B．45°C．30°D．75°
3．在中，，若，则的值为（ ）
A．B．C．2D．
4．下列各式中不成立的是（ ）
A．B．
C．D．
5．若，则的形状是（ ）
A．直角三角形B．等边三角形C．钝角三角形D．等腰直角三角形
6．式子的值是（ ）
A．0B．C．2D．
7．若菱形的周长为，高为2，则菱形两邻角的度数比为（ ）
A．6：1B．5：1C．4：1D．3：1
二、填空题：
8．已知是锐角，，则＝______；______．
9．在Rt△ABC中，∠ACB＝90°，若∠A＝60°，AC＝6，则＝____．
10．已知，则锐角________．
11．计算：___________．
12．﹣|tan45°﹣|＝_____．
13．在中，若 ，则的度数为__________
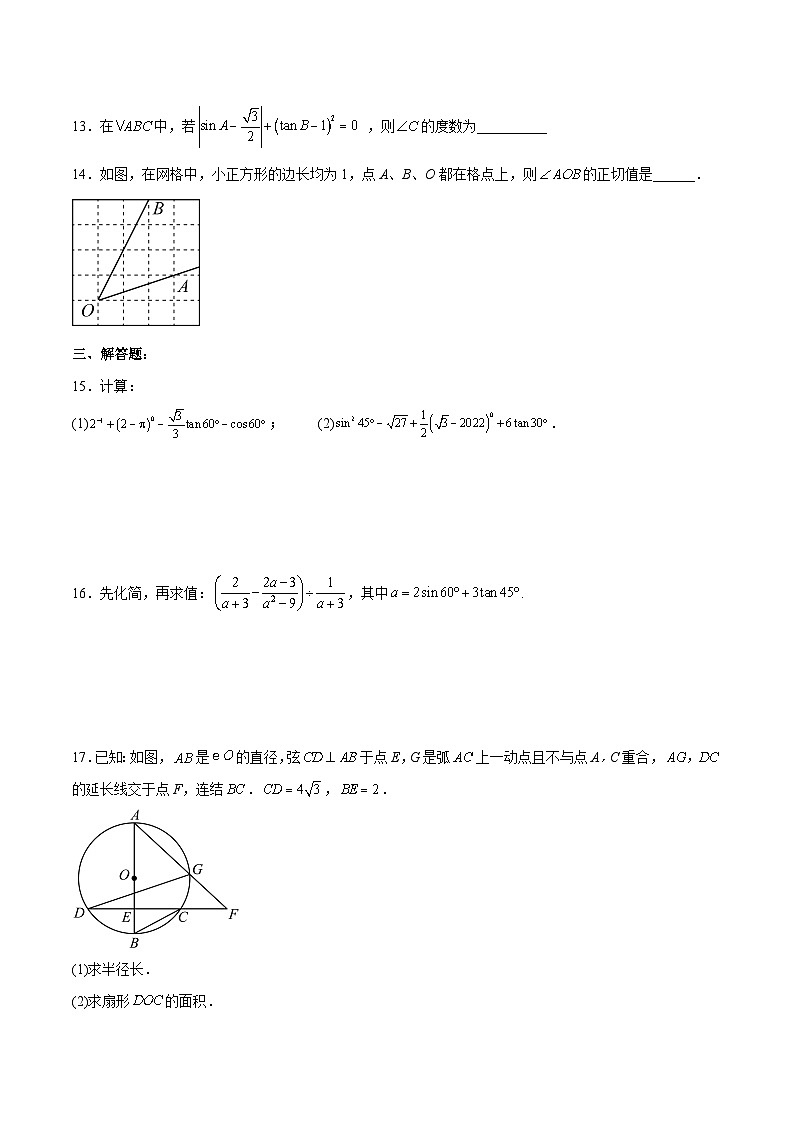
14．如图，在网格中，小正方形的边长均为1，点A、B、O都在格点上，则的正切值是______．

三、解答题：
15．计算：
(1)； (2)．
16．先化简，再求值：，其中.
17．已知：如图，是的直径，弦于点E，G是弧上一动点且不与点A，C重合，的延长线交于点F，连结．，．
(1)求半径长．
(2)求扇形的面积．
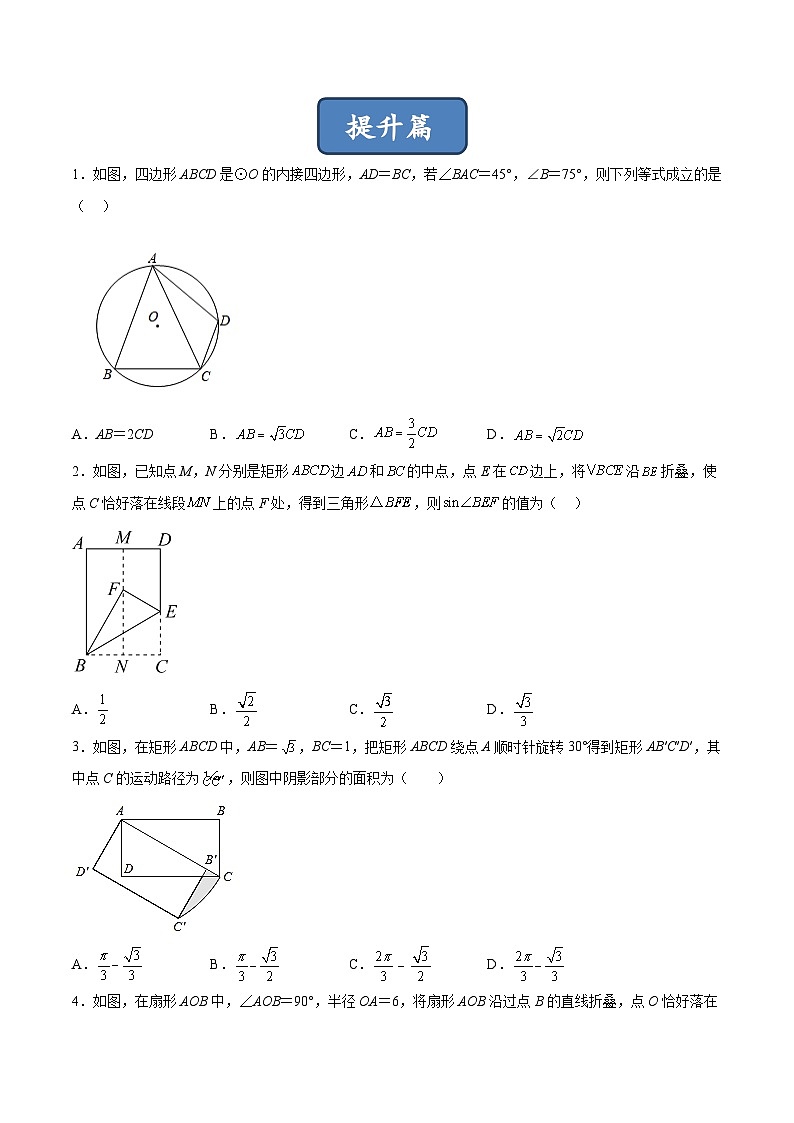
提升篇
1．如图，四边形ABCD是⊙O的内接四边形，AD＝BC，若∠BAC＝45°，∠B＝75°，则下列等式成立的是（ ）
A．AB＝2CDB．C．D．
2．如图，已知点M，N分别是矩形边和的中点，点E在边上，将沿折叠，使点C恰好落在线段上的点F处，得到三角形，则的值为（ ）
A．B．C．D．
3．如图，在矩形ABCD中，AB＝，BC＝1，把矩形ABCD绕点A顺时针旋转30°得到矩形AB′C′D′，其中点C的运动路径为，则图中阴影部分的面积为（ ）
A．B．C．D．
4．如图，在扇形AOB中，∠AOB＝90°，半径OA＝6，将扇形AOB沿过点B的直线折叠，点O恰好落在弧AB上点D处，折痕交OA于点C，整个阴影部分的面积______．
5．如图，四边形是正方形，以为边向外作为上的一点，连接．若四边形是菱形，则的度数为________．
6．如图，中，，顶点A，B分别在反比例函数与的图象上，则的度数为______．
7．如图，在平行四边形ABCD中，过点A作，垂是为E，连接DE，F为线段DE上一点，且∠AFE＝∠B
(1)求证：；
(2)若，求∠ADE的度数．
8．已知：如图，在中，，cm，cm，为边上的高，点从点出发，沿方向匀速运动，速度为cm/s；同时，点从点出发，沿方向匀速运动，速度为cm/s．设运动时间为．
解答下列问题：
(1)当为何值时，；
(2)当中点在上时，求的值；
(3)设四边形的面积为，求与的函数关系式，并求最小值；
(4)是否存在某一时刻，使得，若存在，求出的值；若不存在，请说明理由．
28.1.3 特殊角的三角函数值
基础篇
一、单选题：
1．下列三角函数的值是的是（ ）．
A．B．C．D．
【答案】A
【分析】根据特殊角的三角函数值解答．
【详解】A、＝，符合题意；
B、＝，不符合题意；
C、＝，不符合题意；
D、＝，不符合题意；
故选A．
【点睛】本题考查特殊角的三角函数值，准确掌握常见的特殊角的三角函数值是解题的关键．
2．已知，则锐角α的度数是（ ）
A．60°B．45°C．30°D．75°
【答案】A
【分析】根据得到即可求解．
【详解】解：∵，为锐角，
∴，
∴，
故选：A．
【点睛】本题考查根据特殊角三角函数值求角的度数，熟记特殊角的三角函数值是解答的关键．
3．在中，，若，则的值为（ ）
A．B．C．2D．
【答案】A
【分析】在直角三角形中，求出的度数，即可求．
【详解】解：如图所示，∵，，
∴，
∵，
∴，
∴．
故选：A．
【点睛】本题考查了锐角三角函数，解决本题的关键是掌握特殊角的三角函数值．
4．下列各式中不成立的是（ ）
A．B．
C．D．
【答案】D
【分析】根据特殊锐角三角函数值，代入计算即可．
【详解】A．，此选项不符合题意；
B．，，所以，此选项不符合题意；
C．，，所以，此选项不符合题意；
D．，此选项符合题意；
故选：D．
【点睛】本题考查特殊锐角三角函数值，掌握特殊锐角三角函数值是正确解答的前提．
5．若，则的形状是（ ）
A．直角三角形B．等边三角形C．钝角三角形D．等腰直角三角形
【答案】C
【分析】根据非负数的性质得到，再由特殊角的三角函数值求出的度数，再判断即可．
【详解】解：∵，
∴，
即，
由特殊角的三角函数值可知此时，
此时，
则的形状是钝角三角形，
故选C．
【点睛】本题考查了非负数的性质和特殊角的三角函数值，熟记特殊角的三角函数值是解题的关键．
6．式子的值是（ ）
A．0B．C．2D．
【答案】A
【分析】根据特殊角的三角函数值计算即可．
【详解】解：原式
=0
故选：A．
【点睛】本题考查特殊角的三角函数值及二次根式的混合运算，解题关键是熟练掌握特殊角的三角函数值．
7．若菱形的周长为，高为2，则菱形两邻角的度数比为（ ）
A．6：1B．5：1C．4：1D．3：1
【答案】D
【分析】如图，为菱形的高，，利用菱形的性质得到，利用正弦的定义得到，则，从而得到的比值．
【详解】解：如图，为菱形的高，，
菱形的周长为，
，
在中，，
，
，
，
．
故选：D．
【点睛】本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．也考查了直角三角形斜边上的中线性质．
二、填空题：
8．已知是锐角，，则＝______；______．
【答案】 60°##60度 ##0.5
【分析】根据特殊角的三角函数值，计算求值即可.
【详解】解：∵，
∴，
∵是锐角，
∴，
∴，
故答案为：60°，.
【点睛】本题考查了60°的正切和余弦，熟记特殊角的三角函数值是解题关键．
9．在Rt△ABC中，∠ACB＝90°，若∠A＝60°，AC＝6，则＝____．
【答案】##0.5
【分析】利用直角三角形的两锐角互余求得∠ABC的度数，再利用特殊角的三角函数即可求得的值．
【详解】解：依照题意画出图形，如图所示．
∵在Rt△ABC中，，，
∴，
∴．
故答案为∶．
【点睛】考查了直角三角形的性质及特殊角的三角函数值，熟练掌握直角三角形的两锐角互余是解题的关键．
10．已知，则锐角________．
【答案】
【分析】先由变形为，即可求解．
【详解】解：，
，
，
．
故答案为：．
【点睛】本题主要考查了特殊角的三角函数值，灵活变形，熟记公式是解题的关键．
11．计算：___________．
【答案】##0.75
【分析】将特殊角的三角函数值代入原式，即可求解．
【详解】解：
，
故答案为：．
【点睛】本题主要考查特殊角三角函数值的混合运算、二次根式的混合运算，掌握特殊角的三角函数值是解题的关键．
12．﹣|tan45°﹣|＝_____．
【答案】
【分析】根据零指数幂的意义、负整数指数幂的意义，二次根式的性质、特殊角的三角函数值以及绝对值的定义解答即可．
【详解】原式＝
=
=
故答案为：．
【点睛】本题考查了实数的混合运算．掌握零次幂，负指数幂，特殊角的三角函数以及绝对值的定义是解答本题的关键．
13．在中，若 ，则的度数为__________
【答案】##75度
【分析】根据非负数的性质得出，，根据特殊角的三角函数值、三角形内角和定理计算即可．
【详解】解：∵
∴，，
∴，，
∴，
∴，
故答案为：．
【点睛】本题考查的是特殊角的三角函数值，熟记特殊角的三角函数值、非负数的性质是解题的关键．
14．如图，在网格中，小正方形的边长均为1，点A、B、O都在格点上，则的正切值是______．

【答案】1
【分析】连接AB，由勾股定理求得AB、AO、BO的长，判断△ABO是等腰直角三角形，即可求得答案．
【详解】解：连接AB，
由勾股定理得：AB＝，AO＝，OB＝，
∴AB＝AO，，
∴△ABO是以OB为斜边的等腰直角三角形，
∴，
故答案为：1．
【点睛】此题考查了勾股定理在网格中的应用、勾股定理的逆定理、等腰直角三角形的性质、特殊角的三角函数值等知识，熟练掌握勾股定理及其逆定理是解题的关键．
三、解答题：
15．计算：
(1)；
(2)．
【答案】(1)0
(2)
【分析】（1）先化简各式，然后再进行计算即可解答；
（2）先化简各式，然后再进行计算即可解答．
【详解】（1）解：
；
（2）解：
．
【点睛】本题考查了实数的运算，零指数幂，负整数指数幂，特殊角的三角函数值，准确熟练地进行计算是解题的关键．
16．先化简，再求值：，其中.
【答案】，
【分析】先根据分式的减法法则进行计算，再根据分式的除法进行计算，最后代入求出答案即可．
【详解】解：原式
∵
∴原式
【点睛】本题考查了特殊三角函数值和分式的化简与求值，能正确根据分式的运算法则进行化简是解此题的关键，注意运算顺序．
17．已知：如图，是的直径，弦于点E，G是弧上一动点且不与点A，C重合，的延长线交于点F，连结．，．
(1)求半径长．
(2)求扇形的面积．
【答案】(1)4
(2)
【分析】（1）连接．设的半径为R．在中，根据，构建方程即可解决问题；
（2）连接，根据可得，再由垂径定理可得，根据扇形的面积公式求解即可．
【详解】（1）解：如图，连接．设的半径为R．
∵，
∴，
在中，
∵，
∴，
解得．
（2）解：如图，连接，
∵，
∴，
∵，
∴
∴，
∴扇形的面积．
【点睛】本题考查的是特殊角的三角函数、圆周角定理的推论和垂径定理的应用，掌握圆周角定理的推论、垂径定理和勾股定理是解题的关键，学会添加常用辅助线．
提升篇
1．如图，四边形ABCD是⊙O的内接四边形，AD＝BC，若∠BAC＝45°，∠B＝75°，则下列等式成立的是（ ）
A．AB＝2CDB．C．D．
【答案】B
【分析】连接OB、OC，过O作AB的垂线，垂足为E，交CD于点F．由已知可得AB∥CD，则OF⊥CD，且∠BOC=90°，E、F分别是AB、CD的中点；易证△BOE≌△OCF，从而BE与CF的关系，即可得AB与CD的关系．
【详解】如图，连接OB、OC，过O作AB的垂线，垂足为E，交CD于点F．
∵AD=BC，
∴，
∴∠ACD=∠BAC=45°．
∴AB∥CD．
∵OE⊥AB，
∴AB=BE，OF⊥CD．
∴CD=2CF．
∵∠BAC、∠BOC对着同一弧，
∴∠BOC=2∠BAC=90°．
∴∠EOB+∠COF=90°．
∵∠EOB+∠OBE =90°，
∴∠OBE=∠COF．
∵∠OEB=∠CFO=90°，OB=OC，
∴△BOE≌△OCF．
∴OE=CF．
∵OB=OC，
∴∠OBC=45°．
∵∠ABC=75°，
∴∠OBE=∠ABC-∠OBC=30°．
∴．
∴．
∵AB=2BE，CD=2CF，
∴．
故选：B．
【点睛】本题考查了圆周角定理，垂径定理，全等三角形的判定与性质，三角函数等知识，构造辅助线并证明△BOE≌△OCF是问题的关键．
2．如图，已知点M，N分别是矩形边和的中点，点E在边上，将沿折叠，使点C恰好落在线段上的点F处，得到三角形，则的值为（ ）
A．B．C．D．
【答案】C
【分析】先证四边形是矩形，得到，由折叠的性质可，，，得到，可以得到，则，得，即可得到答案．
【详解】解：∵四边形是矩形，
∴，，，
∵点M，N分别是矩形边和的中点，
∴，，
∴四边形是矩形，
∴，
∵沿折叠，使点C恰好落在线段上的点F处，得到三角形，
∴，，，
∵，
∴，
∴，
∴，
∴，
故选：C
【点睛】此题考查了矩形的判定和性质、特殊角的三角函数、折叠的性质等知识，熟练掌握折叠的性质是解题的关键．
3．如图，在矩形ABCD中，AB＝，BC＝1，把矩形ABCD绕点A顺时针旋转30°得到矩形AB′C′D′，其中点C的运动路径为，则图中阴影部分的面积为（ ）
A．B．C．D．
【答案】B
【分析】连接AC'，首先求出tan∠BAC，然后根据勾股定理求出AC的长，最后根据S阴＝S扇形ACC′﹣S△AB′C′代入数值即可求解．
【详解】连接AC'，
在矩形ABCD中，∵∠B＝90°，AB＝，BC＝1，
∴tan∠BAC＝＝，
∴∠BAC＝30°，
∵旋转角为30°，
∴A、B′、C共线．
∴AC＝＝＝2，
∵S阴＝S扇形ACC′﹣S△AB′C′，
∴S阴＝﹣＝﹣，
故选：B．
【点睛】本题考查了矩形的性质，扇形的面积，锐角三角函数，关键是要作出辅助线将阴影面积转化成扇形面积减去三角形面积．
4．如图，在扇形AOB中，∠AOB＝90°，半径OA＝6，将扇形AOB沿过点B的直线折叠，点O恰好落在弧AB上点D处，折痕交OA于点C，整个阴影部分的面积______．
【答案】
【分析】首先连接OD，由折叠的性质，可得CD=CO，BD=BO，∠DBC=∠OBC，则可得△OBD是等边三角形，继而求得OC的长，即可求得△OBC与△BCD的面积，又在扇形OAB中，∠AOB=90°，半径OA=6，即可求得扇形OAB的面积，继而求得阴影部分面积．
【详解】解：如图，连接OD，
根据折叠的性质，CD=CO，BD=BO，∠DBC=∠OBC，
∴OB=OD=BD，
即△OBD是等边三角形，
∴∠DBO=60°，
∴∠CBO=∠DBO=30°，
∵∠AOB=90°，
∴OC=OB•tan∠CBO=6，
∴S△BDC=S△OBC=×OB×OC=×6×=6，
S扇形AOB=π×62=9π，
∴整个阴影部分的面积为：S扇形AOB-S△BDC-S△OBC=9π-6-6=9π-12，
故答案为：.
【点睛】本题考查了折叠的性质、扇形面积公式以及直角三角形的性质．此题难度适中，注意数形结合思想的应用，注意辅助线的作法．
5．如图，四边形是正方形，以为边向外作为上的一点，连接．若四边形是菱形，则的度数为________．
【答案】##15度
【分析】过点作的垂线，垂足分别为，四边形是矩形，得出，可得，进而即可求解．
【详解】∵四边形是正方形，
∴，，
如图，过点作的垂线，垂足分别为，
∴四边形是矩形，
∵四边形是菱形，
∴
∴，
∴，
∴．
【点睛】本题考查了菱形的性质，矩形的性质，正方形的性质，特殊角的三角函数值，求得是解题的关键．
6．如图，中，，顶点A，B分别在反比例函数与的图象上，则的度数为______．
【答案】##60度
【分析】过A作轴于C，过B作轴于D，得到，根据反比例函数的性质得到，，根据相似三角形的面积比等于相似比的平方即可求出与的比值，从而得到的值，即可得到的值
【详解】过A作轴于C，过B作轴于D，
则，
∵顶点A，B分别在反比例函数与的图象上,
∴，，
∵，
∴，
∴，
∴，
∴，
∴，
∴，
∴
故答案为：．
【点睛】本题考查了相似三角形的判定与性质、反比例函数的性质以及直角三角形的性质．解题时注意掌握数形结合思想的应用，注意掌握辅助线的作法．
7．如图，在平行四边形ABCD中，过点A作，垂是为E，连接DE，F为线段DE上一点，且∠AFE＝∠B
(1)求证：；
(2)若，求∠ADE的度数．
【答案】(1)证明见解析；
(2)．
【分析】（1）易证∠ADF=∠CED和∠AFD=∠DCE，即可证明△ADF∽△DEC．
（2）根据平行四边形对边相等可求得CD的长，根据△ADF∽△DEC可得，即可求得DE的长，根据勾股定理可以求得AE的长，根据tan∠ADE=即可解题．
(1)
证明：∵平行四边形ABCD中，AB∥CD，AD∥BC，
∴∠B+∠DCE=180°，∠ADF=∠CED，
∵∠B=∠AFE，∠AFD+∠AFE=180°，
∴∠AFD=∠DCE，
∴△ADF∽△DEC；
(2)
解：∵四边形ABCD为平行四边形，
∴CD=AB，AD∥BC，
∴，
∵
∴AE⊥AD，
∵△ADF∽△DEC，，
∴，即，
∴DE=12，
∵在RT△ADE中，AE2=DE2-AD2，
∴AE=6，
∴，
∴ ．
【点睛】本题考查了相似三角形的判定和性质、平行四边形对边平行且相等的性质、勾股定理等知识，解题的关键是证明△ADF∽△DEC，学会转化的思想．
8．已知：如图，在中，，cm，cm，为边上的高，点从点出发，沿方向匀速运动，速度为cm/s；同时，点从点出发，沿方向匀速运动，速度为cm/s．设运动时间为．
解答下列问题：
(1)当为何值时，；
(2)当中点在上时，求的值；
(3)设四边形的面积为，求与的函数关系式，并求最小值；
(4)是否存在某一时刻，使得，若存在，求出的值；若不存在，请说明理由．
【答案】(1)；
(2)s；
(3)，取得最小值为；
(4)存在某一时刻s，使得
【分析】（1）证明得到，即，求出t即可；
（2）设与相交与点，则为中点，过作于点，利用三角函数求出，进而得到，，，求出，得到，求出t；
（3）根据求出函数解析式，利用二次函数的性质解答；
（4）当时，过作交于，利用等腰三角形三线合一的性质得到，表示出AN、AP，利用三角函数求出t．
（1）
由题意可知，，，
，
，
，
解得，
当时，；
（2）
设与相交与点，则为中点，
过作于点，
，，，
∴csA=，
，
，，，
，
，
，
，
，
s；
（3）

当s时，S取得最小值为；
（4）
当时，过作交于，
则，
，，
，
解得：s．
所以存在某一时刻s，使得．
【点睛】此题考查了相似三角形的判定及性质，三角函数，求函数解析式，二次函数的最值，等腰三角形三线合一的性质，熟记各知识点并综合应用是解题的关键．