

人教版七年级下册5.4 平移当堂检测题
展开【例题讲解】
在平面直角坐标系中,已知点,,连接AB,将AB向下平移5个单位得线段CD,其中点A的对应点为点C.
(1)填空:点C的坐标为______,线段AB平移到CD扫过的面积为______;
(2)若点P是y轴上的动点,连接PD.
①如图(1),当点P在y轴正半轴时,线段PD与线段AC相交于点E,用等式表示三角形PEC的面积与三角形ECD的面积之间的关系,并说明理由;
②当PD将四边形ACDB的面积分成2:3两部分时,求点P的坐标.
(1)解:将AB向下平移5个单位得线段CD,∴点C(2,-1),
线段AB平移到CD扫过的面积为:故答案为:(2,-1);20;
(2)①如图1,过P点作PF⊥AC于F,
由平移知,轴,∵A(2,4),∴PF=2,
由平移知,CD=AB=4,
∴S△PEC=CE•PF=CE×2=CE,
S△ECD=CE•CD=CE×4=2CE,
∴S△ECD=2S△PEC,即:S△PEC=S△ECD;
②如图2,当PD交线段AC于E,且PD将四边形ACDB分成面积为2:3两部分时,连接PC,延长DC交y轴于点M,则M(0,﹣1),
∴OM=1,连接AD,则S△ACD=S长方形ABDC=10,
∵PD将四边形ACDB的面积分成2:3两部分,
∴S△CDE=S矩形ABDC=×20=8,由①知,S△PEC=S△ECD=×8=4,
∴S△PCD=S△PEC+S△ECD=4+8=12,∵S△PCD=CD•PM=×4PM=12,
∴PM=6,∴PO=PM﹣OM=6﹣1=5,∴P(0,5).
如图3,当PD交AB于点E,PD将四边形ACDB分成面积为2:3两部分时,
连接PB,延长BA交y轴于点G,则G(0,4),
∴OG=4,连接AD,则S△ABD=S长方形ABDC=10,
∵PD将四边形ACDB的面积分成2:3两部分,
∴S△BDE=S矩形ABDC=×20=8,
∵S△BDE=BD•BE=×5BE=8,∴BE=
过P点作PH⊥BD交DB的延长线于点H,
∵B(6,4),∴PH=6
S△PDB=BD×PH=×5×6=15,
∴S△PBE=S△PDB﹣S△BDE=15﹣8=7,
∵S△PBE=BE•PG=PG=7,∴PG=,
∴PO=PG+OG=+4=,∴P(0,),综上可得:P(0,)或P(0,5).
【综合解答】
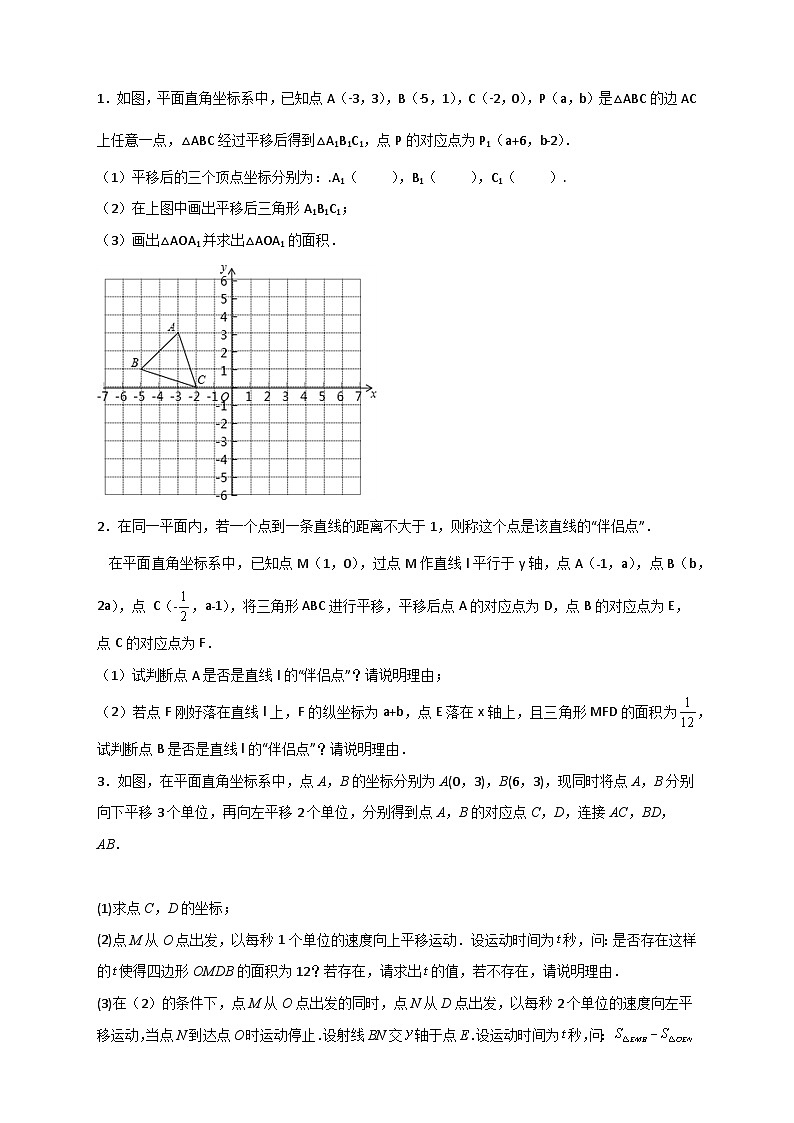
1.如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)平移后的三个顶点坐标分别为:.A1( ),B1( ),C1( ).
(2)在上图中画出平移后三角形A1B1C1;
(3)画出△AOA1并求出△AOA1的面积.
2.在同一平面内,若一个点到一条直线的距离不大于1,则称这个点是该直线的“伴侣点”.
在平面直角坐标系中,已知点M(1,0),过点M作直线l平行于y轴,点A(﹣1,a),点B(b,2a),点 C(﹣,a﹣1),将三角形ABC进行平移,平移后点A的对应点为D,点B的对应点为E,点C的对应点为F.
(1)试判断点A是否是直线l的“伴侣点”?请说明理由;
(2)若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且三角形MFD的面积为,试判断点B是否是直线l的“伴侣点”?请说明理由.
3.如图,在平面直角坐标系中,点A,B的坐标分别为A(0,3),B(6,3),现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
(1)求点C,D的坐标;
(2)点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为秒,问:是否存在这样的使得四边形OMDB的面积为12?若存在,请求出的值,若不存在,请说明理由.
(3)在(2)的条件下,点M从O点出发的同时,点N从D点出发,以每秒2个单位的速度向左平移运动,当点N到达点O时运动停止.设射线BN交轴于点E.设运动时间为秒,问:的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
4.如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系点A(0,a),C(b,0)满足.D为线段AC的中点.在平面直角坐标系中以任意两点P(x 1,y1)、Q(x2,y2)为端点的线段中点坐标为,.
(1)则A点的坐标为 ;点C的坐标为 .D点的坐标为 .
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点 Q 到 达 A 点 整 个 运 动 随 之 结 束 . 设 运 动 时 间 为 t (t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ,若存在,请求出t的值;若不存在,请说明理由.
(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,的值是否会发生变化?若不变,请求出它的值,若变化请说明理由.
5.如图所示,在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是,,,先将向上平移3个单位长度,再向右平移2个单位长度,得到.
(1)在图中画出.
(2)写出点的坐标.
(3)若轴上有一点,使与面积相等,求出点的坐标.
6.在如图所示的直角坐标系中,△ABC的顶点坐标分别是A(﹣2,5),B(﹣4,﹣1)C(2,3),△A1B1C1是由△ABC平移得到,点P(x1,y1)是△ABC内一点,经过平移点P(x1,y1)变成点P1(x1+2,y1﹣1)
(1)写出三个顶点的坐标
(2)请画出平移后的△A1B1C1
(3)求△A1B1C1的面积
7.如图1,在平面直角坐标系中,点是坐标原点,边长为2的正方形(点与点重合)和边长为4的正方形的边和都在轴上,且点坐标为.正方形以3个单位长度/秒的速度沿轴向右运动,记正方形和正方形重叠部分的面积为,假设运动时间为秒,且.
(1)点的坐标为______;
(2)如图2,正方形向右运动的同时,动点在线段上以1个单位长度/秒的速度从到运动.连接,.
①为何值时,所在直线垂直于轴?
②为何值时,?
8.如图,在平面直角坐标系中,已知△ABC中,点A坐标为(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)写出点C的坐标( , )
(2)在y轴上是否存在点P,使得S△POB=S△ABC,若存在,求出点P的坐标;若不存在;
(3)把点C往上平移3个单位得到点H,画射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探索∠BMA、∠HBM、∠MAC之间的数量关系,并证明你的结论.
9.在如图所示的平面直角坐标系中,A(2,3),B(4,0).
(1)将线段AB沿x轴向左平移4个单位长度,再沿y轴向上平移2个单位长度至线段CD(C与A对应),求△ABD的面积;
(2)将线段AB平移至线段PQ(P与B对应),且点P恰好落在y轴上.
①若△ABQ的面积为3,请通过计算说明,线段AB是如何平移至线段PQ的?
②设P(0,y),且-8≤y≤8,请用含y的式子表示△ABP的面积,并求出当y=-8时,△ABP的最大面积.
10.如图,在平面直角坐标系中,已知,,将线段平移至,点在轴正半轴上(不与点重合),连接,,,.
(1)写出点的坐标;
(2)当的面积是的面积的3倍时,求点的坐标;
(3)设,,,判断、、之间的数量关系,并说明理由.
11.如图,在正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为、.
(1)请在如图所示的网格平面内画出平面直角坐标系;
(2)点是边BC上任意一点,三角形经过平移后得到,点P的对应点为.
①直接写出点的坐标 ;
②画出平移后的.
(3)在y轴上是否存在点P,使的面积等于面积的,若存在,请求出点P的坐标;若不存在,请说明理由.
12.如图,在正方形网格中,每个小正方形的边长为1个单位长度,格点(顶点是网格的交点的三角形)的顶点A,C坐标分别为,
(1)请在如图所示的网格内画出对应的平面直角坐标系;
(2)再把先向右平移5个单位长度,再向下平移3个单位长度得到,且点的对应点分别为,请你在图中画出;
(3)在Y轴上是否存在点P,使的面积等于的面积的一半,若存在求出点P的坐标;若不存在说明理由.
13.在平面直角坐标系中,已知点,,连接AB,将AB向下平移5个单位得线段CD,其中点A的对应点为点C.
(1)填空:点C的坐标为______,线段AB平移到CD扫过的面积为______;
(2)若点P是y轴上的动点,连接PD.
①如图(1),当点P在y轴正半轴时,线段PD与线段AC相交于点E,用等式表示三角形PEC的面积与三角形ECD的面积之间的关系,并说明理由;
②当PD将四边形ACDB的面积分成2:3两部分时,求点P的坐标.
专题14 坐标系中的面积(和平移有关)
【例题讲解】
在平面直角坐标系中,已知点,,连接AB,将AB向下平移5个单位得线段CD,其中点A的对应点为点C.
(1)填空:点C的坐标为______,线段AB平移到CD扫过的面积为______;
(2)若点P是y轴上的动点,连接PD.
①如图(1),当点P在y轴正半轴时,线段PD与线段AC相交于点E,用等式表示三角形PEC的面积与三角形ECD的面积之间的关系,并说明理由;
②当PD将四边形ACDB的面积分成2:3两部分时,求点P的坐标.
(1)解:将AB向下平移5个单位得线段CD,∴点C(2,-1),
线段AB平移到CD扫过的面积为:故答案为:(2,-1);20;
(2)①如图1,过P点作PF⊥AC于F,
由平移知,轴,∵A(2,4),∴PF=2,
由平移知,CD=AB=4,
∴S△PEC=CE•PF=CE×2=CE,
S△ECD=CE•CD=CE×4=2CE,
∴S△ECD=2S△PEC,即:S△PEC=S△ECD;
②如图2,当PD交线段AC于E,且PD将四边形ACDB分成面积为2:3两部分时,连接PC,延长DC交y轴于点M,则M(0,﹣1),
∴OM=1,连接AD,则S△ACD=S长方形ABDC=10,
∵PD将四边形ACDB的面积分成2:3两部分,
∴S△CDE=S矩形ABDC=×20=8,由①知,S△PEC=S△ECD=×8=4,
∴S△PCD=S△PEC+S△ECD=4+8=12,∵S△PCD=CD•PM=×4PM=12,
∴PM=6,∴PO=PM﹣OM=6﹣1=5,∴P(0,5).
如图3,当PD交AB于点E,PD将四边形ACDB分成面积为2:3两部分时,
连接PB,延长BA交y轴于点G,则G(0,4),
∴OG=4,连接AD,则S△ABD=S长方形ABDC=10,
∵PD将四边形ACDB的面积分成2:3两部分,
∴S△BDE=S矩形ABDC=×20=8,
∵S△BDE=BD•BE=×5BE=8,∴BE=
过P点作PH⊥BD交DB的延长线于点H,
∵B(6,4),∴PH=6
S△PDB=BD×PH=×5×6=15,
∴S△PBE=S△PDB﹣S△BDE=15﹣8=7,
∵S△PBE=BE•PG=PG=7,∴PG=,
∴PO=PG+OG=+4=,∴P(0,),综上可得:P(0,)或P(0,5).
【综合解答】
1.如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)平移后的三个顶点坐标分别为:.A1( ),B1( ),C1( ).
(2)在上图中画出平移后三角形A1B1C1;
(3)画出△AOA1并求出△AOA1的面积.
【答案】(1)A1 (3,1)B1 (1,-1)C1(4,﹣2);(2)答案见解析;(3)6.
【分析】(1)根据点P、P1的坐标确定出平移规律,再求出A1、B1、C1的坐标即可;
(2)根据网格结构找出点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可;
(3)利用△AOA1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
【详解】解:(1)∵点P(a,b)的对应点为P1(a+6,b﹣2),∴平移规律为向右6个单位,向下2个单位,∴A(﹣3,3),B(﹣5,1),C(﹣2,0)的对应点的坐标为A1(3,1),B1(1,﹣1),C1(4,﹣2);
故答案为:A1 (3,1)B1 (1,-1)C1(4,﹣2);
(2)△A1B1C1如图所示;
(3)△AOA1的面积=6×3﹣×3×3﹣×3×1﹣×6×2=18﹣﹣﹣6=18﹣12=6.
【点睛】本题考查了利用平移变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.
2.在同一平面内,若一个点到一条直线的距离不大于1,则称这个点是该直线的“伴侣点”.
在平面直角坐标系中,已知点M(1,0),过点M作直线l平行于y轴,点A(﹣1,a),点B(b,2a),点 C(﹣,a﹣1),将三角形ABC进行平移,平移后点A的对应点为D,点B的对应点为E,点C的对应点为F.
(1)试判断点A是否是直线l的“伴侣点”?请说明理由;
(2)若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且三角形MFD的面积为,试判断点B是否是直线l的“伴侣点”?请说明理由.
【答案】(1)点A不是直线l的“伴侣点”;(2)点B是直线l的“伴侣点”,理由详见解析.
【分析】(1)直线l:x=1,求出点A到直线l的距离为2,根据“伴侣点”的定义进行判定即可.
(2)从点C到点F,找出平移规律,进而求得点D,E的坐标,根据点E落在x轴上,且三角形MFD的面积为,即可求出的值,即可求出点B的坐标,根据“伴侣点”的定义进行判定即可.
【详解】(1)∵A(﹣1,a),直线l:x=1,
∴点A到直线l的距离为2,2>1,
∴点A不是直线l的“伴侣点”.
(2)∵→F(1,a+b),
∴横坐标加,纵坐标加b+1,
∴
∵点E落在x轴上,
∴2a+b+1=0,
∵三角形MFD的面积为,
∴
∴
当时,解得,此时点是直线l的“伴侣点”.
当时,此时点B是直线l的“伴侣点”.
【点睛】属于新定义问题,考查点到直线的距离,点的平移,三角形的面积公式等,读懂题目中“伴侣点”的定义是解题的关键.
3.如图,在平面直角坐标系中,点A,B的坐标分别为A(0,3),B(6,3),现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
(1)求点C,D的坐标;
(2)点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为秒,问:是否存在这样的使得四边形OMDB的面积为12?若存在,请求出的值,若不存在,请说明理由.
(3)在(2)的条件下,点M从O点出发的同时,点N从D点出发,以每秒2个单位的速度向左平移运动,当点N到达点O时运动停止.设射线BN交轴于点E.设运动时间为秒,问:的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
【答案】(1)C(-2,0),D(4,0)
(2)t=2
(3)值不变,为6
【分析】(1)根据点的坐标及平移方法即可确定;
(2)过B作BH⊥OD的延长线,垂足为H.由(1)中点的坐标得出D=6,DH=2,OD=4,AB=6,设M点坐标为(0,t),连接MB、OB,则四边形的面积等于△OBD的面积加上△OMD的面积等于12,然后解出t即可;
(3)设运动时间为秒,OM=t,ON=4-2t(0≤t≤2),过B作BH⊥OD的延长线,垂足为H,连接MB,OB,结合图形可得=S△ONB+S△OMB,然后代入求解即可.
【详解】(1)解:∵点A,B的坐标分别为A(0,3),B(6,3),将点A,B分别向下平移3个单位,再向左平移2个单位
∴C(-2,0),D(4,0);
(2)解:存在;如图,过B作BH⊥OD的延长线,垂足为H.
由题意得点C和点D的坐标分别为(-2,0)和(4,0).A(0,3),B(6,3),
∴CD=6,DH=2,OD=4,AB=6,
设M点坐标为(0,t),连接MB、OB,
∴OM=t.
∵S四边形OMBD=S△OBD+S△OMB=12,
∴,
即,
解得t=2;
(3)解:不变.
理由如下:
如图所示,设运动时间为秒,OM=t,ON=4-2t(0≤t≤2),
过B作BH⊥OD的延长线,垂足为H,连接MB,OB,
∵=S四边形OMBN,S四边形OMBN=S△ONB+S△OMB,
∴=S△ONB+S△OMB
=
=
=6-3t+3t
=6;
∴为定值6,故其值不会变化.
【点睛】本题属于四边形的综合问题,考查了点坐标平移、坐标与图形、动点问题以及图形的面积等知识点,灵活应用所学知识是解答本题的关键.
4.如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系点A(0,a),C(b,0)满足.D为线段AC的中点.在平面直角坐标系中以任意两点P(x 1,y1)、Q(x2,y2)为端点的线段中点坐标为,.
(1)则A点的坐标为 ;点C的坐标为 .D点的坐标为 .
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点 Q 到 达 A 点 整 个 运 动 随 之 结 束 . 设 运 动 时 间 为 t (t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ,若存在,请求出t的值;若不存在,请说明理由.
(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,的值是否会发生变化?若不变,请求出它的值,若变化请说明理由.
【答案】(1)(0,4),(2,0),(1,2);(2)1,理由见解析;(3)2,理由见解析
【分析】(1)根据绝对值和算术平方根的非负性,求得a,b的值,再利用中点坐标公式即可得出答案;
(2)先得出CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,再根据S△ODP=S△ODQ,列出关于t的方程,求得t的值即可;
(3)过H点作AC的平行线,交x轴于P,先判定OG∥AC,再根据角的和差关系以及平行线的性质,得出∠PHO=∠GOF=∠1+∠2,∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,最后代入进行计算即可.
【详解】解:(1)∵.
∴a﹣2b=0,b﹣2=0,
解得a=4,b=2,
∴A(0,4),C(2,0);
∴x==1,y==2,
∴D(1,2).
故答案为(0,4),(2,0),(1,2).
(2)如图1中,
由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,
∴0<t≤2时,点Q在线段AO上,
即 CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,
∴S△DOP=OP•yD=(2﹣t)×2=2﹣t,S△DOQ=OQ•xD=×2t×1=t,
∵S△ODP=S△ODQ,
∴2﹣t=t,
∴t=1;
(3)的值不变,其值为2.理由如下:如图2中,
∵∠2+∠3=90°,
又∵∠1=∠2,∠3=∠FCO,
∴∠GOC+∠ACO=180°,
∴OG∥AC,
∴∠1=∠CAO,
∴∠OEC=∠CAO+∠4=∠1+∠4,
如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,
∴∠PHO=∠GOF=∠1+∠2,
∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,
∴=,
=,
=2.
【点睛】本题考查三角形综合题、非负数的性质、三角形的面积、平行线的性质等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题.
5.如图所示,在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是,,,先将向上平移3个单位长度,再向右平移2个单位长度,得到.
(1)在图中画出.
(2)写出点的坐标.
(3)若轴上有一点,使与面积相等,求出点的坐标.
【答案】(1)见解析;(2),,;(3)P点的坐标为或.
【分析】(1)分别确定平移后的对应点 再顺次连接即可得到答案;
(2)根据在坐标系内的位置直接写出坐标即可;
(3)先求解再设,根据 可得的上的高为:,再利用三角形的面积公式列方程,解方程可得答案.
【详解】解:(1)如图,是所求作的三角形,
(2)由图可得:,,
(3)
设,而
的上的高为:,
或
或
的坐标为或.
【点睛】本题考查的是平移的作图,坐标与图形,坐标系内三角形的面积,熟练掌握平面直角坐标系及点的坐标是解题的关键.
6.在如图所示的直角坐标系中,△ABC的顶点坐标分别是A(﹣2,5),B(﹣4,﹣1)C(2,3),△A1B1C1是由△ABC平移得到,点P(x1,y1)是△ABC内一点,经过平移点P(x1,y1)变成点P1(x1+2,y1﹣1)
(1)写出三个顶点的坐标
(2)请画出平移后的△A1B1C1
(3)求△A1B1C1的面积
【答案】(1)A1(0,4)、B1(−2,−2)、C1(4,2)
(2)见解析
(3)14
【分析】(1)由题意知,将三个顶点分别向右平移2个单位,向下平移1个单位得到其对应点, 即可得出答案;
(2)将(1)中三个点的坐标描出,再首尾顺次连接即可;
(3)用矩形的面积减去四周三个三角形的面积.
(1)
∵点P(x1,y1)是△ABC内一点,经过平移点P(x1,y1)变成点P1(x1+2,y1﹣1),
∴可以由向右平移2个单位,再向下平移1个单位得到,则A1(0,4)、B1(−2,−2)、C1(4,2);
(2)
分别描出A1(0,4)、B1(−2,−2)、C1(4,2)三个点,顺次连接这三个点,则得到平移后的△A1B1C1,如图所示:
(3)
=36−4−6−12
=14.
【点睛】本题主要考查作图—平移变换,解题的关键是确定平移变换.
7.如图1,在平面直角坐标系中,点是坐标原点,边长为2的正方形(点与点重合)和边长为4的正方形的边和都在轴上,且点坐标为.正方形以3个单位长度/秒的速度沿轴向右运动,记正方形和正方形重叠部分的面积为,假设运动时间为秒,且.
(1)点的坐标为______;
(2)如图2,正方形向右运动的同时,动点在线段上以1个单位长度/秒的速度从到运动.连接,.
①为何值时,所在直线垂直于轴?
②为何值时,?
【答案】(1);(2)①,②或
【分析】(1)根据直角坐标系的特点和正方形的性质求解即可;
(2)①根据所在直线垂直于轴.得出方程求解即可;
②分两种情况,当时和当时,利用面积公式解答即可.
【详解】解:(1)由正方形EFGH的边长为4,H(7,0),可以得到F的坐标为(3,4);
(2)①要使所在直线垂直于轴.只需要,则,解得.
∴当时,所在直线垂直于轴.
②由题意,知,.
当时,.
∴当时,点与点重合;时,点与点重合;
时,点与点重合;当时,点与点重合,;
当时,点与点重合,.
分以下两种情况讨论:
情况一:当时,如图3,,,,
∵,∴,即.
解得;
情况二:当时,如图4,,,,
∵,∴,
即,解得.
图4
情况三:当时,,
∴
.
不合题意,舍去.
综上所述,当或时,.
【点睛】本题主要考查了坐标与图形,正方形的性质与面积公式,解题的关键在于能够熟练掌握相关知识进行求解.
8.如图,在平面直角坐标系中,已知△ABC中,点A坐标为(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)写出点C的坐标( , )
(2)在y轴上是否存在点P,使得S△POB=S△ABC,若存在,求出点P的坐标;若不存在;
(3)把点C往上平移3个单位得到点H,画射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探索∠BMA、∠HBM、∠MAC之间的数量关系,并证明你的结论.
【答案】(1)-2,0;(2)存在,(0,6)或(0,-6);(3)∠BMA=∠MAC+∠MBH或∠MAC=∠BMA+∠HBM,证明见解析
【分析】(1)根据坐标轴上,两点间的距离的计算方法,即可得出结论;
(2)先求出△ABC的面积,进而求出△BOP的面积,最后用三角形的面积公式,建立方程,求解,即可得出结论;
(3)先判断出BH∥x轴,再分两种情况,利用平行线的性质和三角形的外角的性质,即得出结论.
【详解】解:(1),,
,
故答案为:-2,0;
(2)如图1,,,
,
,
,
设,
,
,
,
或;
(3)∠BMA=∠MAC+∠MBH或∠MAC=∠BMA+∠HBM.
证明:由平移知,H(-2,3),
∵B(2,3),
∴BH∥x轴,
①当点M在线段CH上时,如图2,
过点M作MG∥x轴,
∴∠AMG=∠MAC,
∵BH∥x轴,MG∥x轴,
∴BH∥MG,
∴∠BMG=∠HBM,
∴∠BMA=∠AMG+∠BMG=∠MAC+∠MBH;
②当点M在CH的延长线上时,如图3,
记AM与BH的交点为N,
∵BH∥x轴,
∴∠MNH=∠MAC,
∵∠MNH是△BMN的外角,
∴∠MNH=∠BMA+∠HBM,
∴∠MAC=∠BMA+∠HBM,
即∠BMA=∠MAC+∠MAC或∠MAC=∠BMA+∠HBM.
【点睛】此题是几何变换综合题,主要考查了平移的性质,三角形的面积公式,平行线的性质,三角形的外角的性质,作出辅助线是解本题的关键.
9.在如图所示的平面直角坐标系中,A(2,3),B(4,0).
(1)将线段AB沿x轴向左平移4个单位长度,再沿y轴向上平移2个单位长度至线段CD(C与A对应),求△ABD的面积;
(2)将线段AB平移至线段PQ(P与B对应),且点P恰好落在y轴上.
①若△ABQ的面积为3,请通过计算说明,线段AB是如何平移至线段PQ的?
②设P(0,y),且-8≤y≤8,请用含y的式子表示△ABP的面积,并求出当y=-8时,△ABP的最大面积.
【答案】(1)面积为4;(2)①向左平移4个单位,向上平移3个或9个单位得到;②S=6-y,当y=-8时,S最大=14.
【分析】(1)根据平移的规律,画出图形,用割补法依据S△ABD=S△ABO+S△AOD-S△OBD
求三角形的面积即可.
(2)①根据平移的规律,画出图形,设点Q的坐标为(-2,y),分两种情况讨论:用y表示出S△ABQ=9-y.或S△ABQ=y-9.即可求出y,再根据Q与C对应即可找到平移规律.
②分P点在y轴的正半轴和负半轴,根据三角形面积求法,即可用含y的式子表示△ABP的面积,然后把y代入即可求出.
【详解】解:(1)如图1:∵A(2,3),B(4,0).将线段AB沿x轴向左平移4个单位长度,再沿y轴向上平移2个单位长度.
∴C(-2,5),D(0,2).
连接OA,∴OD=2,OB=4.
S△ABD=S△ABO+S△AOD-S△OBD
S△ABD==4.
(2)①将线段AB平移至线段PQ(P与B对应),且点P恰好落在y轴上.则线段AB向左平移4个单位,设Q点坐标为(-2,y),∵△ABQ的面积为3,故点P在Q的上方,
Ⅰ.如图2(1):
作QH垂直x轴,连接HA,∴OP=,OB=4.
S△ABQ=S△ABH+S△AQH-S△QHB
S△ABQ==9-y
若△ABQ的面积为3,则9-y=3,
解得:y=6,
即Q为(-2,6),
∵将线段AB平移至线段PQ,Q点(-2,6)与A点(2,3)对应.
故将线段AB沿x轴向左平移4个单位长度,再沿y轴向上平移3个单位长度至线段PQ(B与P对应),
Ⅱ..如图2(2):
作QH垂直x轴,连接HA,∴OP=,OB=4.
S△ABQ=S△ABH+S△AQH-S△QHB
∴S△ABD==y-9,
依题意得:y-9=3,∴y=12,
∵将线段AB平移至线段PQ,Q点(-2,12)与A点(2,3)对应.
故将线段AB沿x轴向左平移4个单位长度,再沿y轴向上平移9个单位长度至线段PQ(B与P对应),
故若△ABQ的面积为3,将线段AB沿x轴向左平移4个单位长度,再沿y轴向上平移3个(或9个)单位长度至线段PQ(B与P对应).
②Ⅰ.当P在y的正半轴,如图:设P点坐标为(0,y),
连接OA,∴OP=,OB=4.
S△ABP=S△ABO+S△APO-S△OBP
S△ABD==6-y.
Ⅱ当P在y轴的负半轴上时,如图4:
,
∵y<0.
∴S△ABP=S△ABO+S△APO-S△OBP
S△ABD==6-y.
∴S△ABD=6-y,
当y=-8时,S△ABD=14.
【点睛】本题考查了三角形综合题型,涉及到了点的平移变换、三角形的面积、坐标与图形的性质等知识点,能求出符合的所有情况是解此题的关键,用了分类讨论和数形结合的数学思想.
10.如图,在平面直角坐标系中,已知,,将线段平移至,点在轴正半轴上(不与点重合),连接,,,.
(1)写出点的坐标;
(2)当的面积是的面积的3倍时,求点的坐标;
(3)设,,,判断、、之间的数量关系,并说明理由.
【答案】(1);(2)①若点在线段上,;②若点在线段延长线上,;(3)①若点在线段上,;②若点在线段延长线上,,见解析.
【分析】(1)过C点作CF⊥y轴与点F,过B点作BE⊥x轴与点E,根据平移的性质可得OA=BC,OF=BE,进而得到C点坐标;
(2)分点在线段上和点在线段延长线上两种情况进行讨论,与的高都是一样的,所以只要底边符合条件即可;
(3)分点在线段上和点在线段延长线上两种情况进行讨论,过点作,利用平行线的性质进行证明即可.
【详解】解:(1)如图1,过C点作CF⊥y轴与点F,过B点作BE⊥x轴与点E,
∵,,
∴,,
∴;
(2)设,
①若点在线段上,
∵,
∴,
∴,
∴
②若点在线段延长线上,
∵,
∴,
∴,
∴;
(3)如图2、3,过点作,
由平移的性质知,
∴,
∴,(两直线平行,内错角相等),
①若点在线段上,(图2)
,
即;
②若点在线段延长线上,(图3)
,
即
【点睛】本题主要考查坐标与图形变化-平移,三角形的面积公式,平行线的性质,属于综合题,解此题的关键在于作适当的辅助线,分情况进行讨论.
11.如图,在正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为、.
(1)请在如图所示的网格平面内画出平面直角坐标系;
(2)点是边BC上任意一点,三角形经过平移后得到,点P的对应点为.
①直接写出点的坐标 ;
②画出平移后的.
(3)在y轴上是否存在点P,使的面积等于面积的,若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)见解析;(2)①;②见解析;(3)存在,或.
【分析】(1)根据A、C的坐标分别为、先确定原点O,即可画图;
(2)①根据的对应点确定平移方向和距离,即可求解;
②根据平移的方向和距离确定A、B、C的对应点,然后连线即可;
(3)再网格图中利用割补法先求得的面积,然后根据题意即可求解.
【详解】
解:(1)如图所示;
(2)①∵,
∴先向右平移6格,再向下平移2格,得到
∵
∴,
故答案是:(4,-1);
②如图所示;
(3)
∴
∴
当点P在O点上方时:;
当点P在O点下方时:.
【点睛】此题主要考查平移的性质,正确理解平移中,点的坐标变化特点是解题关键.
12.如图,在正方形网格中,每个小正方形的边长为1个单位长度,格点(顶点是网格的交点的三角形)的顶点A,C坐标分别为,
(1)请在如图所示的网格内画出对应的平面直角坐标系;
(2)再把先向右平移5个单位长度,再向下平移3个单位长度得到,且点的对应点分别为,请你在图中画出;
(3)在Y轴上是否存在点P,使的面积等于的面积的一半,若存在求出点P的坐标;若不存在说明理由.
【答案】(1)见解析;(2)见解析;(3)存在,点P的坐标为(0,8)或(0,-2)
【分析】(1)依据点A,C坐标分别为(-4,5),(0,3)即可得到原点的位置,进而得出直角坐标系;
(2)依据平移的方向和距离,即可得到△A′B′C′;
(3)y轴上存在点P,依据△PBC的面积等于△ABC的面积的一半,列出方程即可得到点P的纵坐标的值.
【详解】解:(1)平面直角坐标系如图所示;
(2)如图所示,△A′B′C′即为所求;
(3)△ABC的面积为4×4-×2×4-×2×1-×4×3=5,
y轴上存在点P,使△PBC的面积等于△ABC的面积的一半,
设P(0,y),则CP=|y-3|,
×|y-3|×1=×5,
解得y=8或-2,
∴点P的坐标为(0,8)或(0,-2).
【点睛】本题考查作图-平移变换,三角形的面积等知识,解题的关键是熟练掌握平移变换的性质.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
人教版七年级数学下册常考点微专题提分精练 开学收心考试模拟卷02(原卷版+解析): 这是一份人教版七年级数学下册常考点微专题提分精练 开学收心考试模拟卷02(原卷版+解析),共16页。试卷主要包含了若与是同类项,则、的值分别是,如果,那么下列结论一定成立的是,下列计算结果相等的为,下列说法等内容,欢迎下载使用。
人教版七年级数学下册常考点微专题提分精练 开学收心考试模拟卷01(原卷版+解析): 这是一份人教版七年级数学下册常考点微专题提分精练 开学收心考试模拟卷01(原卷版+解析),共16页。试卷主要包含了向东行驶,记作,向西行驶记作,化简得,下列方程中,是一元一次方程的是,解方程时,去分母正确的是等内容,欢迎下载使用。
专题14 网格中画相似-【微专题】2022-2023学年九年级数学下册常考点微专题提分精练(人教版): 这是一份专题14 网格中画相似-【微专题】2022-2023学年九年级数学下册常考点微专题提分精练(人教版),文件包含专题14网格中画相似原卷版docx、专题14网格中画相似解析版docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。













