2024年中考数学压轴题专项练习—阿基米德折弦定理

这是一份2024年中考数学压轴题专项练习—阿基米德折弦定理，文件包含62阿基米德折弦定理docx、62阿基米德折弦定理答案docx等2份试卷配套教学资源，其中试卷共43页， 欢迎下载使用。

1、以专题复习为主。如选择题、填空题的专项练习，要把握准确度和时间的安排。加强对二次函数与几何图形结合的综合性试题、实际应用题等专题的练习，深化对常考题型的熟悉程度。在函数复习过程中，如果考生未能完全理解简单实例中的数量关系和变化规律，针对此类问题，在专项复习中，可以通过选择题、填空题的专项练习，进行突破，如“读懂图象信息问题”等，将复杂问题由浅入深，层层分解，提高分析和判断能力。
2、重视方法思维的训练。对初中数学所涉及的函数思想、方程思想、数形结合思想、分类讨论思想、转化与化归思想、整体思想等数学思想方法，要通过典型试题的训练，进一步渗透和深刻理解其内涵，重要处舍得投入时间与精力。强化解题过程中常用的配方法、待定系数法等通法。
3、拓宽思维的广度，培养多角度、多维度思考问题的习惯。将专项复习中的共性习题串连起来，通过一题多解，积极地探求解决问题的最优解法，这样，对于解决难度较大的压轴题会有很大的帮助。

阿基米德折弦定理
1．（2022•成都自主招生）在中，顺次连接、、．
（1）如图1，若点是的中点，且交延长线于点，求证：为的切线；
（2）如图2，在（1）的条件下，连接，过点作于点，若，，，则、、有何数量关系？
（3）如图3，当时，是延长线上一点，是线段上一点，且，若，的周长为9，请求出的值？
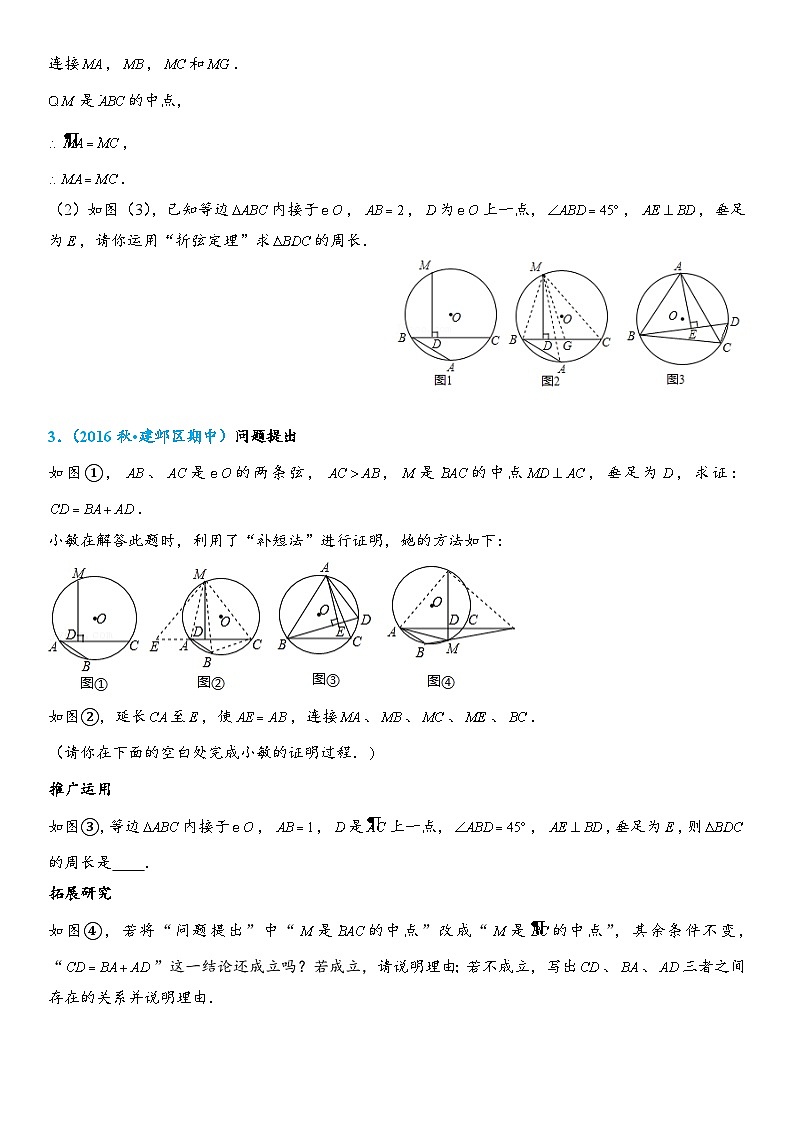
2．（2019秋•丰泽区校级期末）古希腊数学家阿基米德提出并证明了“折弦定理”．如图1，和是的两条弦（即折线是圆的一条折弦），，是优弧的中点，则从向所作垂线的垂足是折弦的中点，即．
（1）请按照下面的证明思路，写出该证明的剩余部分；
证明：如图2，在上截取，
连接，，和．
是的中点，
，
．
（2）如图（3），已知等边内接于，，为上一点，，，垂足为，请你运用“折弦定理”求的周长．
3．（2016秋•建邺区期中）问题提出
如图①，、是的两条弦，，是的中点，垂足为，求证：．
小敏在解答此题时，利用了“补短法”进行证明，她的方法如下：
如图②，延长至，使，连接、、、、．
（请你在下面的空白处完成小敏的证明过程．
推广运用
如图③，等边内接于，，是上一点，，，垂足为，则的周长是 ．
拓展研究
如图④，若将“问题提出”中“是的中点”改成“是的中点”，其余条件不变，“”这一结论还成立吗？若成立，请说明理由；若不成立，写出、、三者之间存在的关系并说明理由．
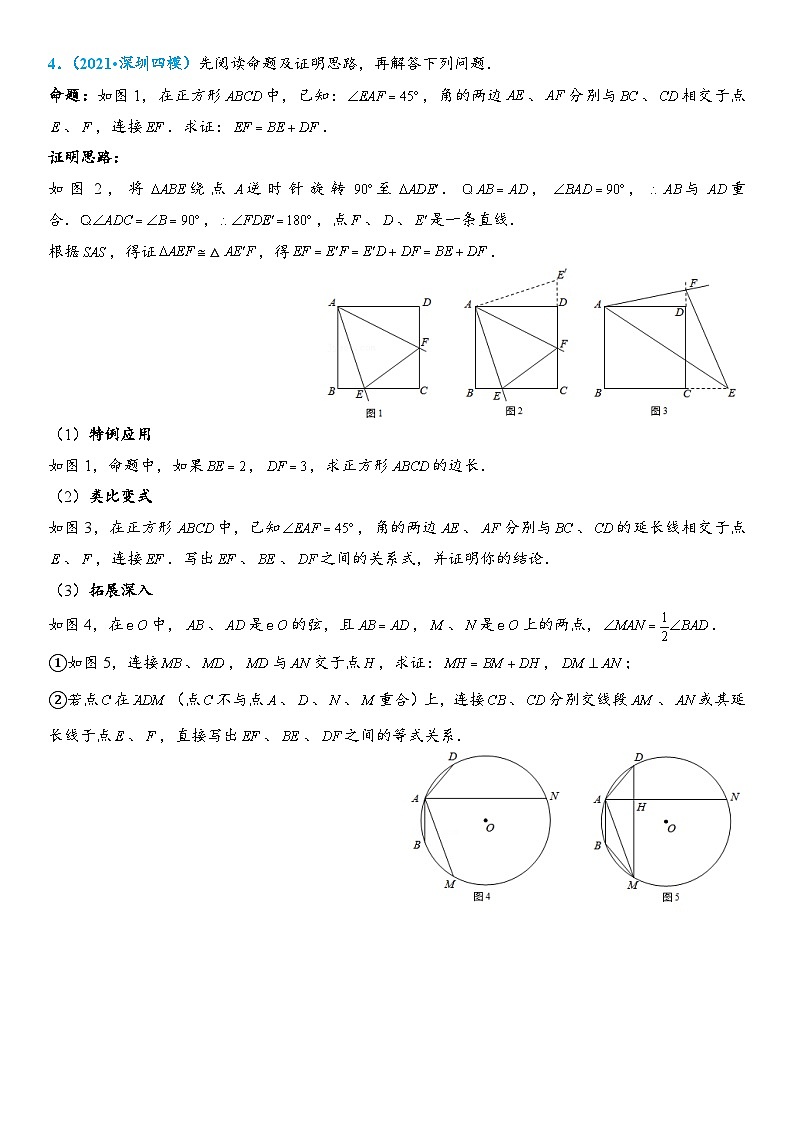
4．（2021•深圳四模）先阅读命题及证明思路，再解答下列问题．
命题：如图1，在正方形中，已知：，角的两边、分别与、相交于点、，连接．求证：．
证明思路：
如图2，将绕点逆时针旋转至．，，与重合．，，点、、是一条直线．
根据，得证△，得．
（1）特例应用
如图1，命题中，如果，，求正方形的边长．
（2）类比变式
如图3，在正方形中，已知，角的两边、分别与、的延长线相交于点、，连接．写出、、之间的关系式，并证明你的结论．
（3）拓展深入
如图4，在中，、是的弦，且，、是上的两点，．
①如图5，连接、，与交于点，求证：，；
②若点在（点不与点、、、重合）上，连接、分别交线段、或其延长线于点、，直接写出、、之间的等式关系．
5．（2012秋•厦门期末）已知、、、是上的四点，，是四边形的对角线
（1）如图1，连接，若，求证：是的平分线；
（2）如图2，过点作，垂足为，若，，求线段的长度．
6．（2012•咸宁模拟）小明学习了垂径定理，做了下面的探究，请根据题目要求帮小明完成探究．
（1）更换定理的题设和结论可以得到许多真命题．如图1，在中，是劣弧的中点，直线于点，则．请证明此结论；
（2）从圆上任意一点出发的两条弦所组成的折线，成为该圆的一条折弦．如图2，，组成的一条折弦．是劣弧的中点，直线于点，则．可以通过延长、相交于点，再连接证明结论成立．请写出证明过程；
（3）如图3，．组成的一条折弦，若是优弧的中点，直线于点，则，与之间存在怎样的数量关系？写出结论，不必证明．
7．如图，已知、、、四点顺次在上，且，于，
求证：．
8．（2023•东港区校级一模）如图：已知点、、、顺次在圆上，，，垂足为．证明：．（阿基米德折弦定理）
9．（2023•海口一模）【问题呈现】阿基米德折弦定理：阿基米德，公元前公元前212年，古希腊）是有史以来最伟大的数学家之一，他与牛顿、高斯并称为三大数学王子．如图1，和是的两条弦（即折线是圆的一条折弦），，点是的中点，则从向所作垂线的垂足是折弦的中点，即．下面是运用“截长法”证明的部分证明过程．
证明：如图2，在上截取，连接、、和．
是的中点，
，
又，，
，
，
又，
，
即．
【理解运用】如图1，、是的两条弦，，，点是的中点，于点，则 ；
【变式探究】如图3，若点是的中点，【问题呈现】中的其他条件不变，判断、、之间存在怎样的数量关系？并加以证明．
【实践应用】如图4，是的直径，点圆上一定点，点圆上一动点，且满足，若，的半径为5，则 ．
10．（2019•六合区模拟）我们知道，如图1，是的弦，点是的中点，过点作于点，易得点是的中点，即．上一点，则折线称为的一条“折弦”．
（1）当点在弦的上方时（如图，过点作于点，求证：点是“折弦”的中点，即．
（2）当点在弦的下方时（如图，其他条件不变，则上述结论是否仍然成立？若成立说明理由；若不成立，那么、、满足怎样的数量关系？直接写出，不必证明．
（3）如图4，已知中，，，的外接圆的半径为2，过上一点作于点，交于点，当时，求的长．
11．（2021秋•海州区校级期中）某数学活动小组在一次活动中，对一个数学问题作如下探究：
【问题发现】如图1，，为的两条弦，点为的中点，过作，垂足为．
求证：．
【问题探究】小明同学的思路是：如图2，在上截取，连接，，，．
请你按照小明的思路完成上述问题的证明过程．
【结论运用】如图3，是的内接等边三角形，点是上一点，，连接，，过点作，垂足为．若，则的周长为 ．
【变式探究】如图4，若将【问题发现】中“点为的中点”改为“点为优弧的中点”，其他条件不变，上述结论“”还成立吗？若成立，请说明理由；若不成立，请写出、、之间的新等量关系，并加以证明．
12．（2018•深圳）如图，内接于，，，点为上的动点，且．
（1）求的长度；
（2）在点的运动过程中，弦的延长线交延长线于点，问的值是否变化？若不变，请求出的值；若变化，请说明理由；
（3）在点的运动过程中，过点作，求证：．
13．（2011•鄂州自主招生）如图，点、、、四点顺次在上，，于，小华对此进行了研究：首先，他取为正三角形，且为的直径，计算后发现：；接着，他取为等腰直角三角形，平分，试问：还成立吗？小华利用这种情形还计算出，请问他的结论正确吗？另外，小华还猜想：一般地，恒成立，请你帮助他证明或否定这个结论．
（对于前面两问只需作出肯定或否定的回答，无需证明）
14．（2020•青羊区校级三模）如图所示，在中，，，点为劣弧上的动点，且．
（1）求的长度；
（2）求的值；
（3）过点作，求证：．
15．（2018秋•海淀区校级月考）问题呈现：阿基米德折弦定理：如图1，和是的两条弦（即折线是圆的一条折弦），，是的中点，则从向所作垂线的垂足是折弦的中点，即．下面是运用“截长法”证明的部分证明过程．
证明：如图2，在上截取，连接，，和．
是的中点，
请按照上面的证明思路，写出该证明的剩余部分；
实践应用：
（1）如图3，已知内接于，，是的中点，依据阿基米德折弦定理可得图中某三条线段的等量关系为 ．
（2）如图4，已知等腰内接于，，为上一点，连接，，于点，的周长为，，请求出的长．
16．如图，已知圆内接中，，为的中点，于，求证：．