2024年中考数学压轴题专项练习—垂径定理

这是一份2024年中考数学压轴题专项练习—垂径定理，文件包含57垂径定理答案docx、57垂径定理docx等2份试卷配套教学资源，其中试卷共81页， 欢迎下载使用。
1、以专题复习为主。如选择题、填空题的专项练习，要把握准确度和时间的安排。加强对二次函数与几何图形结合的综合性试题、实际应用题等专题的练习，深化对常考题型的熟悉程度。在函数复习过程中，如果考生未能完全理解简单实例中的数量关系和变化规律，针对此类问题，在专项复习中，可以通过选择题、填空题的专项练习，进行突破，如“读懂图象信息问题”等，将复杂问题由浅入深，层层分解，提高分析和判断能力。
2、重视方法思维的训练。对初中数学所涉及的函数思想、方程思想、数形结合思想、分类讨论思想、转化与化归思想、整体思想等数学思想方法，要通过典型试题的训练，进一步渗透和深刻理解其内涵，重要处舍得投入时间与精力。强化解题过程中常用的配方法、待定系数法等通法。
3、拓宽思维的广度，培养多角度、多维度思考问题的习惯。将专项复习中的共性习题串连起来，通过一题多解，积极地探求解决问题的最优解法，这样，对于解决难度较大的压轴题会有很大的帮助。

垂径定理
1．（2023•南岗区二模）圆内接，是圆的切线，点为切点，．
（1）如图1，连接，求证：；
（2）如图2，当为直径，点在弧上，连接、、时；求证：．
（3）如图3，在（2）的条件下，连接与交于点，连延长与交于点，，，求的长．
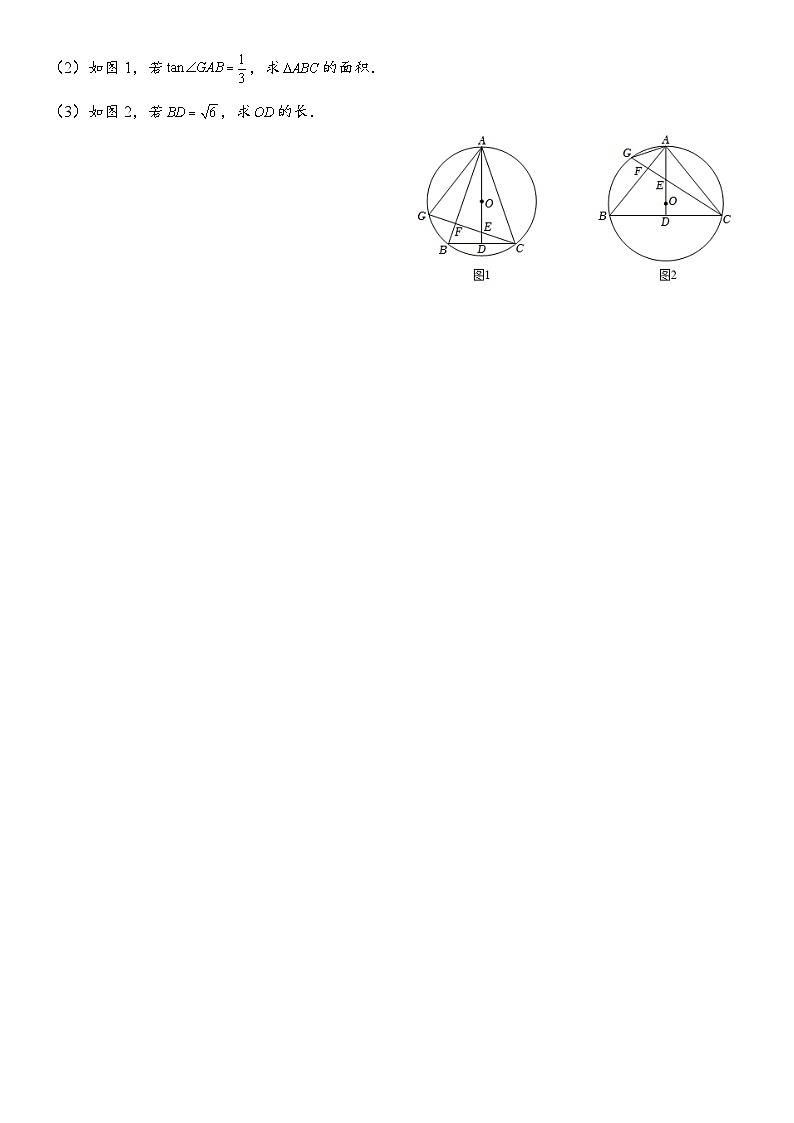
2．（2022•镇海区校级二模）如图，为等腰三角形的外接圆，，延长交于点，过点作垂直交于点，交于点，交于点，连结，若．
（1）求证：．
（2）如图1，若，求的面积．
（3）如图2，若，求的长．
3．（2022秋•香坊区校级月考）在中，弦、相交于点，且．
（1）如图1，求证：；
（2）如图2，点、分别为弦、的中点，连接、，且，求证：；
（3）如图3，在（2）的条件下，连接、，交于点，过点作交于点，，，求的长．
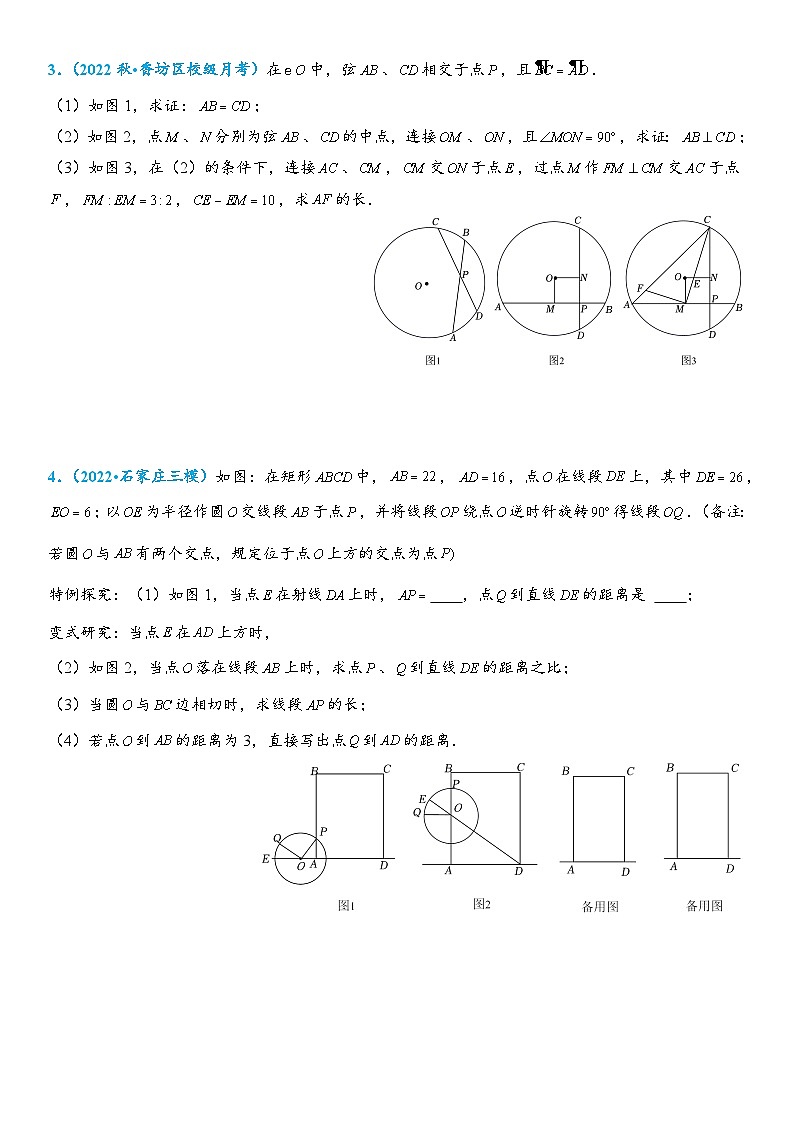
4．（2022•石家庄三模）如图：在矩形中，，，点在线段上，其中，；以为半径作圆交线段于点，并将线段绕点逆时针旋转得线段．（备注：若圆与有两个交点，规定位于点上方的交点为点
特例探究：（1）如图1，当点在射线上时， ，点到直线的距离是 ；
变式研究：当点在上方时，
（2）如图2，当点落在线段上时，求点、到直线的距离之比；
（3）当圆与边相切时，求线段的长；
（4）若点到的距离为3，直接写出点到的距离．
5．（2022春•南岗区校级月考）如图1，是的直径，点在上，是弧的中点，连接、
（1）求证：；
（2）如图2，过点作于，交于点，连接交于点，求证：；
（3）如图3，在（2）的条件下，延长交于点，交于点，连接交于点，连接、，若，的面积是，求弦的长．
6．（2010•深圳）如图1所示，以点为圆心的圆与轴，轴分别交于点，，，，直线与相切于点，交轴于点，交轴于点．
（1）请直接写出，的半径，的长；
（2）如图2所示，弦交轴于点，且，求的值；
（3）如图3所示，点为线段上一动点（不与，重合），连接交于点，弦交轴于点．是否存在一个常数，始终满足，如果存在，请求出的值；如果不存在，请说明理由．
7．内接于，点在上，连接，交边于点，且．
（1）如图1，求证：；
（2）如图2，点在上，连接，交弦于点，交边于点，连接，交边于点，若，求证：；
（3）如图3，在（2）的条件下，当点在边上时，连接，交边于点，点在线段上，连接并延长，交于点，连接、，若，，，求弦的长．
8．（2023•南岗区一模）已知内接于，是直径，过点作的切线．
（1）如图1，求证：；
（2）如图2，当是弧的中点时，过点作于．求证：；
（3）如图3，在（2）的条件下，与相交于点，连接、与相交于点，若的面积为12，，求点到的距离．
9．（2023•永嘉县校级二模）如图，在矩形中，，点，，分别在边，，上，，，于点，为的外接圆的圆心，于点，设，．
（1）求的长．
（2）求关于的函数表达式．
（3）在边上取点，使，连结．
①当为直角三角形时，求所有满足条件的的值．
②当点关于的对称点恰好落在边上时，连结，求的值．
10．（2023•道外区三模）已知四边形内接于，是的直径，在，连接．
（1）如图1，求证：；
（2）如图2，连接，过点作，垂足为点，交于点，求证：；
（3）如图3，在（2）的条件下，过点作的切线交的延长线于点，连接，若，，求的半径长．
11．（2023•鼓楼区校级一模）如图，是的直径，弦于点，点在上，恰好经过圆心，连接．
（1）若，，求的半径；
（2）若，，求的长．
12．（2023•晋安区校级模拟）已知如图1，在中，弦于点，，，．是的中点．
（1）求的长．
（2）求的长．
（3）如图2，若，连接交于点，试说明的度数是否会发生变化，若不变请求出的度数，并说明理由．
13．（2023•涪城区模拟）如图，已知：在中，，点是边上的动点，交于，以为直径的分别交，于点，．
（1）求证：．
（2）若，．
①当，求的长．
②当为等腰三角形时，请求出所有满足条件的的腰长．
（3）若，且，，在一条直线上，则与的比值为 ．
14．（2023•鄞州区校级一模）如图，为的直径，弦于点，为劣弧上一动点，与的延长线交于点，连接、、、．为常数，且．
（1）求证：；
（2）求的值（用含的式子表示）；
（3）设，．
①求与的数量关系；
②当，且时，求的值．
15．（2023•隆回县一模）如图，是的直径，是的弦，点是延长线的一点，平分交于点，过点作，垂足为点．
（1）猜想直线与有怎样的位置关系？并证明你的猜想；
（2）若，，求的半径和的长．
16．（2023•宁津县一模）【概念引入】
在一个圆中，圆心到该圆的任意一条弦的距离，叫做这条弦的弦心距．
【概念理解】
（1）如图1，在中，半径是5，弦，则这条弦的弦心距长为 ．
（2）通过大量的做题探究；小明发现：在同一个圆中，如果两条弦相等，那么这两条弦的弦心距也相等．但是小明想证明时却遇到了麻烦．请结合图2帮助小明完成证明过程如图2，在中，，，，求证：．
【概念应用】如图3，在中，的直径为20，且弦垂直于弦于，请应用上面得出的结论求的长．
17．（2023•南岗区校级一模）如图，为圆的直径，为弦，为圆的切线，过点作，垂足为，交于点．
（1）如图1，求证：；
（2）如图2，连接，若，过点作，垂足为，求证：；
（3）如图3，在（2）的条件下，延长交圆于点，连接、，与交于点，若平分，，求的长．
18．（2023•平房区一模）已知内接于，连接．
（1）如图1，求证：；
（2）如图2，为上一点，连接并延长交于点，且，为上一点，连接、，若，求证：；
（3）如图3，在（2）的条件下，连接、，连接并延长交于点，交于点，若为中点，，求的长．
19．（2023•新城区校级一模）综合与实践
【问题提出】
（1）如图①，点为上一点，点为外一点，（点、点在直线的同侧），则与的大小关系为： （填“”、“ ”、“ ” ．
【问题探究】
（2）如图②，已知线段，点为上一点，且，，过点作直线于点，经过、两点的恰好与相切于点，连接、，求．
【问题解决】
（3）我们把摄像头拍摄某一线段时，拍摄视角最大时拍摄点的位置称为“鹰眼点”，此时视角的余弦值称为“鹰眼值”．
如图③，在四边形中，为一个导轨，为一段铁轨，，．米，米，米，摄像头从点出发沿导轨滑动拍摄铁轨，求摄像头到达“鹰眼点”时的移动距离及“鹰眼值” ．
20．（2023•西安二模）【问题提出】
（1）如图①，在等腰直角中，，为等边三角形，，则线段的长为 ．
【问题解决】
（2）如图②，在等腰直角中，，，以为直径作半圆，点为上一动点，求点、之间的最大距离；
【问题探究】
（3）一次手工制作课程中，老师要求小明和小丽组制作一种特殊的部件，部件的要求如图③，部件是由直角以及弓形组成，其中，，，，点为的中点，，这时候小明和小丽在讨论这个部件，其中小丽说点到的最大距离是点、之间的距离，小明说不对，你认为谁的说法正确？请说明理由，并求出点到的最大距离．
21．（2022秋•自贡期末）在平面直角坐标系中，的半径为，是与圆心不重合的点，点关于的限距点的定义如下：若为直线与的一个交点，满足，则称为点关于的限距点，如图1为点及其关于的限距点的示意图．
（1）当的半径为时．
①分别判断点，，关于的限距点是否存在？若存在，求其坐标；
②如图2，点的坐标为，，分别切于点，，点在的边上．若点关于的限距点存在，求点的横坐标的取值范围．
（2）保持（1）中，，三点不变，点在的边，上沿的方向运动，的圆心的坐标为，半径为，若点关于的限距点不存在，则的取值范围为 ．
22．（2022秋•江都区月考）在半径为5的中，是直径，点是直径上方半圆上一动点，连接、．
（1）如图1，则面积的最大值是 ；
（2）如图2，如果，①则 ；②作的平分线交于点，求长的长．
（3）如图3，连接并保持平分，为线段的中点，过点作，在点运动过程中，请直接写出长的最大值．
23．（2022•德州）如图1，在等腰三角形中，，为底边的中点，过点作，垂足为，以点为圆心，为半径作圆，交于点，．
（1）与的位置关系为 ；
（2）求证：是的切线；
（3）如图2，连接，，，求的直径．（结果保留小数点后一位．参考数据：，，
24．（2022•绵阳）如图，为的直径，为圆上的一点，为劣弧的中点，过点作的切线与的延长线交于点，与的延长线交于点，与交于点．
（1）求证：；
（2）若的半径为，，求的长度；
（3）在（2）的条件下，求的面积．
25．（2022•德阳）如图，是的直径，是的弦，，垂足是点，过点作直线分别与，的延长线交于点，，且．
（1）求证：是的切线；
（2）如果，，
①求的长；
②求的面积．