2024年中考数学压轴题专项练习—垂美四边形模型

这是一份2024年中考数学压轴题专项练习—垂美四边形模型，文件包含49垂美四边形模型答案docx、49垂美四边形模型docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。
1、以专题复习为主。如选择题、填空题的专项练习，要把握准确度和时间的安排。加强对二次函数与几何图形结合的综合性试题、实际应用题等专题的练习，深化对常考题型的熟悉程度。在函数复习过程中，如果考生未能完全理解简单实例中的数量关系和变化规律，针对此类问题，在专项复习中，可以通过选择题、填空题的专项练习，进行突破，如“读懂图象信息问题”等，将复杂问题由浅入深，层层分解，提高分析和判断能力。
2、重视方法思维的训练。对初中数学所涉及的函数思想、方程思想、数形结合思想、分类讨论思想、转化与化归思想、整体思想等数学思想方法，要通过典型试题的训练，进一步渗透和深刻理解其内涵，重要处舍得投入时间与精力。强化解题过程中常用的配方法、待定系数法等通法。
3、拓宽思维的广度，培养多角度、多维度思考问题的习惯。将专项复习中的共性习题串连起来，通过一题多解，积极地探求解决问题的最优解法，这样，对于解决难度较大的压轴题会有很大的帮助。
垂美四边形模型
1．（2023春•青川县期末）概念理解：对角线互相垂直的四边形叫做垂美四边形
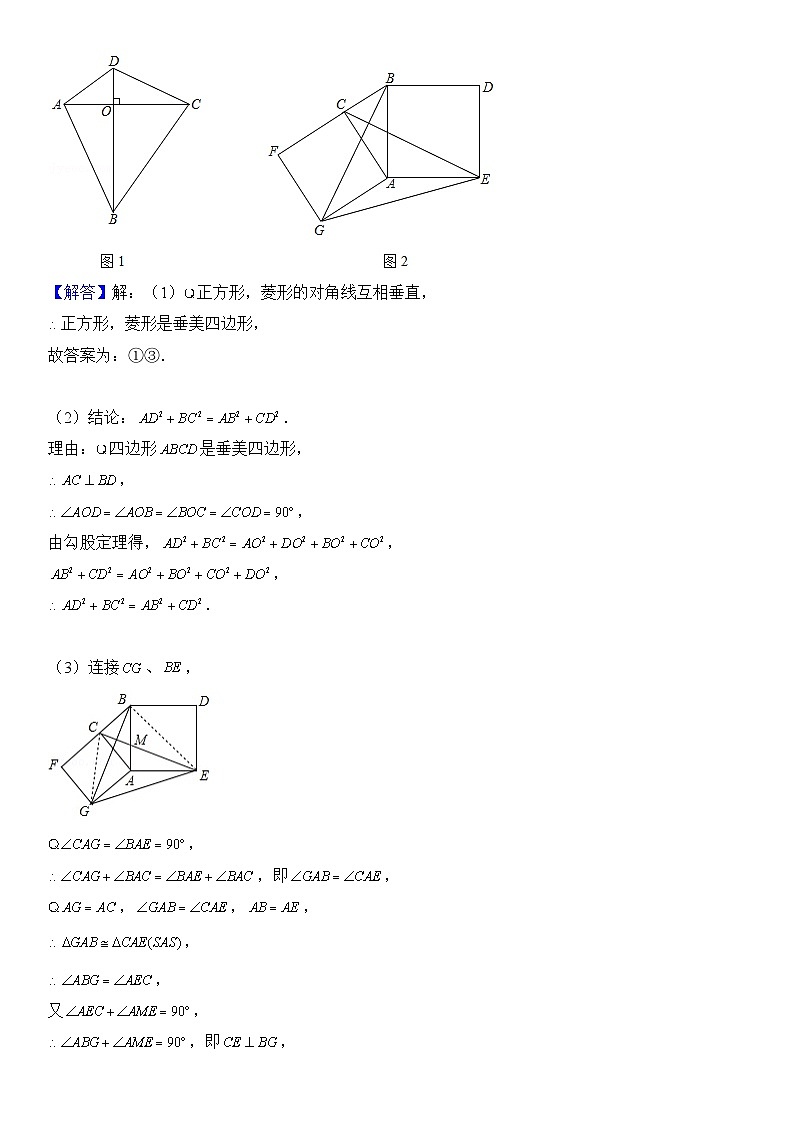
（1）性质探究：如图1，四边形是垂美四边形，直接写出、、、的数量关系： ．
（2）解决问题：如图2，分别以的直角边和斜边为边向外作正方形和正方形，连接、、．若，，求的长（可直接利用（1）中性质）
2．（2021春•祁阳县期末）如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：在下列四边形中，①正方形；②矩形；③菱形；④平行四边形．是垂美四边形的是： （填写序号）；
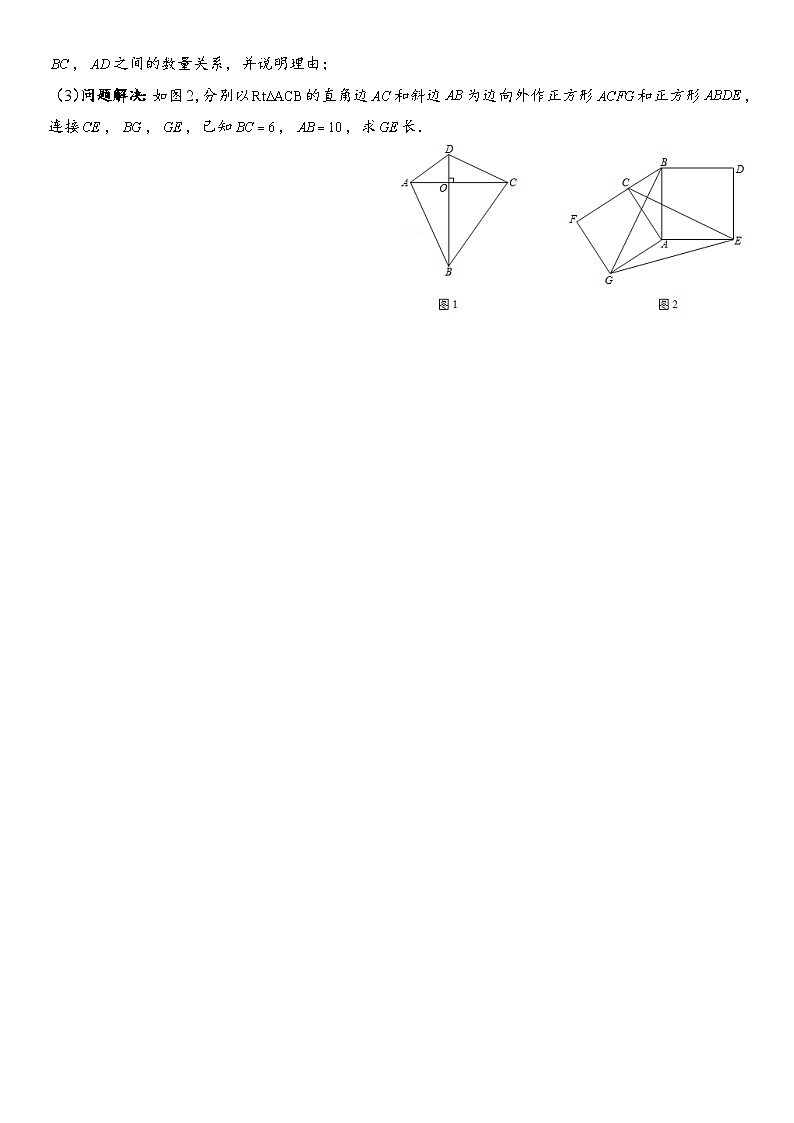
（2）性质探究：如图1，垂美四边形中，，垂足为，试猜想：两组对边，与，之间的数量关系，并说明理由；
（3）问题解决：如图2，分别以的直角边和斜边为边向外作正方形和正方形，连接，，，已知，，求长．
3．（2023春•怀宁县期末）小明学习了平行四边形这一章后，对特殊四边形的探究产生了兴趣，发现另外一类特殊四边形，如图1，我们把两条对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：在平行四边形、矩形、菱形、正方形中，一定是垂美四边形的是 ．
（2）性质探究：通过探究，直接写出垂直四边形的面积与两对角线，之间的数量关系： ．
（3）问题解决：如图2，分别以的直角边和斜边为边向外作正方形和正方形，连接，，，已知，．
①求证：四边形为垂美四边形；
②求出四边形的面积．
4．（2023春•孝南区期中）新定义：对角线互相垂直的四边形叫做“垂美四边形”．
（1）如图1，已知四边形是垂美四边形．
①若，则它的面积为 ；
②若，，，，探究、、、的数量关系．
（2）如图2，已知、分别是中边、的中点，，，，请运用②中的结论，直接写出的长为 ．
5．（2023春•德城区校级月考）如图，我把对角线互相垂直的四边形叫做“垂美四边形”．
（1）性质探究：如图1，已知四边形中，，垂足为，求证：．
（2）解决问题：已知，，分别以的边和向外作等腰和等腰．如图2，当，连接，求．
6．（2022春•海安市月考）如图1，我们把对角线相互垂直的四边形叫做垂美四边形．
（1）概念理解：在四边形中，以下是垂美四边形的是 ．
①平行四边形；②矩形；③菱形；④，．
（2）性质探究：小美同学猜想“垂美四边形两组对边的平方和相等”，即，如图1，在四边形中，若，则．请判断小美同学的猜想是否正确，并说明理由．
（3）问题解决：如图2．在中，，，、分别是、的中点，连接、．有，求．
7．（2021春•郧阳区期中）认识新知：对角线互相垂直的四边形叫做“垂美四边形”．
（1）概念理解：如图1，在四边形中，已知，当与满足 时，四边形为“垂美四边形”（直接写结果）；
（2）性质探究：如图2，四边形的对角线、交于点，且．求证：；
（3）解决问题：如图3，分别以的直角边和斜边向外作等腰和等腰，连结，已知，，则 （直接写出结果）．
8．（2021春•红谷滩区校级期末）定义：我们把对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：如图2，在四边形中，，，问四边形是垂美四边形吗？请说明理由．
（2）性质探究：
①如图1，垂美四边形两组对边，与，之间有怎样的数量关系．写出你的猜想，并给出证明；
②如图3，在中，点为斜边的中点，分别以，为底边，在外部作等腰三角形和等腰三角形，连接，，分别交，于点，．试猜想四边形的形状，并说明理由；
（3）问题解决：
如图4，分别以的直角边和斜边为边向外作正方形和正方形，连接，，，已知，．求的长．
9．（2023春•雁塔区校级期末）如图1，对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：如图2，在四边形中，，，问四边形是垂美四边形吗？请说明理由．
（2）性质探究：如图1，试探索垂美四边形两组对边、与、之间的数量关系并说明理由．
（3）问题解决：如图3，分别以的直角边和斜边为边向外作等腰直角三角形和等腰直角三角形，使得，，，连接，，，已知，，求的值．
10．（2021•南明区模拟）如图，我把对角线互相垂直的四边形叫做“垂美四边形”．
（1）性质探究：如图1．已知四边形中，，垂足为，求证：．
（2）解决问题：已知，，分别以的边和向外作等腰和等腰．
①如图2，当，连接，求；
②如图3，当，点、分别是、中点连接．若，则 ．