2024年中考数学压轴题专项练习—等腰三角形中的半角模型

这是一份2024年中考数学压轴题专项练习—等腰三角形中的半角模型，文件包含45等腰三角形中的半角模型答案docx、45等腰三角形中的半角模型docx等2份试卷配套教学资源，其中试卷共49页， 欢迎下载使用。

1、以专题复习为主。如选择题、填空题的专项练习，要把握准确度和时间的安排。加强对二次函数与几何图形结合的综合性试题、实际应用题等专题的练习，深化对常考题型的熟悉程度。在函数复习过程中，如果考生未能完全理解简单实例中的数量关系和变化规律，针对此类问题，在专项复习中，可以通过选择题、填空题的专项练习，进行突破，如“读懂图象信息问题”等，将复杂问题由浅入深，层层分解，提高分析和判断能力。
2、重视方法思维的训练。对初中数学所涉及的函数思想、方程思想、数形结合思想、分类讨论思想、转化与化归思想、整体思想等数学思想方法，要通过典型试题的训练，进一步渗透和深刻理解其内涵，重要处舍得投入时间与精力。强化解题过程中常用的配方法、待定系数法等通法。
3、拓宽思维的广度，培养多角度、多维度思考问题的习惯。将专项复习中的共性习题串连起来，通过一题多解，积极地探求解决问题的最优解法，这样，对于解决难度较大的压轴题会有很大的帮助。
等腰三角形中的半角模型
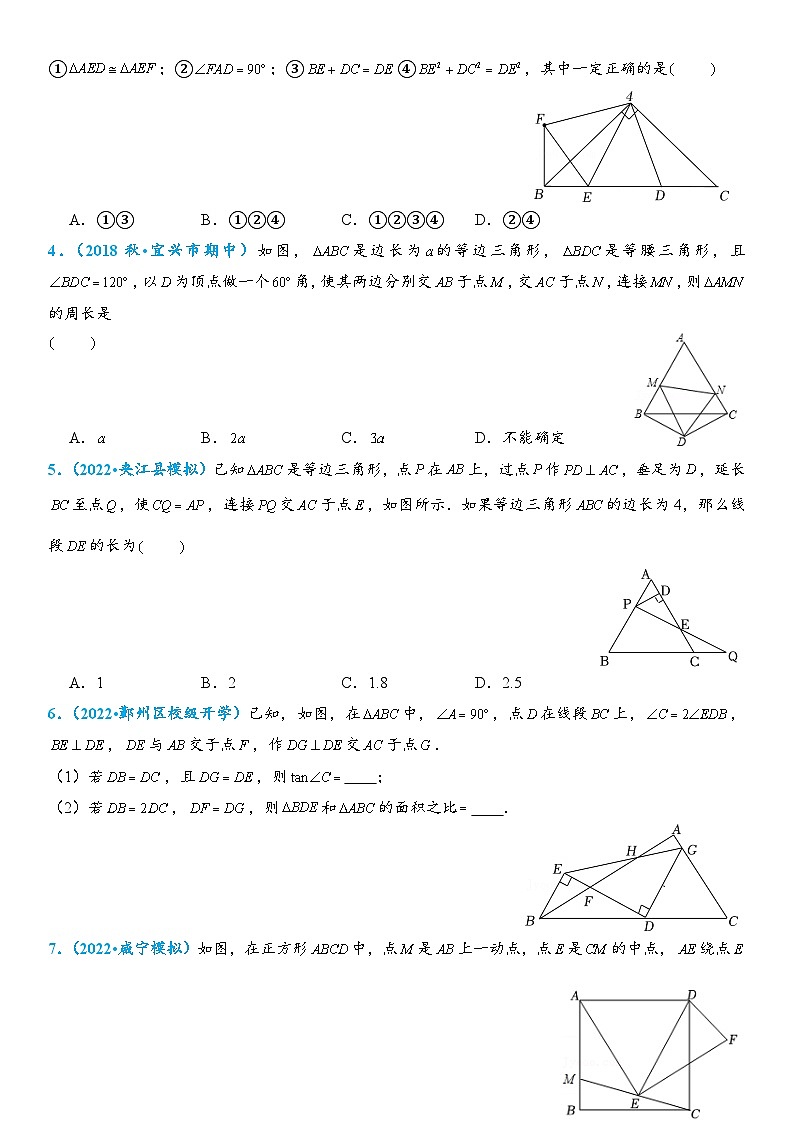
1．（2021秋•渝中区校级期末）如图，中，，，、为边上两点，，过点作，且，连接、．下列结论：①，②平分；③若，，则；④若，，其中正确的个数有
A．1个B．2个C．3个D．4个
2．（2021秋•郧阳区期中）如图，在等腰中，，，点是线段上一点，，点是延长线上一点，点是线段上一点，，下面的结论：①；②；③；④，其中正确的个数有
A．1个B．2个C．3个D．4个
3．（2021春•牡丹区期中）如图，在中，，、是斜边上两点，且，将绕点顺时针旋转后，得到，连接，下列结论：
①；②；③④，其中一定正确的是
A．①③B．①②④C．①②③④D．②④
4．（2018秋•宜兴市期中）如图，是边长为的等边三角形，是等腰三角形，且，以为顶点做一个角，使其两边分别交于点，交于点，连接，则的周长是

A．B．C．D．不能确定
5．（2022•夹江县模拟）已知是等边三角形，点在上，过点作，垂足为，延长至点，使，连接交于点，如图所示．如果等边三角形的边长为4，那么线段的长为
A．1B．2C．1.8D．2.5
6．（2022•鄞州区校级开学）已知，如图，在中，，点在线段上，，，与交于点，作交于点．
（1）若，且，则 ；
（2）若，，则和的面积之比 ．
7．（2022•咸宁模拟）如图，在正方形中，点是上一动点，点是的中点，绕点顺时针旋转得到，连接，．给出结论：①；②；③； ④若正方形的边长为2，则点在射线上运动时，有最小值．其中结论正确的是 （把你认为正确结论的序号都填上）．
8．（2023•大连模拟）综合与实践
问题情境：数学活动课上，王老师出示了一个问题：如图1，在中，点在边上，于交于，．求证．
独立思考：（1）请解答王师提出的问题．
实践探究：（2）在原有问题条件不变的情况下，王老师增加下面条件，并提出新问题，请你解答．“如图2，作于点，若，探究线段与之间的数量关系，并证明．”
问题解析：（3）数学活动小组同学对上述问题进行特殊化研究之后发现，当点与点重合时，连接，若给出的值，则可求出的值．该小组提出下面的问题，请你解答．”
如图3，在（2）的条件下，当点与点重合时，连接，若，求的长”．
9．（2021秋•牡丹江期末）已知，等边与顶点重合，将等边绕顶点顺时针旋转，边所在直线与的边相交于点，并在边上截取，连接．
（1）将等边旋转至如图①所示位置时，求证：；
（2）将等边顺时针旋转至如图②、图③位置时，请分别直接写出，，之间的数量关系，不需要证明；
（3）在（1）和（2）的条件下，若，，则 ．
10．（2021秋•桦甸市期末）如图，是等边三角形，是边上一点（点不与点，重合），作，使角的两边分别交边，于点，，且．
（1）如图①，若，则 度；
（2）如图②，是边上一点（点不与点，重合），求证：；
（3）如图③，若是边的中点，且，则四边形的周长为 ．
11．（2021春•嘉定区期末）在等边三角形的两边、所在直线上分别有两点、，为外一点，且，，．探究：当点、分别在直线、上移动时，，，之间的数量关系．
（1）如图①，当点、在边、上，且时，试说明．
（2）如图②，当点、在边、上，且时，还成立吗？
答： ．（请在空格内填“一定成立”“不一定成立”或“一定不成立” ．
（3）如图③，当点、分别在边、的延长线上时，请直接写出，，之间的数量关系．
12．（2021秋•连山区期中）如图，中，，，点在边上运动不与、重合），点在线段上，连结，．点运动时，始终满足．
（1）当的最小值为4时，此时 ；
（2）当时，判断的形状并说明理由；
（3）在点的运动过程中，的形状是等腰三角形时，请直接写出此时的度数．
13．（2021秋•连山区期中）如图1，等边三角形和等边三角形，连接，．其中．
（1）求证：；
（2）如图2，当点、、在一条直线上时，交于点，交于点，求证：；
（3）利用备用图补全图形，直线，交于点，连接，若，，直接写出的长．
14．（2017春•杨浦区校级期末）在等边的两边、所在直线上分别有两点、，为外一点，且，，．探究：当、分别在直线、上移动时，、、之间的数量关系及的周长与等边的周长的关系．
（1）如图1，是周长为9的等边三角形，则的周长 ；
（2）如图2，当点、边、上，且时，、、之间的数量关系是 ；此时 ；
（3）点、在边、上，且当时，猜想（2）问的两个结论还成立吗？写出你的猜想并加以证明．
15．（2021秋•温江区校级期中）如图，在中，．
（1）如图1，若，，求的面积；
（2）如图2，为外的一点，连接，且，，过点作交的延长线于点，求证：；
（3）如图3，在（2）的条件下，作平分交于点，过点作交的延长线于点，点为直线上点的一个动点，连接，过点作，且始终满足，连接，若，请求出取得最小值时的值．
16．（2017•宛城区一模）（1）问题背景：
如图①，在四边形中，，，，，分别是、上的点，且．探究图中线段，，之间的数量关系．
小明同学探究此问题的方法是，延长到点，使，连接，先证明，再证明，可得出结论，他的结论应是 ；
（2）探索延伸：
如图②，若在四边形中，，．，分别是，上的点，且，上述结论是否仍然成立，请说明理由；
（3）实际应用：
如图③，在某次军事演习中，舰艇甲在指挥中心北偏西的处，舰艇乙在指挥中心南偏东的处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里小时的速度前进，舰艇乙沿北偏东的方向以80海里小时的速度前进，2小时后，指挥中心观测到甲、乙两舰艇分别到达，处，当时，两舰艇之间的距离是 海里．
（4）能力提高：
如图④，等腰直角三角形中，，，点，在边上，且．若，，则的长为 ．
17．（2015•杭州模拟）（1）如图1，菱形中，，点，分别在边，上，，连接，作，使与关于直线对称，连接． 求证：；
（2）如图2，等腰中，，，点，在边上，在的左边，且，若，，求的长．
18．（2021秋•内江期末）旋转变换是解决数学问题中一种重要的思想方法，通过旋转变换可以将分散的条件集中到一起，从而方便解决问题．已知，中，，，点、在边上，且．
（1）如图，当时，将绕点顺时针旋转到的位置，连结．
① ；②求证：；
（2）如图，当时，猜想、、的数量关系，并说明理由．
19．（2020秋•西青区期末）已知在中，，，是边上的点，将绕点旋转，得到，连接．
（1）如图1，当，时，求证：；
（2）如图2，当时，请写出与的数量关系，并说明理由．
（3）当，，时，请直接写出与的数量关系（不必说明理由）．
20．（2014秋•新乡期末）阅读下面材料：
小辉遇到这样一个问题：如图1，在中，，，点，在边上，．若，，求的长．
小辉发现，将绕点按逆时针方向旋转，得到，连接（如图，由图形旋转的性质和等腰直角三角形的性质以及，可证，得．解，可求得（即的长．
请回答：在图2中，的度数是 ，的长为 ．
参考小辉思考问题的方法，解决问题：
如图3，在四边形中，，．，分别是边，上的点，且．猜想线段，，之间的数量关系并说明理由．
3804