2024年中考数学压轴题专项练习—风筝模型

这是一份2024年中考数学压轴题专项练习—风筝模型，文件包含39风筝模型答案docx、39风筝模型docx等2份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。

1、以专题复习为主。如选择题、填空题的专项练习，要把握准确度和时间的安排。加强对二次函数与几何图形结合的综合性试题、实际应用题等专题的练习，深化对常考题型的熟悉程度。在函数复习过程中，如果考生未能完全理解简单实例中的数量关系和变化规律，针对此类问题，在专项复习中，可以通过选择题、填空题的专项练习，进行突破，如“读懂图象信息问题”等，将复杂问题由浅入深，层层分解，提高分析和判断能力。
2、重视方法思维的训练。对初中数学所涉及的函数思想、方程思想、数形结合思想、分类讨论思想、转化与化归思想、整体思想等数学思想方法，要通过典型试题的训练，进一步渗透和深刻理解其内涵，重要处舍得投入时间与精力。强化解题过程中常用的配方法、待定系数法等通法。
3、拓宽思维的广度，培养多角度、多维度思考问题的习惯。将专项复习中的共性习题串连起来，通过一题多解，积极地探求解决问题的最优解法，这样，对于解决难度较大的压轴题会有很大的帮助。

风筝模型
1．（2017春•西城区校级期中）（1）如图1，设，则 ；
（2）把三角形纸片顶角沿折叠，点落到点处，记为，为．
①如图2，，与的数量关系是 ；
②如图3，请你写出，与的数量关系，并说明理由．
（3）如图4，把一个三角形纸片的三个顶角分别向内折叠之后，3个顶点不重合，那么图中 ．
【解答】解：（1）；
故答案为：；
（2）①如图2，猜想：，理由是：
由折叠得：，，
，
，
；
故答案为：；
②如图3，，理由是：
，，
，
，
，
；
（3）如图4，由题意知，
又，，，
，
．
故答案为：．
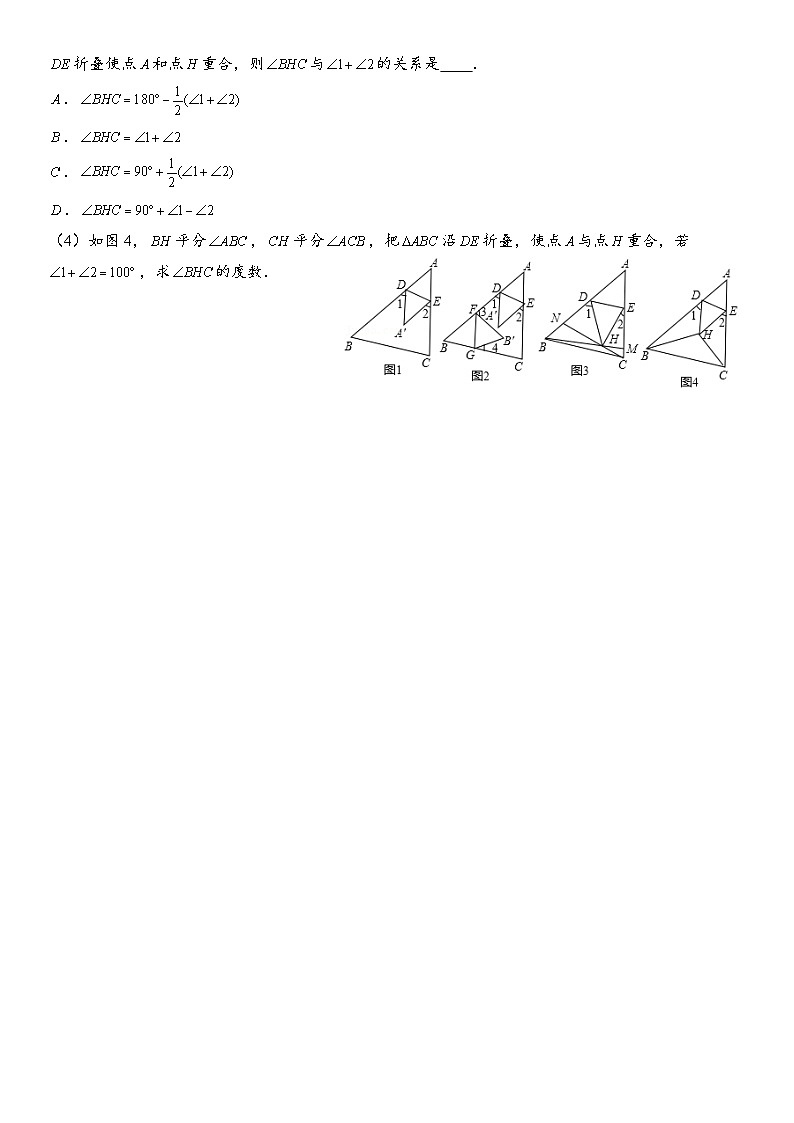
2．（2017春•铜山区期中）（1）如图1，把沿折叠，使点落在点处，请直接写出与的关系： ．
（2）如图2，把分别沿、折叠，使点落在点处，使点落在点处，若，则
（3）如图3，在锐角中，于点，于点，、交于点，把沿折叠使点和点重合，则与的关系是 ．
．
．
．
．
（4）如图4，平分，平分，把沿折叠，使点与点重合，若，求的度数．
【解答】解：（1）；
理由如下：由折叠的性质得：，，
①，
又，
②，
由①②得：；
故答案为：；
（2）由（1）可得，，，
，
，
故答案为：；
（3）理由：，，
，，
，由（1）知．
．
．
故选；
（4）由（1）得：，
得，
，
平分，平分，
，
．
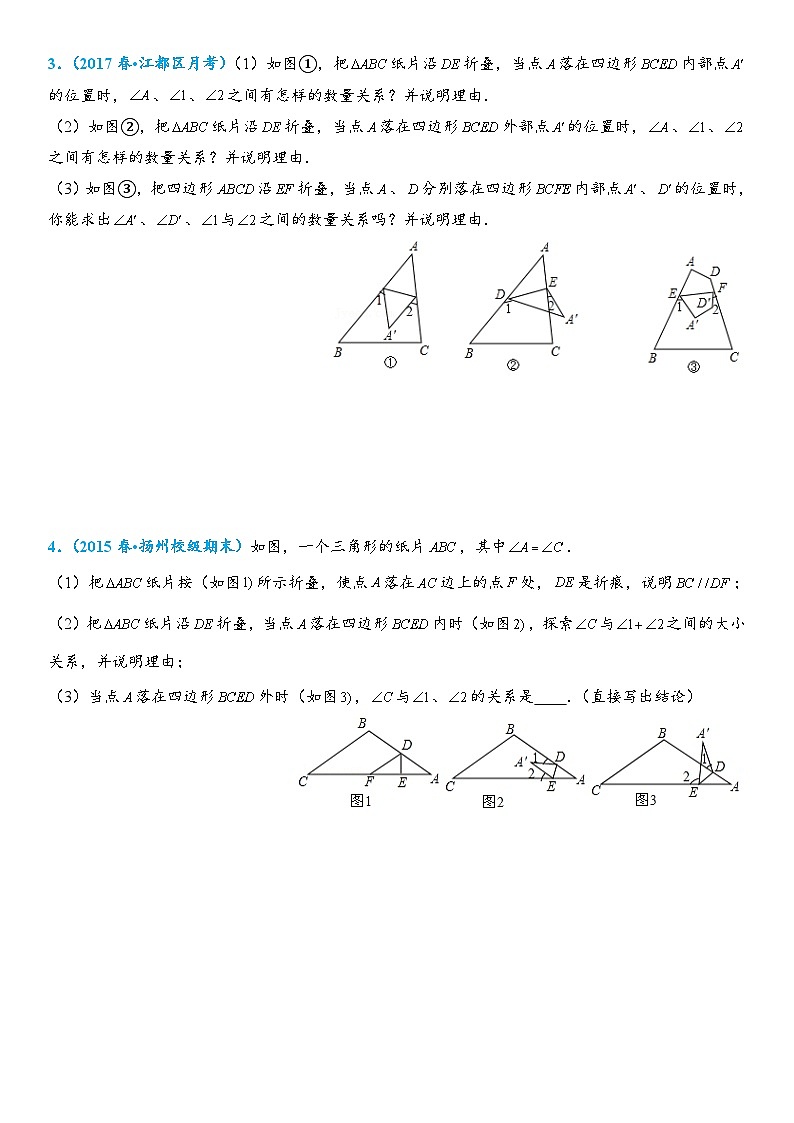
3．（2017春•江都区月考）（1）如图①，把纸片沿折叠，当点落在四边形内部点的位置时，、、之间有怎样的数量关系？并说明理由．
（2）如图②，把纸片沿折叠，当点落在四边形外部点的位置时，、、之间有怎样的数量关系？并说明理由．
（3）如图③，把四边形沿折叠，当点、分别落在四边形内部点、的位置时，你能求出、、与之间的数量关系吗？并说明理由．
【解答】解：（1）如图，根据翻折的性质，，，
，
，
整理得，；
（2）根据翻折的性质，，，
，
，
整理得，；
（3）根据翻折的性质，，，
，
，
整理得，．
4．（2015春•扬州校级期末）如图，一个三角形的纸片，其中．
（1）把纸片按（如图所示折叠，使点落在边上的点处，是折痕，说明；
（2）把纸片沿折叠，当点落在四边形内时（如图，探索与之间的大小关系，并说明理由；
（3）当点落在四边形外时（如图，与、的关系是 ．（直接写出结论）
【解答】解：（1）根据折叠的性质得：，
，
，
；
（2），
理由：四边形的内角和等于，
．
又，
．
又，
，
，
；
（3），
证明如下：由题意得：（设为，（设为；
，
，
；
，
，
，
．
故答案为：．
5．（2015春•宜兴市校级月考）操作：折叠纸片，并将折叠后的部分压平在纸片原来所在平面内．
研究一：
（1）将纸片沿直线折叠成图1的形状，则、与之间的数量关系为 （不需要说明理由）．
（2）将纸片沿直线折成图2的形状，则、和之间存在怎样的数量关系？请试着找出来，并说明理由．
研究二：将四边形与不平行）沿直线折叠成图3的形状，则、与、之间的数量关系是 （请将含、的项放在等式的左边，其余各项放在等式的右边），并说明理由．
【解答】解：（1）如图1，
由图形折叠的性质可知，①，②，
①②得，
即，
故；
（2）．
证明如下：
如图2，
连接构造等腰三角形，
，，
得，
（3）如图③，
由图形折叠的性质可知，，
两式相加得，
即，
所以，．
6．（2013春•姜堰市期中），直线交于，交于，将沿折叠，使落在同一平面上的处，的两边与、的夹角分别记为，
如图①，当落在四边形内部时，探索与之间的数量关系，并说明理由．
如图②，当落在下方时，请直接写出与之间的数量关系．
如图③，当落在右侧时，探索与，之间的数量关系，并说明理由．
【解答】解：（1）．理由如下：
如图①，，
又，
，
又，
；
（2）．
理由：，
又，
，
又，
；
（3）．理由如下：
如图③，设交于点．
，，
，
，
△是由沿直线折叠而得，
，
．
7．（2021秋•永春县期中）如图1，在中，，，点在线段上（不与点、点重合），以为腰作等腰直角，于点．
（1）求证：；
（2）连接交于点，猜想与的数量关系并证明；
（3）如图2，过点作交的延长线于点，过点作交于点，连接，当点在线段上运动时（不与点，点重合），请说明始终成立．
【解答】（1）证明：为等腰三角形，，是等腰直角三角形，于．
，，，
，
在和中，
，
；
；
（2）解：结论：．
理由：，
，
，
．
在和中，
，
，
，
，，，
，
；
（3）证明：过作交于点，如图2所示：
，，，
，，
，
为等腰直角三角形，
，
在和中，
，
，
，，
，，
，
在和中，
，
，
，
．
8．（2017春•丰县校级月考）如图1，将纸片沿折叠，使点落在处的位置．
（1）如果点落在四边形内部（如图，、、之间有怎样的数量关系？并说明理由．
（2）如果点落在四边形的边上，则与之间的数量关系是 ．
（3）如果点落在四边形外部（如图，、、之间有怎样的数量关系？并说明理由．
【解答】解：（1），
理由：延折叠和重合，
，，
，
，
；
（2），如图3，
，
故答案为：；
（3），
理由：延折叠和重合，
，
，，
，
即．
9．（2010春•洪山区期末）如图：将纸片沿折叠成图①，此时点落在四边形内部，则与、之间有一种数量关系保持不变，请找出这种数量关系并说明理由．
（1）若折成图②或图③，即点落在或上时，分别写出与；与之间的关系；（不必证明）
（2）若折成图④，写出与、之间的关系式；（不必证明）
（3）若折成图⑤，写出与、之间的关系式．（不必证明）
【解答】解：延长、，交于点；
则即为折叠前的三角形，
由折叠的性质知：．
图①中：连接；
由三角形的外角性质知：
，；
则，
即．
图②中：由三角形的外角性质知：
，
即．
图③中：，解法同图②．
图④中：由三角形的外角性质，知：
，，
即，故．
图⑤中：，解法同图④．
故当点落在四边形内部，．
（1）图②中，；图③中，．
（2）图④中，．
（3）图⑤中，．
10．（2023春•抚顺月考）如图，中，，为中点，点在边上（点不与点，重合），连接，过点作交于点，连接．
（1）求证：
（2）若，，，直接写出线段的长．
【解答】证明：（1）延长至使，连接，
为中点，
，
在与中，
，
，
，，
，
，
连接，
，，
，
在中，
，
即：；
解：（2）设，
，，，
则，
，
，
，
即：，
由（1）知：，，，
，，
，
，
即：，
解得：，
即：．
11．（2023春•襄汾县期末）如图，在中，，比大．点是线段上任意一点，点、分别在线段、上．将折叠，点落在点处，点落在点处，折痕分别为和，点、都在射线上．
（1） ， ， ．
（2）如图1，当点、都落在的延长线上时，与有什么数量关系？请说明理由．
（3）如图2，当点落在线段上，点落在的延长线时，请直接写出与的数量关系．
【解答】（1），，
，
，
，
，
；
故答案为：，，；
（2）由折叠可得：，，
，，
，
，，
，
（3）由折叠可得：，，
，，
，，
，
．
12．（2016秋•赣州期中）将纸片沿折叠使点落在处的位置．
（1）如果落在四边形的内部（如图，与之间存在怎样的数量关系？并说明理由．
（2）如果落在四边形的边上，这时图1中的变为角，则与之间的关系是 ．
（3）如果落在四边形的外部（如图，这时与、之间又存在怎样的数量关系？并说明理由．
【解答】解：（1）图1中，，
理由是：延折叠和重合，
，，
，，
；
（2），如图
，
故答案为：；
（3）如图2，，
理由是：延折叠和重合，
，
，，
，
即．
13．（2014秋•兴化市期末）（1）如图①，将纸片沿（点、分别在和上）进行折叠，当点落在四边形的边上时，请直接写出与之间的数量关系是 ；
（2）如图②，将纸片沿（点、分别在和上）进行折叠，当点落在四边形的内部时，直接写出与、之间的数量关系是 ；
（3）如图③，将纸片沿（点、分别在和上）进行折叠，当点落在四边形的外部时，写出与、之间的数量关系，并说明理由；
（4）如图④，如果将纸片沿（点在上，点在上）进行折叠，当点落在的外部，点落在的内部时，请你直接写出、与、之间的数量关系是 ．
【解答】解：（1）如图1，．
（2）如图2，．
（3）如图3，．证明如下：由题意得：（设为，（设为；
，
，
；
，
．
（4）如图4，
14．（2021春•南通期末）如图所示，把一个三角形纸片ABC的三个顶角向内折叠之后（3个顶点不重合），图中∠1+∠2+∠3+∠4+∠5+∠6＝ 360 °．
【解答】解：由题意知，
∠1+∠2+∠3+∠4+∠5+∠6＝720°﹣（∠B'FG+∠B'GF）﹣（∠C'HI+∠C'IH）﹣（∠A'DE+∠A'ED）＝720°﹣（180°﹣∠B'）﹣（180°﹣C'）＝（180°﹣A'）＝180°+（∠B'+∠C'+∠A'）
又∵∠B＝∠B'，∠C＝∠C'，∠A＝∠A'，
∠A+∠B+∠C＝180°，
∴∠1+∠2+∠3+∠4+∠5+∠6＝360°．
故答案为：360．
15．（2020秋•电白区期末）如图，在中，，将沿着直线折叠，点落在点的位置，则的度数是
A．B．C．D．
【解答】解：由折叠的性质得：，
根据外角性质得：，，
则，
则．
故选：．
16．（2022秋•东港区校级月考）如图，三角形纸片中，，，将纸片的角折叠，使点落在内，若，则的度数是
A．B．C．D．
【解答】解：延长，交于点，连接．
，，
，
，
，
，
，
故选：．
17．（2020秋•鼓楼区校级期中）如图，中，将沿直线翻折，点落在点的位置，若，则的度数是
A．B．C．D．
【解答】解：如图，
设为，为，
由翻折可得，
，
，
，
，
，
，
故选：．
18．如图，三角形纸片中，将沿折叠，使点落在外部点处，若，则，，的等量关系为
A．B．C．D．
【解答】解：，
．
由折叠可得：，．
．
．
．
．
，
．
即：．
故选：．
19．（2021春•江都区校级期末）如图，三角形纸片中，，将纸片一角折叠，使点落在的内部，若，则 ．
【解答】解：设折痕为，连接．
，，，
，
，
，
故答案为：．
20．（2016秋•醴陵市期末）如图，将纸片沿折叠，点落在点处，已知， ．
【解答】解：，，
，
，
，
，
．
故答案为
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/10/3 0:30:21；用户：微信用户；邮箱：rFmNt0ALlhXWmlRPd3BByUm_TL4@；学号：47883804