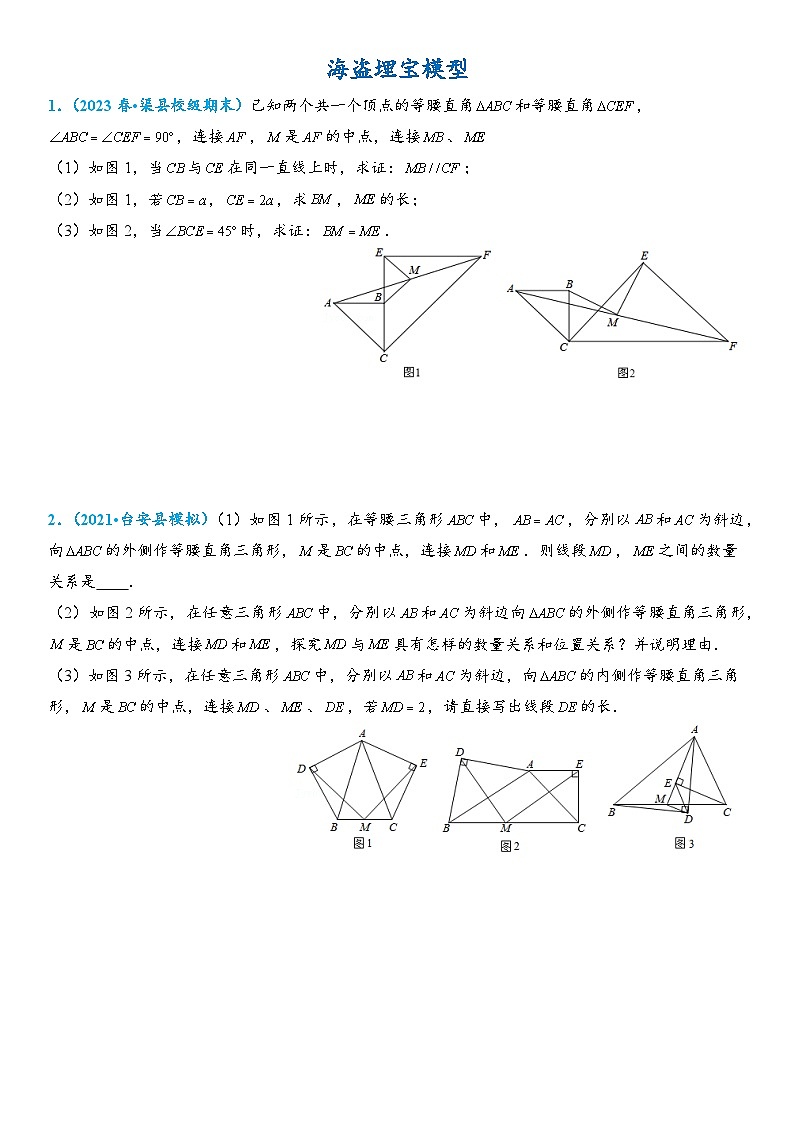
2024年中考数学压轴题专项练习—海盗埋宝模型

这是一份2024年中考数学压轴题专项练习—海盗埋宝模型，文件包含47海盗埋宝模型答案docx、47海盗埋宝模型docx等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。

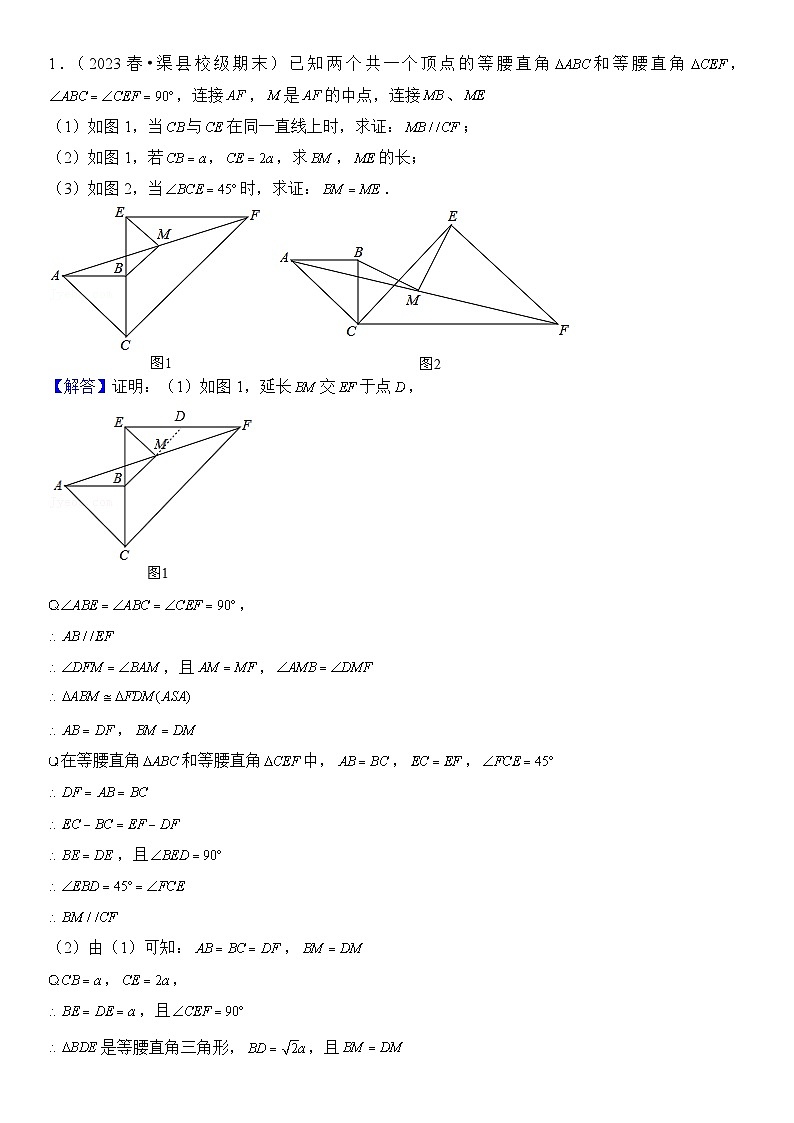
（2）如图1，若，，求，的长；
（3）如图2，当时，求证：．
【解答】证明：（1）如图1，延长交于点，
，
，且，
，
在等腰直角和等腰直角中，，，
，且
（2）由（1）可知：，
，，
，且
是等腰直角三角形，，且
，
（3）如图2，延长交于点，连接，延长与交于点，连接，
是等腰直角三角形
，，
，
，点为中点，
．
同理可得：，．
在与中，
，
，
．
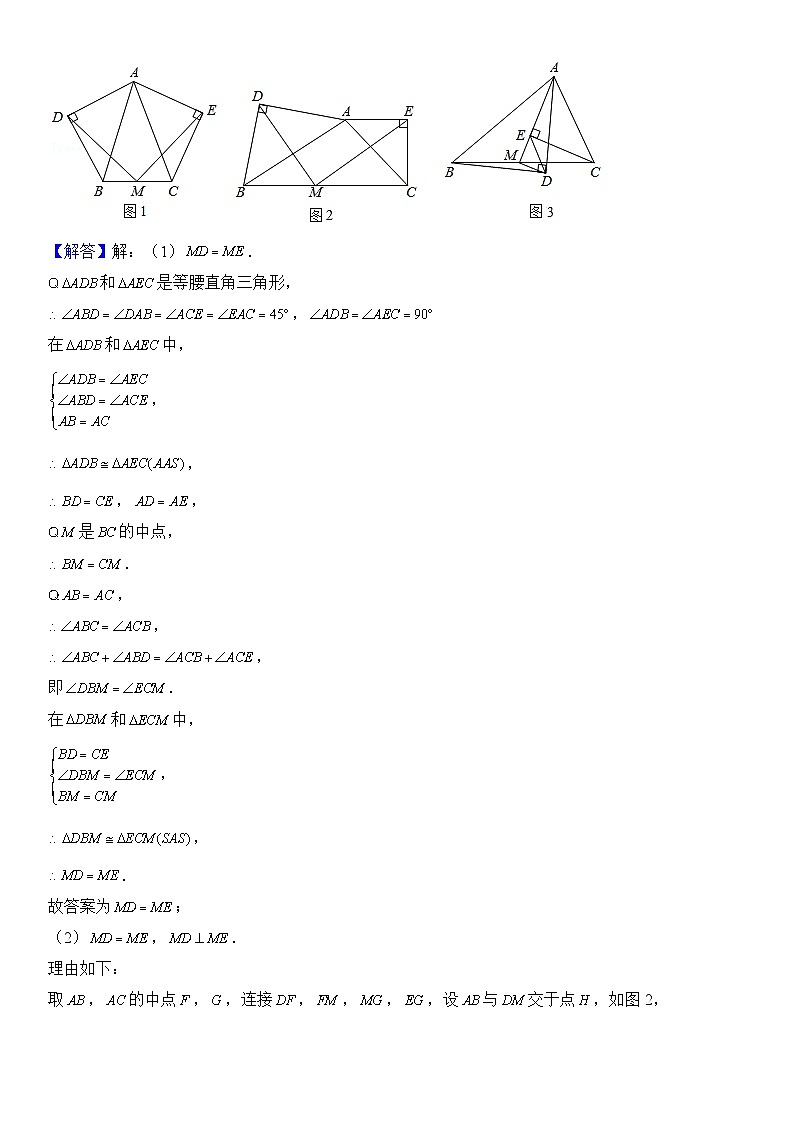
2．（2021•台安县模拟）（1）如图1所示，在等腰三角形中，，分别以和为斜边，向的外侧作等腰直角三角形，是的中点，连接和．则线段，之间的数量关系是 ．
（2）如图2所示，在任意三角形中，分别以和为斜边向的外侧作等腰直角三角形，是的中点，连接和，探究与具有怎样的数量关系和位置关系？并说明理由．
（3）如图3所示，在任意三角形中，分别以和为斜边，向的内侧作等腰直角三角形，是的中点，连接、、，若，请直接写出线段的长．
【解答】解：（1）．
和是等腰直角三角形，
，
在和中，
，
，
，，
是的中点，
．
，
，
，
即．
在和中，
，
，
．
故答案为；
（2），．
理由如下：
取，的中点，，连接，，，，设与交于点，如图2，
和都是等腰直角三角形，
，，．
点是的中点，
和都是的中位线，
，，
四边形是平行四边形，
，，
．
在和中，
，，，
，
，．
，，
，即；
（3）线段的长为，理由如下：
分别取，的中点，，连接，，，，设和交于点，如图3，
和都是等腰直角三角形，
，，．
点是的中点，
和都是的中位线，
，，
四边形是平行四边形，
，，
．
在和中，
，，，
．
，．
即．
又，
，
是等腰直角三角形，
在中，，
由勾股定理，得．
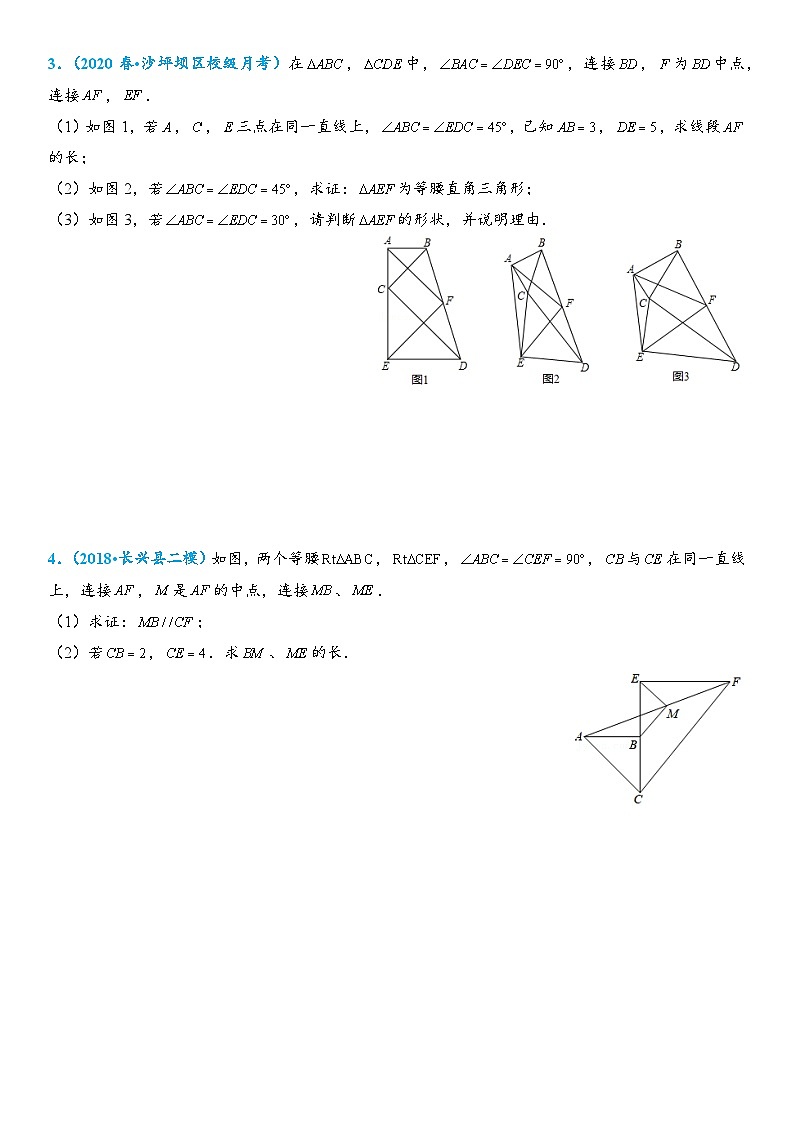
3．（2020春•沙坪坝区校级月考）在，中，，连接，为中点，连接，．
（1）如图1，若，，三点在同一直线上，，已知，，求线段的长；
（2）如图2，若，求证：为等腰直角三角形；
（3）如图3，若，请判断的形状，并说明理由．
【解答】解：（1）连接，
在，中，，
，，，
，，三点在同一直线上，
，
为的中点，
，
，
，
，
同理：，，
为等腰直角三角形，
，，
．
（2）证明：取的中点，的中点，连接，，，，
为的中点，
为的一条中位线，
，，
四边形为平行四边形，，，，
在中，为的中点，
，，
同理：，，
，，
．
，
，
，，
．
为等腰直角三角形；
（3）证明：取的中点，的中点，连接，，，，
为的中点，
为的一条中位线，
，，
四边形为平行四边形，，，，
在中，为的中点，
，，
同理：，，
，，
．
，
，
，，
．
为等边三角形．
4．（2018•长兴县二模）如图，两个等腰，，，与在同一直线上，连接，是的中点，连接、．
（1）求证：；
（2）若，．求、的长．
【解答】证明：（1）延长交于，则三角形与三角形为等腰直角三角形
为中点
又为中点
为三角形中位线
（2）延长交于
又为等腰直角三角形
为等腰直角三角形
．
5．（2023•沂源县一模）已知如图1，在中，，，点在上，交于，点是的中点
（1）写出线段与线段的关系并证明；
（2）如图2，将绕点逆时针旋转，其它条件不变，线段与线段的关系是否变化，写出你的结论并证明；
（3）将绕点逆时针旋转一周，如果，，直接写出线段的范围．
【解答】解：（1）结论：，．
理由：如图1中，
，，
，
，，
，，
，，
，
，
，．
（2）结论不变．
理由：如图2中，延长到使得，延长到，使得，连接、．、，延长交于，交于．
，，
，同法，
，
，
，
，
，
，，
，，同法，，
，
，，
，
，
，．
方法二：延长到．使得，连接，，，，证明是等腰直角三角形即可解决问题．
（3）如图3中，当点落在上时，的长最大，最大值
如图4中，当点落在的延长线上时，的值最小，最小值．
综上所述，．
6．（2021秋•荔城区校级期末）如图，四边形是正方形，点为对角线的中点．
（1）问题解决：如图①，连接，分别取，的中点，，连接，则与的数量关系是 ，位置关系是 ．
（2）问题探究：如图②，将图①中的绕点按顺时针方向旋转得到△，连接，点，分别为，的中点，连接，．试判断与之间的数量关系，并证明；
（3）拓展延伸：如图③，将图①中的绕点按逆时针方向旋转得到△，连接，点，分别为，的中点，连接，．若正方形的边长为1，求线段的长
【解答】（1）解：点为对角线的中点，
，，
为的中点，为的中点，
，，
，；
故答案为：，．
（2）结论：．
证明：如图②中，连接并延长交于点，
四边形是正方形，
，，
将绕点按顺时针方向旋转得到△，
△是等腰直角三角形，，，
，，
又点是的中点，
，
△，
，，
，
，
△为等腰直角三角形．
，，
也为等腰直角三角形．
又点为的中点，
，．
解法二：如图，取的中点，连接，
．，
，，
，，，
平分线段，
点在上，
，
，
，．
（3）解：如图③中，延长交边于点，连接，．
四边形是正方形，是对角线，
，
由旋转得，四边形是矩形，
，，
为等腰直角三角形．
点是的中点，
，，，
△，
，，
，
，
△为等腰直角三角形，
点是的中点，
，
，，
，
．
解法二：连接，取的中点，连接，．
，，
，，
．，
，，
，，
，
．
7．（2021春•沙坪坝区校级期末）如图，已知，边的中点，
（1）分别以和为腰，向的外侧作等腰三角形，其中，，且，如图1所示．
①若，求的度数；
②求证：；
（2）分别以和为斜边，向的外侧作等腰直角三角形，其中，如图2所示，连接和，则和具有怎样的数量和位置关系？请给出证明过程．
【解答】（1）①解：，，
，
．
②证明：如图1中，延长到，使得，连接，．
，，，
，
，，
，
，
，
，
，，
，，，
，
，
，
．
（2）解：如图2，取、的中点、，连接，，，，设交于．
，．
和是等腰直角三角形，
，，，，
，，．
是的中点，
，，
四边形是平行四边形，
，，．
，，，
，
，
，，
，
，
，
，
，
，
即，
，
，．
8．（2020•越秀区校级模拟）在中，，．点在边上（不与，重合），连接，为中点．
（1）若过点作于，连接、、，如图1．设，则 1 ；
（2）若将图1中的绕点旋转，使得、、三点共线，点仍为中点，如图2．求证：；
（3）若，点在边的三等分点处，将线段绕点旋转，点始终为中点，求线段长度的取值范围．
【解答】解：（1）于，为中点．
，，
．
，
；
（2）如图2，过点作的垂线交于点，设与的交点为．
由题意，，
．
、、三点共线，
．
，，
．
，，
．
．
．
．
是中点，
是中点．
在中，，
；
（3）情况1：如图，当时，取的中点，连接和，
，，且，
，．
为中点，，
，
．
为中点，为中点，
．
当且仅当、、三点共线且在线段上时最大，此时．
同理最小值为．
情况2：如图，当时，取的中点，连接和，
类似于情况1，可知的最大值为．
综合情况1与情况2，可知当点在靠近点的
三等分点时，线段的长度取得最大值为．
同理最小值为．
9．（2018•槐荫区一模）如图1，在中，，，为边上一点，且，过点作于点．
（1）求的长；
（2）如图2，将绕点顺时针旋转，延长交于点，交于点，连接．求证：点是的中点．
（3）如图3，在绕点顺时针旋转的过程中，当的延长线恰好经过点时，若点为的中点，点是的中点，连接、．求证：．
【解答】解：（1），
，
，（1分）
在中，
，即，
解得：，（2分）；
（2）由题意得：，，（3分）
则，（4分）
，
即，
，即是的中点．（5分）；
（3）点，点分别是，的中点，
，（6分）
，（7分）
由（2）可知，，
，
，（8分）
，
、、、四点共圆，（9分）
，（10分）
，
、、、四点共圆，（11分）
，
，
．（12分）
10．（2020•东明县校级二模）已知等腰和等腰中，，且
（1）发现：如图1，当点在上且点和点重合时，若点、分别是、的中点，则与的位置关系是 ，与的数量关系是
（2）探究：若把（1）小题中的绕点旋转一定角度，如图2所示，连接和，并连接、的中点、，则与的位置关系和数量关系仍然能成立吗？若成立，请以逆时针旋转得到的图形（图为例给予证明位置关系成立，以顺时针旋转得到的图形（图为例给予证明数量关系成立，若不成立，请说明理由．
【解答】解：（1），；
理由：当点在上且点和点重合时，点、分别是、的中点，
是三角形的中位线，
，
等腰和等腰中，，且，
，，
与的位置关系是：，与的数量关系是：．
故答案为：，；
（2），；
理由：如图3，连接并延长到，使，连接、、．
在和中，
，
，
，，
，
在和中，
，
，
，，
，
，
又点、分别是、的中点，
，
，
如图4，连接并延长交于，
，
，
，，
在和中，
，
，
，，
．
11．（2013•太原二模）如图（1），点是正方形的边上一点，以为边在正方形的外部作，使，，点是线段的中点，连接，，请探究线段，的数量关系和位置关系．
小颖的思路：延长交于点，通过构造全等三角形解决．
（1）请按小颖的思路解决图（1）中的问题：
①证明：；
②直接写出，的位置关系为 ，数量关系为 ．
（2）将图（1）中的绕点旋转，使落在对角线的延长线上，其余条件都不变，请写出此时，的数量关系和位置关系，并证明；
（3）将图（2）中的正方形变为菱形，其中，将等腰的顶角变为，其余条件都不变，此时线段，的位置关系为 ， ．
【解答】解：（1）①四边形是正方形，
，．
，
，
，
．．
是线段的中点，
．
在和中，
，
．
②，
．．
，
．
，
，
，
，，
．
故答案为：，；
（2），．
理由：延长交于，
四边形是正方形，
，．，
，
，
，
．
．．
是线段的中点，
．
在和中，
，
．
．．
，
．
在和中
，
，．
，
，
即，
，，
．
（3）过点作交的延长线于点，
．．
是线段的中点，
．
在和中，
，
．
．．
，
．
四边形是菱形，
．
，
是等边三角形，
．
，，
，
，，
，
．
在和中
，
，．
，
，
即，
为等边三角形，
．
，
，．
设，则，在中，由勾股定理，得
．
故答案为：，．
12．（2012•义乌市模拟）已知：是等腰直角三角形，四边形是正方形，是的中点．
（1）如图，当、、在同一直线上时，请探究和的数量关系有 ，位置关系有 ．
（2）如图，把等腰直角绕点逆时针旋转，当点恰好在射线上时：
问题①：（1）中得到的结论还成立吗？请加以证明．
问题②：若正方形的面积为1，等腰直角的面积为，的长为，求关于的函数关系式．
（3）如图，把等腰直角绕点逆时针旋转到一般位置时，请直接写出（1）中得到的结论一定 （填“成立”或“不成立” ．
【解答】解：（1）是等腰直角三角形，
，
是的中点，
，
，
四边形是正方形，
，
同理证得：，，
，
，
，
故答案为：，．
（2）①成立；
如图，在上截取，连接、，
，，
，
在和中，
，
，
，，
，
，
，，
，
在和中，
，
，
，，
，
，
，
，
四边形是正方形，
，，
（3）成立；
如图，将绕点逆时针旋转，使和重合，到位置，连接，
则，，，
，
，
，
，
在和中，
，
，
，，
，
四边形是正方形，
，．
13．（2013•南昌）某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
（1）操作发现：在等腰中，，分别以和为斜边，向的外侧作等腰直角三角形，如图1所示，其中于点，于点，是的中点，连接和，则下列结论正确的是 ①②③④ （填序号即可）
①；②；③整个图形是轴对称图形；④．
（2）数学思考：在任意中，分别以和为斜边，向的外侧作等腰直角三角形，如图2所示，是的中点，连接和，则和具有怎样的数量关系？请给出证明过程；
（3）类比探究：
在任意中，仍分别以和为斜边，向的内侧作等腰直角三角形，如图3所示，是的中点，连接和，试判断的形状．答： ．
在三边互不相等的中（见备用图），仍分别以和为斜边，向的内侧作（非等腰）直角三角形和（非等腰）直角三角形，是的中点，连接和，要使（2）中的结论此时仍然成立，你认为需增加一个什么样的条件？（限用题中字母表示）并说明理由．
【解答】解：（1）和是等腰直角三角形，
，
在和中，
，
，
，，
于点，于点，
，．
，
，故①正确；
是的中点，
．
，
，
，
即．
在和中
，
．故②正确；
连接，根据前面的证明可以得出将图形1，沿对折左右两部分能完全重合，
整个图形是轴对称图形，故③正确．
，，
，
，
，
四边形四点共圆，
．
是对称轴，
，
，
，故④正确，
故答案为：①②③④．
（2），
理由：取、的中点、，连接，，，，
，．
和是等腰直角三角形，
，，，，
，，．
是的中点，
，，
四边形是平行四边形，
，，．
，，，
．
在和中，
，
，
；
（3）点、、分别是、、的中点，
，，，，
四边形是平行四边形，
，．．
和是等腰直角三角形，
，，
，，，
即．
在和中
，
，
，．
，
，
，
，
即，
为等腰直角三角形；
如图4，和是直角三角形，，当时，．
理由：取、的中点、，连接，，，，
，，，，
四边形是平行四边形，
，，．
，
，，
，，，．
，
，
，
，
即．
在和中，
，
，
．
14．如图，在等腰中，，，为射线上一点不与重合）．
（1）当时，求证：是直角三角形．
（2）当是以为腰的等腰三角形时，求的面积．
（3）作点关于的对称点，当直线与中或所在直线垂直时，求的长．
【解答】（1）证明：，
，
在中，
，
，
，
，
，
是直角三角形．
（2）解：是以为腰的等腰三角形，
或，
不与重合，
，
，
，
过点作于点，如图，
由（1）知，，，，
则，
．
（3）解：作点关于的对称点，连接交于，交于，如图，
若，
根据对称的性质可知，，，
在和中，
，
，
，
设的长为，则，
易知，
，
根据可得方程，
解得：；
若，
，，
易知，
此时点在点的左侧，不在射线上，此情况不符合题意．
综上，的长为．