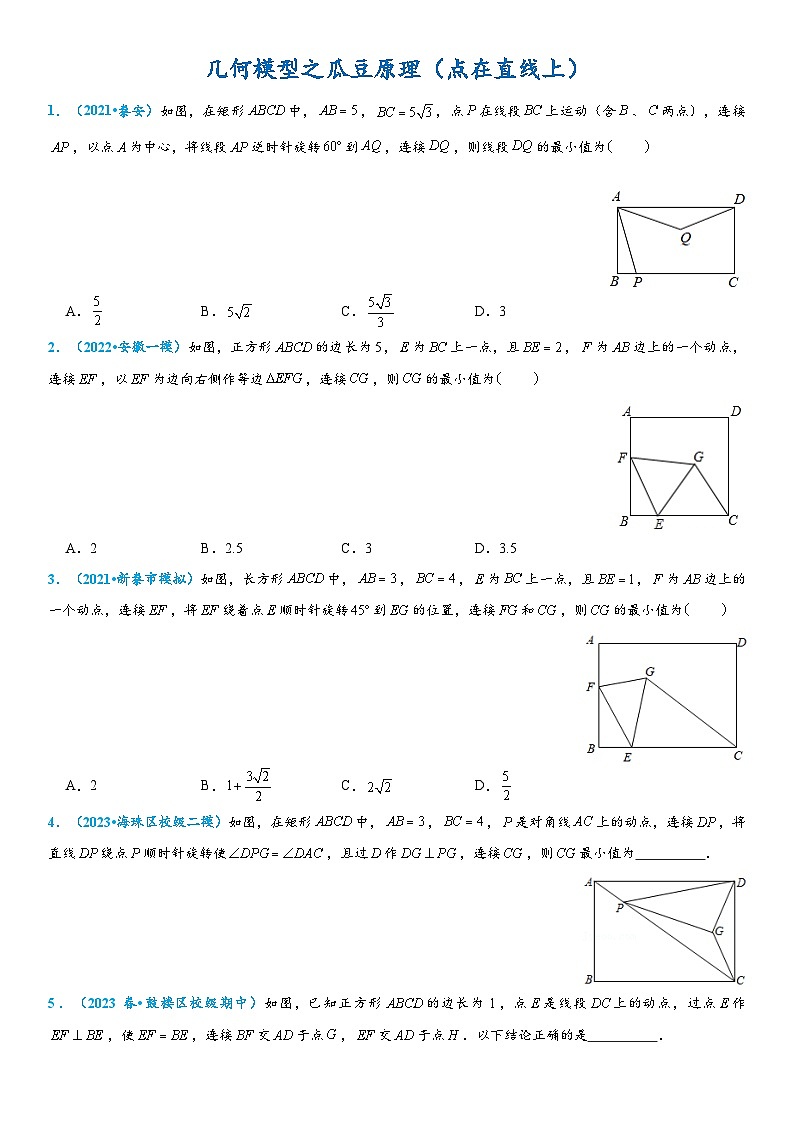
2024年中考数学压轴题专项练习—几何模型之瓜豆原理（点在直线上）

这是一份2024年中考数学压轴题专项练习—几何模型之瓜豆原理（点在直线上），文件包含94几何模型之瓜豆原理点在直线上答案docx、94几何模型之瓜豆原理点在直线上docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。

A．B．C．D．3
【解答】解：如图，以为边向右作等边，作射线交于点，过点作于．
四边形是矩形，
，
，都是等边三角形，
，，，
，
在和中，
，
，
，
，
，
，，
点在射线上运动，
，
，
，，
，
根据垂线段最短可知，当点与重合时，的值最小，最小值为，
故选：．
2．（2022•安徽一模）如图，正方形的边长为5，为上一点，且，为边上的一个动点，连接，以为边向右侧作等边，连接，则的最小值为
A．2B．2.5C．3D．3.5
【解答】解：由题意可知，点是主动点，点是从动点，点在线段上运动，点也一定在直线轨迹上运动，
将绕点旋转，使与重合，得到，
，，，
为等边三角形，点在垂直于的直线上，
作，则即为的最小值，
作，可知四边形为矩形，
，
，
则，
故选：．
3．（2021•新泰市模拟）如图，长方形中，，，为上一点，且，为边上的一个动点，连接，将绕着点顺时针旋转到的位置，连接和，则的最小值为
A．2B．C．D．
【解答】解：如图，将线段绕点顺时针旋转得到线段，连接，连接交于．
四边形是矩形，
，，
，
，
在和中，
，
，
，
点的在射线上运动，
当时，的值最小，
，，，
，
，
，
四边形是矩形，
，，
，
，
，
，
的最小值为，
故选：．
二．填空题（共13小题）
4．（2023•海珠区校级二模）如图，在矩形中，，，是对角线上的动点，连接，将直线绕点顺时针旋转使，且过作，连接，则最小值为 ．
【解答】解：如图，作于，连接延长交于，作于．
，，
，
，
，
，，
，
，
定值，
点在射线上运动，
当时，的值最小，
四边形是矩形，
，
，
，
，
，
，，
，
，
在中，，，，
，，
，
，
，，，
，
，
的最小值为，
故答案为．
5．（2023春•鼓楼区校级期中）如图，已知正方形的边长为1，点是线段上的动点，过点作，使，连接交于点，交于点．以下结论正确的是 ①④ ．
①；
②；
③点到直线的距离最大值为；
④点到直线的距离最大值为．
【解答】解：①正方形中，．
，
．
如图：，；
．
．故①正确．
②当点向左移动时，逐渐减小，而增大；故②错误．
③延长至，使，连接．
，
，．
，，
．
，
，
．
．
．
．
过作的延长线于．
．
．
点是线段上的动点，，故③错误．
④过作于．
，
，
．
，
；即：，
设，则：，
当时，取得最大值：．故④正确；
故答案为：①④．
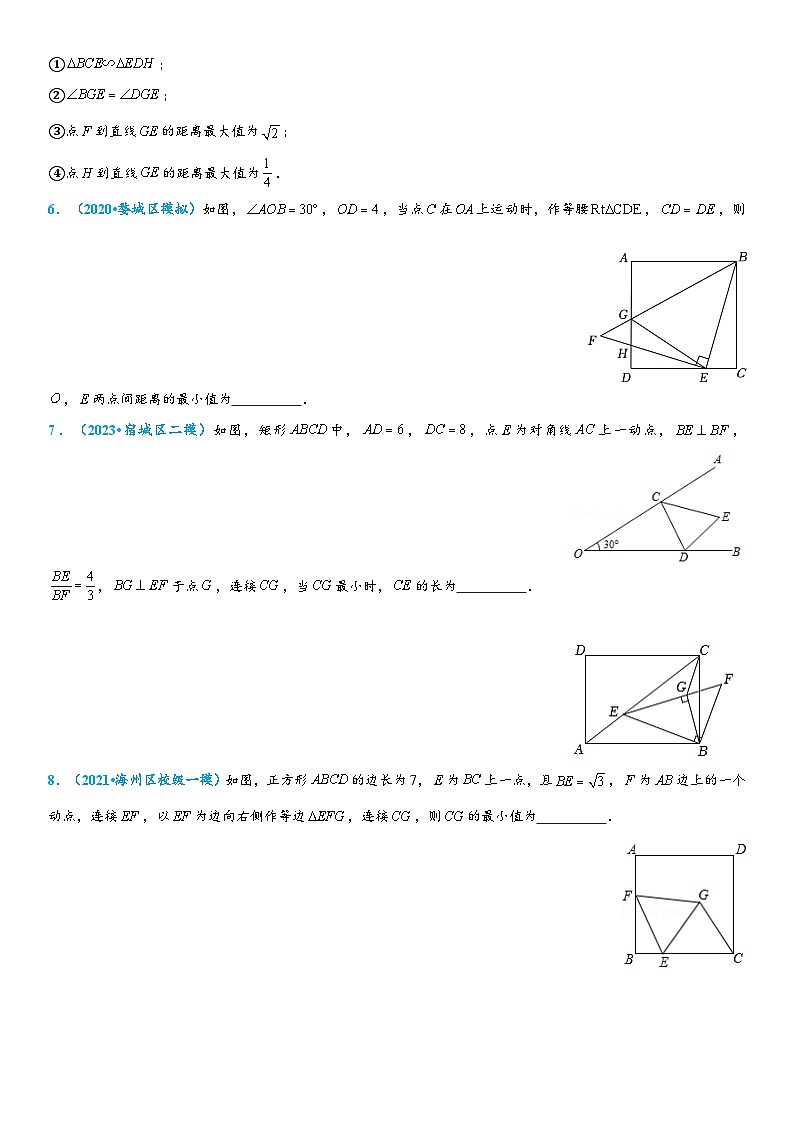
6．（2020•婺城区模拟）如图，，，当点在上运动时，作等腰，，则，两点间距离的最小值为 ．
【解答】解：，，点在上运动时，，，
为主动点，为从动点，为定点，
由“瓜豆原理”， 在上运动，则在垂直的直线上运动，
当时，如答图：
过作于，交于，则直线即为的运动轨迹，的长为，两点间距离的最小值，
，，，
，
，
，
，
，
而，
，，
在中可得，
，
中可得，
故答案为：．
7．（2023•宿城区二模）如图，矩形中，，，点为对角线上一动点，，，于点，连接，当最小时，的长为 ．
【解答】解：如图，过点作于点，连接，
，，
，
，
，
，
，，
，
，
，
即在点的运动过程中，的大小不变且等于，
当时，最小，
设此时，
，
，
，
，
，
代入，解得，
，
，
，
故答案为：．
8．（2021•海州区校级一模）如图，正方形的边长为7，为上一点，且，为边上的一个动点，连接，以为边向右侧作等边，连接，则的最小值为 ．
【解答】解：为等边三角形，
，
把绕点顺时针旋转得到，如图，延长交于，过点作，过点作，
，，，
即点在过点且垂直于的线段上，
易得四边形为矩形，
，，
，
，
．
的最小值为．
故答案为．
9．（2021秋•东台市期中）如图，在矩形中，对角线，相交于点，，，点在线段上从点至点运动，连接，以为边作等边三角形，点和点分别位于两侧，则点运动的路程长是 ．
【解答】解：连接，
四边形是矩形，
，，
，
是等边三角形，
，，
是等边三角形，
，，
，
又，，
，
，，
点在射线上运动，且，
当点在线段上从点至点运动时，
点的运动路程是，
在中，设，则，
，
解得（负值舍去），
，
即点的运动路程为，
故答案为：．
10．（2020•东台市一模）如图，已知点，，，动点在线段上，点、、按逆时针顺序排列，且，，当点从点运动到点时，则点运动的路径长为 6 ．
【解答】解：点，，
，
，动点在线段上，，，
，为主动点，为从动点，为定点，
由“瓜豆原理”得运动路径与运动路径之比等于，
点运动的路径长为，
故答案为：6．
11．（2021•秦都区模拟）如图，正方形的边长为2，为上一点，且，为边上的一个动点，连接，以为底向右侧作等腰直角，连接，则的最小值为 ．
【解答】解：如图1，过点作于点，于点，连接，
根据题意知，，．
．
．
又是等腰直角三角形，且，
．
在与中，
，
．
，．
点在所在的直线上运动．
为边上的一个动点，如图2，
当点与点重合时，点的位置如图所示．
当点与点重合时，记点的位置为．
点的运动轨迹为线段．
过点作于点．
．
正方形的边长为2，
．
．
故答案为：．
12．（2020秋•鼓楼区校级月考）如图，正方形的边长为4，为上一点，且，为边上的一个动点，连接，将绕点顺时针旋转得到，连接，则的最小值为 ．
【解答】解：将线段绕顺时针旋转至，连接，过作于，过作于，如图：
，
，
在和中，
，
，
，
在射线上运动，
，
的长度即是的最小值，
，，，
四边形为矩形，
，
中，，，
，
，
故答案为：．
13．（2021秋•鼓楼区校级期末）如图，在中，，，，点在边上运动（可与点，重合），将线段绕点逆时针旋转，得到线段，连接，，则长的最小值为 ．
【解答】解：如图所示，以为底边向上作等腰，使，连接．
由题意可得和均为顶角为 的等腰三角形，
可得，，
，
，
，
，
当时，有最小，即此时最小，
如图所示，设，延长与交，此时为的最小值，
可得，
中，，，
，，
，
，，
，
，，
，，
，
，
，
，
．
14．（2020•邗江区校级一模）如图，菱形的边长为4，，是的中点，是对角线上的动点，连接，将线段绕点按逆时针旋转，为点对应点，连接，则的最小值为 ．
【解答】解：如图取的中点，连接，，，延长交于，作于．
四边形是菱形，
，，，
，
，
，
，，
，
是等边三角形，
，，，
，
，
，
，
，
，
，
点在直线上运动，
根据垂线段最短可知，当点与重合时，的值最小，
在中，，，，
，
的最小值为，
故答案为．
15．（2021秋•忠县期末）如图，在中，，点在边上，，，点是边所在直线上的一动点，连接，将绕点顺时针方向旋转得到，连接，则的最小值为 ．
【解答】解：如图，以为边作等边三角形，连接，过点作于，
，，
，
是等边三角形，，
，，，
，
将绕点顺时针方向旋转得到，
，，
，
，
在和中，
，
，
，
当有最小值时，有最小值，
由垂线段最短可得：当时，有最小值，
此时，，，，
四边形是矩形，
，
故答案为：．
16．（2019秋•两江新区期末）已知边长为6的等边中，是高所在直线上的一个动点，连接，将线段绕点逆时针旋转得到，连接，则在点运动的过程中，当线段长度的最小值时，的长度为 ．
【解答】解：连接，
等边，
，
线段绕点逆时针旋转得到，
，，
，
点在直线上运动，
，，
点在直线上运动，
当时，最小，
，
，
，
，
，
故答案为．
三．解答题（共4小题）
17．（2021秋•武昌区期末）如图1，在中，平分，平分，与交于点．
（1）若，则 ；
（2）如图2，，作交于点，求证：；
（3）如图3，，，若点为的中点，点在直线上，
连接，将线段绕点逆时针旋转得，，连接，当最短时，直接写出的度数．
【解答】（1）解：，
，
平分，平分，
，，
，
，
故答案为：；
（2）证明：如图2，过点作于，于，于，
平分，平分，于，于，于，
，
，
，
，
，
，
又，
，
；
（3）如图3，过点作，且，连接，
，，
，
，
将线段绕点逆时针旋转得，
，，
，
又，，
，
，
点在直线上运动，
当时，有最小值为，
此时，延长交于，连接，设与的交点为，
，，
，，
，，
点是的中点，
，
又，
△，
，
，
，
点与点重合，
，，
，
，
，
，
当最短时，的度数度数为．
18．（2022•沈阳）【特例感知】
（1）如图1，和是等腰直角三角形，，点在上，点在的延长线上，连接，，线段与的数量关系是 ；
【类比迁移】
（2）如图2，将图1中的绕着点顺时针旋转，那么第（1）问的结论是否仍然成立？如果成立，证明你的结论；如果不成立，说明理由．
【方法运用】
（3）如图3，若，点是线段外一动点，，连接．
①若将绕点逆时针旋转得到，连接，则的最大值是 ；
②若以为斜边作，，三点按顺时针排列），，连接，当时，直接写出的值．
【解答】解：（1）．理由如下：
如图1，和是等腰直角三角形，，
，，
在和中，
，
，
，
故答案为：；
（2）仍然成立
证明：如图2，，
，
即，
在和中，
，
，
；
（3）①过点作，使，连接，，，，
和都是等腰直角三角形，
，，，
，，
，
，
，
，，
点的运动轨迹是以为圆心，为半径的圆，
当在的延长线上时，的值最大，最大值为，
故答案为：；
②如图4，在上方作，过点作于点，连接、、，过点作于点，
，，
，
，
，
在中，，
，
，
，
，，
在中，，
；
如图5，在上方作，过点作于点，连接，
则，
，
，
，
，
，，
，
；
综上所述，的值为或．
19．（2021•新市区校级一模）如图①，二次函数的图象与轴交于点、，与轴交于点，连接，点是抛物线上一动点．
（1）求二次函数的表达式．
（2）当点不与点、重合时，作直线，交直线于点，若的面积是面积的4倍，求点的横坐标．
（3）如图②，当点在第一象限时，连接，交线段于点，以为斜边向外作等腰直角三角形，连接，的面积是否变化？如果不变，请求出的面积；如果变化，请说明理由．
【解答】解：（1）二次函数经过，，
代入得，
解得，
所以二次函数的表达式为．
（2）①如图所示，当在轴上方时，
过点作轴于点，过点作轴于点，过点作于点，
可得，
，
，
，
，
设点，
，，
，，
，
，
点的坐标可表示为，，
，为二次函数与轴交点，
，
可得的解析式为，
在上，
，
解得或．
②如图所示，当在轴下方时，
同理①可求出点的横坐标为或，
，
当点横坐标为时，在抛物线的段，
综上所述，点的横坐标为或或或．
（3）如图所示，以为底在轴上方作等腰直角三角形，连接，过点作轴于点，
和均为等腰直角三角形，
，，
，
，
，
，
，，
，
，
，
两条平行线之间的距离相等，
在运动时，到的距离保持不变，其距离都等于的长，
在等腰直角三角形中，，
，
．
综上所述，的面积不变，为4．
20．如图，在等边中，，，垂足为，点为边上中点，点为直线上一点．当点为中点，点在边上，且，点从中点沿射线运动，将线段绕点顺时针旋转得到线段，连接，当最小时，直接写出 的面积．
【解答】解：以为顶点，为一边，作，交于点，过点作于点，设交于点，如图，
中，，
最小即最小，此时、、共线，
将线段绕点顺时针旋转得到线段，
在射线上运动，则点在上运动，根据“瓜豆原理”， 为主动点，是从动点，为定点，，则、轨迹的夹角，
，
，
，
，
，
，
，
，
，
，
四边形为矩形，
，
等边中，，，
，
又，
等边中，，点为的中点，点为中点，
，，
中，，，
，，
中，，
，
．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/9/10 23:26:15；用户：微信用户；邮箱：rFmNt0ALlhXWmlRPd3BByUm_TL4@；学号：47883804