2024年中考数学压轴题专项练习—角平分线模型

这是一份2024年中考数学压轴题专项练习—角平分线模型，文件包含40角平分线模型答案docx、40角平分线模型docx等2份试卷配套教学资源，其中试卷共78页， 欢迎下载使用。
（1）求证：；
（2）作，垂足为点，．
①设，请用含的代数式表示梯形的面积；
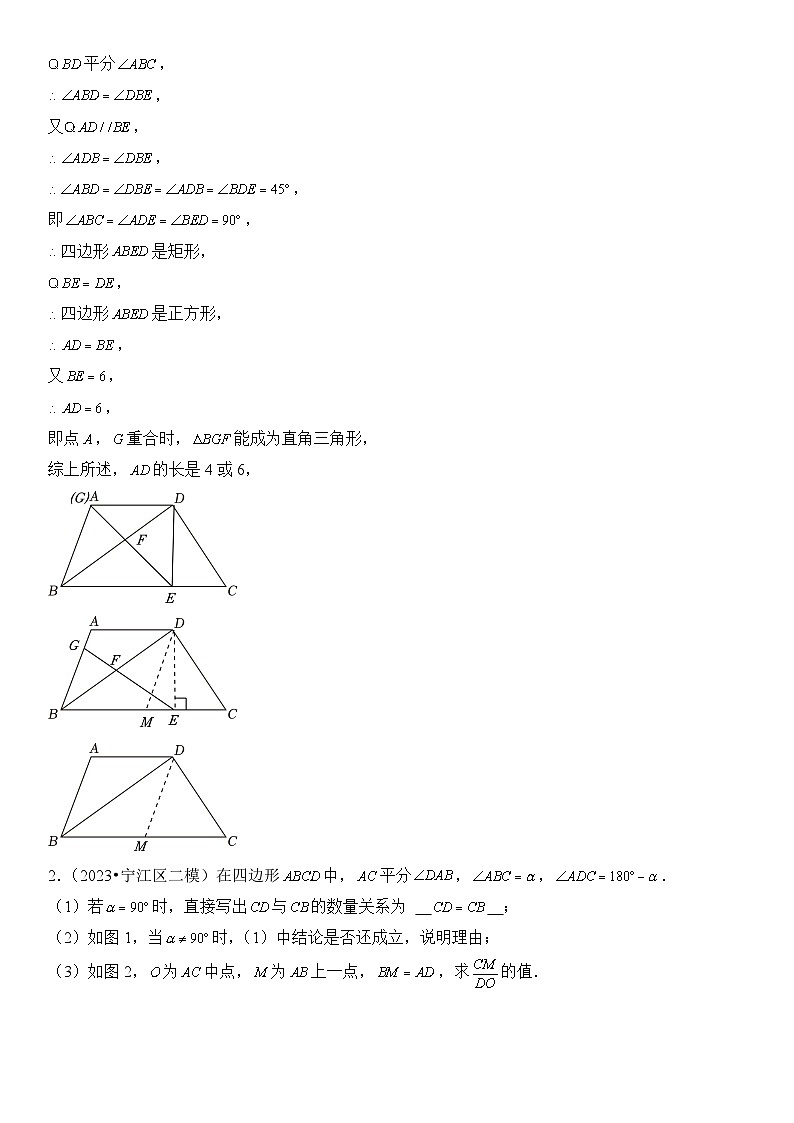
②点为中点，联结并延长，交边于点，请你想一想， 能否成为直角三角形，如果能，请求出此时线段的长，如果不能，请说明理由．
2．（2023•宁江区二模）在四边形中，平分，，．
（1）若时，直接写出与的数量关系为 ；
（2）如图1，当时，（1）中结论是否还成立，说明理由；
（3）如图2，为中点，为上一点，，求的值．
3．（2023春•二道区校级期中）【问题】
如图①，在中，，平分，平分．求的度数，对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）．
解：（三角形内角和．
（等式性质）．
（已知），
（等量代换）．
平分（已知），
（角平分线的定义）．
同理， ；
（等式性质）．
，
（等式性质）．
【拓展】如图②，在中，，平分，平分．
则 ．
【应用】如图③，在中，平分，平分，平分，平分．若，则 ．
4．（2023春•渝中区校级期中）在中，为边上一点，连接，为上一点，连接，
（1）如图1，延长交于点，若平分，平分，，，，求的周长；
（2）如图2，连接，若，，为中点，连接，请猜想线段，，之间的数量关系，并证明你的猜想；
（3）如图3，在第（2）问的条件下，当时，点是直线上一动点，连接，将沿着翻折得，连接，为的中点，连接，当点到的距离最小时，直接写出的值．
5．（2022秋•南关区校级月考）【感知】如图①所示，在等腰中，，平分，易得（不需要证明）．
【探究】如图②所示，李丽同学将图①的等腰改为任意，平分，他通过观察、测量，猜想仍然成立，为了证明自己的猜想，他与同学进行交流讨论，得到了证明猜想的两种方法：
方法1：过点分别作：于点，于点，利用与的面积比证明结论．
方法2：过点作交延长线于点，利用与相似证明结论．
请你参考上面的两种方法，选择其中的一种方法完成证明．
【应用】如图③所示，在中，，，，平分．若点在边上，，交于点，则 ．
6．（2022春•丹阳市期末）【阅读材料】
像，，，，两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式．
例如，与，与，与，，等都是互为有理化因式．进行二次根式计算时，利用有理化因式，可以化去分母中的根号．
【解决问题】
（1）的有理化因式为 ；
（2）化简：；
（3）①如图1，中，，，，点到边的距离为 ；
②如图2，中，与的角平分线相交于点，若的周长为，面积为3，则点到边的距离为 ．
7．（2022春•萍乡期中）已知是的平分线，点是射线上一点，，点、分别在射线、上，连接、．
（1）如图①，当，时，则与的数量关系是 ；
（2）如图②，点、在射线、上滑动，且，当时与在（1）中的数量关系还成立吗？说明理由．
（3）在问题（2）中，则四边形的面积是否会发生变化？若不会发生变化，请直接写出面积的值，若发生变化，请说明理由．
8．（2021秋•北安市校级期末）如图1，在平面直角坐标系中，直线与轴交于点，与轴交于点，且，满足：．
（1）求：①，的值；②的值；
（2）为延长线上一动点，以为直角边作等腰直角，连接，求直线与轴交点的坐标；
（3）如图2，点为轴正半轴上一点，且，平分，点是射线上一动点，点是线段上一动点，直接写出的最小值；（图1与图2中点的坐标相同）
（4）在（3）的条件下，当最小时，射线交于，点坐标为，当三角形为等边三角形时，直接写出点坐标．
9．（2021秋•天山区校级期中）如图所示：中，是高，、是角平分线，它们相交于点，，，求，的度数是多少？
10．（2021春•东海县期中）在数学学习过程中，对有些具有特殊结构，且结论又具有一般性的数学问题我们常将其作为一个数学模型加以识记，以积累和丰富自己的问题解决经验
【结论发现】小明在处理教材第43页第21题后发现：三角形的一个内角平分线与另一内角的外角平分线的夹角的度数是三角形第三内角度数的一半．
【结论探究】（1）如图1，在中，点是内角平分线与外角的平分线的交点，则有，请补齐下方的说理过程．
理由如下：因为，
又因为在中，，
所以．
所以 （理由是：等式性质）
同理可得 ．
又因为和分别是和的角平分线，
所以， ．
所以
即
所以．
请直接应用上面的“结论发现”解决下列问题：
【简单应用】（2）如图2，在中，．延长至，延长至，已知、的角平分线与的角平分线及其反向延长线交于、，求的度数；
【变式拓展】（3）如图3，四边形的内角与外角的平分线形成如图所示形状．
①已知，，求的度数；
②直接写出与的关系．
11．（2021秋•沂水县期中）【问题提出】在中，，为的角平分线，探究线段，，的数量关系．
【问题解决】如图1，当，过点作，垂足为，易得；由此，如图2，当时，猜想线段，，有怎样的数量关系？给出证明．
【方法迁移】如图3，当，为的外角平分线时，探究线段，，又有怎样的数量关系？直接写出结论，不证明．
12．（2023•黄石）如图，为的直径，和相交于点，平分，点在上，且，交于点．
（1）求证：是的切线；
（2）求证：；
（3）已知，求的值．
13．（2023春•城关区校级期中）小明在学习过程中，对一个问题做如下探究．
【习题回顾】如图1，在中，，是角平分线，是高，，相交于点．求证：；
【变式思考】如图2，在中，，是边上的高，若的外角的平分线交的延长线于点，其反向延长线与边的延长线交于点，判断与还相等吗？并说明理由；
【探究延伸】如图3，在中，在上存在一点，使得，角平分线交于点，交于点．的外角的平分线所在直线与的延长线交于点，请直接写出与之间的数量关系．
14．（2022秋•古冶区期中）如图：在∠EAF的平分线上取点B作BC⊥AF于点C，在直线AC上取一动点P．在直线AE上取点Q使得BQ＝BP．
（1）如图1，当点P在点线段AC上时，∠BQA+∠BPA＝ °；
（2）如图2，当点P在CA延长线上时，探究AQ、AP、AC三条线段之间的数量关系，说明理由；
（3）在满足（1）的结论条件下，当点P运动到在射线AC上时，直接写出AQ、AP、PC三条线段之间的数量关系为： ．
15．（2023春•新宾县期末）已知AG平分∠BAD，∠BAG＝∠BGA，点E、F分别在射线AD、BC上运动，满足∠AEF＝∠B，连接EG．
（1）如图1，当点F在点G左侧时，求证：AB∥EF；
（2）如图2，当点F在点G右侧时，设∠BAG＝α，∠GEF＝β，请直接用含α，β的代数式表示∠AGE的度数 ；
（3）在射线BC下方有一点H，连接AH、EH，满足∠BAH＝2∠HAG，EH平分∠FEG，若∠FEG＝20°，∠BAG＝60°，请直接写出∠AGE+∠H的度数 ．
16．（2023•荔城区校级开学）如图1，像我们常见的学习用品——圆规，我们把这样图形叫做“规形图”．
（1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；
（2）请你直接利用以上结论，解决以下三个问题：
①如图2，把一块直角三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，∠A＝54°，则∠ABX+∠ACX＝ °；
②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE＝α，∠DBE＝β，请用含α和β的式子表示∠DCE的度数．
17．（2023春•商水县期末）【基本模型】
（1）如图1，在中，平分，平分外角，试说明．
【变式应用】
（2）如图2，，，分别是射线，上的两个动点，与的平分线的交点为，则点，的运动的过程中，的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由．
【拓展应用】
（3）如图3，，作的平分线，是射线上的一定点，是直线上的任意一点（不与点重合），连接，设的平分线与的邻补角的平分线的交点为，请直接写出的度数．
18．（2023春•高港区期中）如图，已知，，两点分别是、上的两动点，，分别平分和，射线的反向延长线与射线相交于点．
（1）如图1，若，求的度数；
（2）如图2，作的角平分线交射线于点，求的度数；
（3）如图3，、为线段和上的两定点，若将沿翻折，点对应点在的内部，且满足，，请求出与，的关系．
19．（2023春•翠屏区期末）如图，已知在中，，，垂足为点，是外角的平分线，，垂足为点，，．
（1）求证：四边形为矩形；
（2）当满足什么条件时，四边形是一个正方形？并证明；
（3）在矩形中内部有一动点，满足，求的最小值．
20．（2023春•连山区月考）如图，在中，，，，点从点出发，以每秒1个单位长度的速度沿折线运动，设点的运动时间为秒．
（1）求斜边的长；
（2）当点在的角平分线上，求的值；
（3）在整个运动过程中，直接写出是等腰三角形时的值．
21．（2023•晋中模拟）阅读下列材料并完成任务．​
任务：
（1）上述证明过程中的“依据”是指什么？
（2）请按照上面的证明思路，写出该证明过程的剩余部分；
（3）如图3，在△ABC中，∠BAC＝90°，点I是△ABC的一个旁心且在BC边的下方．
①利用尺规作出旁心I；（保留作图痕迹，不写作法）
②若∠ACB＝30°，△ABC外接圆的半径为2，则AI＝ ．
22．（2023春•金华期末）佛堂古镇的万善浮桥，其夜晚的灯光秀美轮美奂，两岸景观照明还荣获了中国照明学会第十六届照明奖的一等奖．如图所示，记浮桥两岸所在直线分别为、，且，浮桥上装有两种不同的激光灯和激光灯（假设、以及由、两点发出的光射线始终在同一平面内）．灯的光射线以2度每秒的速度从射线顺时针旋转至射线后继续回转，灯的光射线以5度每秒的速度从射线顺时针旋转到射线后也继续回转．当打开激光灯的总开关时，激光灯和激光灯同时开始转动．
（1）若购买2盏灯和4盏灯共需10万元，购买3盏灯和2盏灯共需8.6万元，请问：购买灯和灯的单价分别是多少万元？
（2）打开总开关，当灯的光射线第一次从射线旋转至射线的过程中，求灯和灯的光射线恰好互相垂直时所需要的时间．
（3）如图，打开总开关，当灯的光射线第一次从射线旋转至射线的过程中，若灯和灯的光射线有交点（记为点，延长至点，作与的角平分线并交于点，求与的数量关系．
23．（2023•诸暨市模拟）在中，平分交于点，点是射线上的动点（不与点重合），过点作交直线于点，的角平分线所在的直线与射线交于点．
（1）如图1，点在线段上运动．
①若，，则 ；
②若，求的度数；
（2）若点在射线上运动时，探究与之间的数量关系．
24．（2023•驿城区三模）我国的纸伞工艺十分巧妙．如图①，伞不论张开还是缩拢，伞柄AP始终平分同一平面内两条伞骨所成的角∠BAD，从而保证伞圈C能沿着伞柄滑动．小明受此启发设计了一个“简易平分角仪器”，如图②，其中AB＝AD，BC＝DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们落在角的两边上，沿AC画一条射线AE，则AE为∠PRQ的平分线．
（1）如图②，试说明这个平分角的仪器的制作原理；
（2）如图③，将上述平分角仪器的顶点A落在⊙O的直径MN的端点M处，边AB与直径MN共线，边AD与⊙O相交于点G，AC交⊙O于点E，过点E作⊙O的切线，与AD，BC分别交于点F，H．
①求证：EF⊥AD；
②若⊙O半径为3，AE＝4，求EF的长．
25．（2023春•海安市期末）如图，在中，．过点作．
（1）判断是否平分，并说明理由；
（2）如图2，点是射线上一动点（不与点，重合），平分交射线于，过点作于．
①当点在点左侧时，若，求的度数；
②点在运动过程中，和之间有怎样的数量关系？请写出你的猜想，并说明理由．
26．（2023春•道里区校级期中）如图1，是中边上的高，点是上一点，连接交于点，．
（1）求证：；
（2）若，求证：；
（3）如图2，在（2）的条件下，延长至点，连接，，若，求线段的长．（注不能应用等腰三角形的相关性质和判定）
27．（2022•西乡塘区校级开学）【习题回顾】如图1，在中，角平分线、交于点．求的度数．
（1）若，请直接写出 ．
【变式思考】
（2）试猜想与的数量关系，并说明理由；
【拓展延伸】
（3）如图2，在中，角平分线、交于点，，交边于点，点在的延长线上，作的平分线交的延长线于点．若，求和的度数．
28．（2022秋•庐阳区校级月考）如图，中，，是的外角，和的平分线交于点，过作交的延长线于点，交延长线于点．
（1）求度数；
（2）求证：；
（3）若，，求的长．
29．（2022秋•东昌府区校级期末）如图1，中，，、的平分线交于点，过点作交、于、．
（1）猜想：与、之间有怎样的关系．
（2）如图2，若，其他条件不变，在第（1）问中与、间的关系还存在吗？并说明理由．
（3）如图3，若中的平分线与三角形外角平分线交于，过点作交于，交于．这时图中还有等腰三角形吗？与、关系又如何？说明你的理由．
30．（2022秋•即墨区期末）三角形内角和定理告诉我们：三角形三个内角的和等于如何证明这个定理呢？我们知道，平角是，要证明这个定理就是把三角形的三个内角转移到一个平角中去，请根据如下条件，证明定理．
【定理证明】
已知：如图①，求证：．
【定理推论】如图②，在中，有，点是延长线上一点，由平角的定义可得，所以 ，从而得到三角形内角和定理的推论：三角形的外角等于与它不相邻的两个内角的和．
【初步运用】如图③，点、分别是的边、延长线上一点．
（1）若，，则 ．
（2）若，则 ．
【拓展延伸】如图④，点、分别是四边形的边、延长线上一点．
（1）若，，则 ．
（2）分别作和的平分线、，如图⑤，若，则和的关系为 ．
（3）分别作和的平分线，交于点，如图⑥，求出，和的数量关系，并说明理由．
三角形的旁心
三角形一个内角的平分线和其他两个内角的外角平分线的交点，称为三角形的旁心，每个三角形有三个旁心．如图1，∠BAC的平分线与△ABC另外两个内角∠ABC，∠ACB的外角平分线相交于点O，则点O是△ABC的一个旁心．
旁心与三角形的半周长（即周长的一半）关系密切，如图2，过△ABC的旁心O分别作OD⊥BC于点D，OE⊥AB交AB的延长线于点E，OF⊥AC交AC的延长线于点F，则AE＝（AB+BC+AC）．
下面是部分证明过程：
∵BO平分∠CBE，OE⊥BE，OD⊥BC，
∴OD＝OE．（依据）
同理可得OD＝OF，OE＝OF．…