



2024年中考数学压轴题专项练习—婆罗摩笈多模型
展开(2);
(3).
【解答】(1)证明:延长到点,使,连接,
是中边上的中线,
,
在和中
,
,,
,,
,
,
,
在和中
,
,
;
(2)证明:由(1)得,
,
,
,
即;
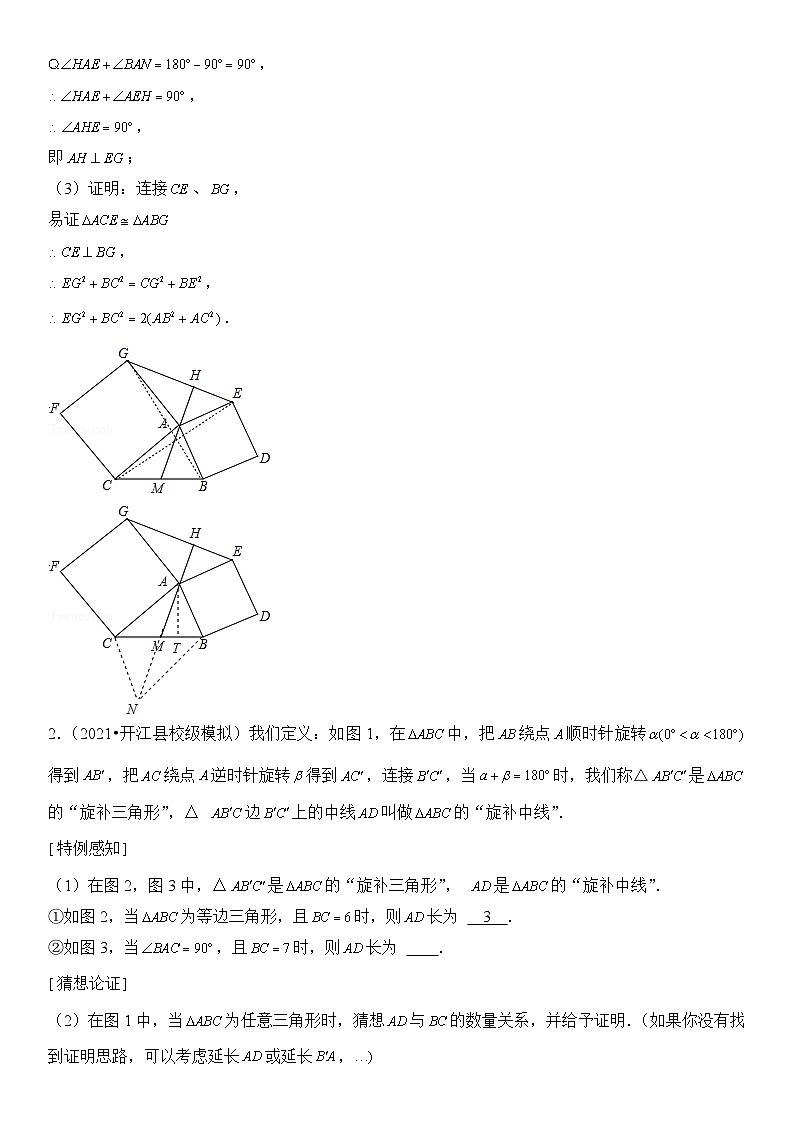
(3)证明:连接、,
易证
,
,
.
2.(2021•开江县校级模拟)我们定义:如图1,在中,把绕点顺时针旋转得到,把绕点逆时针旋转得到,连接,当时,我们称△是的“旋补三角形”,△ 边上的中线叫做的“旋补中线”.
特例感知
(1)在图2,图3中,△是的“旋补三角形”, 是的“旋补中线”.
①如图2,当为等边三角形,且时,则长为 3 .
②如图3,当,且时,则长为 .
猜想论证
(2)在图1中,当为任意三角形时,猜想与的数量关系,并给予证明.(如果你没有找到证明思路,可以考虑延长或延长,
拓展应用
(3)如图4,在四边形中,,,,以为边在四边形内部作等边,连接,.若是的“旋补三角形”,请直接写出的“旋补中线”长及四边形的边长.
【解答】解:(1)①如图2中,
是等边三角形,
,
,
,
,,
,
,
,
故答案为3.
②如图3中,
,,
,
,,
△,
,
,
,
故答案为3.5.
(2)结论:.
理由:如图1中,延长到,使得,连接,
,,
四边形是平行四边形,
,
,,
,
,
△,
,
.
(3)如图4中,过点作于,取的中点,连接.
是等边三角形,
,,
,
,
是的“旋补三角形”,
,,
,
,,
,
,
,
,
的“旋补中线”长,
,
,
也是的“旋补三角形”,
.
3.(2020•汇川区模拟)我们定义:如图1、图2、图3,在中,把绕点顺时针旋转得到,把绕点逆时针旋转得到,连接,当时,我们称△是的“旋补三角形”,△ 边上的中线叫做的“旋补中线”,点叫做“旋补中心”.图1、图2、图3中的△均是的“旋补三角形”.
(1)①如图2,当为等边三角形时,“旋补中线” 与的数量关系为: ;
②如图3,当,时,则“旋补中线” 长为 .
(2)在图1中,当为任意三角形时,猜想“旋补中线” 与的数量关系,并给予证明.
【解答】解:(1)①如图2中,
是等边三角形,
,
,
,
,,
,
,
,
故答案为.
②如图3中,
,,
,
,,
△,
,
,
,
故答案为4.
(2)结论:.
理由:如图1中,延长到,使得,连接,
,,
四边形是平行四边形,
,
,,
,,
△,
,
.
4.(2020•海淀区校级模拟)小明研究了这样一道几何题:如图1,在中,把点顺时针旋转得到,把绕点逆时针旋转得到,连接.当时,请问△边上的中线与的数量关系是什么?以下是他的研究过程:
特例验证:
(1)①如图2,当为等边三角形时,与的数量关系为 ;
②如图3,当,时,则长为 .
猜想论证:
(2)在图1中,当为任意三角形时,猜想与的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形,,,,,,在四边形内部是否存在点,使与之间满足小明探究的问题中的边角关系?若存在,请画出点的位置(保留作图痕迹,不需要说明)并直接写出的边上的中线的长度;若不存在,说明理由.
【解答】解:(1)①是等边三角形,
,,
,
,
,
,
,
,
,
故答案为:;
②,
,
,
,
在和△中,,
△,
,
,
,
故答案为:4;
(2)与的数量关系:;理由如下:
延长到,使得,连接、,如图1所示:
,,
四边形是平行四边形,
,,
,
,
,
在和△中,,
△,
,
;
(3)存在;作于,作线段的垂直平分线交于,即为点的位置;理由如下:
延长交的延长线于,线段的垂直平分线交于,连接、、,作的中线,连接交于,如图4所示:
,
,
,
在中,,,,
,,,
在中,,,,
,
,
,
,
,
,
是线段的垂直平分线,
,,
在中,,,
,
,
,
,
,
,
,
,,
,
在和中,,
,
,
,
四边形是矩形,
,
,
是等边三角形,
,
,
,
,
与之间满足小明探究的问题中的边角关系;
在中,,,,
.
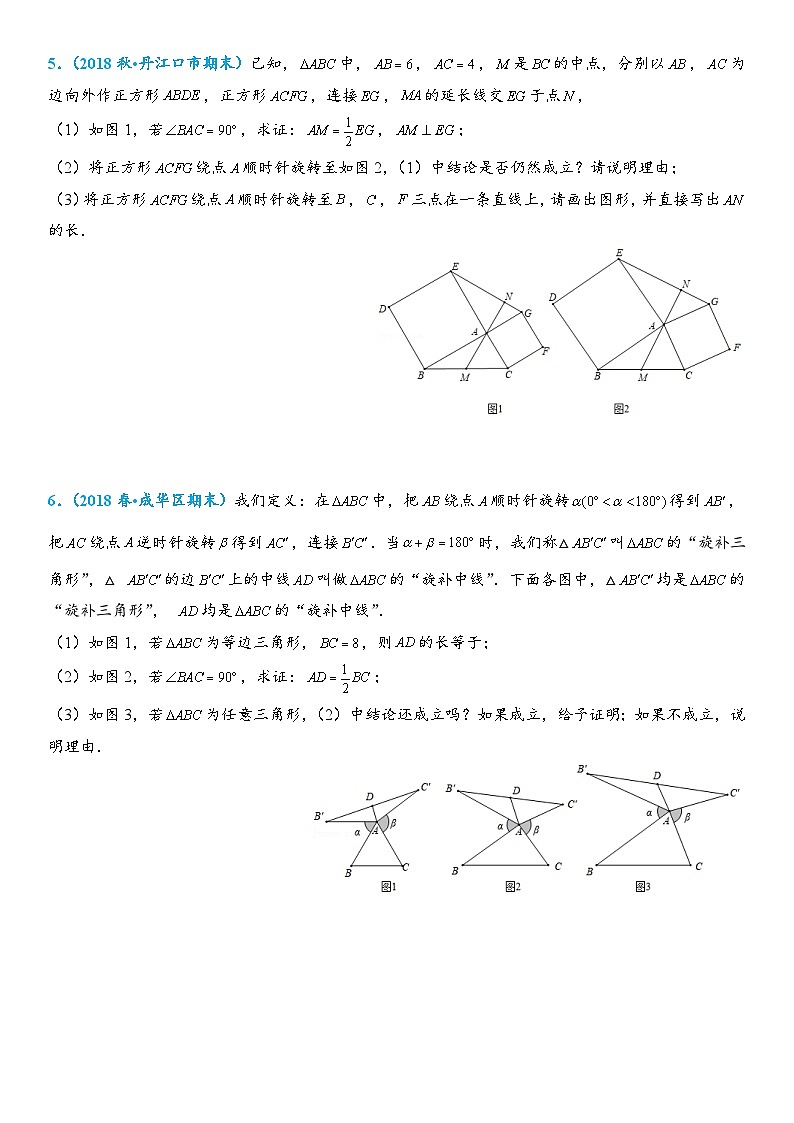
5.(2018秋•丹江口市期末)已知,中,,,是的中点,分别以,为边向外作正方形,正方形,连接,的延长线交于点,
(1)如图1,若,求证:,;
(2)将正方形绕点顺时针旋转至如图2,(1)中结论是否仍然成立?请说明理由;
(3)将正方形绕点顺时针旋转至,,三点在一条直线上,请画出图形,并直接写出的长.
【解答】(1)证明:方法一:如图1中,
四边形,四边形均为正方形,
,
且,,
在和中,
,
,
,,
又是的中点,
,
,
,
,
.
方法二:如图,延长至点,使,连接.
在和中,
,
,
,,
,
四边形,四边形均为正方形,
,
且,,
,
在和中,
,
,
,,
,
,
,为中点,
,
.
(2)如图3中,结论不变.
理由:在和中,
,
,
,,
,
,
四边形,四边形均为正方形,
,
,
,
且,,
,
在和中,
,
,
,,
,
,
为中点,
,
.
(3)①如图中,当点在的延长线上时,作于.
易证:,可得,
在中,,,
,
,
,
.
②如图中,当点在线段上时,同法可得
综上所述,的值为.
6.(2018春•成华区期末)我们定义:在中,把绕点顺时针旋转得到,把绕点逆时针旋转得到,连接.当时,我们称△叫的“旋补三角形”,△ 的边上的中线叫做的“旋补中线”.下面各图中,△均是的“旋补三角形”, 均是的“旋补中线”.
(1)如图1,若为等边三角形,,则的长等于;
(2)如图2,若,求证:;
(3)如图3,若为任意三角形,(2)中结论还成立吗?如果成立,给予证明;如果不成立,说明理由.
【解答】解:(1)如图1中,
是等边三角形,
,
,
,
,,
,
,
,
(2)证明:如图2中,
绕点旋转得到,绕点旋转得到,
,,
,,,
,
,
△
,
是△边上的中线,.
.
.
(3)结论成立.
理由:如图3中,延长到,使得,连接,.
,
,,
四边形是平行四边形,
,
,,
,,
△
,
.
7.(2018春•南京期末)将的边绕点顺时针旋转得到,边绕点逆时针旋转得到,,连接,作△的中线.
【初步感知】
(1)如图①,当,时,的长为 2 ;
【探究运用】
(2)如图②,为任意三角形时,猜想与的数量关系,并证明.
【应用延伸】
(3)如图③,已知等腰,,延长到,延长到,使,将绕点顺时针旋转一周得到△,连接、,若,求的长度(用含、的代数式表示).
【解答】(1)解:,
,
,
,
,,
△,
,
是直角三角形△斜边的中线,
.
故答案为2.
(2)证明:如图①中,延长到,使得.连接,.
,,
四边形是平行四边形,
,,
,
,
,
,
,
△,
,
.
(3)①如图②中,作的中线.
在中,,
,
在中,,
由(2)可知:.
②如图③中,作的中线,延长到,使得,则四边形是平行四边形,
,,
,
,
,
,
,
,
△,
,
由①可知,,
.
8.(2022秋•白云区校级期末)(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在中,,,直线经过点,直线,直线,垂足分别为点、.证明:.
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在中,,、、三点都在直线上,并且有,其中为任意锐角或钝角.请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过的边、向外作正方形和正方形,是边上的高,延长交于点,求证:是的中点.
【解答】解:(1)如图1,
直线,直线,
,
,
,
在和中,
,
,
,,
;
(2).
如图2,
证明如下:
,
,
,
在和中.
.
,
,,
(3)如图3,
过作于,的延长线于.
由(1)和(2)的结论可知
在和中,
,
,
,
是的中点.
9.(2020秋•南川区校级期中)已知:和均为等腰直角三角形,.连接,,点为中点,连接.
(1)如图1所示,若,,求的长.
(2)将绕点旋转一定的角度到图2,
求证:且.
【解答】(1)解:如图1中,
与为等腰直角三角形,,
,,
,,
由勾股定理可得:,,
在中.
在中,是的中点,则,
(2)证明:如图2中,延长到,使得,连接,
,,,
,
,,
,
,
,
在和中,
,
,
.
.
由,知
,
.
10.(2020秋•鼓楼区校级期中)【感知】如图①,在四边形中,,点在边上,,且,求证:.
【探究】如图②,在四边形中,,点在边上,点在边的延长线上,,且,,连接交于点.求证:.
【拓展】如图③,点在四边形内,十,且,,过作交于点,若,延长交于点.求证:.
【解答】证明:(1),
,
,
,
,
在和中,
,
,
,,
;
(2)如图②,过点作于,
由(1)可知,
,
同(1)可得,,
,
,
在和中,
,
,
;
(3)如图③,在的延长线上取点,使,在上取点,使,连接、,
十,十,,
,
在和中,
,
,
,,
同理可得,,
,,
,
,,
,
在和中,
,
,
.
11.(2020•黑龙江)以的两边、为边,向外作正方形和正方形,连接,过点作于,延长交于点.
(1)如图①,若,,易证:;
(2)如图②,;如图③,,(1)中结论,是否成立,若成立,选择一个图形进行证明;若不成立,写出你的结论,并说明理由.
【解答】解:(1)证明:,,
,
,
,
,
同理,
,
四边形和四边形为正方形,
,
.
(2)如图1,时,(1)中结论成立.
理由:过点作交的延长线于,过点作于,
四边形是正方形,
,,
,
,
,
,
在和中,
,
,
,
同理可得:,
,
在和中,
,
,
.
如图2,时,(1)中结论成立.
理由:过点作交的延长线于,过点作于,
四边形是正方形,
,,
,
,
,
,
在和中,
,
,
,
同理可得:,
,
在和中,
,
,
.
12.(2020秋•亭湖区期中)【感知】
如图1,在四边形中,,点在边上,且满足是等腰直角三角形,.求证:.
【探究】
如图2,在四边形中,,点在边上,且满足是等腰直角三角形,,点在边的延长线上,连接,以为直角边作等腰,过点作,垂足为,连接交于点.求证:.
【拓展】
如图3,点在四边形内,,且,,过点作交于点,使,延长交于点.试探究与之间的数量关系,并说明理由.
【解答】【感知】证明:是等腰直角三角形,,
,,
,
,
在和中,
,
;
【探究】证明:由感知可知,,
,
,,
,
,
,
在和中,
,
,
;
【拓展】解:,
理由如下:在的延长线上取点,使,在上取点,使,连接、,
,,,
,
在和中,
,
,
,,
同理可得,,
,,
,
,,
,
在和中,
,
,
,
.
13.如图:分别以的边、为边,向三角形的外侧作正方形和正方形,为上的高,延长交于点,求证:为的中点.
【解答】解:过点作的延长线于,过点作于,如图所示:
四边形是正方形,
,,
,
,
,
,
在和中,,
,
,
同理可得:,
,
在和中,,
,
,
为的中点.
14.(2020•桥西区模拟)如图①,在中,把绕点顺时针旋转得到,把绕点逆时针旋转得到,连接,当时,我们称△是的旋补三角形,△边上的中线叫做的旋补中线.
如图②,当为等边三角形时,△是的旋补三角形,是旋补中线,与的数量关系为: ;当时,则长为 .
【解答】解:如图②中,
是等边三角形,
,
,
,
,,
,
,
,
,
,
,
,
故答案为:,.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2023/10/3 0:45:10;用户:微信用户;邮箱:rFmNt0ALlhXWmlRPd3BByUm_TL4@;学号:47883804
2024年中考数学几何模型专项复习讲与练 模型20 轴对称——婆罗摩笈多模型-原卷版+解析: 这是一份2024年中考数学几何模型专项复习讲与练 模型20 轴对称——婆罗摩笈多模型-原卷版+解析,共27页。试卷主要包含了垂直 中点,中点 垂直等内容,欢迎下载使用。
中考数学几何模型专项复习 模型20 轴对称——婆罗摩笈多模型-(原卷版+解析): 这是一份中考数学几何模型专项复习 模型20 轴对称——婆罗摩笈多模型-(原卷版+解析),共26页。试卷主要包含了垂直 中点,中点 垂直等内容,欢迎下载使用。
婆罗摩笈多模型讲义+练习含参考答案: 这是一份婆罗摩笈多模型讲义+练习含参考答案,共6页。












