2024年中考数学压轴题专项练习—三角形中的新定义问题

这是一份2024年中考数学压轴题专项练习—三角形中的新定义问题，文件包含74三角形中的新定义问题答案docx、74三角形中的新定义问题docx等2份试卷配套教学资源，其中试卷共56页， 欢迎下载使用。
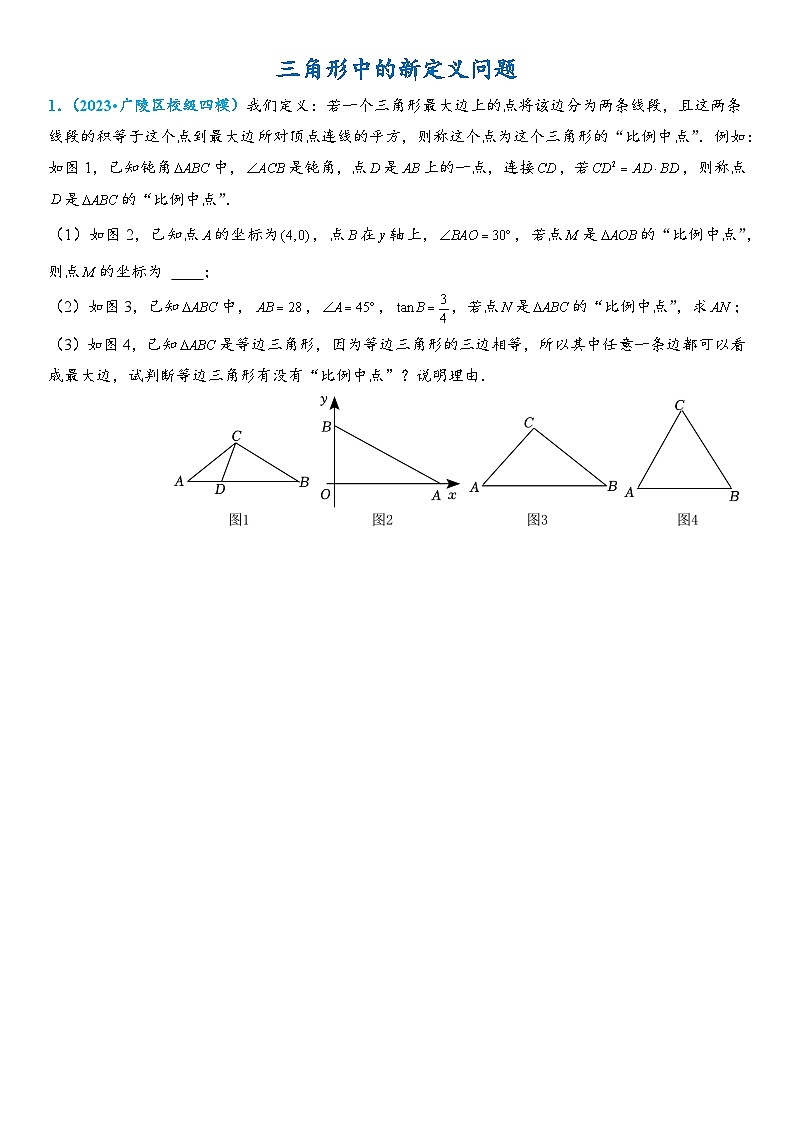
（1）如图2，已知点的坐标为，点在轴上，，若点是的“比例中点”，则点的坐标为 或 ；
（2）如图3，已知中，，，，若点是的“比例中点”，求；
（3）如图4，已知是等边三角形，因为等边三角形的三边相等，所以其中任意一条边都可以看成最大边，试判断等边三角形有没有“比例中点”？说明理由．
【解答】解：（1）如图2所示，
过点作于点，连接，
已知点的坐标为，点在轴上，，
，
设，则，
，，
在中，，
点是的“比例中点”，
，
，
解得：或，
或，
当时，，，即；
当时，，，即；
故答案为：或；
（2）点是的“比例中点”，
，
设，则，
如图3所示，过点作于点，
中，，，，
，，
设，则，
，
，
解得：，
，，
，
，
解得：或，
或18；
（3）等边三角形没有“比例中点”．理由如下：
设点是的“比例中点”，设等边三角形的边长为，
，
设，则，
如图4所示，过点作于点，
中，，
，，，
，
，
，
此方程无解，
等边三角形没有“比例中点”．
2．（2022秋•泰兴市期中）我们类比黄金分割点给出如下定义：如图点、、在同一条直线上，，则称点为，的“银杏点”．特别地，若为的中点时，则为，的“银杏点”， 也为，的“银杏点”．
（1）已知，点在线段上，若点为，的“银杏点”，则 2 ．
（2）如图，为的重心，则下列说法正确的是 （填序号）．
①为，的“银杏点”；
②为，的“银杏点”；
③为，的“银杏点”；
④为，的“银杏点”．
（3）如图，在中，．若，．
①求的长；
②当点在边上，且、、中有一点为其它两点的“银杏点”．点在直线上，且．求的长．
【解答】解：（1）点为，的“银杏点”，
，
，
，
，
故答案为：2；
（2）如图1，连接，
点，分别是，的中点，
，且，
，
点是，的“银杏点”，点是，的“银杏点”故①正确，②不正确；
点是的中点，
为，的“银杏点”， 也为，的“银杏点”；故③不正确；
点是的中点，
为，的“银杏点”， 也为，的“银杏点”；故④正确；
故答案为：①④；
（3）①在中，．
．
设，则，
，
，
，即，
，．
②根据题意可知，需要分三种情况：
Ⅰ、如图2，当点为的中点时，即点为，的“银杏点”或点为，的“银杏点”；
此时，
，
，，
，即，
，，
，
，即，
解得，
；
Ⅱ、当点为，的“银杏点”，有，
，，
过点作于点，
，
，
，
，即，
，，
，
，
当，时，
则有，
，即，
，
；
Ⅲ、如图4，当点为，的“银杏点”，则有，
，，
过点作于点，
，
，
，
，即，
，，
，
，
若，则需要分两种情况：
当点在的右侧时，由上可知，，
此时，时，
，
，即，
，
；
当在的左侧时，记为，
，
过点作于点，则为的中点，四边形是矩形，
，，
，
，
，
综上，符合题意的的值为：1或17或或．
3．（2022•任城区三模）我们定义：等腰三角形中底边与腰的比叫做顶角的正对．如图①在中，，顶角的正对记作，这时．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：
（1） 1 ．
（2） ．
（3）如图②，已知，其中为锐角，试求的值．
【解答】解：（1）；
（2）；
（3）设，，则，
在上取，作于点，如图所示：
则，，
，，
．
4．（2021秋•鼓楼区校级期末）定义1：如图1，若点在直线上，在的同侧有两条以为端点的线段、，满足，则称和关于直线满足“光学性质”；
定义2：如图2，在中，的三个顶点、、分别在，、上，若和关于满足“光学性质”， 和关于满足“光学性质”， 和关于满足“光学性质”，则称为的光线三角形．
阅读以上定义，并探究问题：
在中，，，三个顶点、、分别在、，上．
（1）如图3，若，和关于满足“光学性质”，求的度数；
（2）如图4，在中，作于，以为直径的圆分别交，于点，．
①证明：为的光线三角形；
②证明：的光线三角形是唯一的．
【解答】（1）解：如图3中，，，
，
，
，
和关于满足“光学性质”，
，
；
（2）①证明：如图4中，
，，
，
是直径，
，
，
，，
，
，
，
，
，
，
，
，，
，
，关于满足光学性质，
，，
，
，
，
，，
，，
，关于满足光学性质，，关于满足光学性质，
是为的光线三角形；
②证明：由①可知，，，
是顶角为，腰长为的一半的等腰三角形，
是唯一确定的，
的光线三角形是唯一的．
5．（2021•柯城区模拟）定义：若三角形的一条边上的高线与这条边相等，则称这个三角形为“等底高三角形”，这条边叫做等底线，这条边上的高叫做等高线．如图：在，于点，且，则为等底高三角形，叫等底线，叫等高线．
【概念感知】
判断：对的打“”，错的打“”．
（1）等边三角形不可能是等底高三角形．
（2）等底高三角形不可能是钝角三角形．
【概念理解】
若一个等腰三角形为等底高三角形，则此三角形的三边长之比为 ．
【概念应用】
（1）若为等底高三角形，等底线长为2，求三角形的周长的最小值．
（2）若一个等底高三角形的其中一边是另一边的倍，求最小角的正弦值．
【解答】解：【概念感知】
（1），边与高构成直角三角形，斜边不可能等于直角边；
（2），如图1，高在一边的延长线上即可．
【概念理解】分两种情况：第一种情况如图，底边上的高等于底边时，
设，则，
，
在中，，
．
第二种情况，如图，等腰直角三角形中，两个腰分别为底和高时，
设，则，
在中，，
．
【概念应用】
（1）如图3，，设，则，
在中，，
在中，，
．
是点到的距离，
是点到的距离，
如图4，作关于轴的对称点，
则到距离即为所求．
．
（2）如图1，设．
，
，
设，
，
，
．
，
，
又、均为锐角，为钝角，且．
最小，．
故答案为．
6．（2021•宁波模拟）在三角形的三边中，若其中两条边的积恰好等于第三边的平方，我们把这样的三角形叫做有趣三角形，这两条边的商叫正度，记为．
（1）求证：正度为1的有趣三角形必是等边三角形．
（2）如图①，四边形中，，平分，，求证：是有趣三角形．
（3）如图②，菱形中，点，是对角线的三等分点，．延长到，使．
求证：，，是具有相同正度的有趣三角形．
【解答】证明：（1）不妨假设．
正度为1，
，
，
，
，
是等边三角形；
（2）如图①中，，
，，
平分，
，
，
，
，
，
，
，
，
是有趣三角形；
（3）如图②中，点，是对角线的三等分点，，
，
，
四边形是菱形，
，
，
，
，
，
，
，，
，
，
，
，
，
，
，
，
，
是有趣三角形，
，
，
，
，
，
，
是有趣三角形，
，
，
，
，
，
，
是有趣三角形，
的正度，的正度，的正度，
，，是具有相同正度的有趣三角形．
7．（2021秋•西城区校级期中）对于平面直角坐标系内的任意两点，，，，定义它们之间的“直角距离”为．
对于平面直角坐标系内的任意两个图形，，给出如下定义：为图形上任意一点，为图形上任意一点，如果，两点间的“直角距离”有最小值，那么称这个最小值为图形，间的“直角距离”，记作．
（1）已知，，则 3 ， ；
（2）已知，，若，则的取值范围是 ；
（3）已知，若坐标平面内的点满足，则在图中画出所有满足条件的点所构成的图形，该图形的面积是 ；
（4）已知，，直线过点且垂直于轴，若直线上存在点满足，，，则的取值范围是 ．
【解答】解：（1）由题意，，，
，，，
故答案为：3，1；
（2）由题意，
当时，满足条件，
或；
故答案为：或；
（3）如图，满足条件的点在正方形上，面积．
故答案为：2．
（4）设．
，，，
，
当或时，无解，此时不存在满足条件的点，
当时，，
当时，，解得，
当时，，
，
，
，
当时，，，
综上所述，满足条件的的值为：，
故答案为：．
8．（2021秋•北仑区期中）定义：若连结三角形一个顶点和对边上一点的线段能把该三角形分成一个等腰三角形和一个直角三角形，我们称这条线段为该三角形的智慧线，这个三角形叫做智慧三角形．
（1）如图1，在智慧三角形中，，为该三角形的智慧线，，，则长为 2 ，的度数为 ．
（2）如图2，为等腰直角三角形，，是斜边延长线上一点，连结，以为直角边作等腰直角三角形（点，，按顺时针排列），，交于点，连结，．当时，求证：是的智慧线．
（3）如图3，中，，．若是智慧三角形，且为智慧线，求的面积．
【解答】（1）解：，
，
，，
，
是智慧三角形，
是等腰直角三角形，
，，
故答案为：2，
（2）证明：如图2中，，
，
在和中，
，
，
，
，
，
，
，，
，
，
是等腰三角形，
是直角三角形，
是智慧三角形；
（3）解：如图3中，过点作于点．
有两种情形：当时，或当时，，是智慧三角形．
，，
，
，
，
，
，
，
，，
，，
，
，
，
，
，
，
，
解法二：设，，
则有，
解得，
可得，
综上所述，满足条件的的面积为16或．
9．（2020•岳麓区校级二模）定义：在中，若有两条中线互相垂直，则称为中垂三角形，并且把叫做的方周长，记作，即．
（1）如图1，已知是中垂三角形，，分别是，边上的中线，若，求证：是等腰直角三角形；
（2）如图2，在中垂三角形中，，分别是边，上的中线，且于点，试探究的方周长与之间的数量关系，并加以证明；
（3）如图3，已知抛物线与轴正半轴相交于点，与轴相交于点，经过点的直线与该抛物线相交于点，与轴负半轴相交于点，且，连接交轴于点．
①求证：是中垂三角形；
②若为直角三角形，求的方周长的值．
【解答】（1）证明：，，分别是，边上的中线，
，，
，
，
．
是中垂三角形，且，
，
是等腰直角三角形．
（2）．
证明：如图，连接．
，分别是边，上的中线，
，，，
，，．
在中，，
在中，，
，
．
（3）①证明：在中，当时，，
点．
时，，
整理得，
解得（舍，，
点．
，
，
将代人，
解得（舍，，
．
由点，可知，是的中点．
又，
，都是的中线．
又，
，
是中垂三角形．
②解法一：由点，，可得，，，
，
．
当时，，
解得（负值舍去），
点，
．
当时，，
解得（负值舍去），
点，
．
综上所述，的方周长的值为144或288．
解法二：由点，，，
点是的中点，点是的中点，
点，．
，
．
当时，在 中，由射影定理得，
，解得（负值舍去），
点，
．
当时，在中，由射影定理得，
，解得（负值舍去），
点，
．
综上所述，的方周长的值为144或288．
10．（2019•义乌市模拟）定义：若中，其中一个内角是另一个内角的一半，则称为“半角三角形”．
（1）若为半角三角形，，则其余两个角的度数为 ，或， ．
（2）如图1，在中，，点在边上，以为折痕，将向上翻折，点恰好落在边上的点，若，求证：为半角三角形；
（3）如图2，以的边为直径画圆，与边交于，与边交于，已知的面积是面积的4倍．
①求证：．
②若是半角三角形，直接写出的度数．
【解答】解：（1）为半角三角形，，
，或，或，，
其余两个角的度数为，或，，
故答案为，或，．
（2）如图1中，
平行四边形中，，
，
由翻折可知：，
，
，
，
，即是半角三角形．
（2）①如图2中，连接．
是直径，
，
，，
，
，即，
在中，，
，
．
②是半角三角形，，
或或或．
11．（2018秋•武侯区校级期中）阅读下面的材料，然后解答问题：
我们新定义一种三角形，两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形．
理解：
①根据奇异三角形的定义，请你判断：等边三角形一定是奇异三角形吗？ 是 （填“是”或“不是”
②若某三角形的三边长分别为1、、2，则该三角形 （填“是”或“不是” 奇异三角形．
探究：
在中，两边长分别是、，且，，则这个三角形是否是奇异三角形？请说明理由．
拓展：
在中，，，，，且，若是奇异三角形，求．
【解答】解：①设等边三角形的边长为，
，
等边三角形一定是奇异三角形，
故答案为：是；
②，
该三角形是奇异三角形，
故答案为：是；
探究：当为斜边时，，不是奇异三角形；
当为斜边时，，
，
是奇异三角形；
拓展：中，，
，
，
，，
是奇异三角形，
，
，
，
，
，
．
12．（2016秋•余姚市期末）定义：如图1，，在的边上，若是等边三角形则称可内嵌，叫做的内嵌三角形．
（1）直角三角形 不一定 可内嵌．（填写“一定”、“一定不”或“不一定”
（2）如图2，在中，，是的内嵌三角形，试说明是否成立？如果成立，请给出证明；如果不一定成立，请举例说明．
（3）在（2）的条件下，如果，，求的内嵌的边长
【解答】解：（1）当直角三角形是等腰直角三角形时可内嵌，
直角三角形不一定可内嵌．
（2）是的内嵌三角形，
是正三角形，
，
在和中，
，
，
即．
（3）设，
，，
，
，
，
即，
同理，
，
，
解得，
，
的内嵌的边长是．
故答案为：不一定．
13．（2016秋•宜兴市校级期中）定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．
（1）请你在图1中用两种不同的方法画出顶角为的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）
（2）中，，和是的三分线，点在边上，点在边上，且，，设，试画出示意图，并直接写出所有可能的值；
（3）如图2，中，，，，请画出的三分线，并求出三分线的长．
【解答】解：（1）如图所示：
（2）如图所示：
①当时，
，
；
②当时，
，
；
（3）第一种情况，如图所示，、就是所求的三分线．
设，则，，
此时，，
设，，
，
，①
，
，②
由①和②解得或（舍去），
，，
即三分线的长分别为和．
第二种情况，如图所示，、就是所求的三分线．
设，则，，
在上取点使得，则，，
，
在上截取，则，
，
，
，
即三分线的长分别为1和2．
第三种情况，如图所示，，就是所求的三分线．
连接，过作于，
由，，，可得，
，即平分，
由角平分线定理可得，，
设，则，，
，
解得（负值已舍去），经检验是所列方程的解，
，，
，，
，，
，
，
解得，
即三分线的长分别为和．
14．（2016秋•江阴市校级月考）定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．
性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．
理解：如图①，在中，是边上的中线，那么和是“友好三角形”，并且．
应用：如图②，在矩形中，，，点在上，点在上，，与交于点．
（1）求证：和是“友好三角形”；
（2）连接，若和是“友好三角形”，求四边形的面积．
探究：在中，，，点在线段上，连接，和是“友好三角形”，将沿所在直线翻折，得到△，若△与重合部分的面积等于面积的，求出的面积．
【解答】应用：（1）证明：四边形是矩形，
，
，
四边形是平行四边形，
，
和是友好三角形．
（2）解：和是友好三角形，
，，
与是友好三角形，
，
，
，
，
．
探究：
解：分为两种情况：①如图1，
．
，
沿折叠和重合，
，
△与重合部分的面积等于面积的，
，
，，
四边形是平行四边形，
，
过作于，
，，
，
即和重合，
，
由勾股定理得：，
的面积是；
②如图2，
．
，
沿折叠和重合，
，
△与重合部分的面积等于面积的，
，
，，
四边形是平行四边形，
，
过作于，
，，
，
；
即的面积是8或．
15．（2023•平谷区二模）在平面直角坐标系中，对于，其中，，给出如下定义：将边绕点逆时针旋转得到线段，连接，与的过点的高线交于点，将点关于直线对称得到点，我们称为的留缘点．
（1）若，，请在图中画出的留缘点，并求出点的坐标；
（2）已知，，若线段上存在的留缘点，求的取值范围．
【解答】解：（1）如图，点即为的留缘点，连接，
，，
，，，
是正三角形，
，
将边绕点逆时针旋转得到线段，
，，
是正三角形，
，
四边形是菱形，
，
，
，
，
点与点关于直线对称，
，．
（2）如图所示，连接、，作、的中垂线，交轴与点、，设、，
点、分别在、的中垂线上，
，，
，，
，，
线段上存在的留缘点，
或．
16．（2022秋•泗阳县期末）概念生成．
我们把两个具有公共底边的等腰三角形称为同底等腰三角形，公共的这条底边称为针准线，称这两个等腰三角形的顶角顶点关于针准线互为穿针点，互为穿针点的两个顶角顶点的连线称为穿针线，若再满足两个顶角的和为，则称这两个顶角顶点关于针准线互为补角穿针点．
例：如图1，四边形中，，，则与称为同底等腰三角形，公共底边称为针准线，顶角顶点与点关于互为穿针点；当时，则称点与点关于互为补角穿针点．
概念理解．
（1）下列说法正确的有 ① ．
①同底等腰三角形的穿针线垂直平分针准线
②如果同底等腰三角形的两个顶角顶点关于针准线互为补角穿针点，则其中一个等腰三角形的腰必垂直于另一个等腰三角形中具有公共端点的腰．
③在图1中，与点关于互为补角穿针点的点有无数个．
（2）如图2，，，，则点与点 关于互为穿针点．
知识应用．
（3）在长方形中，，．如图3，点在边上，点在边上，如果点和点关于针准线互为补角穿针点，求针准线的长．
（4）如图4，中，，，点是平面内一点，如果点与点关于针准线互为补角穿针点，求的长．
【解答】解：（1）①同底等腰三角形的两个顶点均在底边的垂直平分线上，故同底等腰三角形的穿针线垂直平分针准线是正确的，
②如果同底等腰三角形的两个顶角顶点关于针准线互为补角穿针点，当这两个顶点位于针准线的同侧时，则其中一个等腰三角形的腰与另一个等腰三角形中具有公共端点的腰不垂直，故结论②不正确．
③在图1中，与点关于互为补角穿针点的点有2个，故结论③不正确；
故答案为：①．
（2）根据“穿针点”的定义可知：点与点、点与点均关于互为穿针点，
故答案为：或点；
（3）四边形是矩形，
，，，
如图，点和点关于针准线互为补角穿针点，
，
在中，，
，
在中，；
（4）连接交于点，
点与点关于针准线互为补角穿针点，
，，，
在中，，，
，
当点与点在的异侧时，如图，
在和中，
，
，
，，
，
，
，
，即，
，
设，且，则，
，
，
整理得：，
，
；
当点与点在的同侧时，如图，
，
；
综上所述，的长为或．
17．（2022秋•武侯区期末）阅读理解
在平面直角坐标系中，已知点（其中，，点为平面内一点，现给出如下定义：将点先向右平移个单位长度，再向上平移个单位长度，得到点，点关于直线的对称点为．那么我们称点为点关于点的“平对点”．
迁移运用
在平面直角坐标系中，已知点（其中，，点为平面内一点，点为点关于点的“平对点”．完成下列各题：
（1）当，时．
ⅰ如图1，若点的坐标为，请在图中画出点；
ⅱ如图2，若点的坐标为，连接，求的长；
（2）当点在直线左侧时，连接，，若直线与直线相交所形成的锐角为，求线段的长的最小值（用含，的代数式表示）．
【解答】解：（1）①如图：
②点的坐标为，
，
设，
由对称轴可知，，
，
解得（舍或，
，，
；
（2）连接，，，设直线与直线的交点为，与的交点为，
由对称性可知，，，
，
，
△是等腰直角三角形，
设，则，
，
，，
四边形是平行四边形，
，
当时，的长最小，此时点与点重合，
，
的最小值为．
18．（2021秋•青原区期末）我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点．
●特例感知
①等腰直角三角形 是 勾股高三角形（请填写“是”或者“不是” ；
②如图1，已知为勾股高三角形，其中为勾股顶点，是边上的高．若，试求线段的长度．
●深入探究
如图2，已知为勾股高三角形，其中为勾股顶点且，是边上的高．试探究线段与的数量关系，并给予证明；
●推广应用
如图3，等腰为勾股高三角形，其中，为边上的高，过点向边引平行线与边交于点．若，试求线段的长度．
【解答】解：●特例感知：
①等腰直角三角形是勾股高三角形．
故答案为是．
②如图1中，根据勾股定理可得：，，
于是，
．
●深入探究：
如图2中，由可得：，而，
，
即；
●推广应用：
过点向引垂线，垂足为，
“勾股高三角形” 为等腰三角形，且，
只能是，由上问可知①．
又，②．
而③，
，
．
易知与均为等腰三角形，
根据三线合一原理可知．
又，，
，
．
19．（2021秋•石景山区期末）在中，，，点是线段上的一个动点（不与点，重合），过点作直线交于点．给出如下定义：
若在边上存在一点，使得点关于直线的对称点恰好在的边上，则称点是的关于直线的“反称点”．
例如，图1中的点是的关于直线的“反称点”．
（1）如图2，若，点，，，在边上且，，，．在点，，，中，是的关于直线的“反称点”为 、 ；
（2）若点是的关于直线的“反称点”，恰好使得是等腰三角形，求的长；
（3）存在直线及点，使得点是的关于直线的“反称点”，直接写出线段的取值范围．
【解答】解：（1）中，，，
，
点与点关于直线对称，直线，，
，，
直线截得到的含的三角形是等腰直角三角形，
直线与边的交点到点的距离等于，
，，，，，
点关于直线对称，，
点在的外部，
同理，点关于直线对称，，点在的边上，
点关于直线对称，，点在的内部，
，则点与点重合，，点在的边上，
、不是的关于直线的“反称点”， 、是的关于直线的“反称点”，
故答案为：、；
（2）中，，，
，
点与点关于直线对称，直线，，
，，
，
若是等腰三角形，
①若为底边，是等腰直角三角形，如图1所示：
则，
，
，
，
，
，
是的中点，
是的中位线，
是的中点，
；
②若为腰且为顶角，如图2所示：
则，
在中，，，
；
③若为腰且为顶角，则点与点重合，点与点重合，如图3所示：
；
综上所述，的长为3或或6；
（3）由（1）知，时，等于2倍的到的距离时，点在边上，
时，到的距离小于等于3时，点在边上，
当到的距离大于3时，点在的外部，
等于到的距离，
．
20．（2022秋•秦淮区校级月考）定义：如图①，若线段沿点、能折成一个直角三角形（其中、两点重合），则称点、是线段的“△”折点；若是直角顶点，则称为线段的“”
折点．
（1）当，，时，求证：点是线段的“”折点；
（2）若点、是线段的“△”折点，且为直角边，，，求的长；
（3）如图②，，，，将线段沿、、三点折成含2个直角的四边形（其中、两点重合），且、不是线段的“”折点．直接写出的长度．
【解答】（1）证明：，，，
，
是直角三角形，为直角顶点，
点是线段的“”折点；
（2）解：点、是线段的“△”折点，且为直角边，
设，则在中，，则，
有两种情况：
①，
即，
解得：；
②，
即，
解得：．
综上所述：的长为3或5；
（3）由图知，，，，设，则，
又、不是线段的“”折点，则，；，；，可能为“”折点，
即分三种情况：①，为线段的“”折点，
则有，
解得：；
②，为线段的“”折点，
则有，
解得：；
③，为线段的“”折点，
则有，
解得：．
综上所述：的长度为2或或．