

高一物理下学期期末复习精细讲义(人教2019)第5讲 功和功率(原卷版+解析)
展开——划重点之精细讲义系列
知识1:功
1.做功的两个要素
力和物体在力的方向上发生的位移.
2.公式:W=Flcs α
(1)该公式只适用于恒力做功.
(2)α是力与位移方向的夹角,l为物体对地的位移.
3.功的正负的意义
(1)功是标量,但有正负之分,正功表示动力对物体做功,负功表示阻力对物体做功.
(2)一个力对物体做负功,往往说成是物体克服这个力做功(取绝对值).
知识2:功率
1.定义
功与完成这些功所用时间的比值.
2.物理意义
描述做功的快慢.
3.公式
(1)P=eq \f(W,t),P为时间t内的平均功率.
(2)P=Fvcs α(α为F与v的夹角)
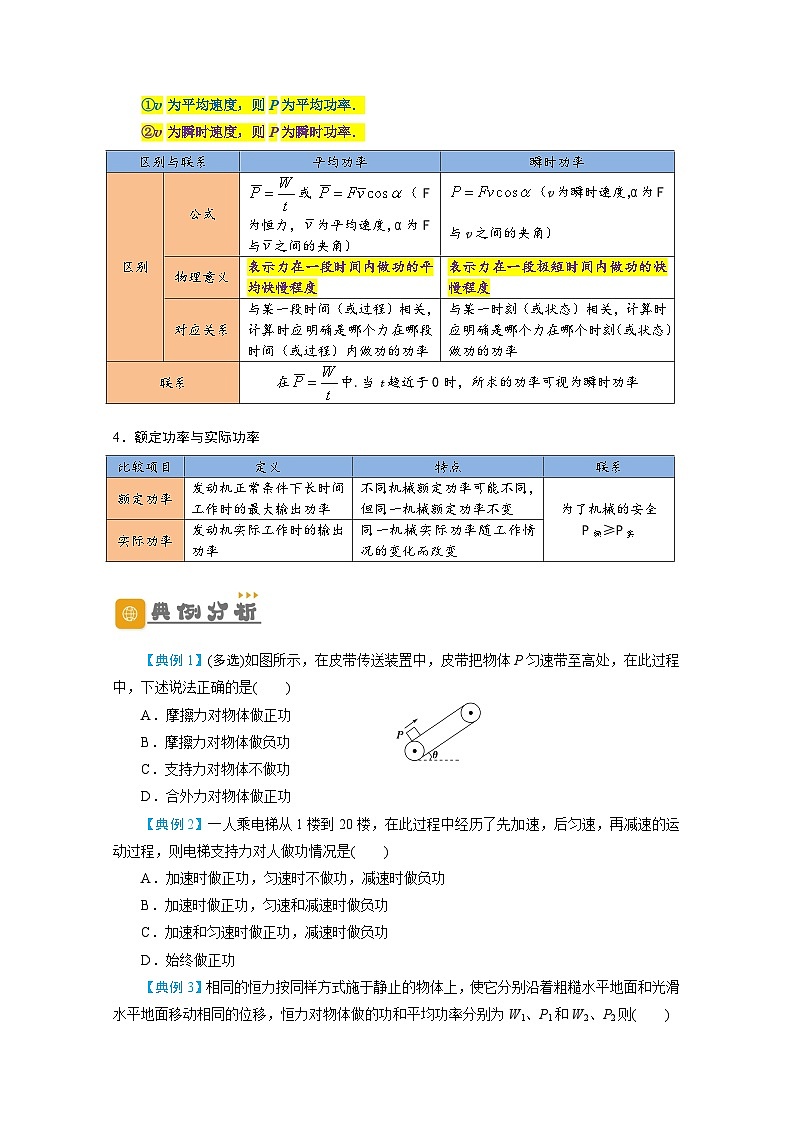
①v为平均速度,则P为平均功率.
②v为瞬时速度,则P为瞬时功率.
4.额定功率与实际功率
【典例1】(多选)如图所示,在皮带传送装置中,皮带把物体P匀速带至高处,在此过程中,下述说法正确的是( )
A.摩擦力对物体做正功
B.摩擦力对物体做负功
C.支持力对物体不做功
D.合外力对物体做正功
【典例2】一人乘电梯从1楼到20楼,在此过程中经历了先加速,后匀速,再减速的运动过程,则电梯支持力对人做功情况是( )
A.加速时做正功,匀速时不做功,减速时做负功
B.加速时做正功,匀速和减速时做负功
C.加速和匀速时做正功,减速时做负功
D.始终做正功
【典例3】相同的恒力按同样方式施于静止的物体上,使它分别沿着粗糙水平地面和光滑水平地面移动相同的位移,恒力对物体做的功和平均功率分别为W1、P1和W2、P2则( )
A.W1>W2 P1>P2 B.W1=W2 P1
考点1:功的正负判断方法
1.根据夹角判断
2.从能的转化角度来进行判断
此法常用于判断相互联系的两个物体之间的相互作用力做功的情况.
例如,车M静止在光滑水平轨道上,球m用细线悬挂在车上,由中的位置无初速地释放,则可判断在球下摆过程中绳的拉力对车做正功.因为绳的拉力使车的动能增加了.又因为M和m构成的系统的机械能是守恒的,M增加的机械能等于m减少的机械能,所以绳的拉力一定对球m做负功.
【典例1】人造地球卫星在椭圆轨道上运行,由中的a点运动到b点的过程中( )
A.万有引力对卫星做正功
B.万有引力对卫星做负功
C.万有引力对卫星先做正功,再做负功
D.万有引力对卫星一直不做功
【典例2】(多选)如图所示,重球m用一条不可伸长的轻质细线拴住后悬于O点,重球置于一个斜面不光滑的斜劈M上,用水平力F向左推动斜劈M在光滑水平桌面上由位置甲匀速向左移动到位置乙,在此过程中,正确的说法是( )
A.M、m间的摩擦力对m不做功
B.M、m间的摩擦力对m做负功
C.F对M所做的功与m对M所做的功的绝对值相等
D.M、m间的弹力对m做正功
1.作用力与反作用力做功特点
作用力和反作用力虽然等大反向,但由于其分别作用在两个物体上,产生的位移效果无必然联系,故作用力和反作用力的功不一定一正一负,大小也不一定相等.
2.静摩擦力做功的特点
(1)静摩擦力可以做正功,也可以做负功,还可以不做功。
(2)在静摩擦力做功的过程中,静摩擦力起着传递机械能的作用,没有机械能转化为其他形式的能。
(3)相互摩擦的系统内,一对静摩擦力做功的代数和总为零。
3.滑动摩擦力做功的特点
(1)滑动摩擦力可以做正功,也可以做负功,还可以不做功。
(2)在一对滑动摩擦力做功的过程中,能量的转化有两个方面:一是相互摩擦的物体之间机械能的转移;二是机械能转化为内能,转化为内能的数值等于滑动摩擦力与相对路程的乘积。
(3)滑动摩擦力、空气阻力等做的功,在曲线运动或往返运动中等于力和路程(不是位移)的乘积。
考点2:功的计算
1.恒力做的功:直接用W=Flcs α计算.
2.合外力做的功
方法一:先求合外力F合,再用W合=F合lcs α求功.
方法二:先求各个力做的功W1、W2、W2、……,再应用W合=W1+W2+W3+……求合外力做的功.
3.变力做的功——将变力做功转化为恒力做功
(1)平均值法
当力的方向不变,大小随位移按线性规律变化时,可先求出力对位移的平均值,再由计算功,如弹簧弹力做的功。
(2)分段法
力在全程是变力,但在每一个阶段是恒力,这样就可以先计算每个阶段的功,再利用求和的方法计算整个过程中变力做的功。
(3)微元法
将运动过程无限分割,每一小段就可看成恒力做功,然后把各小段恒力做的功求出来,再求出代数和,即为全过程该变力所做的功。这种处理问题的方法具有普遍的适用性。但在高中阶段该方法主要用于处理大小不变、方向与运动方向始终相同或相反的变力做功的问题。如滑动摩擦力、空气阻力做功就属于这种类型。不难得出,这种情况下,力对物体做功的绝对值等于力与物体运动路程的乘积。
(4)转换研究对象法
如图所示,人站在地上以恒力拉绳子,使小车向左运动,求绳子拉力对小车所做的功。绳子拉力对小车来说是个变力(大小不变,方向改变),但仔细研究,发现人拉绳的力却是恒力,于是转换研究对象,用人拉绳的力所做的功来求绳子拉力对小车做的功。
2.图像法
如果参与做功的变力方向与位移方向始终共线而大小随位移变化,我们可作出该力随位移变化的图像,如图所示,这时变力做的功 W可用 F-l图线与l轴所围成的图形的面积来表示。l轴上方的面积表示力对物体做的正功的多少,l轴下方的面积表示力对物体做的负功的多少。
【典例1】如图所示,建筑工人通过滑轮装置将一质量是100 kg的料车沿30°角的斜面由底端匀速地拉到顶端,斜面长L是4 m,若不计滑轮的质量和各处的摩擦力,g取10 N/kg,求这一过程中
(1)人拉绳子的力做的功;
(2)物体的重力做的功;
(3)物体受到的合力对物体做的总功.
【典例2】人在A点拉着绳通过一定滑轮吊起质量m=50 kg的物体,如图所示,开始时绳与水平方向的夹角为60°.当人匀速提起重物由A点沿水平方向运动l=2 m而到达B点时,绳与水平方向成30°角.则人对绳的拉力做了多少功?
公式W=Flcs α中位移“l”的意义:
(1)力对平动的物体(可看作质点)做功,“l”为物体上每一点的位移(即受力质点对地的位移).
(2)若受力物体发生转动或形变,“l”应取作用点的位移.
(3)“l”的取值一般以大地为参考系.
考点3:功率的计算
1.平均功率的计算方法
(1)利用eq \x\t(P)=eq \f(W,t).
(2)利用eq \x\t(P)=F·eq \x\t(v)cs θ,其中eq \x\t(v)为物体运动的平均速度,F为恒力.
2.瞬时功率的计算方法
(1)利用公式P=F·vcs θ,其中v为t时刻的瞬时速度.
(2)利用公式P=F·vF,其中vF为物体的速度v在力F方向上的分速度.
(3)利用公式P=Fv·v,其中Fv为物体受的外力F在速度v方向上的分力.
【典例1】如图所示,细线的一端固定于O点,另一端系一小球.在水平拉力作用下,小球以恒定速率在竖直平面内由A点运动到B点.在此过程中拉力的瞬时功率变化情况是( )
A.逐渐增大 B.逐渐减小
C.先增大,后减小 D.先减小,后增大
【典例2】如图甲所示,滑轮质量、摩擦均不计,质量为2 kg的物体在F作用下由静止开始向上做匀加速运动,其速度随时间的变化关系如图乙所示,g取10 m/s2.
求:(1)4 s末力F的瞬时功率;
(2)4 s内F做功的平均功率.
求力做功的功率时应注意的问题
(1)首先要明确所求功率是平均功率还是瞬时功率,对应于某一过程的功率为平均功率,对应于某一时刻的功率为瞬时功率.
(2)求功率大小时要注意F与v方向间的夹角α对结果的影响.
(3)用P=F·eq \x\t(v)cs α求平均功率时,eq \x\t(v)应容易求得,如求匀变速直线运动中某力的平均功率.
机车的两种启动模型的分析
1.模型综述
物体在牵引力(受功率和速度制约)作用下,从静止开始克服一定的阻力,加速度不变或变化,最终加速度等于零,速度达到最大值.
2.两种模型的比较
(1)两种启动方式的比较
(2)三个重要关系式
(1)无论哪种启动过程,机车的最大速度都等于其匀速运动时的速度,即vm=eq \f(P,Fmin)=eq \f(P,f)(式中Fmin为最小牵引力,其值等于阻力f).
(2)机车以恒定加速度启动的运动过程中,匀加速过程结束时,功率最大,速度不是最大,即v=eq \f(P,F)
【典例1】一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数(1/v)图象如图所示.若已知汽车的质量,则根据图象所给的信息,不能求出的物理量是( )
A.汽车的功率
B.汽车行驶的最大速度
C.汽车所受到的阻力
D.汽车运动到最大速度所需的时间
【典例2】在一段平直的公路上,质量为的汽车从静止开始做匀加速运动,经过一段时间,汽车速度达到。随后汽车以的额定功率沿平直公路继续前进,又经过达到最大速度,设汽车所受的阻力大小恒为。求:
(1)汽车行驶的最大速度的大小;
(2)汽车的速度为时的加速度大小;
分析机车启动问题时的注意事项
(1)机车启动的方式不同,机车运动的规律就不同,因此机车启动时,其功率、速度、加速度、牵引力等物理量的变化规律也不相同,分析图象时应注意坐标轴的意义及图象变化所描述的规律.
(2)恒定功率下的加速一定不是匀加速,这种加速过程发动机做的功可用W=Pt计算,不能用W=Fl计算(因为F是变力).
(3)以恒定牵引力加速时的功率一定不恒定,这种加速过程发动机做的功常用W=Fl计算,不能用W=Pt计算(因为功率P是变化的).
一、单选题
1.下列关于功的说法正确的是( )
A.做功的过程一定伴随着能量转化
B.功有正负之分,因此的功小于的功
C.根据功的定义式,可知功是既有大小又有方向的物理量
D.功就是能量,能量就是功,二者的含义是相同的
2.如图所示,质量为的物体静止在倾角为的斜面体上,现使斜面体水平向左匀速移动距离(物体与斜面体相对静止)。以下说法正确的是( )
A.摩擦力对物体做正功B.支持力对物体做功为0
C.支持力对物体做负功D.斜面体对物体做功为0
3.2023年1月5日,福建省重点工程漳州圆山大道项目全线通车。质量相等的甲、乙两车在运动时受到的阻力相等,时位于同一起始线,之后在平直公路上沿相邻车道同向运动,两车速度v随时间t变化的图像如图所示。下列说法正确的是( )
A.时两车功率相等
B.内两车牵引力始终不相等
C.乙追上甲前两车间的最大距离为
D.后乙车的功率始终大于甲车的
4.质量为的物体在水平面上沿直线运动,受阻力大小恒定。经某点开始沿运动方向的水平拉力F与运动距离x的关系如图所示,物体做匀速直线运动。下列对图示过程的说法正确的是( )
A.在处物体加速度大小为
B.阻力对物体做功为
C.拉力对物体做功为40J
D.合力对物体做功为
5.如图甲所示,物体受到水平推力F的作用在粗糙水平面上做直线运动。监测到推力F、物体速度v随时间t变化的规律如图乙、丙所示。取g=10m/s2,则( )
A.第1s内推力做功为2J
B.第2s内物体克服摩擦力做的功为4J
C.t=1.5s时推力F的瞬时功率为3W
D.第2s内推力F做功的平均功率为2W
6.野山鼠擅长打洞,假设山鼠打洞时受到的阻力与洞的深度成正比,即(为比例常数),则野山鼠打到洞深d的过程中,需要克服阻力做的功为( )
A.B.C.D.
7.如图1所示,静止于光滑水平面上坐标原点处的小物块,在水平拉力F作用下,沿x轴方向运动,拉力F的大小随物块所在位置坐标x的变化关系如图2所示,图线为半圆。则小物块运动到x0处时F所做的总功为( )
A.0B.Fmx0C.Fmx0D.
8.水平桌面上,长6m的轻绳一端固定于O点,如图所示(俯视图),另一端系一质量m=2.0kg的小球。现对小球施加一个沿桌面大小不变的力F=10N,F拉着物体从M点运动到N点,F的方向始终与小球的运动方向成37°角。已知小球与桌面间的动摩擦因数μ=0.2,不计空气阻力,取g=10m/s2,sin37°=0.6,cs37°=0.8,则下列说法正确的是( )
A.拉力F对小球做的功为16π(J)B.拉力F对小球做的功为8π(J)
C.小球克服摩擦力做的功为16π(J)D.小球克服摩擦力做的功为4π(J)
9.如图甲所示,一个倾角为的斜面固定在地面上,一辆质量为m的汽车由静止以额定功率P驶上斜面,汽车行驶的最大速度为v1;如图乙所示,若汽车从斜面顶端由静止以额定功率P向下运动,汽车行驶的最大速度为v2.已知汽车行驶过程中受到的阻力大小恒定不变,重力加速度为g,下列说法正确的是( )
A.汽车均做匀加速直线运动
B.最大行驶速度v1大于v2
C.阻力大小为
D.额定功率大小为
10.一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图像如图所示,已知汽车的质量,汽车受到地面的阻力为车重的0.1倍,()则( )
A.汽车在前5s内的牵引力为B.汽车的额定功率为90kW
C.汽车的最大速度为60m/s D.当汽车速度为30m/s时,汽车加速度大小为
11.一起重机的钢绳由静止开始匀加速提起质量为m的重物,当重物的速度为时,起重机的功率达到最大值P,之后起重机保持该功率不变,继续提升重物,最后重物以最大速度匀速上升,不计钢绳重力。则整个过程中,下列说法正确的是( )
A.钢绳的最大拉力为
B.重物匀加速过程的时间为
C.重物匀加速过程的加速度为
D.速度由增大至的过程中,重物的平均速度
12.全球最大水平臂上回转自升塔式起重机的开发和应用,意味着中国桥梁及铁路施工装备进一步迈向世界前列。该起重机某次从t=0时刻由静止开始提升质量为m的物体,其所受合外力随时间变化的图像如图所示,内起重机的功率为额定功率,不计物体受到的空气阻力,重力加速度为g,下列说法正确的是( )
A.物体匀加速阶段的加速度为
B.和时间内牵引力做的功之比为
C.时刻物体正在减速上升
D.阶段牵引力所做的功为
13.一台起重机将质量为m的重物竖直吊起(不计物体所受空气阻力),重力加速度为g,如图所示为该物体的速度—时间图像,其中时刻起重机输出功率达到最大,此后功率保持不变,最大速度为,由图可知( )
A.时间内,重物做匀加速运动且起重机输出功率恒定
B.起重机的最大输出功率为
C.时间内,起重机对重物做功为
D.时间内,起重机对重物做功为
二、多选题
14.电动汽车(BEV)是指以车载电源为动力,符合道路交通、安全法规各项要求的车辆。由于对环境影响相对传统汽车较小,其前景被广泛看好。某品牌纯电动车型部分参数:整备质量,驱动电机最大功率,该电动汽车在公路上行驶受到阻力大小恒为,则下列说法正确的是( )
A.汽车的最大速度为30m/s
B.汽车上坡时低速行驶,是为了使汽车获得较大的牵引力
C.汽车以的加速度匀加速启动时,牵引力为
D.里程过程中克服阻力所做的功约为
15.一个倾角为的斜面上有一个质量为m的小物块,随斜面一起以加速度匀加速下降一段高度h,则该过程中( )
A.斜面对小物块的摩擦力可能为零
B.斜面对小物块的弹力一定不为零
C.斜面对小物块做功为
D.斜面对小物块做功为
16.如图,在电梯中有一固定放置的倾角为θ的斜面,斜面上放置一个质量为m的物体,二者以相同的加速度a匀加速上升了高度h,且物体和斜面始终保持相对静止,在这一过程中,下列说法正确的是( )
A.斜面支持力对物体做的功为B.斜面对物体的摩擦力做的功为
C.斜面对物体做功为mahD.合力对物体做的功为mah
17.一质量为的物体在光滑的水平面上,在水平外力的作用下从静止开始做直线运动,外力的方向不变,大小随时间的变化关系如图所示。下列说法正确的是( )
A.时刻与时刻物体的速度大小之比为
B.与时间内物体的位移大小之比为
C.时刻外力对物体做功的瞬时功率为
D.时间内,外力对物体做功的平均功率为
18.汽车在研发过程中都要进行性能测试,如图所示为某次测试中某型号汽车的速度v与牵引力F大小倒数的图像,表示最大速度。已知汽车在水平路面上由静止启动,平行于v轴,反向延长过原点O。已知阻力恒定,汽车质量为,下列说法正确的是( )
A.汽车从a到b持续的时间为12.5s
B.汽车由b到c过程做匀加速直线运动
C.汽车额定功率为
D.汽车能够获得的最大速度为
三、解答题
19.如图所示,上表面段粗糙、段光滑,下表面粗糙的木板放置于水平地面上,可视为质点的滑块置于木板右端。时刻,分别给滑块、木板水平向左、向右的初速度v,一段时间后木板、滑块先后停止运动,整个过程中滑块始终在木板上。已知木板的质量,滑块的质量,滑块与木板上表面段的动摩擦因数,木板下表面与地面间的动摩擦因数,木板段长度,初速度大小,取重力加速度。不计空气阻力。求:
(1)运动过程中木板、滑块克服摩擦力所做的总功为多少?
(2)运动过程中木板克服滑块、地面的摩擦力所做的功分别为多少?
20.某人利用如图所示的装置,用100 N的恒力F作用于不计质量的细绳的一端,将物体从水平面上的A点移到B点。已知α1=30°,α2=37°,h=1.5 m,不计滑轮质量及绳与滑轮间的摩擦。求绳的拉力对物体所做的功(sin 37°=0.6,cs 37°=0.8)。
21.一辆汽车的额定功率为80kW,运动中所受的阻力恒为,汽车质量为,沿水平路面行驶,汽车运动过程中始终未超过额定功率。求:
(1)汽车行驶的最大速度;
(2)汽车以额定功率行驶,当车速为时汽车的加速度;
(3)若汽车以的加速度匀加速启动,当达到额定功率后以额定功率行驶。则启动1min的时间内汽车牵引力做的功(此时汽车以最大速度匀速行驶)。
适用条件
公式仅适用于求恒力做的功
影响因素
恒力做功大小只与F、l、α这三个量有关。与物体是否还受其他力、物体运动的速度和加速度等其他因素无关,也与物体运动的路径无关
各量的理解
力与位移以及它们间夹角的余弦的乘积(W=F·l·cs α)
力与在其方向上的分位移乘积(W=F·l cs α)
力在位移方向上的分力与位移的乘积(W=Fcs α·l)
区别与联系
平均功率
瞬时功率
区别
公式
或(F为恒力,为平均速度,α为F与之间的夹角)
(v为瞬时速度,α为F与v之间的夹角)
物理意义
表示力在一段时间内做功的平均快慢程度
表示力在一段极短时间内做功的快慢程度
对应关系
与某一段时间(或过程)相关,计算时应明确是哪个力在哪段时间(或过程)内做功的功率
与某一时刻(或状态)相关,计算时应明确是哪个力在哪个时刻(或状态)做功的功率
联系
在中.当t趋近于0时,所求的功率可视为瞬时功率
比较项目
定义
特点
联系
额定功率
发动机正常条件下长时间工作时的最大输出功率
不同机械额定功率可能不同,但同一机械额定功率不变
为了机械的安全
P额≥P实
实际功率
发动机实际工作时的输出功率
同一机械实际功率随工作情况的变化而改变
力与位移的夹角
在推力F作用下,斜面与物块一起水平运动
(1)G对m不做功
(2)FN对m做正功
(3)Ff对m做负功
力与瞬时速度的夹角
卫星由位置1到2的过程中,F与v的夹角大于90°做负功
两种模型
以恒定功率启动
以恒定加速度启动
P-t图和v-t图
OA段
过程分析
v↑⇒F=eq \f(P不变,v)↓⇒a=eq \f(F-f,m)↓
a=eq \f(F-F阻,m)不变⇒F不变eq \(⇒,\s\up6(v↑))P=Fv↑直到P额=Fv1
运动性质
加速度减小的加速直线运动
匀加速直线运动,维持时间t0=eq \f(v1,a)
AB
段
过程分析
F=f⇒a=0
⇒f=eq \f(P,vm)
v↑⇒F=eq \f(P额,v)↓
⇒a=eq \f(F-f,m)↓
运动性质
以vm做匀速直线运动
加速度减小的加速运动
BC段
无
F=f⇒a⇒0⇒
以vm=eq \f(P额, f)匀速运动
第5讲 功和功率
——划重点之精细讲义系列
知识1:功
1.做功的两个要素
力和物体在力的方向上发生的位移.
2.公式:W=Flcs α
(1)该公式只适用于恒力做功.
(2)α是力与位移方向的夹角,l为物体对地的位移.
3.功的正负的意义
(1)功是标量,但有正负之分,正功表示动力对物体做功,负功表示阻力对物体做功.
(2)一个力对物体做负功,往往说成是物体克服这个力做功(取绝对值).
知识2:功率
1.定义
功与完成这些功所用时间的比值.
2.物理意义
描述做功的快慢.
3.公式
(1)P=eq \f(W,t),P为时间t内的平均功率.
(2)P=Fvcs α(α为F与v的夹角)
①v为平均速度,则P为平均功率.
②v为瞬时速度,则P为瞬时功率.
4.额定功率与实际功率
【典例1】(多选)如图所示,在皮带传送装置中,皮带把物体P匀速带至高处,在此过程中,下述说法正确的是( )
A.摩擦力对物体做正功
B.摩擦力对物体做负功
C.支持力对物体不做功
D.合外力对物体做正功
【解析】 物体P匀速向上运动过程中,受静摩擦力作用,方向沿皮带向上,对物体做正功,支持力垂直于皮带,做功为零,合外力为零,做功也为零,故A、C正确,B、D错误.
【答案】 AC
【典例2】一人乘电梯从1楼到20楼,在此过程中经历了先加速,后匀速,再减速的运动过程,则电梯支持力对人做功情况是( )
A.加速时做正功,匀速时不做功,减速时做负功
B.加速时做正功,匀速和减速时做负功
C.加速和匀速时做正功,减速时做负功
D.始终做正功
【解析】 考查功的概念.人乘电梯时,无论是加速还是减速、匀速,支持力的方向总是向上,与运动方向相同,所以支持力与位移方向夹角小于90°,总是做正功,选D.
【答案】 D
【典例3】相同的恒力按同样方式施于静止的物体上,使它分别沿着粗糙水平地面和光滑水平地面移动相同的位移,恒力对物体做的功和平均功率分别为W1、P1和W2、P2则( )
A.W1>W2 P1>P2 B.W1=W2 P1
【典例4】为了响应国家的“节能减排”号召,某同学采用了一个家用汽车的节能方法.在符合安全行驶要求的情况下,通过减少汽车后备厢中放置的不常用物品和控制加油量等措施,使汽车负载减少.假设汽车以72 km/h的速度匀速行驶时,负载改变前、后汽车受到的阻力分别为2 000 N和1 950 N,请计算该方法使汽车发动机输出功率减少了多少?
【解析】 v=72 km/h=20 m/s,由P=Fv得
P1=F1v=Ff1v,P2=F2v=Ff2v,
故ΔP=P1-P2=(Ff1-Ff2)v=1×103 W.
【答案】 1×103 W
考点1:功的正负判断方法
1.根据夹角判断
2.从能的转化角度来进行判断
此法常用于判断相互联系的两个物体之间的相互作用力做功的情况.
例如,车M静止在光滑水平轨道上,球m用细线悬挂在车上,由中的位置无初速地释放,则可判断在球下摆过程中绳的拉力对车做正功.因为绳的拉力使车的动能增加了.又因为M和m构成的系统的机械能是守恒的,M增加的机械能等于m减少的机械能,所以绳的拉力一定对球m做负功.
【典例1】人造地球卫星在椭圆轨道上运行,由中的a点运动到b点的过程中( )
A.万有引力对卫星做正功
B.万有引力对卫星做负功
C.万有引力对卫星先做正功,再做负功
D.万有引力对卫星一直不做功
【解析】 由于图中万有引力与速度方向夹角始终小于90°,故在此过程中万有引力对卫星做正功,A正确.
【答案】 A
【典例2】(多选)如图所示,重球m用一条不可伸长的轻质细线拴住后悬于O点,重球置于一个斜面不光滑的斜劈M上,用水平力F向左推动斜劈M在光滑水平桌面上由位置甲匀速向左移动到位置乙,在此过程中,正确的说法是( )
A.M、m间的摩擦力对m不做功
B.M、m间的摩擦力对m做负功
C.F对M所做的功与m对M所做的功的绝对值相等
D.M、m间的弹力对m做正功
【审题指导】 审题时注意该题中的几个关键条件:
(1)斜面不光滑.
(2)光滑水平桌面.
(3)匀速.
【解析】 小球在向左摆动过程中,M对m的摩擦力方向与小球m的位移方向间夹角小于90°,故摩擦力对m做正功,A、B均错误;因M匀速向左运动,地面对M的支持力和M的重力不做功,一定有F对M所做的功与m对M所做的功合功为零,C正确;M对m的弹力方向与m位移方向夹角小于90°,故对m做正功,D项正确.
【答案】 CD
1.作用力与反作用力做功特点
作用力和反作用力虽然等大反向,但由于其分别作用在两个物体上,产生的位移效果无必然联系,故作用力和反作用力的功不一定一正一负,大小也不一定相等.
2.静摩擦力做功的特点
(1)静摩擦力可以做正功,也可以做负功,还可以不做功。
(2)在静摩擦力做功的过程中,静摩擦力起着传递机械能的作用,没有机械能转化为其他形式的能。
(3)相互摩擦的系统内,一对静摩擦力做功的代数和总为零。
3.滑动摩擦力做功的特点
(1)滑动摩擦力可以做正功,也可以做负功,还可以不做功。
(2)在一对滑动摩擦力做功的过程中,能量的转化有两个方面:一是相互摩擦的物体之间机械能的转移;二是机械能转化为内能,转化为内能的数值等于滑动摩擦力与相对路程的乘积。
(3)滑动摩擦力、空气阻力等做的功,在曲线运动或往返运动中等于力和路程(不是位移)的乘积。
考点2:功的计算
1.恒力做的功:直接用W=Flcs α计算.
2.合外力做的功
方法一:先求合外力F合,再用W合=F合lcs α求功.
方法二:先求各个力做的功W1、W2、W2、……,再应用W合=W1+W2+W3+……求合外力做的功.
3.变力做的功——将变力做功转化为恒力做功
(1)平均值法
当力的方向不变,大小随位移按线性规律变化时,可先求出力对位移的平均值,再由计算功,如弹簧弹力做的功。
(2)分段法
力在全程是变力,但在每一个阶段是恒力,这样就可以先计算每个阶段的功,再利用求和的方法计算整个过程中变力做的功。
(3)微元法
将运动过程无限分割,每一小段就可看成恒力做功,然后把各小段恒力做的功求出来,再求出代数和,即为全过程该变力所做的功。这种处理问题的方法具有普遍的适用性。但在高中阶段该方法主要用于处理大小不变、方向与运动方向始终相同或相反的变力做功的问题。如滑动摩擦力、空气阻力做功就属于这种类型。不难得出,这种情况下,力对物体做功的绝对值等于力与物体运动路程的乘积。
(4)转换研究对象法
如图所示,人站在地上以恒力拉绳子,使小车向左运动,求绳子拉力对小车所做的功。绳子拉力对小车来说是个变力(大小不变,方向改变),但仔细研究,发现人拉绳的力却是恒力,于是转换研究对象,用人拉绳的力所做的功来求绳子拉力对小车做的功。
2.图像法
如果参与做功的变力方向与位移方向始终共线而大小随位移变化,我们可作出该力随位移变化的图像,如图所示,这时变力做的功 W可用 F-l图线与l轴所围成的图形的面积来表示。l轴上方的面积表示力对物体做的正功的多少,l轴下方的面积表示力对物体做的负功的多少。
【典例1】如图所示,建筑工人通过滑轮装置将一质量是100 kg的料车沿30°角的斜面由底端匀速地拉到顶端,斜面长L是4 m,若不计滑轮的质量和各处的摩擦力,g取10 N/kg,求这一过程中
(1)人拉绳子的力做的功;
(2)物体的重力做的功;
(3)物体受到的合力对物体做的总功.
【解析】 (1)工人拉绳子的力:
F=eq \f(1,2)mgsin θ
工人将料车拉到斜面顶端时,拉绳子的长度:l=2L,根据公式W=Flcs α,得
W1=eq \f(1,2)mgsin θ·2L=2 000 J.
(2)重力做功:
W2=-mgh=-mgLsin θ=-2 000 J.
(3)由于料车在斜面上匀速运动,则料车所受的合力为0,故W合=0.
【答案】 (1)2 000 J (2)-2 000 J (3)0
【典例2】人在A点拉着绳通过一定滑轮吊起质量m=50 kg的物体,如图所示,开始时绳与水平方向的夹角为60°.当人匀速提起重物由A点沿水平方向运动l=2 m而到达B点时,绳与水平方向成30°角.则人对绳的拉力做了多少功?
【审题指导】 解答该题应注意:
(1)人对绳的拉力方向时刻变化,该力一定是变力.
(2)求变力的功要注意应用转化的思想,求人拉绳的功可转化为绳对物体拉力的功.
【解析】 人对绳的拉力的功与绳对物体的拉力的功是相同的,而由于匀速提升物体,故物体处于平衡状态,可知绳上拉力F=mg.而重物上升的高度h等于右侧绳子的伸长量Δl,由几何关系易得:h(ct 30°-ct 60°)=l,Δl=eq \f(h,sin 30°)-eq \f(h,sin 60°),解得Δl=1.46 m.人对绳子做的功W=mgΔl=500×1.46 J=730 J.
【答案】 730 J
公式W=Flcs α中位移“l”的意义:
(1)力对平动的物体(可看作质点)做功,“l”为物体上每一点的位移(即受力质点对地的位移).
(2)若受力物体发生转动或形变,“l”应取作用点的位移.
(3)“l”的取值一般以大地为参考系.
考点3:功率的计算
1.平均功率的计算方法
(1)利用eq \x\t(P)=eq \f(W,t).
(2)利用eq \x\t(P)=F·eq \x\t(v)cs θ,其中eq \x\t(v)为物体运动的平均速度,F为恒力.
2.瞬时功率的计算方法
(1)利用公式P=F·vcs θ,其中v为t时刻的瞬时速度.
(2)利用公式P=F·vF,其中vF为物体的速度v在力F方向上的分速度.
(3)利用公式P=Fv·v,其中Fv为物体受的外力F在速度v方向上的分力.
【典例1】如图所示,细线的一端固定于O点,另一端系一小球.在水平拉力作用下,小球以恒定速率在竖直平面内由A点运动到B点.在此过程中拉力的瞬时功率变化情况是( )
A.逐渐增大 B.逐渐减小
C.先增大,后减小 D.先减小,后增大
【解析】 小球速率恒定,由动能定理知:拉力做的功与克服重力做的功始终相等,将小球的速度分解,可发现小球在竖直方向分速度逐渐增大,重力的瞬时功率也逐渐增大,则拉力的瞬时功率也逐渐增大,A项正确.
【答案】 A
【典例2】如图甲所示,滑轮质量、摩擦均不计,质量为2 kg的物体在F作用下由静止开始向上做匀加速运动,其速度随时间的变化关系如图乙所示,g取10 m/s2.
求:(1)4 s末力F的瞬时功率;
(2)4 s内F做功的平均功率.
【审题指导】 根据物体的运动情况求出物体的加速度,由牛顿第二定律求出拉力F的大小,再由功和功率的公式进行计算.
【解析】 (1)由图象可得,物体的加速度
a=eq \f(2,4) m/s2=0.5 m/s2
由牛顿第二定律2F-mg=ma,
解得F=10.5 N
4 s末F的瞬时功率为:
P=Fv=10.5×2×2 W=42 W.
(2)4 s内的平均功率
eq \x\t(P) =Feq \x\t(v) =10.5×2 W=21 W.
【答案】 (1)42 W (2)21 W
求力做功的功率时应注意的问题
(1)首先要明确所求功率是平均功率还是瞬时功率,对应于某一过程的功率为平均功率,对应于某一时刻的功率为瞬时功率.
(2)求功率大小时要注意F与v方向间的夹角α对结果的影响.
(3)用P=F·eq \x\t(v)cs α求平均功率时,eq \x\t(v)应容易求得,如求匀变速直线运动中某力的平均功率.
机车的两种启动模型的分析
1.模型综述
物体在牵引力(受功率和速度制约)作用下,从静止开始克服一定的阻力,加速度不变或变化,最终加速度等于零,速度达到最大值.
2.两种模型的比较
(1)两种启动方式的比较
(2)三个重要关系式
(1)无论哪种启动过程,机车的最大速度都等于其匀速运动时的速度,即vm=eq \f(P,Fmin)=eq \f(P,f)(式中Fmin为最小牵引力,其值等于阻力f).
(2)机车以恒定加速度启动的运动过程中,匀加速过程结束时,功率最大,速度不是最大,即v=eq \f(P,F)
【典例1】一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数(1/v)图象如图所示.若已知汽车的质量,则根据图象所给的信息,不能求出的物理量是( )
A.汽车的功率
B.汽车行驶的最大速度
C.汽车所受到的阻力
D.汽车运动到最大速度所需的时间
【解析】 由P=F·v和F-Ff=ma得出:a=eq \f(P,m)·eq \f(1,v)-eq \f(Ff,m),由图象可求出图线斜率k,则k=eq \f(P,m),可求出汽车的功率P,由eq \f(1,v)=0时,a=-2 m/s2,得:-2=-eq \f(Ff,m)可求出汽车所受阻力Ff,再由P=Ff·vm可求出汽车运动的最大速度vm,但汽车做变加速直线运动,无法求出汽车运动到最大速度的时间,故选D.
【答案】 D
【典例2】在一段平直的公路上,质量为的汽车从静止开始做匀加速运动,经过一段时间,汽车速度达到。随后汽车以的额定功率沿平直公路继续前进,又经过达到最大速度,设汽车所受的阻力大小恒为。求:
(1)汽车行驶的最大速度的大小;
(2)汽车的速度为时的加速度大小;
【答案】(1);(2)
【详解】(1)根据题意可知,汽车速度最大时,加速度为0,即牵引力等于阻力,设最大速度为,则有
解得
(2)根据题意,由公式可得,汽车的速度为时,牵引力为
由牛顿第二定律有
解得
分析机车启动问题时的注意事项
(1)机车启动的方式不同,机车运动的规律就不同,因此机车启动时,其功率、速度、加速度、牵引力等物理量的变化规律也不相同,分析图象时应注意坐标轴的意义及图象变化所描述的规律.
(2)恒定功率下的加速一定不是匀加速,这种加速过程发动机做的功可用W=Pt计算,不能用W=Fl计算(因为F是变力).
(3)以恒定牵引力加速时的功率一定不恒定,这种加速过程发动机做的功常用W=Fl计算,不能用W=Pt计算(因为功率P是变化的).
一、单选题
1.下列关于功的说法正确的是( )
A.做功的过程一定伴随着能量转化
B.功有正负之分,因此的功小于的功
C.根据功的定义式,可知功是既有大小又有方向的物理量
D.功就是能量,能量就是功,二者的含义是相同的
【答案】A
【详解】AD.功与能是两个不同的物理量,功是能量转化的量度,做多少功,就有多少能量转化,所以做功的的过程一定伴随着能量转化,故A正确,D错误;
B.功有正负之分,力做负功表示物体克服该力做功,但做功的多少比较的是绝对值,因此的功大于的功,故B错误;
C.功是标量,只有大小没有方向,故C错误;
故选A。
2.如图所示,质量为的物体静止在倾角为的斜面体上,现使斜面体水平向左匀速移动距离(物体与斜面体相对静止)。以下说法正确的是( )
A.摩擦力对物体做正功B.支持力对物体做功为0
C.支持力对物体做负功D.斜面体对物体做功为0
【答案】D
【详解】根据题意,对物体受力分析,如图所示
由平衡条件有
由做功公式可得,支持力对物体做功为
可知,支持力做正功,摩擦力做功为
可知,摩擦力做负功,则斜面体对物体做功为
故选D。
3.2023年1月5日,福建省重点工程漳州圆山大道项目全线通车。质量相等的甲、乙两车在运动时受到的阻力相等,时位于同一起始线,之后在平直公路上沿相邻车道同向运动,两车速度v随时间t变化的图像如图所示。下列说法正确的是( )
A.时两车功率相等
B.内两车牵引力始终不相等
C.乙追上甲前两车间的最大距离为
D.后乙车的功率始终大于甲车的
【答案】B
【详解】A.由图可知,时两车速度相等,甲车达到最大速度,牵引力等于阻力,乙车做加速运动,牵引力大于阻力,则两车功率不相等,故A错误;
B.由图可知,内,甲车做匀速直线运动,牵引力等于阻力,乙车做加速运动,牵引力大于阻力,则内两车牵引力始终不相等,故B正确;
C.根据题意可知,速度相等时两车间的距离最大,由图像面积可知,最大距离为
故C错误;
D.根据题意可知,后甲车的功率不变,乙车的功率从零开始增大,开始一段时间内乙的功率小于甲车的功率,故D错误。
故选B。
4.质量为的物体在水平面上沿直线运动,受阻力大小恒定。经某点开始沿运动方向的水平拉力F与运动距离x的关系如图所示,物体做匀速直线运动。下列对图示过程的说法正确的是( )
A.在处物体加速度大小为
B.阻力对物体做功为
C.拉力对物体做功为40J
D.合力对物体做功为
【答案】C
【详解】A.由于在物体做匀速直线运动,拉力与阻力大小相等,因此物体所受的阻力大小为
由图像可知,在处物体,物体所受的拉力为7N,根据牛顿第二定律
可知在该位置的加速度
A错误;
B.阻力对物体做功
B错误;
C.根据图像可知,拉力最物体做的功等于图像与横轴围成的面积,即
C正确;
D.合力对物体做的功
D错误。
故选C。
5.如图甲所示,物体受到水平推力F的作用在粗糙水平面上做直线运动。监测到推力F、物体速度v随时间t变化的规律如图乙、丙所示。取g=10m/s2,则( )
A.第1s内推力做功为2J
B.第2s内物体克服摩擦力做的功为4J
C.t=1.5s时推力F的瞬时功率为3W
D.第2s内推力F做功的平均功率为2W
【答案】C
【详解】A.第1s内推力方向上没有位移,所以不做功,故A错误。
B.根据图像,第2s内位移为
摩擦力方向向左
摩擦力做负功
所以第2s内物体克服摩擦力做的功为2J,故B错误;
C.根据图像可知,1.5s时,物体的速度为
推力
F=3N
推力F在第1.5s时的功率
故C正确;
D.根据图像,第2s内的平均速度为
推力
F=3N
所以第2s内推力F做功的平均功率
故D错误。
故选C。
6.野山鼠擅长打洞,假设山鼠打洞时受到的阻力与洞的深度成正比,即(为比例常数),则野山鼠打到洞深d的过程中,需要克服阻力做的功为( )
A.B.C.D.
【答案】B
【详解】由于山鼠打洞时受到的阻力与洞的深度成正比,则野山鼠打到洞深d的过程中,需要克服阻力做的功为
故选B。
7.如图1所示,静止于光滑水平面上坐标原点处的小物块,在水平拉力F作用下,沿x轴方向运动,拉力F的大小随物块所在位置坐标x的变化关系如图2所示,图线为半圆。则小物块运动到x0处时F所做的总功为( )
A.0B.Fmx0C.Fmx0D.
【答案】C
【详解】在F-x图像中,图线与x轴所围面积的代数和就表示力F在这段位移内所做的功,面积
W=S===Fm·=Fmx0=
故选C。
8.水平桌面上,长6m的轻绳一端固定于O点,如图所示(俯视图),另一端系一质量m=2.0kg的小球。现对小球施加一个沿桌面大小不变的力F=10N,F拉着物体从M点运动到N点,F的方向始终与小球的运动方向成37°角。已知小球与桌面间的动摩擦因数μ=0.2,不计空气阻力,取g=10m/s2,sin37°=0.6,cs37°=0.8,则下列说法正确的是( )
A.拉力F对小球做的功为16π(J)B.拉力F对小球做的功为8π(J)
C.小球克服摩擦力做的功为16π(J)D.小球克服摩擦力做的功为4π(J)
【答案】A
【详解】AB.将圆弧分成很多小段l1,l2,…,ln,拉力F在每小段上做的功为W1,W2,…,Wn,因拉力F大小不变,方向始终与小球的运动方向成37°角,所以
W1=Fl1cs37°
W2=Fl2cs37°
Wn=Flncs37°
故
故A正确,B错误;
CD.同理可得小球克服摩擦力做的功
故CD错误。
故选A。
9.如图甲所示,一个倾角为的斜面固定在地面上,一辆质量为m的汽车由静止以额定功率P驶上斜面,汽车行驶的最大速度为v1;如图乙所示,若汽车从斜面顶端由静止以额定功率P向下运动,汽车行驶的最大速度为v2.已知汽车行驶过程中受到的阻力大小恒定不变,重力加速度为g,下列说法正确的是( )
A.汽车均做匀加速直线运动
B.最大行驶速度v1大于v2
C.阻力大小为
D.额定功率大小为
【答案】D
【详解】A.汽车以额定功率行驶,做加速度减小的加速运动,当加速度减为零时,速度达到最大,因此汽车均做变加速直线运动,A错误;
BCD.设汽车行驶过程中受到的阻力为,当汽车达到最大速度时,加速度为零,对题图甲有,牵引力
额定功率
对题图乙有,牵引力
额定功率
联立可得
,
故
D正确,BC错误。
故选D。
10.一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图像如图所示,已知汽车的质量,汽车受到地面的阻力为车重的0.1倍,()则( )
A.汽车在前5s内的牵引力为B.汽车的额定功率为90kW
C.汽车的最大速度为60m/sD.当汽车速度为30m/s时,汽车加速度大小为
【答案】C
【详解】A.由图像可知,匀加速过程中的加速度
根据牛顿第二定律
可知在该过程中的牵引力
A错误;
B.汽车的额定功率
B错误;
C.当牵引力等于阻力时,速度最大,则最大速度
C正确;
D.当汽车速度为30m/s时,牵引力
此时的加速度
D错误。
故选C。
11.一起重机的钢绳由静止开始匀加速提起质量为m的重物,当重物的速度为时,起重机的功率达到最大值P,之后起重机保持该功率不变,继续提升重物,最后重物以最大速度匀速上升,不计钢绳重力。则整个过程中,下列说法正确的是( )
A.钢绳的最大拉力为
B.重物匀加速过程的时间为
C.重物匀加速过程的加速度为
D.速度由增大至的过程中,重物的平均速度
【答案】B
【详解】A.在匀加速过程,钢绳拉力F恒定,功率随速度正比增大,由得匀加速运动阶段钢绳的拉力为
故A错误;
BC.重物匀加速过程,根据牛顿第二定律可得
又
,
联立解得
,
故B正确,C错误;
D.在速度由增大至的过程中,功率P恒定,由可知随速度增大,钢绳拉力在减小,根据
可知a减小,即重物做加速度减小的变加速运动,则平均速度满足
故D错误。
故选B。
12.全球最大水平臂上回转自升塔式起重机的开发和应用,意味着中国桥梁及铁路施工装备进一步迈向世界前列。该起重机某次从t=0时刻由静止开始提升质量为m的物体,其所受合外力随时间变化的图像如图所示,内起重机的功率为额定功率,不计物体受到的空气阻力,重力加速度为g,下列说法正确的是( )
A.物体匀加速阶段的加速度为
B.和时间内牵引力做的功之比为
C.时刻物体正在减速上升
D.阶段牵引力所做的功为
【答案】B
【详解】A.题图纵轴表示合外力,因此时间内,物体加速度为
故A错误;
BD.时间内牵引力做功为
时间内牵引力做功为
联立可得和时间内牵引力做的功之比为
故B正确,D错误;
C.由题图可知时刻合外力仍大于零,合外力仍向上,物体继续做加速运动,故C错误。
故选B。
13.一台起重机将质量为m的重物竖直吊起(不计物体所受空气阻力),重力加速度为g,如图所示为该物体的速度—时间图像,其中时刻起重机输出功率达到最大,此后功率保持不变,最大速度为,由图可知( )
A.时间内,重物做匀加速运动且起重机输出功率恒定
B.起重机的最大输出功率为
C.时间内,起重机对重物做功为
D.时间内,起重机对重物做功为
【答案】B
【详解】A.速度—时间图像的斜率表示加速度,可知,时间内,重物做匀加速运动,牵引力一定,根据
可知,当牵引力一定时,速度增大,起重机输出功率增大,A错误;
B.根据图像可知,时刻之后,重物做匀速直线运动,则有
,
解得起重机的最大输出功率为
B正确;
D.时间内,重物上升的位移为
起重机对重物做功为W1,则有
解得
D错误;
C.时间内,令该段时间上升的高度为h,根据动能定理有
解得
C错误。
故选B。
二、多选题
14.电动汽车(BEV)是指以车载电源为动力,符合道路交通、安全法规各项要求的车辆。由于对环境影响相对传统汽车较小,其前景被广泛看好。某品牌纯电动车型部分参数:整备质量,驱动电机最大功率,该电动汽车在公路上行驶受到阻力大小恒为,则下列说法正确的是( )
A.汽车的最大速度为30m/s
B.汽车上坡时低速行驶,是为了使汽车获得较大的牵引力
C.汽车以的加速度匀加速启动时,牵引力为
D.里程过程中克服阻力所做的功约为
【答案】AB
【详解】A.当汽车以最大速度行驶时,其牵引力与阻力大小相等,则
代入解得,汽车的最大速度为
A正确;
B.根据可知,功率保持不变,汽车上坡时低速行驶,是为了使汽车获得较大的牵引力,B正确;
C.汽车以的加速度匀加速启动时,由牛顿第二定律
可得,牵引力大小为
C错误;
D.里程过程中克服阻力所做的功为
D错误。
故选AB。
15.一个倾角为的斜面上有一个质量为m的小物块,随斜面一起以加速度匀加速下降一段高度h,则该过程中( )
A.斜面对小物块的摩擦力可能为零
B.斜面对小物块的弹力一定不为零
C.斜面对小物块做功为
D.斜面对小物块做功为
【答案】BD
【详解】AB.对小物块受力分析如图所示
在水平方向
在竖直方向,根据牛顿第二定律
解得
因为,所以斜面对小物块的摩擦力不可能为零,斜面对小物块的弹力一定不为零,故B正确,A错误;
CD.斜面对木块的合力为
所以斜面对小物块做功为
故C错误,D正确。
故选BD。
16.如图,在电梯中有一固定放置的倾角为θ的斜面,斜面上放置一个质量为m的物体,二者以相同的加速度a匀加速上升了高度h,且物体和斜面始终保持相对静止,在这一过程中,下列说法正确的是( )
A.斜面支持力对物体做的功为B.斜面对物体的摩擦力做的功为
C.斜面对物体做功为mahD.合力对物体做的功为mah
【答案】AD
【详解】AB.对m受力分析如图
水平和竖直方向分别由动力学方程
解得
根据定义分别计算出二者的做功
故A正确,B错误;
CD.斜面对物体有2个力,所以做功为二者之和
合力做功由斜面对物体做的正功和重力做的负功两部分之和
再根据牛顿第二定律
同样可得
故C错误,D正确。
故选AD。
17.一质量为的物体在光滑的水平面上,在水平外力的作用下从静止开始做直线运动,外力的方向不变,大小随时间的变化关系如图所示。下列说法正确的是( )
A.时刻与时刻物体的速度大小之比为
B.与时间内物体的位移大小之比为
C.时刻外力对物体做功的瞬时功率为
D.时间内,外力对物体做功的平均功率为
【答案】BCD
【详解】AB.内物体的加速度为
时刻物体的速度大小为
时刻物体的速度大小为
内物体的位移大小为
内物体的加速度为
时刻物体的速度大小为
内物体的位移大小为
则时刻与时刻物体的速度大小之比为
与时间内物体的位移大小之比为
故A错误,B正确;
C.时刻外力对物体做功的瞬时功率为
故C正确;
D.时间内,外力对物体做的功为
时间内,外力F对物体做功的平均功率为
故D正确。
故选BCD。
18.汽车在研发过程中都要进行性能测试,如图所示为某次测试中某型号汽车的速度v与牵引力F大小倒数的图像,表示最大速度。已知汽车在水平路面上由静止启动,平行于v轴,反向延长过原点O。已知阻力恒定,汽车质量为,下列说法正确的是( )
A.汽车从a到b持续的时间为12.5s
B.汽车由b到c过程做匀加速直线运动
C.汽车额定功率为
D.汽车能够获得的最大速度为
【答案】AC
【详解】C.根据 ,额定功率等于图线的斜率
C正确;
B.根据 ,汽车由b到c过程功率不变,随着汽车速度的增大,牵引力减小;根据牛顿第二定律得
汽车所受阻力不变,随着牵引力的减小,汽车的加速度减小,汽车由b到c过程做非匀变速直线运动,B错误;
D.汽车能够获得的最大速度为
D错误;
A.汽车所受的阻力为
汽车从a到b所受的牵引力为
解得
根据牛顿第二定律得
解得
汽车从a到b持续的时间为
A正确。
故选AC。
三、解答题
19.如图所示,上表面段粗糙、段光滑,下表面粗糙的木板放置于水平地面上,可视为质点的滑块置于木板右端。时刻,分别给滑块、木板水平向左、向右的初速度v,一段时间后木板、滑块先后停止运动,整个过程中滑块始终在木板上。已知木板的质量,滑块的质量,滑块与木板上表面段的动摩擦因数,木板下表面与地面间的动摩擦因数,木板段长度,初速度大小,取重力加速度。不计空气阻力。求:
(1)运动过程中木板、滑块克服摩擦力所做的总功为多少?
(2)运动过程中木板克服滑块、地面的摩擦力所做的功分别为多少?
【答案】.(1)0.8J;(2),
【详解】(1)在滑块运动到C点前向,滑块做匀速运动,此时木板做匀减速运动的加速度大小为
设经过时间t滑块运动到C点,对该段时间有
即
同时对时间t应有
代入数值解得
此时木板的速度和运动的位移分别为
,
滑块运动到C点后,滑块和木板的加速度大小分别为
,
分析可知木板先停止,因为有
所以当木板停止后,滑块继续向左减速直到停止,而木板一直静止,故从滑块运动到C点到木板停止该段时间木板的位移为
从滑块运动到C点到滑块停止时,滑块的位移为
故运动过程中木板、滑块克服摩擦力所做的总功为
(2)根据前面分析可得运动过程中木板克服滑块摩擦力所做的功为
运动过程中木板克服地面的摩擦力所做的功为
20.某人利用如图所示的装置,用100 N的恒力F作用于不计质量的细绳的一端,将物体从水平面上的A点移到B点。已知α1=30°,α2=37°,h=1.5 m,不计滑轮质量及绳与滑轮间的摩擦。求绳的拉力对物体所做的功(sin 37°=0.6,cs 37°=0.8)。
【答案】50 J
【详解】由于不计绳的质量及绳与滑轮间的摩擦,故恒力F做的功和绳对物体的拉力做的功相等。由于恒力F作用在绳的端点,故需先求出绳的端点的位移l,再求恒力F做的功。
由几何关系知,绳的端点的位移为
l=-=h=0.5 m
在物体从A移到B的过程中,恒力F做的功为
W=Fl=100×0.5 J=50 J
故绳的拉力对物体所做的功为50 J。
21.一辆汽车的额定功率为80kW,运动中所受的阻力恒为,汽车质量为,沿水平路面行驶,汽车运动过程中始终未超过额定功率。求:
(1)汽车行驶的最大速度;
(2)汽车以额定功率行驶,当车速为时汽车的加速度;
(3)若汽车以的加速度匀加速启动,当达到额定功率后以额定功率行驶。则启动1min的时间内汽车牵引力做的功(此时汽车以最大速度匀速行驶)。
【答案】(1);(2);(3)
【详解】(1)当汽车的牵引力和阻力相等时,汽车达到最大速度,即
由
可得,汽车最大速度为
解得
(2)当车速为
由
P=Fv
可知,此时汽车的牵引力为
所以此时的加速度大小为
(3)当汽车以1m/s2的加速度匀加速启动时,由
可得此时的牵引力的大小为
由
可得,匀加速运动的最大速度为
匀加速运动的时间
所以启动1min的时间内汽车先匀加速运动10s,后50s内汽车的功率不变,在前10s内汽车的位移为
牵引力做功
在后50s内牵引力做功
故总功为
适用条件
公式仅适用于求恒力做的功
影响因素
恒力做功大小只与F、l、α这三个量有关。与物体是否还受其他力、物体运动的速度和加速度等其他因素无关,也与物体运动的路径无关
各量的理解
力与位移以及它们间夹角的余弦的乘积(W=F·l·cs α)
力与在其方向上的分位移乘积(W=F·l cs α)
力在位移方向上的分力与位移的乘积(W=Fcs α·l)
区别与联系
平均功率
瞬时功率
区别
公式
或(F为恒力,为平均速度,α为F与之间的夹角)
(v为瞬时速度,α为F与v之间的夹角)
物理意义
表示力在一段时间内做功的平均快慢程度
表示力在一段极短时间内做功的快慢程度
对应关系
与某一段时间(或过程)相关,计算时应明确是哪个力在哪段时间(或过程)内做功的功率
与某一时刻(或状态)相关,计算时应明确是哪个力在哪个时刻(或状态)做功的功率
联系
在中.当t趋近于0时,所求的功率可视为瞬时功率
比较项目
定义
特点
联系
额定功率
发动机正常条件下长时间工作时的最大输出功率
不同机械额定功率可能不同,但同一机械额定功率不变
为了机械的安全
P额≥P实
实际功率
发动机实际工作时的输出功率
同一机械实际功率随工作情况的变化而改变
力与位移的夹角
在推力F作用下,斜面与物块一起水平运动
(1)G对m不做功
(2)FN对m做正功
(3)Ff对m做负功
力与瞬时速度的夹角
卫星由位置1到2的过程中,F与v的夹角大于90°做负功
两种模型
以恒定功率启动
以恒定加速度启动
P-t图和v-t图
OA段
过程分析
v↑⇒F=eq \f(P不变,v)↓⇒a=eq \f(F-f,m)↓
a=eq \f(F-F阻,m)不变⇒F不变eq \(⇒,\s\up6(v↑))P=Fv↑直到P额=Fv1
运动性质
加速度减小的加速直线运动
匀加速直线运动,维持时间t0=eq \f(v1,a)
AB
段
过程分析
F=f⇒a=0
⇒f=eq \f(P,vm)
v↑⇒F=eq \f(P额,v)↓
⇒a=eq \f(F-f,m)↓
运动性质
以vm做匀速直线运动
加速度减小的加速运动
BC段
无
F=f⇒a⇒0⇒
以vm=eq \f(P额, f)匀速运动
高一物理下学期期末复习精细讲义(人教2019)第6讲动能定理(原卷版+解析): 这是一份高一物理下学期期末复习精细讲义(人教2019)第6讲动能定理(原卷版+解析),共46页。试卷主要包含了公式,矢标性,动能的变化量,适用条件等内容,欢迎下载使用。
高一物理下学期期末复习精细讲义(人教2019)第3讲 圆周运动(原卷版+解析): 这是一份高一物理下学期期末复习精细讲义(人教2019)第3讲 圆周运动(原卷版+解析),共52页。试卷主要包含了线速度,角速度,周期和频率,向心加速度,向心力,相互关系等内容,欢迎下载使用。
高一物理下学期期末复习精细讲义(人教2019)第1讲 曲线运动(原卷版+解析): 这是一份高一物理下学期期末复习精细讲义(人教2019)第1讲 曲线运动(原卷版+解析),共43页。试卷主要包含了速度的方向,运动的性质,曲线运动的条件,合运动与分运动的关系等内容,欢迎下载使用。












