

初中数学沪教版 (五四制)七年级上册9.4 整式达标测试
展开目录
TOC \ "1-3" \h \u \l "_Tc5998" 【典型例题】 PAGEREF _Tc5998 \h 1
\l "_Tc11367" 【考点一 整式乘法公式的辨析】 PAGEREF _Tc11367 \h 1
\l "_Tc11504" 【考点二 乘法公式在几何图形中的应用】2
\l "_Tc11577" 【考点三 利用乘法公式简便运算】3
\l "_Tc23605" 【考点四 乘法公式计算的拓展提高】3
\l "_Tc21571" 【过关检测】4
【典型例题】
【考点一 整式乘法公式的辨析】
【例题1】下列多项式相乘,不能用平方差公式计算的是( )
A.B.
C.D.
【变式1】如果是完全平方式,那么m的值为 .
【变式2】在下列多项式的乘法中,可以用平方差公式计算的是( )
A.B.
C. D.
【考点二 乘法公式在几何图形中的应用】
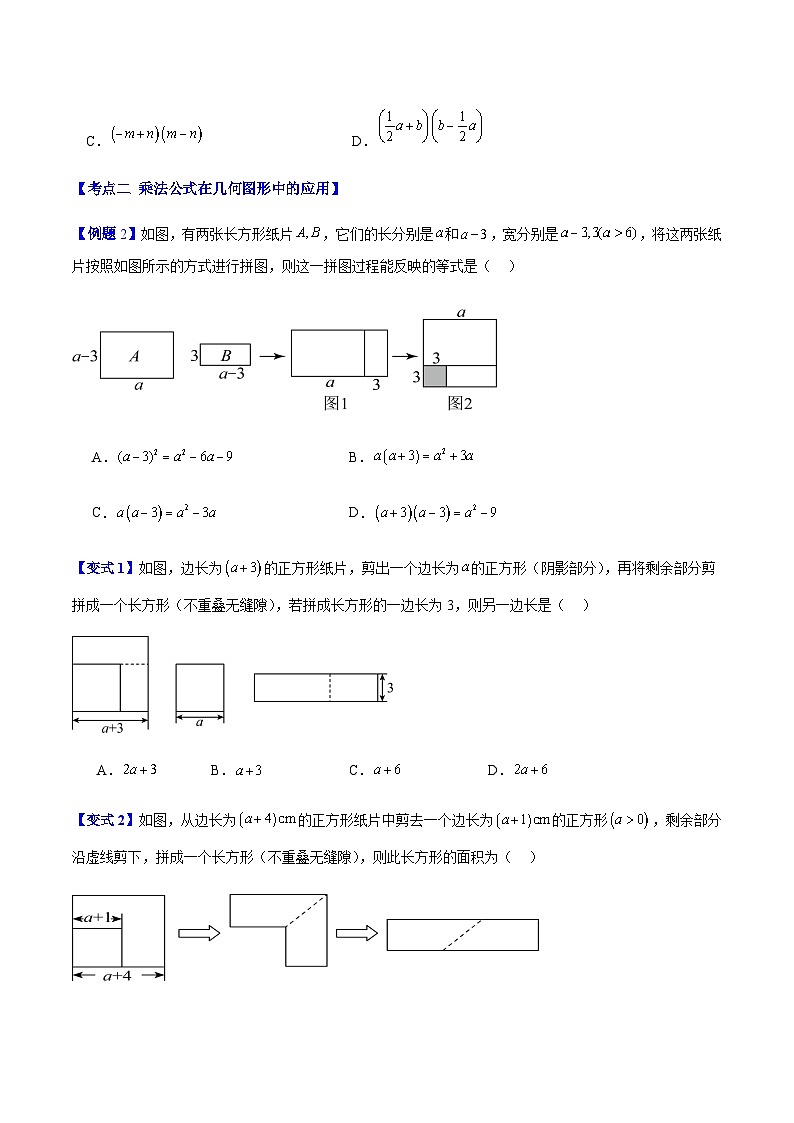
【例题2】如图,有两张长方形纸片,它们的长分别是和,宽分别是,将这两张纸片按照如图所示的方式进行拼图,则这一拼图过程能反映的等式是( )
A.B.
C.D.
【变式1】如图,边长为的正方形纸片,剪出一个边长为的正方形(阴影部分),再将剩余部分剪拼成一个长方形(不重叠无缝隙),若拼成长方形的一边长为3,则另一边长是( )
A.B.C.D.
【变式2】如图,从边长为的正方形纸片中剪去一个边长为的正方形,剩余部分沿虚线剪下,拼成一个长方形(不重叠无缝隙),则此长方形的面积为( )
A.B.
C.D.
【变式3】用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是169,小正方形的面积是9,若用x,y表示矩形的长和宽(),则下列关系式中不正确的是( )
A.B.C.D.
【考点三 利用乘法公式的简便运算】
【例题3】计算的结果是( )
A.B.0C.1D.
【变式1】如果有理数、同时满足,那么的值为( )
A.B.C.D.以上答案都不对
【变式2】21.计算的结果是( )
A.B.
C.D.
【变式3】式子化简的结果为( )
A.B.C.D.
【考点四 乘法公式的计算提高】
【例题4】小颖在计算时,把3写成后,发现可以连续运用平方差公式进行计算.计算:( )
A.B.C.D.
【变式1】如图,麦麦用9张A类正方形卡片、1张B类正方形卡片和6张C类长方形卡片,拼成了一个大正方形,拼成的大正方形的边长是( )
A.B.C.D.
【变式2】观察下列运算并填空:
;
;
;
…
根据以上结果,猜想: .
【过关检测】
一.选择题
1.下列各式中,能使用平方差公式计算的是( )
A.B.
C.D.
2.计算等于( )
A.B.C.D.
3.下列运算不能用平方差公式的是( )
A.B.
C.D.
4.如果,那么的值为( )
A.B.C.D.
5.若______,则横线上分别应填( )
A.、B.、C.、D.、
6. 如图,将四个长为a,宽为b的小长方形纸片拼成一个大正方形,用两种不同的方法表示这个大正方形的面积,则可以得出一个等式为( )
A.B.
C.D.
7.如图:把长和宽分别为a和 b的四个完全相同的小长方形(a>b)拼成的一个“回形”正方形,图中的阴影部分的面积正好可以验证下面等式的正确性的是( )
A.B.
C. D.
8.如图,根据标注该图所反映的乘法公式是( ).
A.B.
C.D.
9.图(1)是一个长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,小长方形的长为,宽为,然后按图(2)拼成一个正方形,通过计算,用拼接前后两个图形中阴影部分的面积可以验证的等式是( )
A.B.
C.D.
二. 填空题
10.在数学中,有时会出现大数值的运算.在学习了整式的乘法以后,通过用字母代替数转化成整式乘法来解决,能达到化繁为简的效果。例:若,,比较、的大小时,设,则,.∵,∴.参考上述解题过程,计算: .
三、解答题
11.图1、图2分别由两个长方形拼成.
(1)图1中图形的面积为 ,图2中图形的面积为( );(用含有a、b的代数式表示)
(2)由(1)可以得到等式: ;
(3)根据你得到的等式解决下列问题:
①计算:;
②若,求的值.
12.将边长为的正方形的左上角剪掉一个边长为的正方形如图,将剩下部分按照虚线分割成①和②两部分,将①和②两部分拼成一个长方形如图,解答下列问题:
(1)设图中阴影部分的面积为,图中阴影部分的面积为,请用含,的式子表示: ______ , ______ ;不必化简
(2)由(1)中的结果可以验证的乘法公式是______ ;
(3)利用(2)中得到的公式,计算:.
13.长为的正方形中剪掉一个边长为的正方形(如图),然后将剩余部分拼成一个长方形(如图)
(1)上述操作能验证的等式是___________(请选择正确的一个)
A.
B.
C.
(2)应用你从()选出的等式,完成下面习题:
①已知,,求的值;
②计算
14.如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示)
(1)【探究】通过观察比较图2与图1中的阴影部分面积,可以得到乘法公式_______;(用含a,b的等式表示)
(2)【应用】请应用这个公式完成下列各题:
①已知,则值为________;
②计算:;
15.如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿线剪开,如图所示,拼成图②的长方形.
(1)请你表示出图①中阴影部分的面积_________________________;
请你表示出图②中阴影部分的面积_________________________;
(2)比较两图的阴影部分面积,可以得到乘法公式:_________________________;
(3)请应用公式计算:.
16.如图,在边长为的正方形中挖去一个边长为的小正方形,把余下的部分剪拼成一个矩形.
(1)通过计算两个图形的面积阴影部分的面积,可以验证的等式是______ ;请选择正确的一个
A.
B.
C.
D.
(2)应用你从(1)选出的等式,完成下列各题:
①已知,,求的值.
②计算:
17.若干张长方形和正方形卡片如图所示.
(1)选取1张①号卡片、4张②号卡片、4张③号卡片,请你拼出一个正方形.给出理由并画出图形.
(2)若已选取2张①号卡片、1张②号卡片,则还需要几张③号卡片才能拼出一个长方形?给出理由并画出图形.
18.在学习“整式的乘除”这一章时,我们经常构造几何图形来对代数式的变形加以说明,借助直观,形象的几何模型加深对乘法公式的认识和理解.
阅读下列材料:
材料1:如图1,现有甲,乙,丙三种型号的卡片若干张,其中甲型号卡片是边长为的正方形,乙型号卡片边长为的正方形,丙型号卡片是长为宽为的长方形.
材料2:用张甲,张乙和张丙型号的卡片,拼成正方形,
可以验证:,
验证如下:从整体看是一个边长为的正方形,所以.
从正方形的分割情况看,它的面积是由张甲,张乙和张丙卡片的面积之和,所以,比较两种不同的计算方法,可得.
根据以上材料,解答以下问题
(1)用图中的卡片,拼成图所示长方形,可以验证的等式为: ;
(2)用张丙型号的卡片拼成图所示正方形框,中间的阴影部分是边长为 的正方形,现用两种不同的方法计算阴影部分的面积,可以验证的等式为: ;
(3)已知图中的纸片(足够多),利用种卡片设计一个几何图形来计算画出图形,写出验过程.
19.通常用两种不同的方法计算同一个图形的面积,可以得到一个恒等式,例如:如图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形,请解答下列问题:
(1)图②中阴影部分的正方形边长的是:______.
(2)用两种不同的方法求图②中阴影部分的面积:方法1:______;方法2:______.
(3)观察图②,请你写出.,之间的等量关系______;
(4)根据(3)中的等量关系解决如下问题:若,,则______.
初中数学沪教版 (五四制)七年级上册第九章 整式第1节 整式的概念9.4 整式课后测评: 这是一份初中数学沪教版 (五四制)七年级上册<a href="/sx/tb_c18630_t7/?tag_id=28" target="_blank">第九章 整式第1节 整式的概念9.4 整式课后测评</a>,共6页。
专题02 整式与因式分解(18题型+真题过关)(解析版+原卷版): 这是一份专题02 整式与因式分解(18题型+真题过关)(解析版+原卷版),文件包含专题02整式与因式分解18题型+真题过关原卷版docx、专题02整式与因式分解18题型+真题过关解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
专题02 整式乘法公式的4种压轴题型全攻略-七年级数学上册压轴题攻略(沪教版): 这是一份专题02 整式乘法公式的4种压轴题型全攻略-七年级数学上册压轴题攻略(沪教版),文件包含专题02整式乘法公式的4种压轴题型全攻略原卷版docx、专题02整式乘法公式的4种压轴题型全攻略解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。













