初中湘教版1.2 二次函数的图像与性质课文配套ppt课件

这是一份初中湘教版1.2 二次函数的图像与性质课文配套ppt课件，共29页。PPT课件主要包含了位置开口方向，对称性，顶点最值，增减性，开口向上在x轴上方，开口向下在x轴下方，a越大开口越小，图形F也是抛物线，F开口向上，直线xh等内容，欢迎下载使用。

1.会用描点法画出y=a（x-h）2的图象.2.掌握二次函数y=a（x-h）2的图象与性质并会应用.
门禁反映了图形的平移，大家还记得平移的要点吗？
平移不改变图形的形状和大小
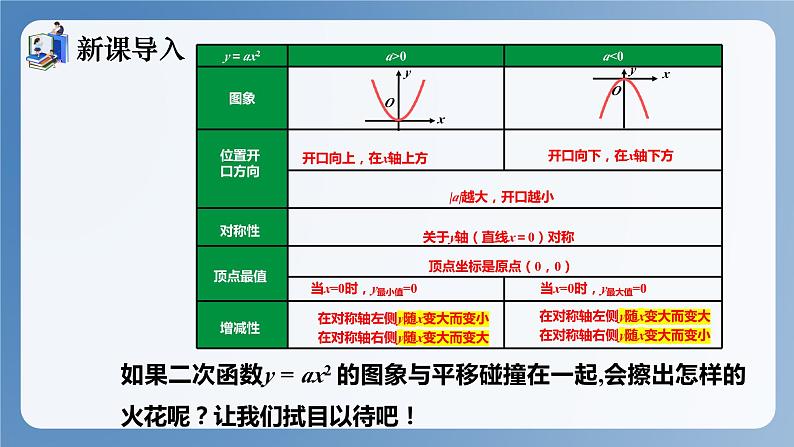
羽毛球的运动轨迹可以用y = ax2 的图象刻画,大家能回忆出二次函数 y = x2的性质吗？
关于y轴（直线x＝0）对称
顶点坐标是原点（0，0）
当x=0时，y最小值=0
当x=0时，y最大值=0
在对称轴左侧y随x变大而变小在对称轴右侧y随x变大而变大
在对称轴左侧y随x变大而变大在对称轴右侧y随x变大而变小
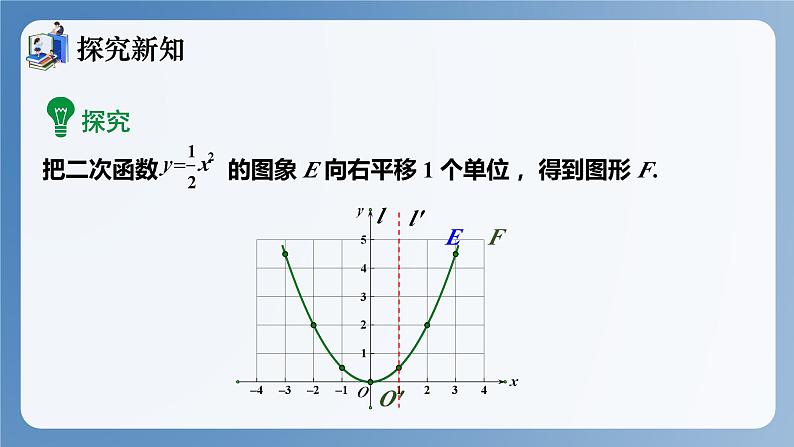
如果二次函数y = ax2 的图象与平移碰撞在一起,会擦出怎样的火花呢？让我们拭目以待吧！
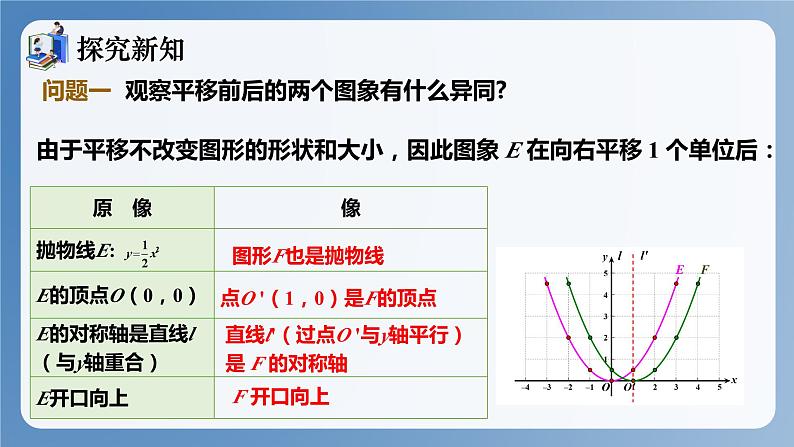
由于平移不改变图形的形状和大小，因此图象 E 在向右平移 1 个单位后：
点O '（1，0）是F的顶点
直线l'（过点O '与y轴平行）是 F 的对称轴
问题一 观察平移前后的两个图象有什么异同?
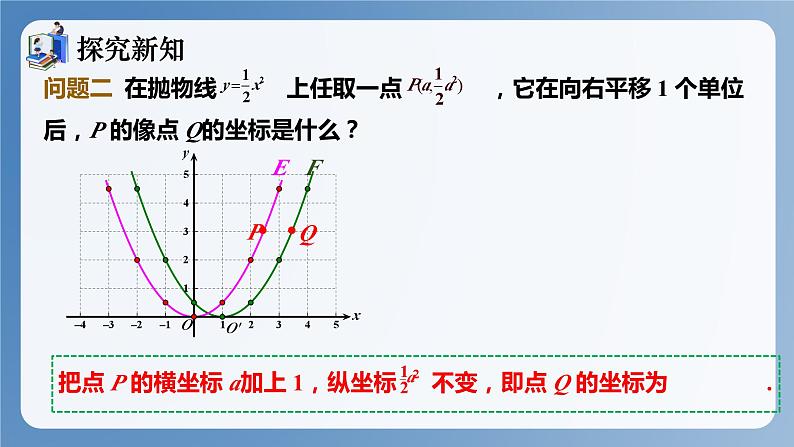
问题二 在抛物线 上任取一点 ，它在向右平移 1 个单位后，P 的像点 Q的坐标是什么？
把点 P 的横坐标 a加上 1，纵坐标 不变，即点 Q 的坐标为 .
记 b ＝ a + 1， 则 a ＝b -1， 从而点 Q 的坐标为（b，(b-1)2）. 这表明： 点 Q 在函数 的图象上． 由此得出， 抛物线 F 是函数 的图象．
问题三 抛物线 F 是哪个函数的图象呢？
xh 时,y 随x的增大而增大.
xh时,y随 x的增大而减小.
x=h时，y最小值=0.
x=h时，y最大值=0.
二次函数y=a(x-h)2 (a≠0) 的图象和性质
由于我们已经知道了二次函数 y ＝ a（x - h ）2 的图象的性质， 因此今后在画 y ＝ a（x - h ）2 的图象时， 只要先画出对称轴以及图象在对称轴右边的部分， 然后利用对称性， 画出图象在对称轴左边的部分．在画右边部分时， 只需“列表、描点、连线” 三个步骤.
抛物线 有何关系？
①抛物线 向____平移___个单位长度，就得到抛物线 ； ②抛物线 向____平移____个单位长度，就得到抛物线 ；
③抛物线 向____平移___个单位长度，就得到抛物线 ； ④抛物线 向____平移____个单位长度，就得到抛物线 ；
③抛物线 向____平移___个单位长度，就得到抛物线 ； ④抛物线 向____平移____个单位长度，就得到抛物线 ；
二次函数y=a(x-h)2（a≠0）与y=ax2 （a≠0）的图象的关系
向左平移h个单位
向右平移h个单位
例1 画函数 y ＝ （ x － 2 ）2 的图象．
解 抛物线 y =（x - 2）2 的对称轴是 x = 2，顶点坐标是（2，0）.
列表：自变量 x 从顶点的横坐标 2 开始取值.
描点和连线：画出图象在对称轴右边的部分．利用对称性， 画出图象在对称轴左边的部分．这样就得到了 y ＝（ x－2 ）2的图象.
y ＝( x－2 )2
例2 已知函数 .(1)请画出它的图像
（2）描点（3）连线，用平滑的曲线 画出三个函数的图象
（2）写出该二次函数图象的对称轴和顶点坐标；
解：对称轴为x=1 顶点坐标为（1,0）
（3）当x取何值时，y随x的增大而增大？
解：当x>1时，y随x的增大而增大.
（4）若 3 ≤ x ≤ 5，求y的取值范围；
解：∵当x>1时，y随x的增大而增大，当x=3时，y=2； 当x=5时，y=8，当3 ≤ x ≤ 5时，2 ≤ y ≤ 8
想一想：若-1 ≤ x ≤ 5，求y的取值范围
解：∵当-1 ≤ x ≤ 5时，y的最小值为0， ∴当-1 ≤ x ≤ 5时，y的取值范围是0 ≤ y ≤ 8
注意：限定了自变量的取值范围求函数值的范围时，应结合图象根据增减性在自变量取值范围内取最值
（6）若 抛物线上有两点A(x1,y1),B(x2,y2),且x1＜x2，试比较y1与y2的大小.
解：当x1＜x2 ≤ 1时，y随x的增大而减小，∴y1>y2当x1>x2 ≥ 1时，y随x的增大而增大，∴y1＞y2
1. 抛物线 先向左平移3个单位长度后，得到的解析式为________， 再向右平移2个单位长度为_________.2.抛物线y=ax2 向右平移3个单位长度后经过点（-1,4），求a的值和平移后的函数解析式.解：抛物线y=ax2向右平移3个单位长度后，得到的抛物线为y=a(x -3)2，把x=-1,y=4代入，得4=a(-1-3)2,解得∴平移后的函数解析式为
3.把抛物线y=－x2沿着x轴方向平移3个单位长度，那么平移后抛物线的解析式是 .
y= - (x+3)2 或 y=-(x－3)2
4. 已知函数y=-2(x -2)2.(1)当x取何值时，y随x的增大而减小？解：∵函数对称轴为x =2，且开口向下 ∴当x＞2时，y随x的增大而减小.
(2)当A(1，a),B(2,b),C(4,c)在抛物线y=-2(x -2)2上时，求a,b,c的大小关系.
解法1 代数法：代数法：将 1，2，4分别代入函数解析式，求出a=-2，b=0 ，c= -8 ,进而比较大小.
解法2 对称性：∵函数对称轴为x =2，且开口向下∴b是函数的最大值，且A(1，a)关于x =2的对称点为(3，a)，∴b > a > c
解法3 数形结合法：
因为y=-2(x -2)2，所以a=-2<0 ,所以图象开口朝上，由三点的横坐标可以知道三点与对称轴的距离，明确三点的大致位置，从而画出草图：
5. 画出在平面直角坐标系中，函数 y=ax-1 与 y= - (x-a)2 的图象大致是图中的 （ ）
xh 时,y 随 x的增大而增大.
x h时，y 随 x的增大而减小.
二次函数y=a(x-h)2（a≠0）与y=ax2 的图象的关系