

2023-2024学年苏科版七年级数学上册期末复习压轴题之选择压轴题专项训练(含答案解析)
展开姓名:_________班级:_________学号:_________
1.如图,已知数轴上点A、B、C所对应的数a、b、c都不为0,且C是AB的中点,如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0,则原点O的大致位置在( )
A.A的左边B.A与C之间C.C与B之间D.B的右边
2.下列说法正确的有( )
①已知a,b,c是非零的有理数,且|abc|abc=-1时,则|a|a+|b|b+|c|c的值为1或-3;
②已知a,b,c是有理数,且a+b+c=0,abc<0时,则b+c|a|+a+c|b|+a+b|c|的值为-1或3;
③已知x≤4时,那么x+3-x-4的最大值为7,最小值为-7;
④若a=b且|a-b|=23,则式子a+b-abb2+1的值为110;
⑤如果定义a,b=a+b(a>b)0a=bb-a(a
A.2个B.3个C.4个D.5个
3.已知有理数a,c,若a-2=18,且3a-c=c,则所有满足条件的数c的和是( )
A.﹣6B.2C.8D.9
4.|x﹣2|+|x﹣4|+|x﹣6|+|x﹣8|的最小值是a,|a|a+|b|b+|c|c=-1,那么|ab|ab+|bc|bc+|ac|ac+|abc|abc的值为( )
A.﹣2B.﹣1C.0D.不确定
5.如果四个互不相同的正整数m、n、p、q满足4-m4-n4-p4-q=9,则4m+3n+3p+q的最大值为( )
A.40B.53C.60D.70
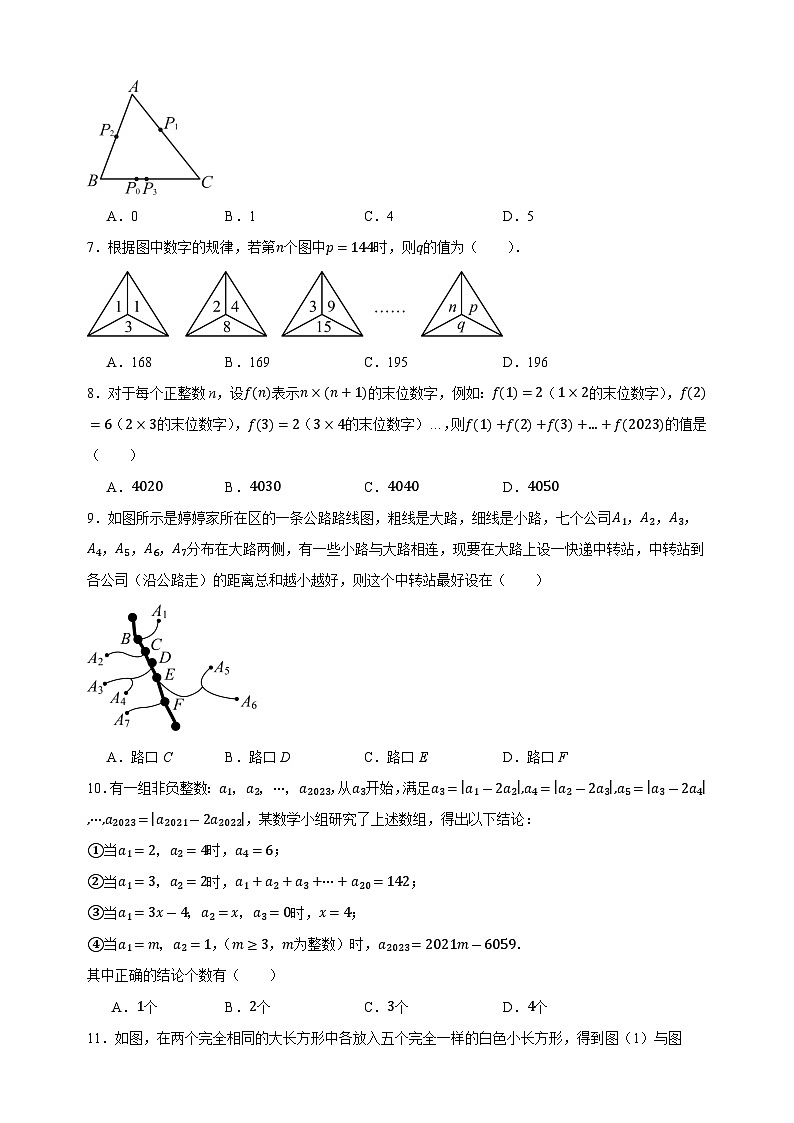
6.电子跳蚤游戏盘(如图)为三角形ABC,AB=10,BC=11,AC=12,如果电子跳蚤开始时在BC边的P0点,BP0=4,第一步跳蚤从P0跳到AC边上P1点,且CP1=CP0;第二步跳蚤从P1跳到AB边上P2点,且AP2=AP1;第三步跳蚤从P2跳回到BC边上P3点,且BP3=BP2;…跳蚤按上述规则跳下去,第n次落点为Pn,则P4与P2023之间的距离为( )
A.0B.1C.4D.5
7.根据图中数字的规律,若第n个图中p=144时,则q的值为( ).
A.168B.169C.195D.196
8.对于每个正整数n,设fn表示n×n+1的末位数字,例如:f1=2(1×2的末位数字),f2=6(2×3的末位数字),f3=2(3×4的末位数字)…,则f1+f2+f3+…+f2023的值是( )
A.4020B.4030C.4040D.4050
9.如图所示是婷婷家所在区的一条公路路线图,粗线是大路,细线是小路,七个公司A1,A2,A3,A4,A5,A6,A7分布在大路两侧,有一些小路与大路相连,现要在大路上设一快递中转站,中转站到各公司(沿公路走)的距离总和越小越好,则这个中转站最好设在( )
A.路口CB.路口DC.路口ED.路口F
10.有一组非负整数:a1,a2,⋯,a2023,从a3开始,满足a3=a1-2a2,a4=a2-2a3,a5=a3-2a4,⋯,a2023=a2021-2a2022,某数学小组研究了上述数组,得出以下结论:
①当a1=2,a2=4时,a4=6;
②当a1=3,a2=2时,a1+a2+a3+⋯+a20=142;
③当a1=3x-4,a2=x,a3=0时,x=4;
④当a1=m,a2=1,(m≥3,m为整数)时,a2023=2021m-6059.
其中正确的结论个数有( )
A.1个B.2个C.3个D.4个
11.如图,在两个完全相同的大长方形中各放入五个完全一样的白色小长方形,得到图(1)与图(2).若AB=m,则图(1)与图(2)阴影部分周长的差是( )
A.mB.54mC.65mD.76m
12.对任意代数式,每个字母及其左边的符号(不包括括号外的符号)称为一个数,如:a-b+c--d-e,其中称a为“数1”,b为“数2”,+c为“数3”,-d为“数4”,-e为“数5”,若将任意两个数交换位置,则称这个过程为“换位思考”,例如:对上述代数式的“数1”和“数5”进行“换位思考”,得到:-e-b+c--d+a,则下列说法中正确的个数是( )
①代数式a-b+c-d-e进行一次“换位思考”,化简后只能得到1种结果
②代数式a-b+c-d-e进行一次“换位思考”,化简后可能得到5种结果
③代数式a+b-c-d-e进行一次“换位思考”,化简后可能得到7种结果
④代数式a-b+c-d-e进行一次“换位思考”,化简后可能得到8种结果
A.0B.2C.3D.4
13.有依次排列的两个整式:x,x-2,对任意相邻的两个整式,都用左边的整式减去右边的整式,所得的差写在这两个整式之间,可以产生一个新的整式串:x,2,x-2,这称为第一次操作;将第一次操作后的整式串按上述方式再做一次操作,可以得到第二次操作后的整式串:x,x-2,2,4-x,x-2,以此类推.通过实际操作,小南同学得到以下结论:①第二次操作后,当x<2时,所有整式的积为正数;②第三次操作后整式串共有9个整式;③第n次操作后整式串共有2n+1个整式(n为正整数);④第2023次操作后,所有的整式的和为2x+4044.四个结论正确的有( )
A.1个B.2个C.3个D.4个
14.如图,大长方形ABCD是由一张周长为C1正方形纸片①和四张周长分别为C2,C3,C4,C5的长方形纸片②,③,④,⑤拼成,若大长方形周长为定值,则下列各式中为定值的是( )
A.C1B.C3+C5C.C1+C3+C5D.C1+C2+C4
15.我们把不超过有理数x的最大整数称为x的整数部分,记作x,又把x-x称为x的小数部分,记作x,则有x=x+x.如:1.3=1,1.3=0.3,1.3=1.3+1.3,.下列说法中正确的有( )个
①2.8=2;
②-5.3=-5;
③若1
A.1B.2C.3D.4
16.关于x的方程2x=ax+5有整数解,则整数a的所有可能取值的乘积为( )
A.9B.-3C.1D.3
17.已知整数a使关于x的方程x-2-ax4=x+22-1有整数解,则符合条件的所有a值的和为( )
A.﹣8B.﹣4C.﹣7D.﹣1
18.如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始匀速运动,甲按顺时针方向运动,乙按逆时针方向运动,若乙的速度是甲的3倍,那么它们第一次相遇在AD边上,请问它们第2023次相遇在哪条边上?( )
A.ADB.CDC.BCD.AB
19.如图,已知A,B(B在A的左侧)是数轴上的两点,点A对应的数为8,且AB=12,动点P从点A出发,以每秒2个单位长度的速度沿数轴向左运动,在点P的运动过程中,M,N始终为AP,BP的中点,设运动时间为tt>0秒,则下列结论中正确的有( )
①点B对应的数是-4;②点P到达点B时,t=6;
③BP=2时,t=5; ④在点P的运动过程中,线段MN的长度不变.
A.2个B.1个C.4个D.3个
20.如图,A、O、B两点在数轴上对应的数分别为﹣20、0、40,C点在A、B之间,在A、B两点处各放一个挡板,M、N两个小球同时从C处出发,M以2个单位/秒的速度向数轴负方向运动,N以4个单位/秒的速度向数轴正方向运动,碰到挡板后则反方向运动,速度大小不变.设两个小球运动的时间为t秒钟(0<t<40),当M小球第一次碰到A挡板时,N小球刚好第一次碰到B挡板.则:①C点在数轴上对应的数为0;②当10<t<25时,N在数轴上对应的数可以表示为80﹣4t;③当25<t<40时,2MA+NB始终为定值160;④只存在唯一的t值,使3MO=NO,以上结论正确的有( )
A.①②③④B.①③C.②③D.①②④
21.如图,长方形ABCD中,AB=8cm,AD=6cm,P,Q两动点同时出发,分别沿着长方形的边长运动,P点从B点出发,顺时针旋转一圈,到达B点后停止运动,Q点的运动路线为B→C→D,P,Q点的运动速度分别为2cm/秒,1cm/秒,当一个动点到达终点时,另一个动点也同时停止运动.设两动点运动的时间为t秒,要使△BDP和△ACQ的面积相等,满足条件的t值的个数为( )
A.2B.3C.4D.5
22.如图,在数轴上,点P表示-1,将点P沿数轴做如下移动,第一次点P向右平移2个单位长度到达点P1,第二次将点P1向左移动4个单位长度到达P2,第三次将点P2向右移动6个单位长度,按照这种移动规律移动下去,第n次移动到点Pn,给出以下结论:①P5表示5;②P12>P11;③若点Pn到原点的距离为15,则n=15;④当n为奇数时,Pn-Pn-1=2Pn;以上结论正确的是( )
A.①②③B.①②④C.②③D.①④
23.已知点A在数轴上对应的数为a,点B对应的数为b,且a+2+b-12=0,A、B之间的距离记作AB,定义:AB=a-b.下列结论:①线段AB的长AB=3;②设点P在数轴上对应的数为x,当PA-PB=2时,x=0.5;③若点P在A的左侧,PA+PB<3;④若点P在线段AB上,则PA+PB的值不变.其中正确的是( )
A.①②③B.①②④C.①③D.①④
24.如图,A点的初始位置在数轴上表示1的点上,先对A做如下移动:第一次向右移动3个单位长度到达点B,第二次从B点出发向左移动6个单位长度到达点C,第三次从C点出发向右移动9个单位长度到达点D,第四次从D点出发向左移动12个单位长度到达点E,…….以此类推,按照以上规律第( )次移动到的点到原点的距离为20
A.7B.10C.14D.19
25.已知A,B两点在数轴上的位置如图所示,原点为O,现A点以2m/s的速度向左运动,B点以1m/s的速度向左运动,若A,B两点同时出发,当OA:OB=1:2时,用时为( )
A.2sB.14sC.73s或1sD.12s或2s
26.点A,B是数轴上两点,位置如图,点P,Q是数轴上两动点,点P由点A点出发,以1单位长度/秒的速度在数轴上运动,点Q由点B点出发,以2单位长度/秒的速度在数轴上运动.若两点同时开始和结束运动,设运动时间为t秒.下面是四位同学的判断:
①小康同学:当t=2时,点P和点Q重合.
②小柔同学:当t=6时,点P和点Q重合.
③小议同学:当t=2时,PQ=8.
④小科同学:当t=6时,PQ=18.
以上说法可能正确的是( )
A.①②③B.②③④C.①③④D.①②③④
27.数轴上点A,O,B,C分别表示实数-4,0,2,3,点M,N分别从A,O出发,沿数轴正方向移动,点P从B出发,在线段BC上往返运动(P在B,C处掉头的时间忽略不计),三个点同时出发,点M,N,P的速度分别为2,1,1个单位长度每秒,点M,N重合时,运动停止.当点P为线段MN的中点时,运动时间t为( )
A.2B.165C.72D.165或72
28.用火柴棒按下列方式搭图形,有下列说法:
①第4个图形需要22根火柴棒;
②第5个图形共有10个小正方形;
③用112根火柴棒,按所给方式可以依次搭出6个图形;
④如果某一图形共用了2022根火柴棒,那么它是第404个图形.
其中正确的是( )
A.①②③B.①②④C.①③④D.②③④
29.如图所示,B在线段AC上,且BC=3AB,D是线段AB的中点,E是线段BC上的一点BE:EC=2:1,则下列结论:①EC=13AE;②DE=5BD;③BE=12(AE+BC);④AE=65(BC-AD),其中正确结论的有( )
A.①②B.①②④C.②③④D.①②③④
30.如图,A,B两地相距1200m,小车从A地出发,以8m/s的速度向B地行驶,中途在C地停靠3分钟.大货车从B地出发,以5m/s的速度向A地行驶,途经D地(在A地与C地之间)时沿原路返回B点取货两次,且往返两次速度都保持不变(取货时间不计),取完两批货后再出发至A点.已知:AC=3BC,CD=100m,则直至两车都各自到达终点时,两车相遇的次数为( )
A.2B.3C.4D.5
31.如图,点M在线段AN的延长线上,且线段MN=10,第一次操作:分别取线段AM和AN的中点M1、N1;第二次操作:分别取线段AM1和AN1的中点M2,N2;第三次操作:分别取线段AM2和AN2的中点M3,N3;…连续这样操作2023次,则每次的两个中点所形成的所有线段之和M1N1+M2N2+⋅⋅⋅+M2023N2023=( )
A.10+522022B.10+522023C.10-522022D.10-522023
32.已知点C在线段AB上,AC=2BC,点D,E在线段AB上,点D在点E的左侧.若AB=2DE,线段DE在线段AB上移动,且满足关系式AD+ECBE=32,则CDCB的值为( )
A.5B.1714C.1714或56D.1110
33.如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒).若点P在运动过程中,当PB=2时,则运动时间t的值为( )
A.32秒或72秒B.32秒或72秒或132或172秒
C.3秒或7秒D.3秒或132或7秒或172秒
34.一副三角板ABC、DBE,如图1放置,(∠D=30°、∠BAC=45°),将三角板DBE绕点B逆时针旋转一定角度,如图2所示,且0°<∠CBE<90°,有下列四个结论:
①在图1的情况下,在∠DBC内作∠DBF=∠EBF,则BA平分∠DBF;
②在旋转过程中,若BM平分∠DBA,BN平分∠EBC,∠MBN的角度恒为定值;
③在旋转过程中,两块三角板的边所在直线夹角成90°的次数为3次;
④∠DBC+∠ABE的角度恒为105°.
其中正确的结论个数为( )
A.1个B.2个C.3个D.4个
35.如图,点O为线段AD外一点,点M,C,B,N为AD上任意四点,连接OM,OC,OB,ON,下列结论不正确的是( )
A.以O为顶点的角共有15个
B.若MC=CB,MN=ND,则CD=2CN
C.若M为AB中点,N为CD中点,则MN=12AD-CB
D.若OM平分∠AOC,ON平分∠BOD,∠AOD=5∠COB,则∠MON=32∠MOC+∠BON
36.已知三条射线OA、OB、OC,若其中一条射线平分另两条射线所组成的角时,我们称OA、OB、OC组成的图形为“角分图形”.
如图(1),当OB平分∠AOC时,图(1)为角分图形.
如图(2),点O是直线MN上一点,∠DON=70°,射线OM绕点O以每秒5°的速度顺时针旋转至OM1,设时间为t0≤t≤36,当t为何值时,图中存在角分图形.小明认为t=29s,小亮认为t=11s,
你认为正确的答案为( )
A.小明B.小亮C.两人合在一起才正确D.两人合在一起也不正确
37.定义:从∠AOB的顶点出发,在角的内部引一条射线OC,把∠AOB分成1:2的两部分,射线OC叫做∠AOB的三等分线.若在∠MON中,射线OP是∠MON的三等分线,射线OQ是∠MOP的三等分线,设∠MOQ=x,则∠MON用含x的代数式表示为( )
A.94x或3x或92xB.94x或3x或9xC.94x或92x或9xD.3x或92x或9x
38.如图,在同一平面内,∠AOB=∠COD=90°,∠COE=∠BOE,点F为OE反向延长线上一点(图中所有角均指小于180°的角).下列结论:①∠AOE=∠DOE;②∠AOD+∠COB=180°;③∠COB-∠AOD=90°;④若OA绕点O顺时针旋转一周,其它条件都不变,若∠FOD:∠EOC=1:6,则∠FOD=18°或15°,其中结论一定正确的有( )个.
A.4个B.3个C.2个D.1个
39.如图,∠AOD=150°,∠BOC=30°,∠BOC绕点O逆时针在∠AOD的内部旋转,其中OM平分∠AOC,ON平分∠BOD,在∠BOC从OB与OA重合时开始到OC与OD重合为止,以每秒2°的速度旋转过程中,下列结论:
(1)射线OM的旋转速度为每秒2°;(2)当∠AON=90°时间为15秒;(3)∠MON的大小为60°;(4)在整个过程中∠BOC在∠MON内部持续时长为45秒.
其中正确的有( )个.
A.1B.2C.3D.4
40.如图,O是直线AC上的一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,且∠DOE=60°,∠BOE=13∠EOC.下列四个结论:①∠BOD=20°;②射线OE平分∠AOC;③图中与∠BOE互余的角有2个;④图中互补的角有6对.其中结论正确的序号有( )
A.①③④B.②③④C.②③D.②④
参考答案
1.B
【思路点拨】
可得a+b=2c,从而可得|a+b|-|a-2c|+|b-2c|-|a+b-2c|==|a+b|-|b|+|a|;然后根据选项判断a,b,a+b的符号,进行化简即可求解。
【解题过程】
解:C是AB的中点,∴a+b=2c
∴a+b-a-2c+b-2c-a+b-2c
=a+b-a-a+b+b-a+b-a+b-a+b
=a+b-b+a-0
=a+b-b+a;
A.在A的左边,∴a>0,b>0,a+b>0,
a+b-b+a
=a+b-b+a=2a≠0,
故此项不符合题意;
B.在A与C之间时,∴a<0,b>0,a+b>0,
a+b-b+a
=a+b-b-a=0,
故此项符合题意;
C.在C与B之间时,∴a<0,b>0,a+b<0,
a+b-b+a
=-a-b-b-a
=-2a-2b≠0,
故此项不符合题意;
D.在B的右边时,∴a<0,b<0,a+b<0,
a+b-b+a
=-a-b+b-a
=-2a≠0,
故此项不符合题意;
故选:B.
2.C
【思路点拨】
①由题意可得,abc<0,则a,b,c中有一个或三个值为负数,讨论求解即可;②由abc<0可得a,b,c中有一个值为负数,求解即可;③根据x≤4化简绝对值,然后求解即可;④由题意可得a=b或a=-b,分别求解即可;⑤根据题意可得a,b异号,分两种情况求解即可.
【解题过程】
解:①由|abc|abc=-1可得abc<0,a,b,c中有一个或三个值为负数,
当a<0,b>0,c>0时,|a|a+|b|b+|c|c=-1+1+1=1
当a<0,b<0,c<0时,|a|a+|b|b+|c|c=-1-1-1=-3
故①正确;
②由abc<0和a+b+c=0得a,b,c中有一个值为负数,
∴a+b=-c,a+c=-b,b+c=-a
∴-a|a|+-b|b|+-c|c|=1-1-1=-1,
故②错误;
③当-3≤x≤4时,x-4≤0,x+3≥0,
则x+3-x-4=x+3+x-4=2x-1,此时最大值为7,最小值为-7
当x<-3时,x-4≤0,x+3<0
则x+3-x-4=-x-3+x-4=-7
故③正确;
④由a=b可得a=b或a=-b
当a=b时,a-b=0与|a-b|=23矛盾,舍去;
当a=-b时,a-b=-2b,a+b=0且2b=23
解得a=13,b=-13或a=-13,b=13
则ab=-19,b2=19
a+b-abb2+1=1919+1=110
故④正确;
⑤由题意可得a,b异号,
当a<0,b>0时,a=-a,b=b,
由a>b可得-a>b,即a+b<0符合题意,此时a<0
当a>0,b<0时,a=a,b=-b
由a>b可得a>-b,即a+b>0,与a+b<0矛盾,舍去,
综上{a,b}=b-a
故⑤正确;
正确的个数为4
故选:C
3.D
【思路点拨】
根据绝对值的代数意义对a-2=18进行化简,a-2=18或a-2=-18,解得a=20或a=-16有两个解,分两种情况再对3a-c=c进行化简,继而有两个不同的绝对值等式,320-c=c和3-16-c=c,每个等式同样利用绝对值的代数意义化简,分别得到c的值有两个,故c共有四个值,再进行相加,得到所有满足条件的数的和.
【解题过程】
解:∵a-2=18,
∴a-2=18或a-2=-18,
∴a=20或a=-16,
当a=20时,3a-c=c等价于320-c=c,即60-3c=c,
∴60-3c=c或60-3c=-c,
∴c=15或c=30;
当a=-16时,3a-c=c等价于3-16-c=c,即-48-3c=c,
∴-48-3c=c或-48-3c=-c,
∴c=-12或c=-24,
故c=15或c=30或c=-12或c=-24,
∴所有满足条件的数c的和为:15+30+(-12)+(-24)=9.
故答案为:D
4.C
【思路点拨】
根据绝对值的意义,先求出a的值,然后进行化简,得到|b|b+|c|c=-2,则b<0,c<0,再进行化简计算,即可得到答案.
【解题过程】
解:∵|x﹣2|+|x﹣4|+|x﹣6|+|x﹣8|的最小值是a,
∴当x=5时,|x﹣2|+|x﹣4|+|x﹣6|+|x﹣8|有最小值8,
∴a=8,
∵|a|a+|b|b+|c|c=-1,
∴|8|8+|b|b+|c|c=-1,
∴|b|b+|c|c=-2,
∴|b|b=-1,|c|c=-1,
∴b<0,c<0,
∴bc>0
∴|ab|ab+|bc|bc+|ac|ac+|abc|abc
=|8b|8b+|bc|bc+|8c|8c+|8bc|8bc
=|b|b+|bc|bc+|c|c+|bc|bc
=-2+|bc|bc+|bc|bc
=-2+1+1
=0;
故选:C.
5.B
【思路点拨】
由题意确定出m、n、p、q的值,代入原式计算即可求出值.
【解题过程】
解:∵四个互不相同的正整数m、n、p、q,满足4-m4-n4-p4-q=9,
∴要求4m+3n+3p+q的最大值,即m最大,4-m最小,则有:4-m=-3,4-n=1,4-p=-1,4-q=3,
解得:m=7,n=3,p=5,q=1,
则4m+3n+3p+q=53.
故选:B.
6.B
【思路点拨】
本题考查了数字的规律探究.先写出前几步的线段长度,然后推导出一般性规律是解题的关键.
由题意知,BP0=4,则CP0=11-4=7;第一步跳蚤从P0到P1,CP1=CP0=7;AP1=12-7=5;第二步跳蚤从P1到P2,AP2=AP1=5;BP2=10-5=5;第三步跳蚤从P2到P3,BP3=BP2=5;CP3=11-5=6;第四步跳蚤从P3到P4,CP4=CP3=6;AP4=12-6=6;第五步跳蚤从P4到P5,AP5=AP4=6;BP5=10-6=4;第六步跳蚤从P5到P6,BP6=BP5=4;CP6=11-4=7;第七步跳蚤从P6到P7,CP7=CP6=7;……可知每6步循环一次,由2023=6×337+1,可知第2023次落点P2023与P1重合,即P4与P2023之间的距离为P4与P1之间的距离,由P4与P1在AC上,根据CP1-CP4,计算求解即可.
【解题过程】
解:由题意知,BP0=4,则CP0=11-4=7;
第一步跳蚤从P0到P1,CP1=CP0=7;AP1=12-7=5;
第二步跳蚤从P1到P2,AP2=AP1=5;BP2=10-5=5;
第三步跳蚤从P2到P3,BP3=BP2=5;CP3=11-5=6;
第四步跳蚤从P3到P4,CP4=CP3=6;AP4=12-6=6;
第五步跳蚤从P4到P5,AP5=AP4=6;BP5=10-6=4;
第六步跳蚤从P5到P6,BP6=BP5=4;CP6=11-4=7;
第七步跳蚤从P6到P7,CP7=CP6=7;
……
∴每6步循环一次,
∵2023=6×337+1,
∴第2023次落点P2023与P1重合,即P4与P2023之间的距离为P4与P1之间的距离,
∵P4与P1在AC上,
∴CP1-CP4=7-6=1,
故选:B.
7.A
【思路点拨】
在“n”区域的规律是第n个图:n,在“P”区域的规律是第n个图:P=n2,在“q”区域的规律是:第n个图:q=n+12-1;由p=144,可求出n=12,代入q的规律即可求解.
【解题过程】
解:由图得
在“n”区域的规律是:
第1个图:1,
第2个图:2,
第3个图:3,
⋯
第n个图:n;
在“P”区域的规律是:
第1个图:1,
第2个图:22,
第3个图:32,
⋯
第n个图:P=n2;
在“q”区域的规律是:
第1个图:1+12-1,
第2个图:2+12-1,
第3个图:3+12-1,
⋯
第n个图:q=n+12-1;
当p=144时,
n2=144,
∴n=12,
∴q=12+12-1
=165;
故选:A.
8.D
【思路点拨】
本题考查数字的变化类,根据题意,可以写出前几个式子的值,然后即可发现式子的变化特点,从而可以求得所求式子的值.解答本题的关键是明确题意,发现式子的变化特点,求出所求式子的值.
【解题过程】
解:由题意可得,
因为f1=2,f2=6,
所以f1+f2=2+6=8,
以此类推,得
f1+f2+f3=2+6+2=10,
f1+f2+f3+f4=2+6+2+0=10,
f1+f2+f3+f4+f5=2+6+2+0+0=10,
f1+…+f5+f6=2+6+2+0+0+2=12,
f1+…+f5+f6+f7=2+6+2+0+0+2+6=18,
f1+…+f7+f8=2+6+2+0+0+2+6+2=20,
f1+…+f7+f8+f9=2+6+2+0+0+2+6+2+0=20,
f1+…+f7+f8+f9+f10=2+6+2+0+0+2+6+2+0+0=20
……
∵2023÷5=404…3,
∴f1+f2+f3+…+f2023
=2+6+4+0+0+2+6+4+0+0+…+2+6+4+0+0+2+6+4
=10×404+10
=4040+10
=4050,
故选:D.
9.B
【思路点拨】
本题主要考查了实际问题中的大小比较,列代数式,整式的加减,根据给定图形,用d表示7个公司到大公路最近的小公路距离和,BC=d1,CD=d2,DE=d3,EF=d4,再求出到路口C,D,E,F的距离总和,比较大小作答.
【解题过程】
解∶观察图形知,A1,A2,A3,A4,A5,A6,A7七个公司要到中转站,先都必须沿小公路走到小公路与大公路的连接点,
令A1到B、A2到C、A3到D、A4到D、A5到E、A6到E、A7到F的小公路距离总和为d,BC=d1,CD=d2,DE=d3,EF=d4,
路口C为中转站时,距离总和SC=d+d1+d2+d2+d3+d2+d3+d2+d4+d3+d2=d+d1+5d2+3d3+d4.
路口D为中转站时,距离总和SD=d+d1+d2+d2+d3+d3+d4+d3=d+d1+2d2+3d3+d4.
路口E为中转站时,距离总和SE=d+d1+d2+d3+d2+d3+d3+d3+d4=d+d1+2d2+4d3+d4.
路口F为中转站时,距离总和SF=d+d1+d2+d3+d4+d2+d3+d4+2d3+d4+2d4=d+d1+2d2+4d3+5d4,
∴SC>SD,SF>SE>SD,
∴这个中转站最好设在路口D.
故选∶ B.
10.B
【思路点拨】
根据其规律,求出其值,再判定结论错误与否.
【解题过程】
解:根据题意有,①当a1=2,a2=4时,a3=6,a4=8,故①结论错误;
②当a1=3,a2=2时,a3=1,a4=0,a5=1,a6=2,a7=3,a8=4, a9=5,a10=6,a11=7,a12=8,⋯,a20=16,
∴a1+a2+a3+⋯+a20=3+2+1+0+1+2+3+⋯+16,
=6+16×172,
=142,
故②结论正确;
③当a1=3x-4,a2=x,a3=0时,则有:3x-4-2x=0,
解得:x=4,故③结论正确;
④当a1=m,a2=1(m≥3,m为整数)时,a3=m-2,a4=2m-5,a5=3m-8,a6=4m-11,⋯,an=n-2m-3n+7,
∴a2023=2021m-6062,
故④结论错误;
综上所述,正确的结论个数为2个,
故选:B.
11.C
【思路点拨】
设小长方形的宽为x,长为y,大长方形的宽为n,表示出x、y、m、n之间的关系,然后求出阴影部分周长之差即可.
【解题过程】
解:设小长方形的宽为x,长为y,大长方形的宽为n,
由图(1)得4x=n;
由图(2)得2x+y=m,y=3x;
∴5x=m,
∴x=m5,
图(1)中阴影部分的周长为:2n+2y+m-y+m-y-x+x=2n+2m=8x+2m=185m,
图(2)中阴影部分的周长为:2n-3x+2m=24x-3x+2m=2x+2m=125m,
∴阴影部分的周长之差为:185m-125m=65m,
故选:C.
12.C
【思路点拨】
根据括号外面是“+”,去括号不改变括号里面式子的符号;括号外面是“-”,去括号改变括号里面式子的符号;依此即可求解.
【解题过程】
解:在代数式a-b+c-d-e中,将任意两个数交换位置,均不会改变每个数的符号,故化简后只能得到一种结果,均为a-b+c-d-e,故①正确;
代数式a-b+c-d-e中,有两种情况:
(1)括号内四个数任意两个交换位置,化简后的结果不变,故只有一种结果,为a-b-c+d+e;
(2)当a分别与括号内的四个数换位思考,化简后得到4种结果分别为:
-a+b-c+d+e;-a-b+c+d+e;-a-b-c-d+e;-a-b-c+d-e.
故该代数式共得到5种结果,故②正确;
代数式a+b-c-d-e中,有三种情况:
(1)a与b进行换位思考以及c,-d,-e三个数中任意两个进行换位思考,化简后只有1种结果,均为:a+b-c+d+e;
(2)a与c,-d,-e分别进行换位思考,化简后得到3种结果,分别为:
-a+b+c+d+e,-a+b-c-d+e,-a+b-c+d-e;
(3)b与c,-d,-e分别进行换位思考,化简后得到3种结果,分别为:a-b+c+d+e,a-b-c-d+e,a-b-c+d-e,故该函代数式共得到7种结果,故③正确;
代数式a-b+c-d-e中,有三种情况:
(1)b与c换位思考及d与-e换位思考,化简后只有1种结果:a-b-c+d-e;
(2)a分别与b和c换位思考,得到2种结果;分别为:-a+b-c+d-e,-a-b+c+d-e;
(3)a分别与d,-e换位思考,得到1种结果为a-b-c+d-e,此结果重复;
(4)b分别与d,-e换位思考,得到2种结果,分别为:a+b-c-d-e,a+b-c+d+e;
(5)c分别与d,-e换位思考,得到2种结果;分别为:a-b+c-d-e,a-b+c+d+e;
故该代数式共有7种结果,故④错误;
故选:C.
13.C
【思路点拨】
①根据第二次操作后,当x<2时,各个整式的正负,判断所有整式的积的正负:②根据第三次操作后整式的个数判定;③根据前四次操作结果,探究每次操作整式个数与操作次数关系的规律判定;④根据前四次操作结果,探究每次操作所有整式的和与操作次数关系的规律解答
【解题过程】
解:①原整式为:x,x-2,
第1次操作后所得整式串为:x,2,x-2,
第2次操作后所得整式串为:x,x-2,2,4-x,x-2,
此次所有整式之积为,2xx-224-x,
∵x<2,
∴当-2
∴2xx-224-x≤0,①不正确;
②第3次操作后所得整式串为:x,2,x-2,x-4,2,x-2,4-x,6-2x,x-2,共有9个整式,②正确;
③第1次操作后整式串共有3个整式,3=2+1,
第2次操作后整式串共有5个整式5=22+1,,
第3次操作后整式串共有9个整式,9=23+1,
第4次操作后整式串共有17个整式,17=24+1,
……,
第n次操作后整式串共有整式个数为:2n+1,③正确;
④第1次操作后所得整式串为:x,2,x-2,所有整式之和为:2x,
第2次操作后所得整式串为:x,x-2,2,4-x,x-2,所有整式之和为:2x+2,
第3次操作后所得整式串为:x,2,x-2,x-4,2,x-2,4-x,6-2x,x-2,所有整式之和为:2x+4,
第4次操作后所得整式串为:x,x-2,2,4-x,x-2,2,x-4,x-6,2,4-x,x-2,2x-6,4-x,x-2,6-2x,8-3x,x-2,所有整式之和为:2x+6,
……,
第n次操作后所得所有整式的和为:2x+2n-1,
故操作第2023次操作后所有整式之和为:2x+2×2013-1=2x+4044.④正确.
故选:C.
14.B
【思路点拨】
将各长方形的边长标记出来,可将大长方形ABCD的周长为C和正方形纸片①的周长C1和四张长方形纸片②,③,④,⑤的周长分别为C2,C3,C4,C5表示出来,其中大长方形ABCD的周长为C为定值,然后分别计算C3+C5,C1+C3+C5,C1+C2+C4,找出其中为定值的即可.
【解题过程】
解:如图,将各长方形的边长标记出来,
∴大长方形ABCD的周长为C=2a+2b+2c+2h为定值,
∴C2=2a+2b,C3=2c+2d,C4=2e+2f,C5=2h+2g,
∵①是正方形,
∴c-f=e-h=g-b=a-d
∴a+b=g+d,
∴C3+C5=2c+2d+2h+2g=2a+2b+2c+2h=C,
C1+C3+C5=4a-d+2c+2d+2h+2g=4a-2d+2c+2h+2g,
C1+C2+C4=4a-d+2a+2b+2e+2f=6a-4d+2b+2e+2f,
∴C3+C5为定值,
故选:B.
15.A
【思路点拨】
本题考查新定义,有理数的运算,方程的解.根据新定义判断①和②,求出x=1.4或x=-1.4时的x判断③,根据新定义得到4x=x+1,赋值法求方程的解判断④;本题的难度较大,属于选择题中的压轴题.
【解题过程】
解:由题意,得:2.8=2,故①正确;
-5.3=-6,故②错误;
当x=1.4时,1.4=1,1.4=1.4-1.4=0.4,
当x=-1.4时:-1.4=-2,-1.4=-1.4--2=0.6≠0.4;故③错误;
∵x=x+x,4x+1=x+3x
∴4x+1=x+3x+x,
∴4x=x+1
∵0≤x<1,
∴0≤4x<4,
∴当x=-1时,4x=0,x=0,此时x=-1;
x=0时,4x=1,x=0.25,此时x=0.25;
当x=1时,4x=2,x=0.5,此时x=1.5,
当x=2时,4x=3,x=0.75,此时x=2.75;
综上:4x+1=x+3x的解为x=0.25或x=2.75或x=-1或x=1.5;故④错误.
故选A.
16.A
【思路点拨】
分x≥0和x<0分别得到方程,再根据原方程有整数解求出a的值,再相乘即可.
此题主要考查一元一次方程解的情况,解题的关键是根据题意分类讨论求解.
【解题过程】
解:当x≥0时,原方程可化为2x=ax+5,
∴2-ax=5,
∵原方程有解∴a≠2,
∴x=52-a,
∵原方程有整数解x,a为整数,x≥0∴2-a=1或5,
∴a=1或-3,
当x<0时,原方程可化为-2x=ax+5,
∴-2+ax=5,
∵原方程有解∴a≠-2,
∴x=-52+a,
∵原方程有整数解x,a为整数,x<0
∴2+a=1或5,
∴a=-1或3,
综上所述,a的取值为±1、±3,
∴整数a的所有可能取值的乘积为9,
故选:A.
17.A
【思路点拨】
先求出方程的解是x=22+a,根据方程有整数解和a为整数得出2+a=1或2+a=-1或2+a=-2或2+a=2,求出a的值,再求出和即可.
【解题过程】
解:x-2-ax4=x+22-1,
去分母,得4x-2-ax=2x+2-4,
去括号,得4x-2+ax=2x+4-4,
移项,得4x+ax-2x=4-4+2,
合并同类项,得2+ax=2,
当2+a≠0时,x=22+a,
∵整数a使关于x的方程x-2-ax4=x+22-1有整数解,
∴2+a=1或2+a=-1或2+a=-2或2+a=2,
解得:a=-1或-3或-4或0,
和为-1+-3+-4+0=-8,
故选:A.
18.C
【思路点拨】
设出正方形的边长,甲的速度是乙的速度的3倍,求得每一次相遇的地点,找出规律即可解答.
【解题过程】
解:设正方形的边长为a,因为乙的速度是甲的速度的3倍,时间相同,甲乙所行的路程比为1:3,把正方形的每一条边平均分成2份,由题意知:
①第一次相遇甲乙行的路程和为2a,乙行的路程为2a×31+3=3a2,甲行的路程为2a×11+3=a2,在AD边的中点相遇;
②第一次相遇到第二次相遇甲乙行的路程和为4a,乙行的路程为4a×31+3=3a,甲行的路程为4a×11+3=a,在CD边的中点相遇;
③第二次相遇到第三次相遇甲乙行的路程和为4a,乙行的路程为4a×31+3=3a,甲行的路程为4a×11+3=a,在BC边的中点相遇;
④第三次相遇到第四次相遇甲乙行的路程和为4a,乙行的路程为4a×31+3=3a,甲行的路程为4a×11+3=a,在AB边的中点相遇;
⑤第四次相遇到第五次相遇甲乙行的路程和为4a,乙行的路程为4a×31+3=3a,甲行的路程为4a×11+3=a,在AD边的中点相遇;
四次一个循环,因为2023÷4=505⋯3,所以它们第2023次相遇在边BC上,
故选:C.
19.D
【思路点拨】
本题考查了数轴,①根据两点间距离进行计算即可;②利用路程除以速度即可;③分两种情况:当点P在点B右边时,当点P在点B左边时,分别求出AP的长,再利用路程除以速度即可;④分两种情况:当点P在点B右边时,当点P在点B左边时,利用线段的中点性质分别进行计算即可.
【解题过程】
解:设点B对应的数是x,
∵点A对应的数为8,且AB=12,
∴8-x=12,
∴x=-4,
∴点B对应的数是-4,
故①正确;
由题意得:12÷2=6(秒),
∴点P到达点B时,t=6,
故②正确;
当点P在点B右边时,
∵AB=12,BP=2,
∴AP=AB-BP=12-2=10,
∴10÷2=5(秒),
当点P在点B左边时,
∵AB=12,BP=2,
∴AP=AB+BP=12+2=14,
∴14÷2=7(秒),
综上,BP=2时,t=5或7;
故③错误;
∵M,N始终为AP,BP的中点,
∴MP=12AP,NP=12BP,
当点P在点B右边时,
MN=MP+NP
=12AP+12BP
=12AB
=12×12
=6,
当点P在点B左边时,
MN=MP-NP
=12AP-12BP
=12AB
=12×12
=6,
∴在点P的运动过程中,线段MN的长度不变,
故④正确;
所以,上列结论中正确的有3个,
故选:D.
20.D
【思路点拨】
设C点在数轴上对应的数为x,根据题意可得x+202=40-x4,求得x;根据题意分时间段讨论M、N两小球的位置,分别求解即可.
【解题过程】
解:设C点在数轴上对应的数为x,则CA=x+20,CB=40-x
当M小球第一次碰到A挡板时,N小球刚好第一次碰到B挡板,则x+202=40-x4
解得x=0,即C点在数轴上对应的数为0,①正确;
当t=10时,N小球运动的距离为4t=40,刚好到达B点,
当t=25时,N小球运动的距离为4t=100,刚好到达A点,M小球运动的距离为2t=50
当10<t<25时,N小球从B点向A点开始运动,此时BN=4(t-10),
点N表示数的为40-4(t-10)=80-4t,②正确;
当t=40时,N小球运动的距离为4t=160,M小球运动的距离为2t=80
当25<t<40时,N小球从A点向B点开始运动,M小球向B点运动
则MA=2t-20,NB=60-4(t-25)=160-4t,
2MA+NB=4t-40+160-4t=120,③错误;
当0
当10≤t<20时,MO=40-2t,ON=80-4t,
由题意3MO=NO得,3(40-2t)=80-4t,解得t=20,不符题意;
当20≤t<40时,MO=2t-40,
当20≤t<25时,NO=4t-80,
由题意3MO=NO得,3(2t-40)=4t-80,解得t=20,此时M、N、O三点重合,成立;
当25≤t<30时,NO=120-4t,
由题意3MO=NO得,3(2t-40)=120-4t,解得t=24,不符题意;
当30≤t<40时,NO=4t-120,
由题意3MO=NO得,3(2t-40)=4t-120,解得t=0,不符题意;
④正确
故选:D.
21.C
【思路点拨】
分五种情况,根据运动的路径和△BDP和△ACQ的面积相等列出方程,求解即可.
【解题过程】
解:由题意进行分类讨论:
①当P点在AB上,Q点在BC上时(t≤4),
BP=2t,CQ=6﹣t,
要使△BDP与△ACQ面积相等,则
12×2t×6=126-t×8,
解得:t=2.4;
②当P点在AD上,Q点在BC上时(4<t≤6),
DP=14﹣2t,CQ=6﹣t,
要使△BDP与△ACQ面积相等,则DP=CQ,
即14﹣2t=6﹣t,
解得:t=8(舍去);
③当P点在AD上,Q点在CD上时(6<t≤7),
DP=14﹣2t,CQ=t﹣6,
要使△BDP与△ACQ面积相等,则
12×814-2t=12×6t-6,
解得t=7411;
④当P点在CD上,Q点在CD上时(7<t≤11),
DP=2t﹣14,CQ=t﹣6,
要使△BDP与△ACQ面积相等,则DP=CQ,
即2t﹣14=t﹣6,
解得:t=8;
⑤当P点在BC上,Q点在CD上时(11<t≤14),
BP=28﹣2t,CQ=t﹣6,
要使△BDP与△ACQ面积相等,则
12×828-2t=12×6t-6,
解得:t=13011;
综上可得共有4种情况满足题意,所以满足条件的t值得个数为4.
故选:C.
22.D
【思路点拨】
先根据数轴的定义分别求出点P1,P2,P3,P4,P5,P6表示的数,再归纳类推出一般规律,然后逐个判断即可得.
【解题过程】
解:由题意,点P1表示的数为-1+2=1,
点P2表示的数为1-4=-3,
点P3表示的数为-3+6=3,
点P4表示的数为3-8=-5,
点P5表示的数为-5+10=5,
点P6表示的数为5-12=-7,
归纳类推得:当n为奇数时,Pn=n;当n为偶数时,Pn=-1n+1n+1,其中n为正整数,
则P5表示的数为5,结论①正确;
∵P11=11,P12=-112+1×12+1=-13,
∴P12
当n为偶数时,Pn=-1n+1n+1=n+1=15,解得n=14,
即若点Pn到原点的距离为15,则n=14或n=15,结论③错误;
当n为奇数时,Pn-Pn-1=n--1n-1+1n-1+1,
=n--1nn,
=n--1n,
=n+n,
=2n,
=2Pn,
即当n为奇数时,Pn-Pn-1=2Pn,结论④正确;
综上,结论正确的是①④,
故选:D.
23.B
【思路点拨】
①根据非负数的和为0,各项都为0确定a=-2,b=1,即可判断;②应考虑到A、B、P三点之间的位置关系的多种可能解题;③④利用②中的位置关系求解即可.
【解题过程】
解:①∵|a+2|+(b-1)2=0,
∴a=-2,b=1,
∴AB=|a-b|=3,即线段AB的长度为3.
故①正确;
②如图,分三种情况:
当P在点A左侧时,
|PA|-|PB|=-(PB-PA)=-|AB|=-3≠2.
当P在点B右侧时,
|PA|-|PB|=|AB|=3≠2.
∴上述两种情况的点P不存在.
当P在A、B之间时,-2≤x≤1,
∵|PA|=|x+2|=x+2,|PB|=|x-1|=1-x,
∴由|PA|-|PB|=2,得x+2-(1-x)=2.
∴解得:x=0.5;
∴当PA-PB=2时,x=0.5,
故②正确;
③由②得当P在点A左侧时,
PA+PB=AB+2PA=3+2PA>3,故③错误;
④当P在A、B之间时,-2≤x≤1,
PA+PB=x+2+1-x=3,
∴PA+PB的值不变,故④正确;
综合上述,①②④说法正确.
故选:B.
24.C
【思路点拨】
次数的序号为奇数的点在点A的右边,各点所表示的数依次增加3,序号为偶数的点在点A的左侧,各点所表示的数依次减少3,用n的代数式表示出一般规律,即可解答.
【解题过程】
解:第1次点A向右移动3个单位长度至点B,则B表示的数,1+3=4;
第2次从点B向左移动6个单位长度至点C,则C表示的数为4-6=-2;
第3次从点C向右移动9个单位长度至点D,则D表示的数为-2+9=7;
第4次从点D向左移动12个单位长度至点E,则E表示的数为7-12=-5;
第5次移动后表示的数为-5+15=10;
第6次移动后表示的数为10-18=-8;
…;
当移动次数为奇数时,对应的数是4,7,10,…,
第n次移动后表示的数是3n+52,
当3n+52=20时,
解得,n=353(不符合题意,舍去).
当移动次数为偶数时,对应的数是-2,-5,-8,…,
第n次移动后表示的数是-3n-22,
当-3n-22=-20时,
解得,n=14.
故选:C.
25.C
【思路点拨】
设A,B两点同时出发运动的时间为ts,分类讨论①当A点在O点右侧时和②当A点在O点左侧时,分别用t表示出OA和OB,再列出等式,解出t即可.
【解题过程】
解:设A,B两点同时出发运动的时间为ts,
分类讨论①当A点在O点右侧时,即t<32时,
此时OB=1+t,OA=3-2t,
∵OA:OB=1:2
∴(3-2t):(1+t)=1:2
解得:t=1<32,符合题意;
②当A点在O点左侧时,即t>32,
此时OB=1+t,OA=2t-3,
∵OA:OB=1:2
∴(2t-3):(1+t)=1:2
解得:t=73>32,符合题意.
综上可知t=1或t=73时,OA:OB=1:2
故选C.
26.A
【思路点拨】
由题意,先求出AB的长度,然后对P、Q两点的运动方向进行分析:当P、Q相向运动时可判断①;当点P在前,点Q在后运动可判断②;当点Q在前,点P在后可判断③;当P、Q反向运动或相向运动相遇后时,可判断④.
【解题过程】
解:根据题意,
∵点A表示-4,点B表示2,
∴AB=2-(-4)=6,
当点P、Q相向运动时,设t秒后P、Q重合,
∴(1+2)t=6,
∴t=2;故①正确;
当点P在前,点Q在后运动时,设t秒后P、Q重合,
(2-1)t=6,
∴t=6;故②正确;
当点Q在前,点P在后时,设t秒后PQ=8,
∴(2-1)t+6=8,
∴t=2;故③正确;
当P、Q反向运动时,设t秒后PQ=18,
∴(1+2)t+6=18,
∴t=4;
当P、Q两点相遇后再相距18,则
(1+2)t=18+6,
∴t=8;
∴④的说法错误;
∴正确的说法有①②③;
故选:A.
27.B
【思路点拨】
根据题意画出图形,t秒后,M点表示的数为-4+2t,N点表示的数为t,
设P点表示的数为p,根据题意得出p=3t2-2,然后根据当2
解:依题意,t秒后,M点表示的数为-4+2t,N点表示的数为t,
设P点表示的数为p,
当M,N相遇时,-4+2t=2,解得t=4,
∴相遇点在4,
∴当点P为线段MN的中点时,点N在点M的右侧,
∴t-p=p--4+2t
解得:p=3t2-2
∵点P从B出发,在线段BC上往返运动
∴2≤p≤3
∴2≤32t-2≤3
83
∴32t-2=t
解得:t=4(舍去)
当3
∴32t-2=6-t
解得:t=165,
故选:B.
28.B
【思路点拨】
根据前三个图形可得:第n个图形用了5n+2根火柴棒,共有2n个小正方形;然后根据规律逐一判断即得答案.
【解题过程】
解:第一个图形用了7根火柴棒,7=5×1+2,共有2个小正方形;
第二个图形用了12根火柴棒,12=5×2+2,共有4个小正方形;
第三个图形用了17根火柴棒,17=5×3+2,共有6个小正方形;
……,
所以第n个图形用了5n+2根火柴棒,共有2n个小正方形;
当n=4时,第4个图形需要5×4+2=22根火柴棒,故①正确;
当n=5时,第5个图形共有5×2=10个小正方形,故②正确;
若按所给方式依次搭出6个图形,则需要的火柴棒总数是7+12+17+22+27+32=117≠112,故③错误;
当5n+2=2022时,解得n=404,即它是第404个图形,故④正确;
综上,说法正确的是①②④;
故选:B.
29.B
【思路点拨】
根据题中的已知条件,结合图形,对结论进行一一论证,从而选出正确答案.
【解题过程】
解:∵E是BC的三等分点,BC=3AB,
∴EC=13BC,AB=13BC,
∴AB=EC,
∴AB+BE=EC+BE,
∴AE=BC,
∴EC=13AE,
故①正确;
∵EC=13AE,
∴AE=3EC,
∵AB=EC,
∴AE=3AB,
∵D是线段AB的中点,
∴AD=BD=12AB,
∴DE=AE-AD=3AB-12AB=52AB,
∴DE=52×2BD=5BD,
故②正确;
∵BE=2AB,AE=3AB
∴12AE+BC=123AB+3AB=3AB,
∵BE=AE-AB=3AB-AB=2AB,
∴BE12AE+BC=2AB3AB=23,
∴BE=23×12AE+BC=13AE+BC,
故③不正确;
∵BC=3AB,AD=12AB,
∴65BC-AD=653AB-12AB=3AB,
∵AE=3AB,
∴AE=65BC-AD,
故④正确;
综上,正确的有①②④,
故选:B.
30.A
【思路点拨】
由题意可求出AC=900m,BC=300m,CD=800m,BD=400m.再根据题意结合速度=路程÷时间讨论即可.
【解题过程】
解:由题意可知AB=1200m.
∵AC=3BC,
∴AC=34AB=900m,BC=14AB=300m,
∴AD=AC-CD=800m,BD=BC+CD=400m.
当大货车第一次到达D地时,用时4005=80s,
∴此时小车行驶路程为8×80=640m.
∵640+400=1040m<1200m,
∴此过程两车不相遇;
当大货车第一次由D地返回B地,且到达C地的过程中,
∵CD=100m,
∴大货车到达C地用时1005=20s.
假设此过程中两车相遇,且又经过t秒相遇,
则(900-640)-100+5t=8t,
解得:t=1603s>20s,即说明大货车到达C地之前没相遇;
当大货车继续由C地返回B地时,
∵BC=300m,
∴大货车到达B地用时3005=60s.
此时大货车共行驶80+20+60=160s.
∵小车到达C地用时9008=112.5s<160s,
∴当大货车到达B地时,小车已经到达C地停靠160-112.5=47.5s.
∵小车中途在C地停靠3分钟,即180s,
∴当大货车到达B地时,小车在C地还需停靠180-47.5=132.5s.
当大货车又从B地出发前往D地时,用时4005=80s,
∴当大货车到达D地时小车还在停靠,即此时第一次相遇,
∴此时小车剩余停靠时间132.5-80=52.5s,
∴当小车出发时,大货车第二次从D地前往B地行驶了52.5×5=262.5m.
假设大货车到达B地前小车能追上大货车,且用时为t1,
则262.5+5t1=8t1,
解得:t1=87.5s>80s,即说明大货车到达B地前小车没追上大货车,
∴此过程两车没相遇.
当大货车最后由B地前往A地时,小车正在向B地行驶,
∴两车此过程必相遇.
综上可知,两车相遇的次数为2次.
故选A.
31.C
【思路点拨】
根据MN=10,M1、N1分别为AM、AN的中点,求出M1N1的长度,再由M1N1的长度求出M2N2的长度,找到MnNn的规律即可求出M1N1+M2N2+⋅⋅⋅+M2023N2023的值.
【解题过程】
解:∵MN=10,M1、N1分别为AM、AN的中点,
∴M1N1=AM1-AN1=12AM-12AN=12AM-AN=12MN=12×10=5,
∵M2、N2分别为AM1、AN1的中点,
∴M2N2=AM2-AN2=12AM1-12AN1=12AM1-AN1=12M1N1=12×5=52,
∵M3、N3分别为AM2、AN2的中点,
∴M3N3=AM3-AN3=12AM2-12AN2=12AM2-AN2=12M2N2=12×52=522,
……
由此可得:MnNn=52n-1,
∴M1N1+M2N2+⋯+M2023N2023=5+52+522+⋯+522022=10×12+122+⋯+122023=10×1-122023=10-522022,
故选C.
32.B
【思路点拨】
设BC=x,则AC=2BC=2x,求得AB=3x,设CE=y,当点E在线段BC之间时,得到AE=2x+y,BE=x-y,求得y=27x,进而即可求出CDCB;当点E在线段AC之间时,同理可求出与条件不符,故舍去;
【解题过程】
解:设BC=x,则AC=2BC=2x,
∴AB=3x.
∵AB=2DE,
∴DE=32x.
设CE=y,
当点E在线段BC之间时,如图,
∴AE=AC+CE=2x+y,BE=BC-CE=x-y,
∴AD=AE-DE=2x+y-32x=12x+y.
∵AD+ECBE=32,
∴12x+y+yx-y=32,
∴y=27x,
∴CD=DE-CE=32x-y=32x-27x=1714x,
∴CDCB=1714xx=1714;
当点E在线段AC之间时,如图,
∴AE=AC-CE=2x-y,
∴AD=AE-DE=2x-32x-y=12x-y,BE=x+y.
∵AD+ECBE=32,
∴12x-y+yx+y=32,
解得:y=-23x,不符合题意,舍;
综上可得CDCB=1714.
故选B.
33.B
【思路点拨】
根据点P的位置分类讨论,分别画出对应的图形,利用路程÷速度=时间即可得出结论.
【解题过程】
解:∵数轴上的点O和点A分别表示0和10
∴OA=10
∵B是线段OA的中点,
∴OB=AB=12OA=5
①当点P由点O向点A运动,且未到点B时,如下图所示,PB=2
此时点P运动的路程OP=OB-PB=3
∴点P运动的时间为3÷2=32s;
②当点P由点O向点A运动,且已过点B时,如下图所示,PB=2
此时点P运动的路程OP=OB+PB=7
∴点P运动的时间为7÷2=72s;
③当点P由点A向点O运动,且未到点B时,如下图所示,PB=2
此时点P运动的路程为OA+AP=OA+AB-PB=13
∴点P运动的时间为13÷2=132s;
④当点P由点A向点O运动,且已过点B时,如下图所示,PB=2
此时点P运动的路程为OA+AP=OA+AB+PB=17
∴点P运动的时间为17÷2=172s;
综上所述:当PB=2时,则运动时间t的值为32秒或72秒或132或172秒
故选B.
34.C
【思路点拨】
结合图形根据题意正确进行角的和差计算即可判断.
【解题过程】
解:①如图可得∠DBA=∠ABF=15°,所以BA平分∠DBF,①正确;
②当0°<∠CBE<45°时,设∠DBM=x,
∵BM平分∠DBA,
∴∠ABM=∠DBM=x,
∴∠ABE=60°-2x,∠EBC=45°-60°-2x=2x-15°,
∴∠EBN=x-7.5°,∠MBN=x+60°-2x+x-7.5°=52.5°
当45°<∠CBE<90°时,设∠DBM=x,
∵BM平分∠DBA,
∴∠ABM=∠DBM=x,
∴∠ABE=60°-2x,
∴∠EBC=2x-15°,∠MBE=60°-x
∴∠EBN=∠CBN=x-7.5°,
∴∠MBN=60°-x+x-7.5°=52.5°,故②正确;
③∠CBE=30°时BD⊥BC,∠CBE=45°时AB⊥DE,∠CBE=75°时DB⊥AB故③正确;
④当0°<∠CBE<45°时∠DBC+∠ABE=105°,当45°<∠CBE<90°时∠DBC+∠ABE>105°,故④错误;
综上所述,正确的结论为①②③;
故选:C.
35.B
【思路点拨】
由于B选项中的结论是CD=2CN,而CD=CN+ND,因此只要判断ND和CN是否相等即可,根据ND=MN,而MN>CN,因此得到ND>CN,由此得出B选项错误.
【解题过程】
解:以O为顶点的角有6×52=15个,
所以A选项正确;
∵MN=ND,
∴ND>CN,
∴CD=CN+ND>CN+CN,即CD>2CN,
所以B选项错误;
由中点定义可得:MB=12AB,NC=12CD,
∴MN=MB+CN-CB=12AB+12CD-CB=12AB+CD-CB,
∵AB+CD=AD+CB,
∴MN=12AD+CB-CB=12AD-CB,
所以C选项正确;
由角平分线的定义可得:∠AOC=2∠MOC,∠BOD=2∠BON,
∵∠AOD=∠AOC+∠COB+∠DOB=5∠COB,
∴2∠MOC+2∠BON+∠BOC=5∠BOC,
∴∠MOC+∠BON=2∠BOC,
∴∠MON=∠MOC+∠COB+∠BON=2∠COB+∠COB=3∠COB
32∠MOC+∠BON=32×2∠COB=3∠COB,
∴∠MON=32∠MOC+∠BON,
所以D选项正确,
所以不正确的只有B,
故选:B.
36.D
【思路点拨】
分四种情况讨论:当OM1平分∠MOD时,当OD平分∠M1ON时,当OM1平分∠MON时,当OM1平分∠DON时,再列方程求解即可.
【解题过程】
解:∵∠DON=70°,
∴∠MOD=180°-70°=110°,
∵∠MOM1=5t,
∴当OM1平分∠MOD时,
∴∠MOM1=∠DOM1,
∴5t=110-5t,
解得:t=11,
当OD平分∠M1ON时,
∴∠M1OD=∠DON,
∴110-5t=70,
解得:t=8,
当OM1平分∠MON时,
∴5t=90,
解得:t=18,
当OM1平分∠DON时,
∴5t-110=12×70,
解得:t=29.
综上:t的值为:11,8,18,29;
故选D.
37.C
【思路点拨】
分四种情况,分别计算,即可求解.
【解题过程】
解:如图:射线OP是∠MON∠MOP=2∠NOP的三等分线,射线OQ是∠MOP∠QOP=2∠MOQ的三等分线,
则∠QOP=2x,∠NOP=12∠MOP=12×x+2x=32x,
∴∠MON=∠MOQ+∠QOP+∠NOP=x+2x+32x=92x;
如图:射线OP是∠MON∠MOP=2∠NOP的三等分线,射线OQ是∠MOP∠MOQ=2∠QOP的三等分线,
则∠QOP=12x,∠NOP=12∠MOP=12×x+12x=34x,
∴∠MON=∠MOQ+∠QOP+∠NOP=x+12x+34x=94x;
如图:射线OP是∠MON∠NOP=2∠MOP的三等分线,射线OQ是∠MOP∠MOQ=2∠QOP的三等分线,
则∠QOP=12x,∠NOP=2∠MOP=2×x+12x=3x,
∴∠MON=∠MOQ+∠QOP+∠NOP=x+12x+3x=92x;
如图:射线OP是∠MON∠NOP=2∠MOP的三等分线,射线OQ是∠MOP∠QOP=2∠MOQ的三等分线,
则∠QOP=2x,∠NOP=2∠MOP=2×x+2x=6x,
∴∠MON=∠MOQ+∠QOP+∠NOP=x+2x+6x=9x;
综上,∠MON为94x或92x或9x,
故选:C.
38.C
【思路点拨】
由∠AOB=∠COD=90°根据等角的余角相等得到∠AOC=∠BOD,而∠COE=∠BOE,即可判断①正确;由∠AOD+∠COB=∠AOD+∠AOC+90°,而∠AOD+∠AOC=90°,即可判断②正确;由∠COB-∠AOD=∠AOC+90°-∠AOD,而不能判断∠AOC≠∠AOD,即可判断③错误;根据∠AOE=∠DOE,可得∠AOF=∠DOF,从而得到∠AOD=2∠DOF,设∠AOF=∠DOF=x,则∠AOD=2x,可得∠AOC=∠BOD=90°-2x,再由∠FOD:∠EOC=1:6,可得∠COE=∠BOE=6x,再由∠AOF+∠AOC+∠COE=180°,求出x,可得∠DOF=18°,故④错误,即可.
【解题过程】
解:∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
∵∠COE=∠BOE,
∴∠COE+∠AOC=∠BOD+∠BOE,
∴∠AOE=∠DOE,故①正确;
∵∠BOC=∠AOC+∠AOB=∠AOC+90°,
∴∠AOD+∠COB=∠AOD+∠AOC+90°=90°+90°=180°,故②正确;
∴∠COB-∠AOD=∠AOC+90°-∠AOD,
根据题意无法确定∠AOC与∠AOD的大小关系,
∴∠COB-∠AOD=90°不一定成立,故③错误;
∵∠AOE=∠DOE,E、O、F三点共线,
∴∠AOF=∠DOF,
∴∠AOD=2∠DOF,
设∠AOF=∠DOF=x,则∠AOD=2x,
∴∠AOC=∠BOD=90°-2x,
∵∠FOD:∠EOC=1:6,
∴∠COE=∠BOE=6x,
∵∠AOF+∠AOC+∠COE=180°,
∴x+90°-2x+6x=180°,
解得:x=18°,
即∠DOF=18°,故④错误.
所以,正确的结论有2个.
故选:C.
39.B
【思路点拨】
(1)根据角平分线的意义来分析射线OM的速度;(2)先假定时间为15秒,然后来分析A、C的位置的变化情况;(3)根据角平分线的性质来求即可;(4)用120°除以2即可判断.
【解题过程】
解:(1)∵∠BOC以每秒2°的速度旋转,
∴角平分线OM的旋转速度为每秒1°,
故(1)是错误的;
(2)设转了t秒,∠AOB=2t°,
则∠BON=12(150-2t)°,
∠AON=∠BON+∠AOB=(75+t)°,
当t=15秒时,∠AON=90°,
故(2)正确;
(3)∵∠AOD=150°,∠BOC=30°,
设∠DON=x°,∠AOM=y°,则2x+2y-30=150,
∴x+y=90;
∴∠MON=x+y-30=60,即∠MON=60°,
故(3)是正确的;
(4)∵120°÷2=60秒,
∴在整个过程中∠BOC在∠MON内部持续时长为45秒,
故(4)错误.
∴正确的是(2)(3),
故选:B.
40.B
【思路点拨】
由角平分线的定义可求解∠AOD=∠BOD=60°-∠BOE,易求∠EOC=3∠BOE,结合平角的定义可求解∠BOD的度数,判定①;结合∠DOE=60°可求解∠AOE的度数,进而可判定②;结合余角的定义可判定③;利用补角的定义可判定④
【解题过程】
解:∵OD平分∠AOB,∠DOE=60°,
∴∠AOD=∠BOD=60°-∠BOE,
∵∠BOE=13∠EOC,
∴∠EOC=3∠BOE,
∵AC是一条直线,
∴∠AOD+∠BOD+∠BOE+∠EOC=180°,
∴60°-∠BOE+60°-∠BOE+∠BOE+3∠BOE=180°,
∴∠BOE=30°,
∴∠BOD=30°,故①错误;
∵∠BOD=∠AOD=30°,
∴∠AOE=∠AOD+∠BOD+∠BOE=30°+30°+30°=90°,
∴∠EOC=180°-∠AOE=90°,
∴∠AOE=∠EOC,
∴射线OE平分∠AOC,故②正确;
∵∠BOE=30°,∠AOB=60°,∠DOE=60°,
∴∠AOB+∠BOE=90°,∠BOE+∠DOE=90°,
∴图中与∠BOE互余的角有2个,故③正确;
∵∠AOE=∠EOC=90°,
∴∠AOE+∠EOC=180°,
∵∠EOC=90°,∠DOB=30°,∠BOE=30°,∠AOD=30°,
∴∠COD+∠AOD=180°,∠COD+∠BOD=180°,∠COD+∠BOE=180°,∠COB+∠AOB=180°,∠COB+∠DOE=180°,
∴图中互补的角有6对,故④正确,
正确的有②③④,故选:B.
专题13.3 期末复习填空压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版): 这是一份专题13.3 期末复习填空压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版),文件包含专题133期末复习填空压轴题专项训练压轴题专项训练苏科版原卷版docx、专题133期末复习填空压轴题专项训练压轴题专项训练苏科版解析版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
专题13.2 期末复习选择压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版): 这是一份专题13.2 期末复习选择压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版),文件包含专题132期末复习选择压轴题专项训练压轴题专项训练苏科版原卷版docx、专题132期末复习选择压轴题专项训练压轴题专项训练苏科版解析版docx等2份试卷配套教学资源,其中试卷共58页, 欢迎下载使用。
专题13.1 期末复习解答压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版): 这是一份专题13.1 期末复习解答压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版),文件包含专题131期末复习解答压轴题专项训练压轴题专项训练苏科版原卷版docx、专题131期末复习解答压轴题专项训练压轴题专项训练苏科版解析版docx等2份试卷配套教学资源,其中试卷共78页, 欢迎下载使用。












