2023年潍坊市初中学业水平考试数学一模预测卷(1)

这是一份2023年潍坊市初中学业水平考试数学一模预测卷(1)，共6页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、单项选择题(本大题共8小题，每小题4分，共32分.每小题四个选项中只有一项正确，请把正确的选出来，选对得4分，错选、不选或选出的答案超过一个均记0分)
1. D 2. D 3. B 4. A 5. B 6. C 7. C 8. D
二、多项选择题(本大题共4 小题，每小题5 分，共20分.每小题的四个选项中，有多项正确，全部选对得 5分，部分选对得3分，有错选的得0分)
9. AC 10. BD 11. ACD 12. ABD
三、填空题(本大题共4 小题，每小题5 分，共20 分.只写最后结果)
13. -1 14.π- 3 15.(0, 3²⁰²¹) 16.1+ 3
四、解答题(本大题共7 小题，共 78 分.请写出必要的文字说明、证明过程或演算步骤)
17.解:(1)7676⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
(2)100060⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分
(3)根据题意画树状图如下：
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 8分
由树状图，得共有 9 种等可能的结果，其中他俩第二次同时选课程 A 或课程 B 的结果有 2 种，
则他俩第二次同时选课程 A 或课程 B的概率是 29.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 10分
18.解:如图,过 C作CE⊥AB 于 E,过D作 DF⊥AB交AB 的延长线于 F,则CE∥DF.
∵AB∥CD,
∴四边形 CDFE 是矩形.
∴EF=CD=120m,DF=CE.⋯⋯⋯⋯⋯⋯⋯2分
在 Rt△BDF中,∵∠BDF=32°,BD=80m,
∴DF=BD⋅cs32∘≈80×1720=68m, BF=BD⋅sin32∘≈80×1732=852m.⋯⋯⋯3分
∴BE=EF−BF=1552m,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
在 Rt△ACE中,∵∠ACE=42°,CE=DF=68m,
∴AE=CE⋅tan42∘≈68×910=3065m,……8分您看到的资料都源自我们平台，20多万份试卷，家威杏 MXSJ663 每日最新，性比价最高 ∴AB=AE+BE=1552+3065≈139m.
答:木栈道AB的长度约为139m.⋯⋯⋯10分
19.(1)解:举反例:<0.6>+<0.7>=1+1=2,而<0.6+0.7>=<1.3>=1,
∴<0.6>+<0.7>≠<0.6+0.7>.
∴+=不一定成立. 2分
(2)解:∵=5,
∴4.5≤x+2<5.5.
∴2.5≤x<3.5. 4分
(3)证明:设=n,则 n−12≤x ∴n+m−12≤x+m∴=n+m=+m.⋯⋯⋯⋯⋯7分
(4)解: ∵x≥0,43x为整数，
∴设 43x=k,k为整数，则 x=34k.
∴<34k>=k.∴k−12≤34k∴k=0,1,2. ∴x=0, 34，32 .……………………… 10分
20.解:(1)62 10340⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
(2)由题意,得
ω=(60+2x)(500-10x)-40x-500×40
=−20x²+360x+10000.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分
3w=20x²+360x+10000 =−20x−9²+11620.…………………………8分
∵0≤x≤8,x为整数,
当x≤9时，w 随x的增大而增大，
∴当x=8时,w取最大值, w加水=11600.
答：批发商经营这批水果所能获得的最大利润为11600元…………………………12分
21.(1)证明:如图,连接OC.
∵OA=OC,∴∠DAC=∠ACO.
∵∠DCB=∠DAC,∴∠DCB=∠ACO.⋯1分
∵AB为⊙O的直径,
∴∠BCO+∠ACO=∠ACB=90°.⋯⋯⋯⋯⋯2分
∴∠BCO+∠DCB=90°,即∠OCD=90°.
∴OC⊥CD.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
∵OC是⊙O的半径,
∴CD是⊙O的切线⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
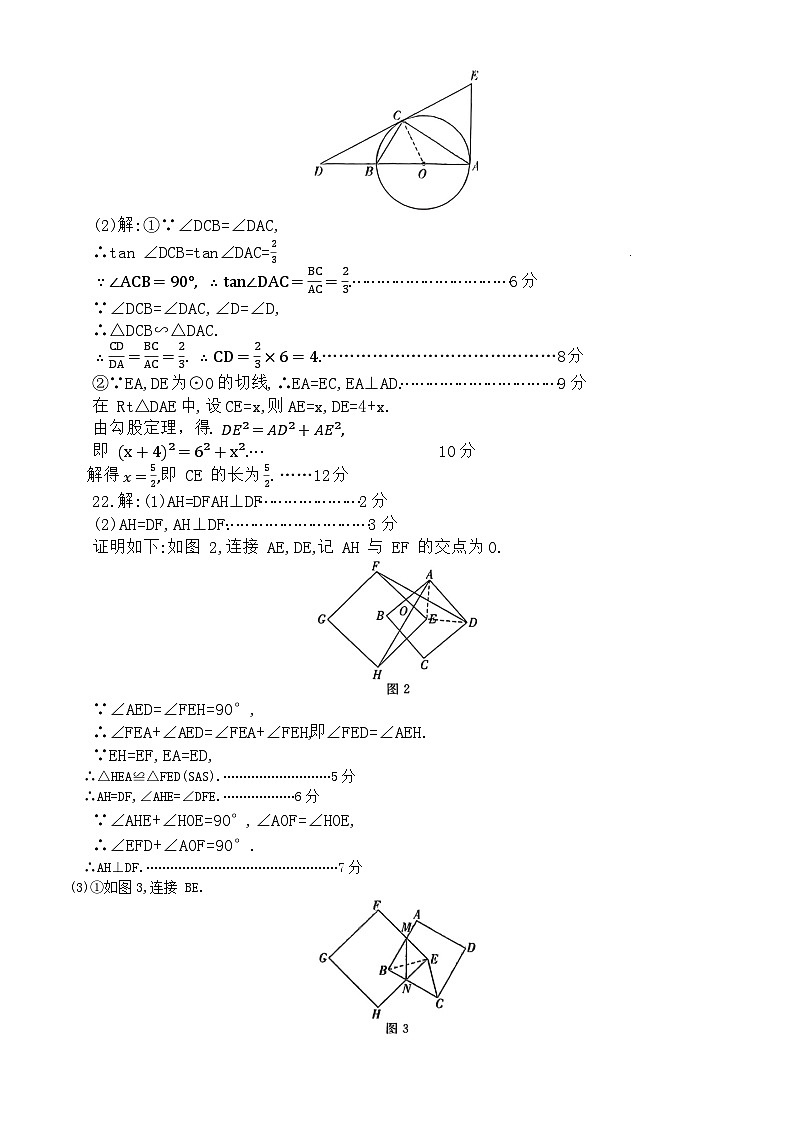
(2)解:①∵∠DCB=∠DAC,
∴tan ∠DCB=tan∠DAC= 23.
∵∠ACB=90°, ∴tan∠DAC=BCAC=23.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分
∵∠DCB=∠DAC,∠D=∠D,
∴△DCB∽△DAC.
∴CDDA=BCAC=23. ∴CD=23×6=4.……………………………………8分
②∵EA,DE为⊙O的切线,∴EA=EC,EA⊥AD.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9分
在 Rt△DAE中,设CE=x,则AE=x,DE=4+x.
由勾股定理，得. DE²=AD²+AE²,
即 x+4²=6²+x².⋯ 10分
解得 x=52,即 CE 的长为 52.……12分
22.解:(1)AH=DFAH⊥DF⋯⋯⋯⋯⋯⋯⋯2分
(2)AH=DF,AH⊥DF.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
证明如下:如图 2,连接 AE,DE,记 AH 与 EF 的交点为O.
∵∠AED=∠FEH=90°,
∴∠FEA+∠AED=∠FEA+∠FEH,即∠FED=∠AEH.
∵EH=EF,EA=ED,
∴△HEA≌△FED(SAS).⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
∴AH=DF,∠AHE=∠DFE.⋯⋯⋯⋯⋯⋯6分
∵∠AHE+∠HOE=90°,∠AOF=∠HOE,
∴∠EFD+∠AOF=90°.
∴AH⊥DF.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7分
(3)①如图3,连接 BE.
∵四边形 ABCD 是正方形,
∴BE=CE,∠MBE=∠NCE=45°,∠BEC=90°.
∵四边形 EFGH 是正方形,
∴∠FEH=90°.
∴∠MEB+∠BEN=∠NEC+∠BEN.
∴∠MEB=∠NEC.
∴△MBE≌△NCE(ASA).
∴BM=CN.
∵AM=2,AB=6,
∴BM=CN=4,BN=2.
∴SBMN+SCEN=12BN⋅BM+12CN⋅12AB= 12×2×4+12×4×3=10.………………………10分
②若α=45°,如图4,四边形 BMEN 是正方形;四边形 NMEC 是平行四边形;四边形 NMAE 是平行四边形.(答案不唯一)⋯⋯⋯⋯⋯⋯⋯⋯⋯12分
23.解:(1)把 A(-2,0),B(4,0)两点分别代入抛物线 y=ax²−x+c中，得 4a+2+c=0,16a−4+c=0.
解得 a=12,c=−4.
∴该抛物线的解析式为 y=12x2−x−4.⋯2分
(2)如图1,连接 PC,过点 P 作 PE∥y轴,交 BC于点 E.
∵BDCD=12,∴SBDP=13SCPB.易知点C 的坐标为(0,-4).
设直线 BC的解析式为y=kx+b,
∴4k+b=0,b=−4.解得 k=1，b=−4.
∴直线BC的解析式为y=x-4.⋯⋯⋯⋯⋯3分
设E(t,t-4),则 Pt12t2−t−4.
∴EP=t−4−12t2−t−4=−12t2+2t=−12t−22+2.∴当t=2时，PE的长度最大，且最大值是2.
… …… ……………………5分
∵SCPB=12PE⋅OB=12PE⋅4,∴S△CPB的最大值 =12×2×4=4.
∴△BDP 面积最大值为 43 .………………6分
(3)∵B(4,0),C(0,-4),BD= 12, ∴D83−43.
抛物线的对称轴是直线 x=1.
分三种情况：
①如图2，四边形ADNM是平行四边形，
∵A−20,D83−43,点 M 的横坐标为1，
∴点 N 的横坐标为 83+1−−2=173.当 x=173时. y=12×1732−173−4=11518, ∴N17311518. 8分
②如图3，四边形ADMN 是平行四边形，
由平移，得点 N 的横坐标是 −113,当 x=−113时, y=12×−1132+113−4=11518, ∴N−11311518. ………………10分
③如图4，四边形 ANDM是平行四边形，
由平移，得点 N 的横坐标为 −13,
当 x=−13时, y=12×−132+13−4=−6518, ∴N−13−6518.
综上所述，点 N的坐标为 17311518或 −11311518或 −13−6518.…………………………………………12分