

2024届中考数学高频考点专项练习:专题九 一次函数综合训练(B)及答案
展开A.B.C.D.无法确定
2.如图,两摞规格完全相同的作业本整齐地叠放在桌面上,根据图中所给出的数据信息,甲、乙、丙、丁四人分别给出下列信息:
甲:每本作业本的厚度为3mm
乙:桌面距离地面的高度为860mm
丙:若有一摞这种规格作业本x本整齐放在桌面上,这摞作业本顶部距离地面高度为h(单位:mm),则
丁:若把270本这种规格的作业本整齐的摆成一摆放在桌面上,则这摞作业本顶部距离地面的高度h为
对于四个信息,下列说法正确的是( )
A.只有甲错误B.只有乙、丙正确
C.只有甲、丙正确D.都正确
3.如图,在平面直角坐标系中,已知是以点A为直角顶点的等腰直角三角形,点B在y轴正半轴上,点,将沿x轴正方向平移得到,若点E恰好落在直线上,则此时点D的坐标为( )
A.B.C.D.
4.对于一次函数,下列结论正确的是( )
A.函数的图象不经过第三象限
B.函数的图象与x轴的交点坐标是
C.函数的图象向下平移4个单位长度后得到的图象
D.若两点,在该函数图象上,则
5.已知直线与x轴、y轴分别交于A、B两点,点P是第一象限内的点,若为等腰直角三角形,则点P的坐标为( )
A.B.或
C.或或D.或或或
6.如图,已知直线与x轴、y轴分别交于点A和点B,M是OB上一点,若将沿AM折叠,点B恰好落在x轴上的点处,则直线AM所对应的函数解析式是( )
A.B.C.D.
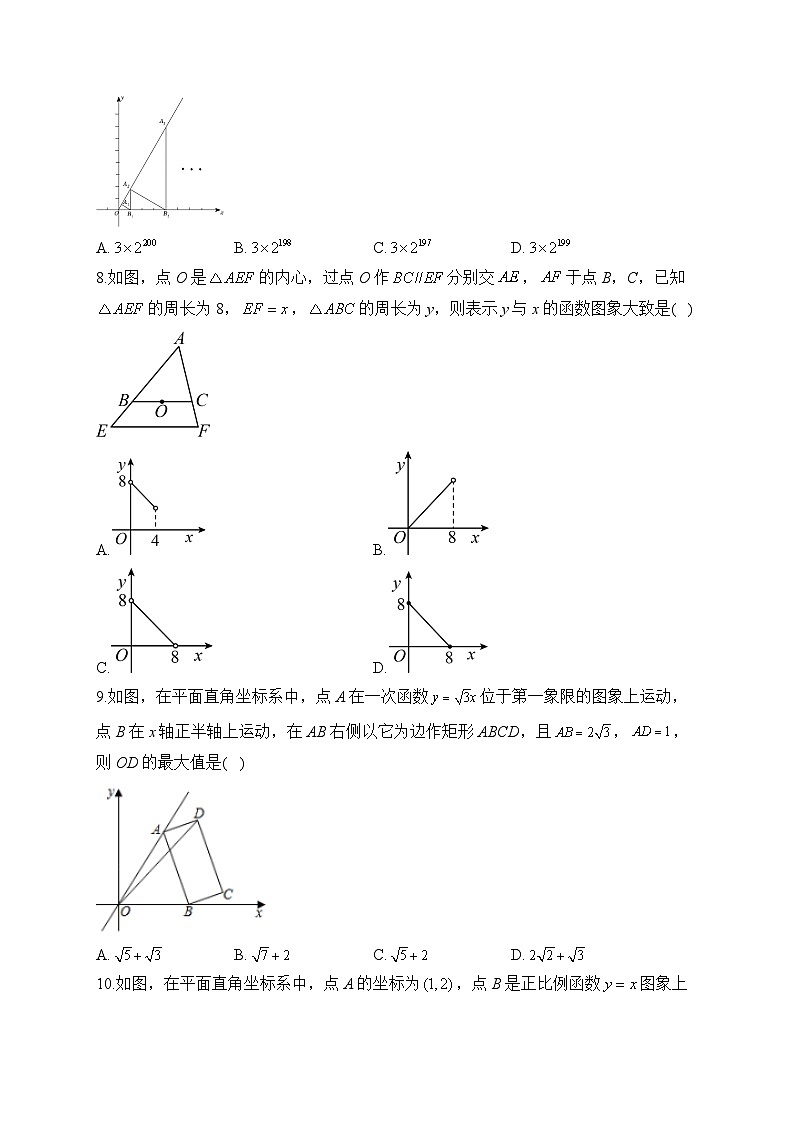
7.如图,过直线上的点作,交x轴于点,过点作轴,交直线l于点;过点作交x轴于点,过点作轴,交直线l于点;按照此方法继续作下去,若,则线段的长度为( )
A.B.C.D.
8.如图,点O是的内心,过点O作分别交,于点B,C,已知的周长为8,,的周长为y,则表示y与x的函数图象大致是( )
A.B.
C.D.
9.如图,在平面直角坐标系中,点A在一次函数位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且,,则OD的最大值是( )
A.B.C.D.
10.如图,在平面直角坐标系中,点A的坐标为,点B是正比例函数图象上一动点,点C是y轴上一动点,则周长的最小值为_________.
11.如图,在平面直角坐标系xOy中,已知点,,C为平面内的动点,且满足,D为直线上的动点,则线段CD长的最小值为________.
12.如图, 点A,B 的坐标分别为,, 点C 为坐标平面内一点, , 点 M为线段AC 的中点, 连接OM, 当OM 取最大值时, 点M 的坐标为__________.
13.规定;两个函数,的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数与的图象关于y轴对称则这两个函数互为“Y函数”.若函数(k为常数)的“Y函数“图象与x轴只有一个交点,则其“Y函数“的解析式为_______________.
14.近年来,四川天府新区取得了飞速的发展,以成都科学城发展为例,兴隆湖畔集结了一大批领先的科技创新领军项目,正如火如荼地推进建设,据报道,新区某公司打算购买A,B两种花装点城区道路,公司负责人到花卉基地调查发现:购买1盆A种花和2盆B种花需要14元,购买2盆A种花和1盆B种花需要13元.
(1)求A,B两种花单价各为多少元?
(2)公司若购买A,B两种花共10000盆,设购买的A种花m盆(),总费用为W元;
①求W与m的关系式;
②请你帮公司设计一种购花方案,使总花费最少?并求出最少费用为多少元?
15.如图,在平面直角坐标系中,直线与x轴交于点B,与y轴交于点A,,,直线交直线于点C.
(1)求直线的解析式及C点的坐标;
(2)如图1,P为直线上一动点且在第一象限内,M、Q为x轴上动点,Q在M右侧且,当时,求最小值;
(3)如图2,将沿着射线方向平移,平移后A、O、B三点分别对应D、E、F三点,直线上是否存在N点,使得为等腰直角三角形,若存在,请直接写出N点坐标;若不存在,请说明理由.
答案以及解析
1.答案:A
解析:,
y随x的增大而减小,
又点,在一次函数的图象上,且,
.
故选:A.
2.答案:A
解析:, 故甲的描述错误;
桌面距离地面的高度为,故乙的描述正确;
有一摞这种规格作业本x本整齐放在桌面上,这摞作业本顶部距离地面高度为h(单位:mm),则;故丙的描述正确;
当时,,
把270本作业本整齐地叠成一摞摆放在桌面上,用科学记数法表示h为.
故丁的描述正确;
故选:A.
3.答案:B
解析:点,
,
是以点A为直角顶点的等腰直角三角形,
,
,
E是点B沿x轴向右平移得到的点,
点E的纵坐标为2,
将代入中,得,
点,
点E是点B向右平移4个单位长度得到的,
点D也是点A向右平移4个单位长度得到的,
点,即点,
故选:B.
4.答案:A
解析:因为,,所以函数的图象经过第一、二、四象限,不经过第三象限,故A选项正确;当时,,解得,故函数的图象与x轴的交点坐标是,故B选项错误;一次函数的图象向下平移4个单位长度后得到的图象,故C选项错误;若两点,在该函数图象上,,则,故D选项错误.故选A.
5.答案:C
解析:解:直线与x轴、y轴分别交于A、B两点,当时,,当时,;故A、B两点坐标分别为,,点P是第一象限内的点且为等腰直角三角形,
①当时,P点坐标为;
②当时,P点坐标为;
③当时,P点坐标为.
6.答案:C
解析:在中,令得,令得,
点A的坐标为,点B的坐标为,
,
由折叠的性质,得,
,
设,则,
在中,,即,
解得,
设直线AM所对应的函数解析式为,
将代入,得,
解得.
直线AM所对应的函数解析式为.
故选C.
7.答案:C
解析:直线,
直线l与x轴夹角为,
为x轴上一点,且,
,,
,
,
,
,
,
,
,
,
故选:C.
8.答案:A
解析:如图所示,连接,,
点O是的内心,
,,
,
,,
,,
,,
的周长,
的周长为8,,
,
,
,
,
,
y与x的函数关系式为:.
故选:A.
9.答案:B
解析:点A在一次函数的图象上,,作的外接圆,连接OP,PA,PB,PD,作,交AB于H,垂足为G,如图所示,四边形ABCD是矩形,,,四边形AHGD是矩形,,,,,,,,,,,.,OD的最大值为.
10.答案:
解析:作A点关于直线的对称点P,关于y轴的对称点Q,连接PQ交直线于B,交y轴于C,如图.
因为,,所以.
因为P,B,C,Q四点共线,
所以此时周长最小,最小值为PQ的长度.
由知,,
所以,
则周长的最小值为,
故答案为.
11.答案:
解析:取AB的中点E,过点E作直线的垂线,垂足为D,
点,,
,,
,
,
,
点C在以AB为直径的圆上,
线段CD长的最小值为.
故答案为:.
12.答案:
解析:,,
点 C在以点B 为圆心 2 为半径的 上,
如图. 连接AB, 取AB 的中点D, 连接DM, 则 DM是 的中位线,
,点 M在以点D 为圆心 1 为半径 的 上,
连接OD, 则 ,
当 O,D,M三 点共线时, OM取得最大值 (此时点M 用点 表示).
,,, 点 在直线 上,.
设, 则 ,,
当OM 取最大值时, 点M 的 坐标为.
13.答案:或
解析:函数(k为常数)的“Y函数”图象与x轴只有一个交点,
函数(k为常数)的图象与x轴也只有一个交点,
当时,函数解析为,它的“Y函数”解析式为,它们的图象与x轴只有一个交点,
当时,此函数是二次函数,
它们的图象与x轴都只有一个交点,
它们的顶点分别在x轴上,
,得,
故,解得,
故原函数的解析式为,
故它的“Y函数”解析式为,
故答案为:或.
14.答案:(1)A种花的单价为4元,B种花的单价为5元
(2)当购买A种花5000盆、B种花5000盆时,总花费最少,最少费用为45000元
解析:(1)设A种花的单价为a元,B种花的单价为b元,
,
解得:,
即A种花的单价为4元,B种花的单价为5元;
(2)①由题意可得,
,
即W与m的关系式是;
②,
W随m的增大而减小,
,
当时,W取得最小值,此时,,
即当购买A种花5000盆、B种花5000盆时,总花费最少,最少费用为45000元.
15.答案:(1),
(2)
(3)存在,或或
解析:(1),
点A的坐标是,
,
,
点B的坐标为,
设直线的解析式为,
把点A和点B的坐标代入可得,
解得,
直线的解析式为,
联立直线和直线的解析式得,
解得,
点C的坐标是;
(2),,
,
,
,,
直线交直线于点C.
,
,
,
点P在点C的上方,
P为直线上一动点且在第一象限内,
设点P的坐标为,其中,
点P到x轴的距离为,
,
,
解得,
,
点P的坐标是,
如图,过点P向左作轴,且,
则的坐标为,再作点关于x轴的对称点,
则的坐标为,
则连接交x轴于点M,在x轴上截取,连接,
由作图过程知四边形是平行四边形,则,
的最小值为,
作于点,则的坐标,则,,
的最小值为.
即最小值为;
(3)存在,理由如下:
将沿着射线方向平移,即将向左平移n个单位,向下平移个单位,
,,
①当时,如图,
直线的解析式为,
,
,
为等腰直角三角形,
,
,
,
N点坐标为;
②当时,如图,
直线的解析式为,
,
,
为等腰直角三角形,
,
,
,
N点坐标为;
③当时,如图,过点N作于H,
为等腰直角三角形,
,,
,,
点N的横坐标为,
直线的解析式为,
,
,
,
N点坐标为;
综上所述,N点坐标为或或.
2024届中考数学高频考点专项练习:专题三 分式综合训练(B)及答案: 这是一份2024届中考数学高频考点专项练习:专题三 分式综合训练(B)及答案,共9页。试卷主要包含了代数式的家中来了几位客人,已知,则,下列关于分式的判断中错误的是,已知,则的值是,题目,已知a,b为实数且满足,,设,等内容,欢迎下载使用。
2023届中考数学高频考点专项练习:专题十五 圆综合训练(B): 这是一份2023届中考数学高频考点专项练习:专题十五 圆综合训练(B),共13页。
2023届中考数学高频考点专项练习:专题九 一次函数综合训练(B): 这是一份2023届中考数学高频考点专项练习:专题九 一次函数综合训练(B),共13页。试卷主要包含了对于实数,定义符号,其意义等内容,欢迎下载使用。












