人教版七年级数学上册同步压轴题期末考试压轴题训练1(学生版+解析)

这是一份人教版七年级数学上册同步压轴题期末考试压轴题训练1(学生版+解析)，共19页。试卷主要包含了计算的结果是等内容，欢迎下载使用。

A．15°B．75°C．15°或75°D．不能确定
2．2018年电影《我不是药神》反映了进口药用药贵的事实，从而引起了社会的广泛关注.国家针对部分药品进行改革，看病贵将成为历史.某药厂对售价为m元的药品进行了降价，现在有三种方案.
方案一：第一次降价10%，第二次降价30%；
方案二：第一次降价20%，第二次降价15%；
方案三：第一、二次降价均为20%.三种方案哪种降价最多( )
A．方案一B．方案二C．方案三D．不能确定
3．如图，甲､乙两动点分别从正方形ABCD的顶点A，C同时沿正方形的边开始移动，甲按顺时针方向环形，乙按逆时针方向环行，若乙的速度是甲的3倍，那么它们第一次相遇在AD边上，请问它们第2019次相遇在哪条边上?( )
A．ADB．DCC．BCD．AB
4．观察下列一组图形，第①个图形有3个小圆圈，第②个图形有5个小圆圈，第③个图形有9个小圆圈，第④个图形有15个小圆圈，…，按此规律排列下去，第9个图形中小圆圈的个数为( )
A．59B．75C．81D．93
5．计算的结果是( )
A．B．C．D．
6．若，，且的绝对值与相反数相等，则的值是( )
A．B．C．或D．2或6
7．若多项式(m为常数)不含项，则____________．
8．已知，，都是不等于0的有理数，且的最大值是，最小值是，则______．
9．如图，在数轴上，点表示1，现将点沿数轴做如下移动：第一次将点向左移动3个单位长度到达点，第2次将点向右平移6个单位长度到达点，第3次将点向左移动9个单位长度到达点…，则第2020次移动到点时，在数轴上对应的实数是_________．
10．如图，数轴上的O点为原点，A点表示的数为，动点P从O点出发，按以下规律跳动：第1次从O点跳动到OA的中点处，第2次从点跳动到的中点处，第3次从点跳动到的中点处，…，第n次从点跳动到的中点处，按照这样的规律继续跳动到点，，，…，(，n是整数)处，那么点所表示的数为_________．
11．已知关于x的方程的解为正整数，则整数k的值为_________．
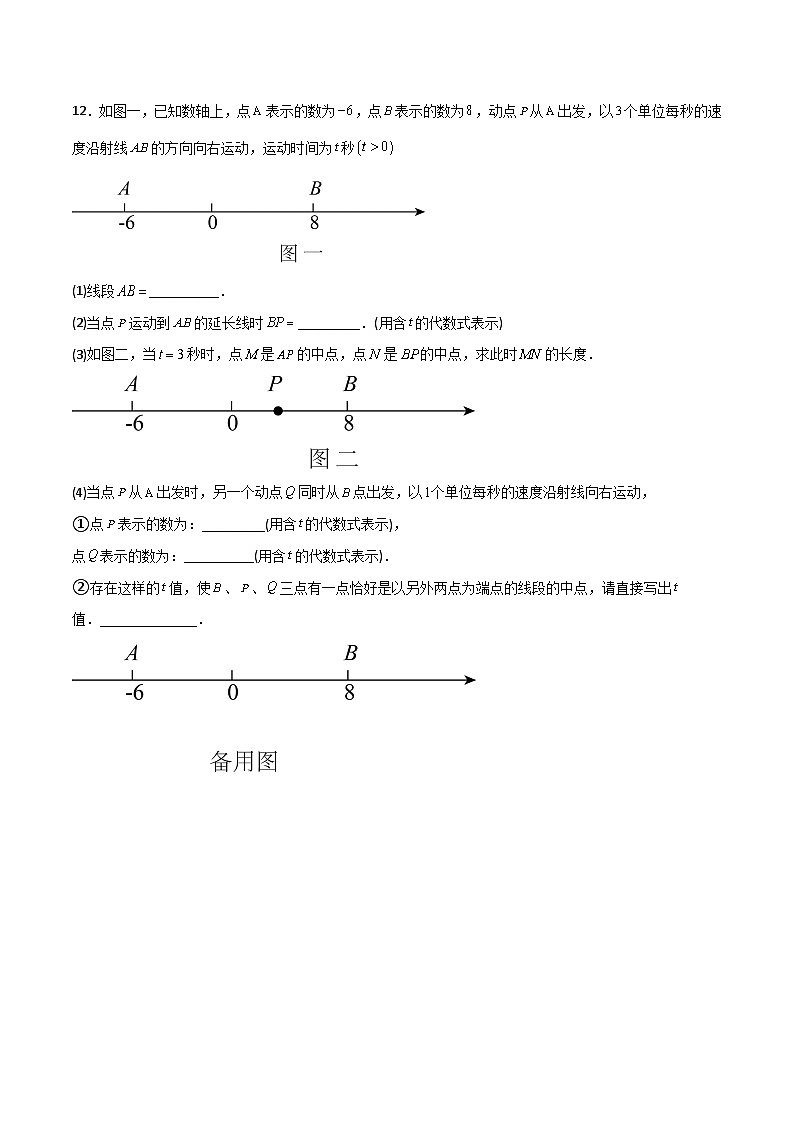
12．如图一，已知数轴上，点表示的数为，点表示的数为，动点从出发，以个单位每秒的速度沿射线的方向向右运动，运动时间为秒
(1)线段__________．
(2)当点运动到的延长线时_________．(用含的代数式表示)
(3)如图二，当秒时，点是的中点，点是的中点，求此时的长度．
(4)当点从出发时，另一个动点同时从点出发，以个单位每秒的速度沿射线向右运动，
①点表示的数为：_________(用含的代数式表示)，
点表示的数为：__________(用含的代数式表示)．
②存在这样的值，使、、三点有一点恰好是以另外两点为端点的线段的中点，请直接写出值．______________．
13．数学课上李老师说：咱们一起来玩儿一个找原点的游戏吧！
(1)如图1，在数轴上标有A，B两点，已知A，B两点所表示的数互为相反数．
①如果点A所表示的数是，那么点B所表示的数是_______；
②在图1中标出原点O的位置；
(2)图2是小敏所画的数轴，数轴上标出的点中任意相邻两点间的距离都相等．
根据小敏提供的信息，标出隐藏的原点O的位置，并写出此时点C所表示的数是____________；
(3)如图3，数轴上标出若干个点，其中点A，B，C所表示的数分别为a，b，c．若数轴上标出的若干个点中每相邻两点相距1个单位(如AB=1)，且．
①试求a的值；
②若点D也在这条数轴上，且CD=2，求出点D所表示的数．
14．已知∠AOB=120°，∠COD=60°．
(1)如图1，当∠COD在∠AOB的内部时，若∠AOD=95°，求∠BOC的度数；
(2)如图2，当射线OC在∠AOB的内部，OD在∠AOB的外部时，试探索∠AOD与∠BOC的数量关系，并说明理由；
(3)如图3，当∠COD在∠AOB的外部时，分别在∠AOC内部和∠BOD内部画射线OE，OF，使∠AOE =∠AOC，∠DOF=∠BOD，求∠EOF的度数．
15．如图所示，已知直角三角板和直角三角板，，．将两块三角板摆放在一起，且点重合．过点作射线、，且，．
(1)按图1所示位置摆放，则______；
(2)按图2所示位置摆放，求的值；
(3)按图3所示位置摆放，且，求的值．
期末考试压轴题训练(一)
1．已知∠AOB=30°，∠BOC=45°，则∠AOC等于( )
A．15°B．75°C．15°或75°D．不能确定
【答案】C
【详解】如图：
当∠AOB在∠BOC的内部时，∠AOC=∠BOC–∠AOB=45°–30°=15°；
当∠AOB在∠BOC的外部时，∠AOC=∠BOC+∠AOB=45°+30°=75°.故选C．
2．2018年电影《我不是药神》反映了进口药用药贵的事实，从而引起了社会的广泛关注.国家针对部分药品进行改革，看病贵将成为历史.某药厂对售价为m元的药品进行了降价，现在有三种方案.
方案一：第一次降价10%，第二次降价30%；
方案二：第一次降价20%，第二次降价15%；
方案三：第一、二次降价均为20%.三种方案哪种降价最多( )
A．方案一B．方案二C．方案三D．不能确定
【答案】A
【详解】解：由题意可得：方案一降价0.1m+m(1-10%)30%=0.37m；
方案二降价0.2m+m(1-20%)15%=0.32m； 方案三降价0.2m+m(1-20%)20%=0.36m；
故答案为A.
3．如图，甲､乙两动点分别从正方形ABCD的顶点A，C同时沿正方形的边开始移动，甲按顺时针方向环形，乙按逆时针方向环行，若乙的速度是甲的3倍，那么它们第一次相遇在AD边上，请问它们第2019次相遇在哪条边上?( )
A．ADB．DCC．BCD．AB
【答案】C
【详解】解：设正方形的边长为a，因为乙的速度是甲的速度的3倍，时间相同，甲乙所行的路程比为，把正方形的每一条边平均分成2份，由题意知：
①第一次相遇甲乙行的路程和为2a，乙行的路程为，甲行的路程为，在AD边的中点相遇；
②第二次相遇甲乙行的路程和为4a，乙行的路程为，甲行的路程为，在CD边的中点相遇；
③第三次相遇甲乙行的路程和为4a，乙行的路程为，甲行的路程为，在BC边的中点相遇；
④第四次相遇甲乙行的路程和为4a，乙行的路程为，甲行的路程为，在AB边的中点相遇；
⑤第五次相遇甲乙行的路程和为4a，乙行的路程为，甲行的路程为，在AD边的中点相遇；
……
四次一个循环，因为，所以它们第2019次相遇在边BC中点上．
故选择C．
4．观察下列一组图形，第①个图形有3个小圆圈，第②个图形有5个小圆圈，第③个图形有9个小圆圈，第④个图形有15个小圆圈，…，按此规律排列下去，第9个图形中小圆圈的个数为( )
A．59B．75C．81D．93
【答案】B
【详解】解：根据第②个图形有3+1×2=5个小圆圈，第③个图形有3+2×3=9个小圆圈，第④个图形有3+3×4=15个小圆圈，…，按此规律排列下去，第9个图形中小圆圈的个数为3+8×9=75，
故选：B．
5．计算的结果是( )
A．B．C．D．
【答案】D
【详解】解：，
=
=，
=，
=，
故选：D．
6．若，，且的绝对值与相反数相等，则的值是( )
A．B．C．或D．2或6
【答案】C
【详解】解：∵，，
∴，，
∵的绝对值与相反数相等，
∴＜0，
∴，，
或，
故选：C．
7．若多项式(m为常数)不含项，则____________．
【答案】7
【详解】解：
=
∵多项式中不含xy项
∴7-m=0
∴m=7
故答案为：7．
8．已知，，都是不等于0的有理数，且的最大值是，最小值是，则______．
【答案】0
【详解】解：当a，b，c为正数时，有最大值是3,
∴m=3，
当a，b，c为负数时，的最小值是-3，
∴n=-3．
∴m+n=3-3=0．
故答案为：0．
9．如图，在数轴上，点表示1，现将点沿数轴做如下移动：第一次将点向左移动3个单位长度到达点，第2次将点向右平移6个单位长度到达点，第3次将点向左移动9个单位长度到达点…，则第2020次移动到点时，在数轴上对应的实数是_________．
【答案】3031
【详解】解：第一次点A向左移动3个单位长度至点A1，则A1表示的数，1-3=-2；
第2次从点A1向右移动6个单位长度至点A2，则A2表示的数为-2+6=4；
第3次从点A2向左移动9个单位长度至点A3，则A3表示的数为4-9=-5；
第4次从点A3向右移动12个单位长度至点A4，则A4表示的数为-5+12=7；
第5次从点A4向左移动15个单位长度至点A5，则A5表示的数为7-15=-8；
第6次从点A5向左移动18个单位长度至点A6，则A6表示的数为-8+18=10；
…；
发现序号是偶数的点在正半轴上，
A2：4，
A4：7=4+3×1，
A6：10=4+3×2，
A2n：4+3×(n-1)，
则点A2020表示：4+3×1009=3031，
故答案为：3031．
10．如图，数轴上的O点为原点，A点表示的数为，动点P从O点出发，按以下规律跳动：第1次从O点跳动到OA的中点处，第2次从点跳动到的中点处，第3次从点跳动到的中点处，…，第n次从点跳动到的中点处，按照这样的规律继续跳动到点，，，…，(，n是整数)处，那么点所表示的数为_________．
【答案】
【详解】解：∵A表示的数是，
∴
∵是AO的中点，
∴，
同理，，…，，
∴，
∵在负半轴，
∴点所表示的数是．
故答案是：．
11．已知关于x的方程的解为正整数，则整数k的值为_________．
【答案】3或7．
【详解】解：，
解得，，
∵k为整数，关于x的方程的解为正整数，
∴k-2=1或k-2=5，
解得，k=3或k=7，
故答案为：3或7．
12．如图一，已知数轴上，点表示的数为，点表示的数为，动点从出发，以个单位每秒的速度沿射线的方向向右运动，运动时间为秒
(1)线段__________．
(2)当点运动到的延长线时_________．(用含的代数式表示)
(3)如图二，当秒时，点是的中点，点是的中点，求此时的长度．
(4)当点从出发时，另一个动点同时从点出发，以个单位每秒的速度沿射线向右运动，
①点表示的数为：_________(用含的代数式表示)，
点表示的数为：__________(用含的代数式表示)．
②存在这样的值，使、、三点有一点恰好是以另外两点为端点的线段的中点，请直接写出值．______________．
【答案】(1)；(2)；(3)；(4)①； ②秒或秒或秒
【解析】(1)
解：∵在数轴上，点A表示的数为－6，点B表示的数为8，
∴．
故答案为：14
(2)
∵在数轴上，点表示的数为，点表示的数为，动点从点出发时，以个单位每秒的速度沿射线的方向向右运动，运动时间为秒，
∴，
∴．
故答案为：
(3)
∵点表示的数为，点表示的数为，动点从点出发时，以个单位每秒的速度沿射线的方向向右运动，
当秒时，，
∴，
又∵点是的中点，点是的中点，
∴，，
∴．
∴此时的长度为．
(4)
①设运动时间为，当点从点出发时，以个单位每秒的速度沿射线的方向向右运动，另一个动点同时从点出发，以个单位每秒的速度沿射线向右运动，
∴，，
∴点所表示的数为：，点所表示的数为：，
故答案为：；
②结合①的结论和点所表示的数，可知：
点表示的数为，点所表示的数为：，点所表示的数为：，
分以下三种情况：
若点为中点，则，
∴，
解得：；
若点为中点，则，
∴，
解得：；
若点为中点，则，
∴，
解得：．
综上所述，当为秒或秒或秒时，、、三点中有一点恰好是以另外两点为端点的线段的中点．
13．数学课上李老师说：咱们一起来玩儿一个找原点的游戏吧！
(1)如图1，在数轴上标有A，B两点，已知A，B两点所表示的数互为相反数．
①如果点A所表示的数是，那么点B所表示的数是_______；
②在图1中标出原点O的位置；
(2)图2是小敏所画的数轴，数轴上标出的点中任意相邻两点间的距离都相等．
根据小敏提供的信息，标出隐藏的原点O的位置，并写出此时点C所表示的数是____________；
(3)如图3，数轴上标出若干个点，其中点A，B，C所表示的数分别为a，b，c．若数轴上标出的若干个点中每相邻两点相距1个单位(如AB=1)，且．
①试求a的值；
②若点D也在这条数轴上，且CD=2，求出点D所表示的数．
【答案】(1)①5；②数轴见解析
(2)数轴见解析，点C表示的数是3
(3)①-2；②d=2或d=6
【详解】(1)解：①点A所表示的数是-5，点A、点B所表示的数互为相反数，所以点B所表示的数是5，故答案为：5；②在图1中表示原点O的位置如图所示：
(2)原点O的位置如图所示，点C所表示的数是3．故答案为：3；
(3)解：①由题意得：AC=6，所以c-a=6，又因为c-2a=8，所以a=-2；②设D表示的数为d，因为c-a=6，a=-2，所以c=4，因为CD=2，所以c-d=2或d-c=2，所以d=2或d=6．
14．已知∠AOB=120°，∠COD=60°．
(1)如图1，当∠COD在∠AOB的内部时，若∠AOD=95°，求∠BOC的度数；
(2)如图2，当射线OC在∠AOB的内部，OD在∠AOB的外部时，试探索∠AOD与∠BOC的数量关系，并说明理由；
(3)如图3，当∠COD在∠AOB的外部时，分别在∠AOC内部和∠BOD内部画射线OE，OF，使∠AOE =∠AOC，∠DOF=∠BOD，求∠EOF的度数．
【答案】(1)85°
(2)与互补，理由见解析
(3)当或时，；当时，；当或时，或
【解析】(1)解：∵，，∴，
∵，∴；
(2)与互补；理由如下：
∵，，
∴，∴与互补．
(3)解：设，①当时，如图3，
，，
∵，∴，
∵，∴，
∴， ∴；
②当时，如图，点在的延长线上，
则，，，
∴，，
此时与或重合，
当与重合时，，
当与重合时，，
③当时，如图，
，，
∵，，
，∴；
④当时，如图，点在的延长线上，
则，，∴，此时与或重合，
当与重合时，，当与重合时，；
⑤当时，如图，，，
∵，，，
∴，
综上：当或时，；
当时，；
当或时，或．
15．如图所示，已知直角三角板和直角三角板，，．将两块三角板摆放在一起，且点重合．过点作射线、，且，．
(1)按图1所示位置摆放，则______；
(2)按图2所示位置摆放，求的值；
(3)按图3所示位置摆放，且，求的值．
【答案】(1)40°；(2)40°；(3)．
【详解】解：(1)∵，
∴，
∴，
∵，
∴，
∴，
∴，
故答案是：40°；
(2)∵，，，
∴，
∵，，，
∴，
∴；
(3)设，则，
，
∵，
∴，
∴，即，
∴，解得，
∴，，
∴．