初中数学人教版七年级上册第一章 有理数1.2 有理数1.2.4 绝对值优秀ppt课件

这是一份初中数学人教版七年级上册第一章 有理数1.2 有理数1.2.4 绝对值优秀ppt课件，共30页。PPT课件主要包含了24绝对值，第一章有理数，第1课时绝对值，2有理数，新课导入，讲授新课，a≥0，当堂练习，课堂小结等内容，欢迎下载使用。
1.理解绝对值的概念及性质.（难点、重点）2.会求一个有理数的绝对值.
数轴是规定了原点、正方向、单位长度的直线
只有符号不同的两个数叫做互为相反数.规定：0的相反数是0.
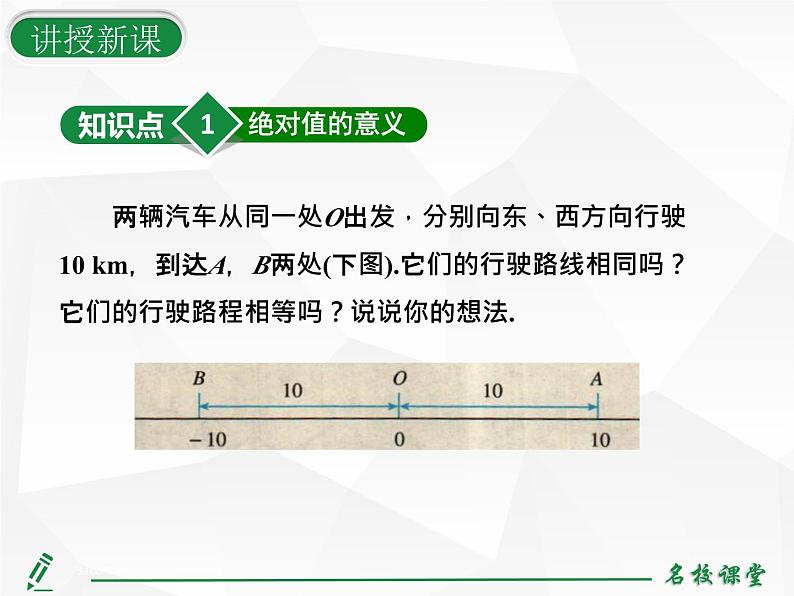
两辆汽车从同一处O出发，分别向东、西方向行驶10 km，到达A，B两处(下图).它们的行驶路线相同吗？它们的行驶路程相等吗？说说你的想法.
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值，用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
1.几何定义：一般地，数轴上表示数a的点与原点的距 离叫做数a的绝对值，记作2.代数定义：一个正数的绝对值是它本身；一个负数 的绝对值是它的相反数；0的绝对值是0；任意一个 数的绝对值为唯一非负数． 用式子表示为：
例1 写出下列各数的绝对值： ，0， ， ，－4.5，－5.
　　求一个数的绝对值的方法：去掉绝对值符号时，必须按照“先判后去”的原则，先判断这个数是正数、0或负数，再根据绝对值的意义去掉绝对值符号，总之要确保其结果为非负数且只有一个．
例2 已知一个数的绝对值是4，则这个数________．
所以绝对值等于4的数有
　 直接求一个数的绝对值是一个解；若已知一个数的 绝对值，反过来求这个数，则有两个解．即如果|x|＝a (a>0)，则x＝±a.
1　－5的绝对值是(　　) A．－5 B．－ C. D．5
2　 的相反数是(　　) A. B．－ C．3 D．－3
|5|=5 |-10|=10|3.5|= 3.5 |100|=100|-3|=3 |50|=50|-4.5|=4.5 |-5000|=5000|0|=0 …..
思考： 一个正数的绝对值是什么？ 一个负数的绝对值是什么？ 0的绝对值是什么？
问题：观察这些表示绝对值的数，它们有什么共同点？
结论1：一个正数的绝对值是正数. 一个负数的绝对值是正数. 0的绝对值是0.
结论2：一个正数的绝对值是它本身. 一个负数的绝对值是它的相反数.
任何一个有理数的绝对值都是非负数!
(1)当a是正数时，｜a｜＝____； (2)当a是负数时，｜a｜＝＿＿； (3)当a=0时，｜a｜＝＿＿＿.
负数的绝对值是它的相反数
相反数、绝对值的联系是什么？
互为相反数的两个数的绝对值相等.
绝对值相等，符号相反的两个数互为相反数.
（1）一个数的绝对值是4 ，则这数是－4. 　　　　　　　 　　　　　　　　　 （2）|3|＞0.　　　　　　 （3）|－1.3|＞0.（4）有理数的绝对值一定是正数.　（5）若a＝－b，则|a|＝|b|.　　　　　　　　（6）若|a|＝|b|，则a＝b.（7）若|a|＝－a，则a必为负数.　　　　 　（8）互为相反数的两个数的绝对值相等.
判断下列说法是否正确.
解：根据题意可知x－4＝0，y－3＝0，所以x＝4，y＝3，故x＋y＝7.
归纳总结： 几个非负数的和为0，则这几个数都为0.
1.判断并改错：（1）一个数的绝对值等于本身,则这个数一定是正数 ( )（2）一个数的绝对值等于它的相反数,这个数一定是 负数； ( )（3）如果两个数的绝对值相等,那么这两个数一定 相等； ( )（4）如果两个数不相等,那么这两个数的绝对值 一定不等； ( )（5）有理数的绝对值一定是非负数. ( )
|3|=3；|3.14|=3.14； |-2.8|=2.8.
| b |= (b＜0)
| a – b | = （a＞b）
6.正式排球比赛对所用的排球重量是有严格规定的，现检查5个排球的重量，超过规定重量的克数记作正数，不足规定重量的克数记作负数，检查结果如下：问题：指出哪个排球的质量好一些，并用绝对值的知识加以说明.
答：第五个排球的质量好一些，因为它的绝对值最小，也就是离标准质量的克数最近.
1．数轴上表示数a的点与原点的距离叫做数a的绝对值.2．绝对值的性质 (1)|a|≥0； (2)