+湖北省武汉市部分学校2023-2024学年九年级下学期开学数学试卷+

这是一份+湖北省武汉市部分学校2023-2024学年九年级下学期开学数学试卷+，共24页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.下列标志图中，既是轴对称图形，又是中心对称图形的是( )
A. B. C. D.
2.从左面观察如图所示的几何体，看到的平面图形是( )
A.
B.
C.
D.
3.一元二次方程3x2+4x−1=0的根的情况为( )
A. 有两个相等的实数根B. 有两个不相等的实数根
C. 没有实数根D. 无法确定
4.下列图形中，一定相似的是( )
A. 一条直线截三角形两边所得的三角形与原三角形
B. 有一个内角为80°的两个等腰三角形
C. 两个长方形
D. 有一个内角为80°的两个菱形
5.下列四个命题中不正确的是( )
A. 直径是弦
B. 三角形的外心到三角形三个顶点的距离都相等
C. 顶点在圆周上的角是圆周角
D. 半径相等的两个半圆是等弧
6.下表中所列的x，y的6对值是二次函数y=ax2+bx+c的图象上的点所对应的坐标：
若(x1,y1)，(x2,y2)是该函数图象上的两点，根据表中信息，以下论断正确的是( )
A. 当x1B. 当y1>y2时，x1C. 该函数的最小值为3
D. 当x1=1+n，x2=1−n时(n为常数)，y1=y2
7.如图所示，某幼儿园有一道长为16米的墙，计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.则该矩形草坪BC边的长是( )
A. 12
B. 18
C. 20
D. 12或20
8.如图，滑雪场有一坡角为20°的滑雪道，滑雪道的长AC为100米，则滑雪道的坡顶到坡底的竖直高度AB的长为( )
A. 100cs20∘B. 100sin20∘C. 100cs20°D. 100sin20°
9.如图，弧长为半圆的弓形在坐标系中，圆心在(0,2).将弓形沿x轴正方向无滑动滚动，当圆心经过的路径长为2021π时，圆心的横坐标是( )
A. 2020πB. 1010π+2020C. 2021πD. 1011π+2020
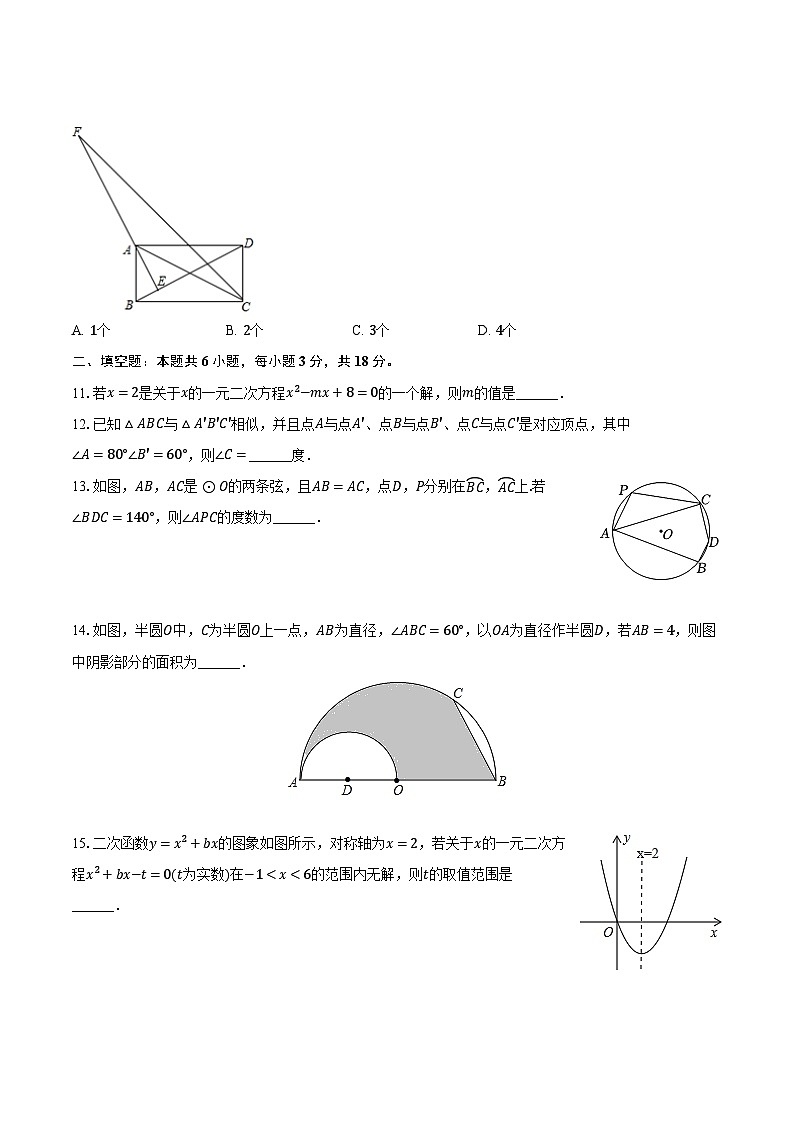
10.如图，矩形ABCD中，AE⊥BD于点E，CF平分∠BCD，交EA的延长线于点F，且BC=4，CD=2，给出下列结论：①∠BAE=∠CAD；②∠DBC=30°；③AE=45 5；④AF=2 5，其中正确结论的个数有( )
A. 1个B. 2个C. 3个D. 4个
二、填空题：本题共6小题，每小题3分，共18分。
11.若x=2是关于x的一元二次方程x2−mx+8=0的一个解，则m的值是______．
12.已知△ABC与△A′B′C′相似，并且点A与点A′、点B与点B′、点C与点C′是对应顶点，其中∠A=80°∠B′=60°，则∠C=______度．
13.如图，AB，AC是⊙O的两条弦，且AB=AC，点D，P分别在BC，AC上.若∠BDC=140°，则∠APC的度数为______．
14.如图，半圆O中，C为半圆O上一点，AB为直径，∠ABC=60°，以OA为直径作半圆D，若AB=4，则图中阴影部分的面积为______．
15.二次函数y=x2+bx的图象如图所示，对称轴为x=2，若关于x的一元二次方程x2+bx−t=0(t为实数)在−116.在平行四边形ABCD的边AB和AD上分别取点E和F，使AE=13AB，AF=14AD，连接EF交对角线AC于G，则AGAC的值是______．
三、计算题：本大题共1小题，共8分。
17.为弘扬中华传统文化，黔南州近期举办了中小学生“国学经典大赛”.比赛项目为：A.唐诗；B.宋词；C.论语；D.三字经．比赛形式分“单人组”和“双人组”．
(1)小丽参加“单人组”，她从中随机抽取一个比赛项目，恰好抽中“三字经”的概率是多少？
(2)小红和小明组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次，则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少？请用画树状图或列表的方法进行说明．
四、解答题：本题共7小题，共64分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题8分)
(1)计算：(1− 3)0+|− 2|−(−1)2015+(14)−1
(2)解方程：(x+4)2=5(x+4)
19.(本小题8分)
如图，AB为⊙O的直径，弦CD⊥AB于点P，CD=4 3，AP：PB=3：1．
(1)求⊙O的半径；
(2)求图中阴影部分的面积．
20.(本小题8分)
如图，已知直线l：y=x+4与反比例函数y=kx(x<0)的图象交于点A(−1,n)，直线l′经过点A，且与l关于直线x=−1对称．
(1)求反比例函数的解析式；
(2)求图中阴影部分的面积；
(3)已知直线l：y=x+4与反比例函数y=kx(x<0)的图象交于点另一点B，P在平面内，若以点A，B，P，O为顶点的四边形是平行四边形，请直接写出所有符合条件点P的坐标．
21.(本小题8分)
如图，是由边长为1的小正方形构成的6×6网格，每个小正方形的顶点叫做格点，⊙O经过A、B、C、D四个格点，仅用无刻度的直尺在给定的网格中按要求画图(画图过程中起辅助作用的用虚线表示，画图结果用实线表示，并用黑色水笔描黑)
(1)如图1，判断圆心O ______(填“是”或“不是”)在格点上，并在图1中标出格点O；
(2)在图1中画出⊙O的切线CG(G为格点)；
(3)在图2中画出BC的中点E；
22.(本小题10分)
如图，在△ABC中，D，E分别是AB，AC上的点，∠AED=∠ABC，∠BAC的平分线AF交DE于点G，交BC于点F．
(1)求证：△AGE∽△AFB．
(2)若AGGF=32，GE=2，求BF的长．
23.(本小题10分)
用一条直线截三角形的两边，若所截得的四边形对角互补，则称该直线为三角形第三条边上的逆平行线．如图1，DE为△ABC的截线，截得四边形BCED，若∠BDE+∠C=180°，则称DE为△ABC边BC的逆平行线．
如图2，已知△ABC中，AB=AC，过边AB上的点D作DE/​/BC交AC于点E，过点E作边AB的逆平行线EF，交边BC于点F．
(1)求证：DE是边BC的逆平行线．
(2)点O是△ABC的外心，连接CO.求证：CO⊥FE．
(3)已知AB=5，BC=6，过点F作边AC的逆平行线FG，交边AB于点G．
①试探索AD为何值时，四边形AGFE的面积最大，并求出最大值；
②在①的条件下，比较AD+BG______AB大小关系．(“<、>或=”)
24.(本小题12分)
如图1，抛物线y=−x2+bx+c过点A(−1,0)，点B(3,0)，与y轴交于点C.在x轴上有一动点E(m,0)(0
(1)求抛物线的解析式；
(2)当m=1时，点D是直线ME上的点且在第一象限内，若△ACD是以CA为斜边的直角三角形，求点D的坐标；
(3)如图2，连接BC，BC与ME交于点F，连接AF，△ACF和△BFM的面积分别为S1和S2，当S1=4S2时，求点E坐标．
答案和解析
1.【答案】B
【解析】解：A、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，故A选项错误；
B、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故B选项正确；
C、此图形旋转180°后不能与原图形重合，此图形不是中心对称图形，是轴对称图形，故C选项错误；
D、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，也不是轴对称图形，故D选项错误．
故选：B．
根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．
此题主要考查了中心对称图形与轴对称的定义，根据定义得出图形形状是解决问题的关键．
2.【答案】B
【解析】解：从左边看，底层是两个小正方形，上层左边一个小正方形，
故选：B．
根据从左边看得到的图形是左视图，可得答案．
本题考查了简单组合体的三视图，熟知从左边看得到的图形是左视图是解答本题的关键．
3.【答案】B
【解析】解：∵a=3，b=4，c=−1，
∴Δ=b2−4ac=42−4×3×(−1)=16+12=38>0，
∴一元二次方程3x2+4x−1=0有两个不相等的实数根．
故选：B．
根据一元二次方程根的判别式，即可得出Δ=38>0，进而可得出该方程有两个不相等的实数根．
本题考查了一元二次方程根的判别式，牢记“当Δ>0时，方程有两个不相等的实数根”是解题的关键．
4.【答案】D
【解析】解：A、一条直线截三角形两边所得的三角形与原三角形不一定相似，故A选项不符合题意；
B、有一个内角为80°的两个等腰三角形不一定相似，故B选项不符合题意；
C、两个长方形不一定相似，故C选项不符合题意；
D、有一个内角为80°的两个菱形一定相似，故D选项符合题意．
故选：D．
由相似三角形的判定方法依次判断可求解．
本题考查了相似三角形的判定，熟练运用相似三角形的判定是本题的关键．
5.【答案】C
【解析】解：A.直径是弦，直径是圆中最长的弦，因此选项A不符合题意；
B.三角形的外心是三角形三条边中垂线的交点，因此三角形的外心到三角形三个顶点的距离都相等，因此选项B不符合题意；
C.顶点在圆上，两边与圆还有另一个交点的角是圆周角，因此选项C符合题意；
D.半径相等的两个半圆，放在一起能完全重合，因此是等弧，所以选项D不符合题意．
故选：C．
根据直径、弦的定义，三角形的外心，圆周角以及等弧的定义逐项进行判断即可．
本题考查圆的认识，圆周角，三角形的外心，理解直径与弦的关系，圆周角的定义，三角形外心的性质是正确判断的关键．
6.【答案】D
【解析】解：根据表格中的数据可得：抛物线开口向上，在对称轴左边，y随x的增大而减小，在对称轴的右边，y随x的增大而增大，故A，B选项错误，不符合题意；
根据表格可知，抛物线的对称轴为直线x=1，顶点坐标的纵坐标的值为最小值，最小值不是3，故C选项错误，不合题意；
∵x1+x22=1，
∴y1=y2，故D选项正确，符合题意；
故选：D．
观察表格中的数据11，6，3，6，11可知抛物线开口向上，在对称轴左边，y随x的增大而减小，在对称轴的右边，y随x的增大而增大；当x=−1和3时，y的值都是6，所以对称轴为直线x=1，顶点坐标的纵坐标的值为最小值；根据x1+x22=1可知这两个点关于对称轴x=1对称，所以y1=y2．
本题考查了二次函数的图象与性质，根据表格判断出抛物线的开口方向，对称轴，最值是解题的关键．
7.【答案】A
【解析】解：设草坪BC的长为x米，则宽为32−x2，
由题意得，x⋅32−x2=120，
解得：x1=12，x2=20，
∵墙为16米，
∴x=20不合题意．
故x=12．
故选：A．
设草坪BC的长为x米，则宽为32−x2，根据面积为120平方米，列方程求解．
本题考查了一元二次方程的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程求解．
8.【答案】D
【解析】【试题解析】
【分析】
本题考查的是解直角三角形的应用−坡度坡角问题，掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键．根据正弦的定义进行解答即可．
【解答】
解：∵sin∠C=ABAC，
∴AB=AC⋅sin∠C=100sin20°，
故选D．
9.【答案】D
【解析】解：由题知，图形每旋转一周，圆心的路径循环一次，且路径长度刚好为以2为半径的圆的周长，
即4π，
2021π÷4π=50514(圈)，
即当圆心经过的路径长为2021π时，图形旋转了50514圈，
∵图形每旋转一圈横坐标增加2π+4，
∴当图形旋转505圈时的横坐标为(2π+4)×505=1010π+2020，
再转14圈横坐标增加14×4π=π，
∴当圆心经过的路径长为2021π时，圆心的横坐标是1010π+2020+π=1011π+2020，
故选：D．
由题知，圆心的运动轨迹是一段线段和四分之一圆弧循环出现组成的图形，根据循环规律计算出横坐标即可．
本题主要考查图形的变化规律，掌握圆心运动路径的变化规律是解题的关键．
10.【答案】C
【解析】【分析】
本题考查了矩形的性质，相似三角形的判定和性质，三角形的外角的性质，角平分线的定义，熟练掌握相似三角形的判定和性质是解题的关键，根据余角的性质得到∠BAE=∠ADB，等量代换得到∠BAE=∠CAD，故①正确；根据锐角三角函数的定义得到tan∠DBC=CDBC=12，于是得到∠DBC≠30°，故②错误；由勾股定理得到BD= BC2+CD2=2 5，根据相似三角形的判定与性质得到AE=45 5，故③正确；根据角平分线的定义得到∠BCF=45°，求得∠ACF=45°−∠ACB，推出∠EAC=2∠ACF，根据三角形外角的性质得到∠EAC=∠ACF+∠F，得到∠ACF=∠F，根据等腰三角形的判定得到AF=AC，于是得到AF=2 5，故④正确．
【解答】
解：在矩形ABCD中，∠BAD=90°，∵AE⊥BD，
∴∠AED=90°，
∴∠ADE+∠DAE=∠DAE+∠BAE=90°，
∴∠BAE=∠ADB，
由矩形的性质易得∠CAD=∠ADB，
∴∠BAE=∠CAD，故①正确；
∵BC=4，CD=2，
∴tan∠DBC=CDBC=12，
∴∠DBC≠30°，故②错误；
∵BD= BC2+CD2=2 5，
又∵AB=CD=2，AD=BC=4，
由①易证△ABE∽△DBA，
∴AEAD=ABBD，
即AE4=22 5，
∴AE=45 5；故③正确；
∵CF平分∠BCD，
∴∠BCF=45°，
∴∠ACF=45°−∠ACB，
∵AD/​/BC，
∴∠DAC=∠BAE=∠ACB，
∴∠EAC=90°−2∠ACB，
∴∠EAC=2∠ACF，
∵∠EAC=∠ACF+∠F，
∴∠ACF=∠F，
∴AF=AC，
∵AC=BD=2 5，
∴AF=2 5，故④正确；
故选C．
11.【答案】6
【解析】解：把x=2代入方程，得
4−2m+8=0，
解得m=6．
故答案为：6．
先把x=2代入方程，可得关于m的一元一次方程，解即可．
本题考查了一元二次方程的解，解题的关键是代入．
12.【答案】40
【解析】解：∵△ABC∽△A′B′C′，∠B′=60°，
∴∠B=∠B′=60°，
∴∠C=180°−∠A−∠B=180°−80°−60°=40°．
故答案为：40．
根据相似三角形对应角相等求出∠B=∠B′，再利用三角形内角和等于180°列式进行计算即可得解．
本题考查了相似三角形对应角相等，三角形内角和定理，熟记性质并准确找出对应角是解题的关键．
13.【答案】110°
【解析】解：在圆内接四边形ABCD中，∠BDC=140°，
∴∠BAC=180°−∠BDC=180°−140°=40°，
∵AB=AC，
∴∠ABC=12(180°−40°)=70°，
∴∠APC=180°−70°=110°，
故答案为：110°．
根据圆内接四边形对角互补求得∠BAC的度数，根据等腰三角形的性质可求得∠ABC的度数，进而根据圆内接四边形对角互补即可求得∠APC的度数．
此题主要考查了圆的内接四边形的性质，圆周角定理，在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角或弧的度数的一半．
14.【答案】56π+ 3
【解析】解：如图，连接OC．
∵AB=4，
∴OA=OB=2，OD=AD=1，
∵∠ABC=60°，OB=OC，
∴∠BOC=60°，
∴S弓形BC=S扇形OBC−S△OBC=60π×22360−12×2× 3=2π3− 3，
∵S半圆AOD=12×π×12=12π，
S半圆ABO=12π×22=2π
∴S阴影=S半圆ABO−S半圆AOD−S弓形BC
=2π−12π−(2π3− 3)
=5π6+ 3，
故答案为5π6+ 3．
求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积．求阴影面积常用的方法：①直接用公式法；②和差法；③割补法．
本题考查了扇形的面积的相关计算，熟练运用割补法和扇形面积计算公式是解题的关键．
15.【答案】t<−4或t≥12
【解析】解：∵抛物线y=x2+bx的对称轴为x=2，
∴x=−b2=2，
∴b=−4，
∴抛物线的解析式为y=x2−4x．
当x=−1时，y=5；
当x=2时y=−4；
当x=6时y=12．
结合图象可得：
当t<−4或t≥12时，直线y=t与抛物线y=x2−4x在−1即关于x的一元二次方程x2−4x−t=0(t为实数)在−1故答案为t<−4或t≥12．
根据抛物线的对称轴方程可求出抛物线的解析式，要使关于x的一元二次方程x2+bx−t=0(t为实数)在−1本题主要考查了抛物线的性质、抛物线上点的坐标特征等知识，运用数形结合的思想是解决本题的关键．
16.【答案】17
【解析】解：如图，在AD上取点H，使AH=34AD，连接BH交AC于O，
则AGAO=13，即AG=13AO，
又∵AD/​/BC，
∴△AOH∽△COB，
∴AOCO=AHCB=34，CO=43AO，
∴AGAC=AGAO+CO=13AOAO+43AO=17．
故答案为17．
根据题意在AD上截取AH=34AD，得到AG与AO的关系，然后由相似三角形得到OC与AO的关系，代入AGAC求出比值．
本题考查相似三角形的判定与性质，以及平行四边形的性质．
17.【答案】解：(1)她从中随机抽取一个比赛项目，恰好抽中“三字经”的概率是14；
(2)画树状图为：
共有12种等可能的结果数，其中恰好小红抽中“唐诗”且小明抽中“宋词”的结果数为1，
所以恰好小红抽中“唐诗”且小明抽中“宋词”的概率是112．
【解析】(1)直接利用概率公式求解；
(2)先画树状图展示所有12种等可能的结果数，再找出恰好小红抽中“唐诗”且小明抽中“宋词”的结果数，然后根据概率公式求解．
本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．
18.【答案】解：(1)原式=1+ 2+1+4= 2+6；
(2)方程移项得：(x+4)2−5(x+4)=0，
分解因式得：(x+4)(x+4−5)=0，
解得：x1=−4，x2=1．
【解析】(1)原式第一项利用零指数幂法则计算，第二项利用绝对值的代数意义化简，第三项利用乘方的意义计算，最后一项利用负整数指数幂法则计算即可得到结果；
(2)方程移项后，利用因式分解法求出解即可．
此题考查了实数的运算，以及解一元二次方程−因式分解法，熟练掌握运算法则是解本题的关键．
19.【答案】解：(1)连接OC，OD，
设AP=3x，PB=x，则AB=4x，OC=2x，OP=x，
∵CD⊥AB，
∴CP=DP=2 3，
∴x2+(2 3)2=(2x)2，
解得：x=2或x=−2(舍去)，
∴OC=4，
∴⊙O的半径为4；
(2)∵OP=2，OC=4，
∴在Rt△OCP中，∠OCP=30°，∠COP=60°，
∴∠COD=120°，
∵S阴影=S扇形OCD−S△OCD
=120°⋅π⋅42360∘−12×4 3×2
=163π−4 3，
∴阴影部分的面积为：16π3−4 3．
【解析】(1)连接OC，OD，利用垂径定理得CP=2 3，AP=3x，PB=x，则AB=4x，OC=2x，OP=x，利用勾股定理可得结果；
(2)根据OP=2，OC=4，利用直角三角形的性质易得∠COD=120°，利用扇形和三角形的面积公式，求得阴影部分面积．
本题主要考查了垂径定理，勾股定理，直角三角形的性质和扇形面积公式，作出适当的辅助线，数形结合是解答此题的关键．
20.【答案】解：(1)直线l：y=x+4与反比例函数y=kx(x<0)的图象交于点A(−1,n)，
把A(−1,n)代入l：y=x+4，得：n=−1+4=3，
∴A(−1,3)，
将A(−1,3)代入反比例函数y=kx(x<0)，得：3=k−1，
∴k=−3，
∴反比例函数的解析式为y=−3x(x<0)；
(2)根据直线l：y=x+4，可得直线l与x轴的交点为(−4,0)，
∵直线l′经过点A，且与l关于直线x=−1对称，
∴直线l′与x轴的交点为(2,0)，
设直线l′：y=k2x+b，
将A(−1,3)，(2,0)代入解析式得：
3=−k2+b0=2k2+b，
解得k2=−1b=2，
∴直线l′：y=−x+2，
∴直线l′与y轴的交点坐标为(0,2)，
结合图形阴影部分面积=直线l、直线l′与x轴围成的三角形面积−直线l′与x轴、y轴围成的三角形面积，
∴S阴影=[2−(−4)]×32−2×22=9−2=7；
(3)∵直线l：y=x+4与反比例函数y=−3x(x<0)的图象交于点另一点B，联立得：
y=x+4y=−3x，
解得：x1=−1y1=3或x2=−3y2=1，
∴B(−3,1)，
∴四边形ABOP是平行四边形，则如图所示，

当AB为平行四边形一边时，
则OP/​/AB，
∴OP的直线表达式为y=x，
∵A(−1,3)、B(−3,1)，O(0,0)，
∴①当平行四边形为ABP1O时，
P1点的横坐标为0−[−1−(−3)]=−2，
P1点的纵坐标为0−(3−1)=−2，
∴P1点的坐标为(−2,−2)，
②当平行四边形为ABOP2时，
P2点的横坐标为0+[−1−(−3)]=2，
P2点的纵坐标为0+(3−1)=2，
∴P2点的坐标为(2,2)，
③当AB为平行四边形的对角线时，
平行四边形AP3BO时，
P3点的横坐标为−3−[0−(−1)]=−4，
P3点的纵坐标为1−(0−3)=4，
∴P3点的坐标为(−4,4)．
【解析】(1)根据A(−1,n)，l：y=x+4，算出点A坐标，再将点A坐标代入反比例函数，即可解答．
(2)根据题意求出直线l′的解析式，结合图形阴影部分面积=直线l、直线l′与x轴围成的三角形面积−直线l′与x轴、y轴围成的三角形面积，算出直线l、直线l′与坐标轴的交点坐标即可解答．
(3)根据直线l和反比例函数的解析式，可以得到B点坐标，通过ABO三点，根据平行四边形的性质，得到对应的P点坐标．
本题考查了反比例函数与一次函数结合的综合题，涉及到用待定系数法求反比例函数以及一次函数，平行四边形的性质，熟知该性质是解题的关键．
21.【答案】是
【解析】解：(1)如图：
圆心O在弦AB，CD的垂直平分线上，由图可知，O在格点上，
故答案为：是；
(2)如图：
CG即为所求；
(3)如图：
由方格的特征，取BC的中点K，连接并延长OK交⊙O于E，
点E即为所求．
(1)画出弦AB，CD的垂直平分线可得答案；
(2)连接OC，取格点G，使CG⊥OC即可；
(3)由方格的特征，取BC的中点K，连接并延长OK交⊙O于E，即得BC的中点．
本题考查作图−应用与设计作图，涉及垂径定理，全等三角形等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
22.【答案】证明：(1)∵AF平分∠BAC，
∴∠EAG=∠BAF，
∵∠AED=∠ABC，
∴△AEG∽△ABF；
(2)解：∵AGGF=32，
∴AGAF=35，
∵△AEG∽△ABF，
∴AGAF=GEBF，
而GE=2，
∴BF=103．
【解析】(1)根据两组对应角相等可证明三角形相似；
(2)根据相似三角形的对应边成比例可以进行计算．
本题考查相似三角形的判定和性质，解题的关键是熟练掌握相似三角形的判定方法，属于中考常考题型．
23.【答案】=
【解析】(1)证明：
∵AB=AC，
∴∠B=∠ACB
∵DE/​/BC，
∴∠BDE+∠B=180°.∠BDE+∠ACB=180°．
∴DE是边BC的逆平行线．
(2)证明：如图，连接AO，
∵EF是边BA的逆平行线，
∴∠AEF+∠B=180°，
∵∠AEF+∠FEC=180°，
∴∠FEC=∠B，
∵点O是△ABC的外心，
∴OA=OC，OA平分∠BAC，
∴∠OAC=∠OCA，∠BAO=∠OAC，
∵∠BAO+∠B=90°，
∴∠FEC+∠ACB=90°，
∴CO⊥FE，
(3)解：①设FC=x，BF=6−x，S四边形AGFE=y，
∵∠FEC=∠B，∠FCE=∠ACB，
∴△FEC∽△ABC．
∴(FCAB)2=S△EFCS△BAC，
∴S△EFC=1225x2，
同理可得S△BFG=1225(6−x)2
∴y=S△ABC−S△EFC−S△BFG=12−2425[x2+(6−x)2]=−2425(x−3)2+8425，
∴当 x=3 时，有 AD=75，此时 y 有最大值，最大值为8425．
②在①的条件下CF=BF=3，如图，连接DF，
∵BF=CF，∠B=∠C，BD=CE，
∴△BDF≌△CEF(SAS)，
∴∠BDF=∠CEF，∠BFD=∠EFC，
∴∠BFE=∠DFC，∠AEF=∠ADF．
∵∠AEF+∠B=180°，∠A+∠BFE=180°，
∴∠C+∠ADF=180°，∠A+∠DFC=180°．
∴FD为边AC的逆平行线，
由题意可知D与G点重合，
∴AD+BG=AB，
故答案为：=．
(1)由条件可证得∠B=∠ACB，则∠BDE+∠B=180°.∠BDE+∠ACB=180°，结论得证；
(2)连接AO，证得∠FEC=∠B，由OA=OC可得∠OAC=∠OCA，∠BAO=∠OAC，证出∠FEC+∠ACB=90°，即CO⊥FE，
(3)①设FC=x，则BF=6−x，证△FEC∽△ABC，可得S△EFC=1225x2，同理可得S△BFG=1225(6−x)2，四边形AGFE的面积可表示为S△ABC−S△EFC−S△BFG，利用二次函数的性质可求出最大值；
②由①知点F为BC的中点，连接DF，根据EF为AB边的逆平行线，可证得DF为AC边的逆平行线，则G点与D点重合，则AD+BG=AB．
本题是新定义结合圆的综合题，综合考查了等腰三角形的性质、相似三角形的判定与性质、外心的定义、二次函数的性质等知识，关键是读懂定义并根据图形的性质解答．
24.【答案】解：(1)∵抛物线y=−x2+bx+c过点A(−1,0)，点B(3,0)，
∴−1−b+c=0−9+3b+c=0，
解：b=2c=3，
∴该抛物线的解析式为y=−x2+2x+3；
(2)令x=0，得y=3，
∴C(0,3)，
当m=1时，设D(1,y)，
∵△ACD是以CA为斜边的直角三角形，
∴AD2+CD2=AC2，
∴22+y2+12+(3−y)2=12+32，
解得：y1=1，y2=2，
∴点D的坐标为(1,1)或(1,2)；
(3)设直线BC的解析式为y=kx+d，则3k+d=0d=3，
解得：k=−1d=3，
∴直线BC的解析式为y=−x+3，
∵E(m,0)，ME⊥x轴，0∴M(m,−m2+2m+3)，F(m,−m+3)，
又A(−1,0)，B(3,0)，C(0,3)，
∴AB=3−(−1)=4，OC=3，EF=−m+3，MF=−m2+2m+3−(−m+3)=−m2+3m，BE=3−m，
∴S1=S△ACF=S△ABC−S△ABF=12AB⋅(OC−EF)=12×4[3−(−m+3)]=2m，
S2=S△BFM=12MF⋅BE=12(−m2+3m)(3−m)，
∵S1=4S2，
∴2m=12(−m2+3m)(3−m)，
化简得：m(m2−6m+8)=0，
∵0∴m2−6m+8=0，
解得：m1=2，m2=4(不符合题意，舍去)，
∴点E的坐标为(2,0)．
【解析】(1)运用待定系数法即可求得抛物线解析式；
(2)当m=1时，设D(1,y)，根据勾股定理建立方程求解即可得出答案；
(3)利用待定系数法可得直线BC的解析式为y=−x+3，由题意得E(m,0)，M(m,−m2+2m+3)，F(m,−m+3)，利用三角形面积公式可得S1=S△ACF=S△ABC−S△ABF=2m，S2=S△BFM=12MF⋅BE=12(−m2+3m)(3−m)，根据S1=4S2，建立方程求解即可得出答案．
本题是二次函数综合题，考查了待定系数法求函数解析式，二次函数的综合应用，直角三角形性质，勾股定理的应用，三角形面积等知识，解题的关键是用含m的代数式表示S1、S2列方程．x
…
−2
−1
0
3
4
…
y
…
11
6
3
6
11
…