高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直图片ppt课件

这是一份高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直图片ppt课件，共50页。PPT课件主要包含了任意一条，l⊥α，预习自测，两条相交直线，a∩b＝P，∠PAO，a∥b，垂线段，答案C等内容，欢迎下载使用。
| 自 学 导 引 |
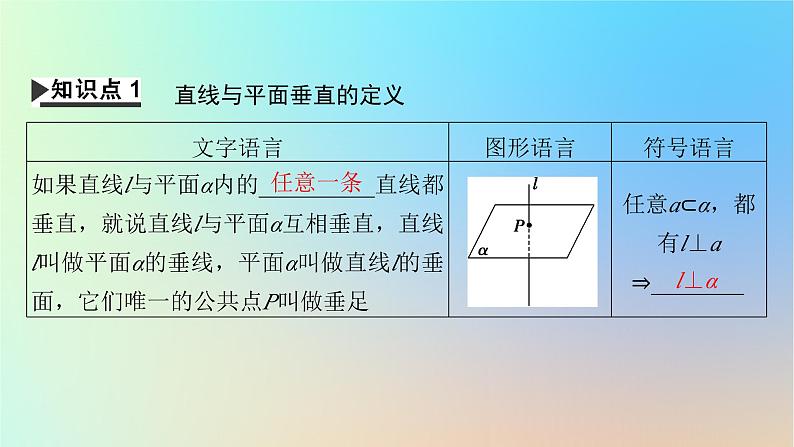
　　　　直线与平面垂直的定义
【预习自测】直线l⊥平面α，直线m⊂α，则l与m不可能(　　)A．平行B．相交C．异面　D．垂直【答案】A【解析】由直线与平面垂直的定义可知，l⊥m，l与m可能相交或异面，但不可能平行．
直线与平面垂直定义中的关键词“任意一条直线”是否可以换成“所有直线”“无数条直线”？【提示】定义中的“任意一条直线”与“所有直线”是等效的，但是不可说成“无数条直线”，因为一条直线与某平面内无数条平行直线垂直，该直线与这个平面不一定垂直．
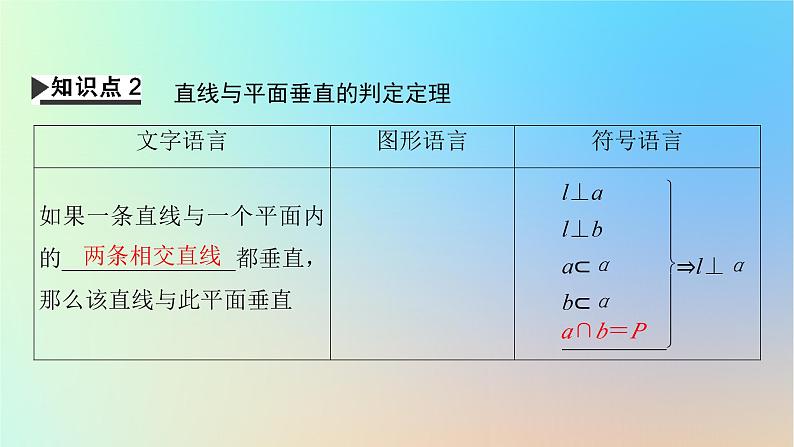
　　　　直线与平面垂直的判定定理
【预习自测】一条直线和三角形的两边同时垂直，则这条直线和三角形的第三边的位置关系是(　　)A．平行　　B．垂直C．相交不垂直　　D．不确定【答案】B【解析】直线和三角形两边垂直，由线面垂直的判定定理知，直线垂直三角形所在平面，则直线垂直于三角形的第三边．
　　　　直线与平面所成的角1．定义(1)一条直线AP与平面α相交，但不垂直，这条直线叫这个平面的斜线，斜线与平面的交点A叫斜足．(2)过斜线上斜足外的一点P向平面α引垂线PO，过垂足O和斜足A的直线OA叫斜线在这个平面上的射影．(3)平面的一条斜线和它在平面上的射影所成的______，叫做这条直线和这个平面所成的角．
2．范围：设直线与平面所成的角为θ，则0°≤θ≤90°．3．画法：如图所示，直线AP与平面α所成的角是__________．
【预习自测】若斜线段AB是它在平面α上的射影长的2倍，则AB与平面α所成角的大小为(　　)A．60°B．45°C．30°D．90°【答案】A
　　　　直线与平面垂直的性质定理
【预习自测】判断下列命题是否正确．(正确的画“√”，错误的画“×”)(1)垂直于同一条直线的两个平面互相平行．(　　)(2)垂直于同一平面的两条直线互相平行．(　　)(3)一条直线在平面内，另一条直线与这个平面垂直，则这两条直线互相垂直．(　　)【答案】(1)√　(2)√　(3)√【解析】由线面垂直的定义和性质可知(1)，(2)，(3)均正确．
　　　　距离1．点到平面的距离：过一点作垂直于已知平面的直线有且只有一条，且该点与垂足间的线段，叫做这个点到该平面的_________，垂线段的长度叫做这个点到该平面的________．2．直线到平面的距离：一条直线与一个平面平行时，这条直线上任意一点到这个平面的距离，叫做这条直线到这个平面的距离．3．两个平行平面间的距离：如果两个平面平行，那么其中一个平面内的任意一点到另一个平面的距离都______，我们把它叫做这两个平行平面间的距离．
| 课 堂 互 动 |
题型1　线面垂直的定义及判定定理的理解　　　　下列说法中正确的个数是(　　)①若直线l与平面α内的两条相交直线都垂直，则l⊥α；②若直线l与平面α内的任意一条直线垂直，则l⊥α；③若直线l不垂直于α，则α内没有与l垂直的直线；④若直线l不垂直于α，则α内也可以有无数条直线与l垂直．A．0　　B．1C．2　　D．3【答案】D
【解析】由直线和平面垂直的判定定理知①正确；由直线与平面垂直的定义知②正确；当l与α不垂直时，l可能与α内的无数条直线垂直，故③错误；④正确．
1．对于线面垂直的定义要注意“直线垂直于平面内的所有直线”说法与“直线垂直于平面内无数条直线”不是一回事，后者说法是不正确的，它可以使直线与平面斜交、平行或直线在平面内．2．判定定理中要注意必须是平面内两相交直线．
1．下列说法中，正确的是(　　)A．若直线l与平面α内无数条直线垂直，则l⊥αB．若直线l垂直于平面α，则l与平面α内的直线可能相交，可能异面，也可能平行C．若a∥b，a⊂α，l⊥α，则l⊥bD．若a⊥b，b⊥α，则a∥α【答案】C
【解析】当l与α内的任何一条直线都垂直时，l⊥α，故A错；当l⊥α时，l与α内的直线相交或异面，但不会平行，故B错；C显然是正确的；而D中，a可能在α内，所以D错误．
题型2　线面垂直判定定理的应用　　　　如图，在△ABC中，∠ABC＝90°，D是AC的中点，S是△ABC所在平面外一点，且SA＝SB＝SC．(1)求证：SD⊥平面ABC；(2)若AB＝BC，求证：BD⊥平面SAC．
证明：(1)如图，∵SA＝SC，D为AC的中点，∴SD⊥AC．连接BD．在Rt△ABC中，有AD＝DC＝DB．∴△SDB≌△SDA(SSS)，∴∠SDB＝∠SDA＝90°，∴SD⊥BD．又∵AC∩BD＝D，∴SD⊥平面ABC．
(2)∵AB＝BC，D是AC的中点，∴BD⊥AC．又由(1)知SD⊥BD，且AC∩SD＝D，∴BD⊥平面SAC．
证明线面垂直的方法(1)线线垂直证明线面垂直：①定义法(不常用，但由线面垂直可得出线线垂直)；②判定定理最常用：着力寻找平面内两条相交直线(有时作辅助线)；结合平面图形的性质(如勾股定理逆定理、等腰三角形底边中线等)及一条直线与平行线中一条垂直也与另一条垂直等结论来论证线线垂直．(2)平行转化法(利用推论)①a∥b，a⊥α⇒b⊥α；②α∥β，a⊥α⇒a⊥β．
∴PC2＋BC2＝PB2，∴△PCB为直角三角形，PC⊥BC．∵PC·BC＝PB·CF，∴PB⊥CF．又∵EF⊥PB，EF∩CF＝F，∴PB⊥平面CEF．
题型3　直线与平面所成的角　　　　如图，在Rt△BMC中，斜边BM＝5，它在平面ABC上的射影AB长为4，∠MBC＝60°，求直线MC与平面ABC所成角的正弦值．解：由题意知A是M在平面ABC上的射影，∴MA⊥平面ABC．∴MC在平面CAB上的射影为AC．∴∠MCA即为直线MC与平面CAB所成的角．
求斜线与平面所成角的步骤(1)作图：作(或找)出斜线在平面内的射影，作射影要过斜线上一点作平面的垂线，再过垂足和斜足作直线，注意斜线上点的选取以及垂足的位置要与问题中已知量有关，才能便于计算．(2)证明：证明某平面角就是斜线与平面所成的角．(3)计算：通常在垂线段、斜线和射影所组成的直角三角形中计算．
3．如图所示，在正方体ABCD－A1B1C1D1中，E是棱DD1的中点．求直线BE与平面ABB1A1所成的角的正弦值．
解：如图，取AA1的中点M，连接EM，BM．因为E是DD1的中点，四边形ADD1A1为正方形，所以EM∥AD．又因为在正方体ABCD－A1B1C1D1中，AD⊥平面ABB1A1，所以EM⊥平面ABB1A1．
从而BM为直线BE在平面ABB1A1上的射影，∠EBM即为直线BE与平面ABB1A1所成的角．
题型4　线面垂直性质定理的应用　　　　如图，在四棱锥P－ABCD中，底面ABCD是矩形，AB⊥平面PAD，AD＝AP，E是PD的中点，M，N分别在AB，PC上，且MN⊥AB，MN⊥PC．求证：AE∥MN．
证明：因为AB⊥平面PAD，AE⊂平面PAD，所以AE⊥AB．因为AB∥CD，所以AE⊥CD．因为AD＝AP，E是PD的中点，所以AE⊥PD．因为CD∩PD＝D，CD，PD⊂平面PCD，所以AE⊥平面PCD．因为MN⊥AB，AB∥CD，所以MN⊥CD．又因为MN⊥PC，PC∩CD＝C，PC，CD⊂平面PCD，所以MN⊥平面PCD，所以AE∥MN．
证明线线平行的常用方法(1)利用线线平行的定义：证共面且无公共点．(2)利用三线平行基本事实4：证两线同时平行于第三条直线．(3)利用线面平行的性质定理：把证线线平行转化为证线面平行．(4)利用线面垂直的性质定理：把证线线平行转化为证线面垂直．(5)利用面面平行的性质定理：把证线线平行转化为证面面平行．
4．如图，在正方体ABCD－A1B1C1D1中，M是AB上一点，N是A1C的中点，MN⊥平面A1DC．求证：MN∥AD1．证明：∵四边形ADD1A1为正方形，∴AD1⊥A1D．∵CD⊥平面ADD1A1，∴CD⊥AD1．∵A1D∩CD＝D，∴AD1⊥平面A1DC．∵MN⊥平面A1DC，∴MN∥AD1．
易错警示　忽略线面垂直判定定理的条件致误　　　　 如图，a∥b，点P在a，b所确定的平面γ外，PA⊥a于点A，AB⊥b于点B．求证：PB⊥b．错解：因为PA⊥a，a∥b，所以PA⊥b．所以PA⊥γ，所以PB⊥b．
易错防范：本题错解的原因在于没有正确使用线面垂直的判定定理，由PA⊥a，PA⊥b，得PA⊥γ，而忽略了“垂直于平面内两条相交直线”这一条件，即a∩b≠∅．正解：因为PA⊥a，a∥b，所以PA⊥b．又因为AB⊥b，PA∩AB＝A，所以b⊥平面PAB．因为PB⊂平面PAB，所以PB⊥b．
| 素 养 达 成 |
1．线线垂直和线面垂直的相互转化：
2．证明线面垂直的方法：(体现直观想象、逻辑推理核心素养)(1)线面垂直的定义．(2)线面垂直的判定定理．(3)如果两条平行直线的一条直线垂直于一个平面，那么另一条直线也垂直于这个平面．(4)如果一条直线垂直于两个平行平面中的一个平面，那么它也垂直于另一个平面．3．线面垂直的性质定理揭示了空间中“平行”与“垂直”关系的内在联系，提供了“垂直”与“平行”关系相互转化的依据．
1．(题型4)在圆柱的一个底面上任取一点(该点不在底面圆周上)，过该点作另一个底面的垂线，则这条垂线与圆柱的母线所在直线的位置关系是(　　)A．相交　B．平行C．异面　D．相交或平行【答案】B【解析】圆柱的母线垂直于圆柱的底面，所作的垂线也垂直于底面，由线面垂直的性质定理可知，二者平行．
2．(多选)(题型1，4)已知m，n为两条不同直线，α，β为两个不同平面，则下列命题正确的有(　　)
【答案】BC【解析】A中n∥α或n在平面α内；D中两直线m，n平行或异面；B，C正确．
4．(题型3)在正方体ABCD－A1B1C1D1中，直线AB1与平面ABCD所成的角等于__________．【答案】45°
【解析】如图所示，因为正方体ABCD－A1B1C1D1中，B1B⊥平面ABCD，所以AB即为AB1在平面ABCD上的射影，∠B1AB即为直线AB1与平面ABCD所成的角．由题意知，∠B1AB＝45°，故所求角为45°．
5．(题型2，4)如图，四棱锥S－ABCD的底面是矩形，SA⊥底面ABCD，E，F分别是SD，SC的中点．求证：(1)BC⊥平面SAB；(2)EF⊥SD．