2022-2023学年河南省驻马店市泌阳县八年级下学期期末数学试题及答案

这是一份2022-2023学年河南省驻马店市泌阳县八年级下学期期末数学试题及答案，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2xy
4x2
a2b2
ab
2x
4x2
3x
x26x9
若分式
A．2
x2的值为 0，则 x的值为（）
x2
B．0C．2
D．2
清华大学从光谱技术领域入手，最终成功破冰芯片新技术，使我们实现了实时超光谱成像芯片的研制，这项技术是全球首例，更加重要的是，其分辨率达到了0.8nm ，数据0.8nm （1m 1000000000nm ）用科学记数法表示为（）
81010m
81010m
0.81010m
8108m
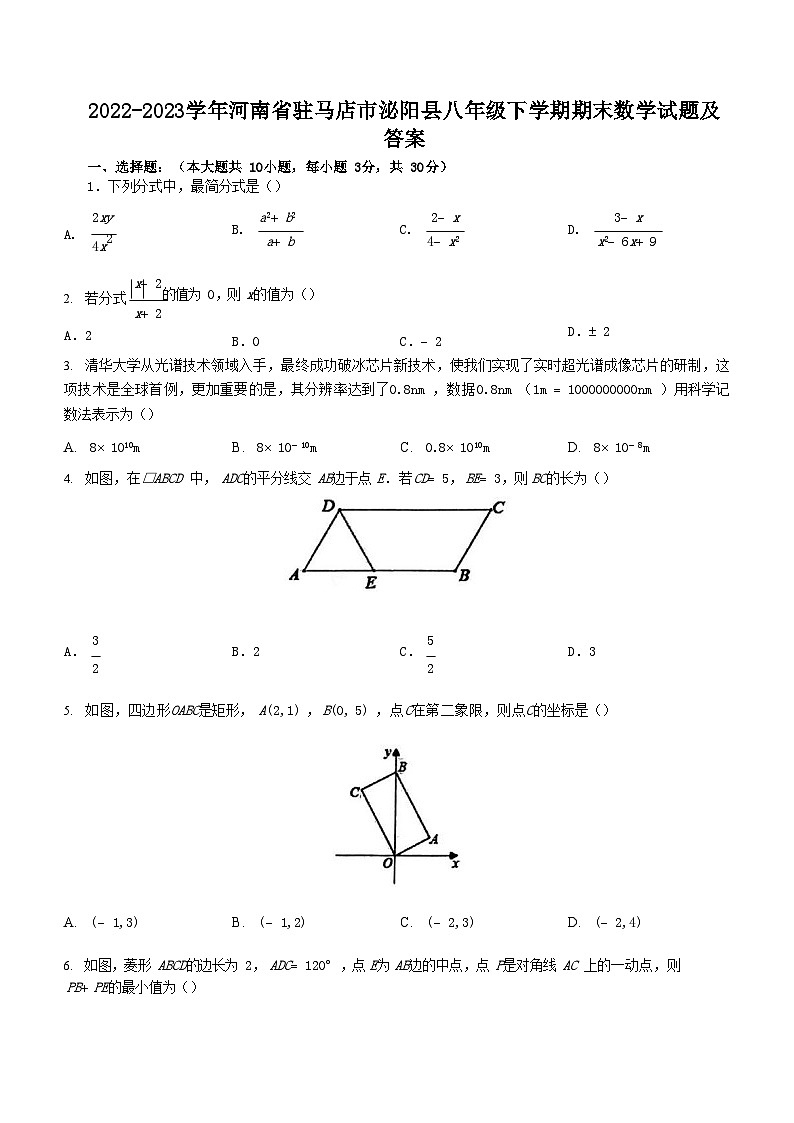
如图，在□ABCD 中， ADC的平分线交 AB边于点 E．若CD5， BE3，则 BC的长为（）
35
A．B．2C．D．3
22
如图，四边形OABC是矩形， A(2,1) ， B(0, 5) ，点C在第二象限，则点C的坐标是（）
(1,3)
(1,2)
(2,3)
(2,4)
如图，菱形 ABCD的边长为 2， ADC120，点 E为 AB边的中点，点 P是对角线 AC 上的一动点，则
PBPE的最小值为（）
2
3
A．B．C．2D．3
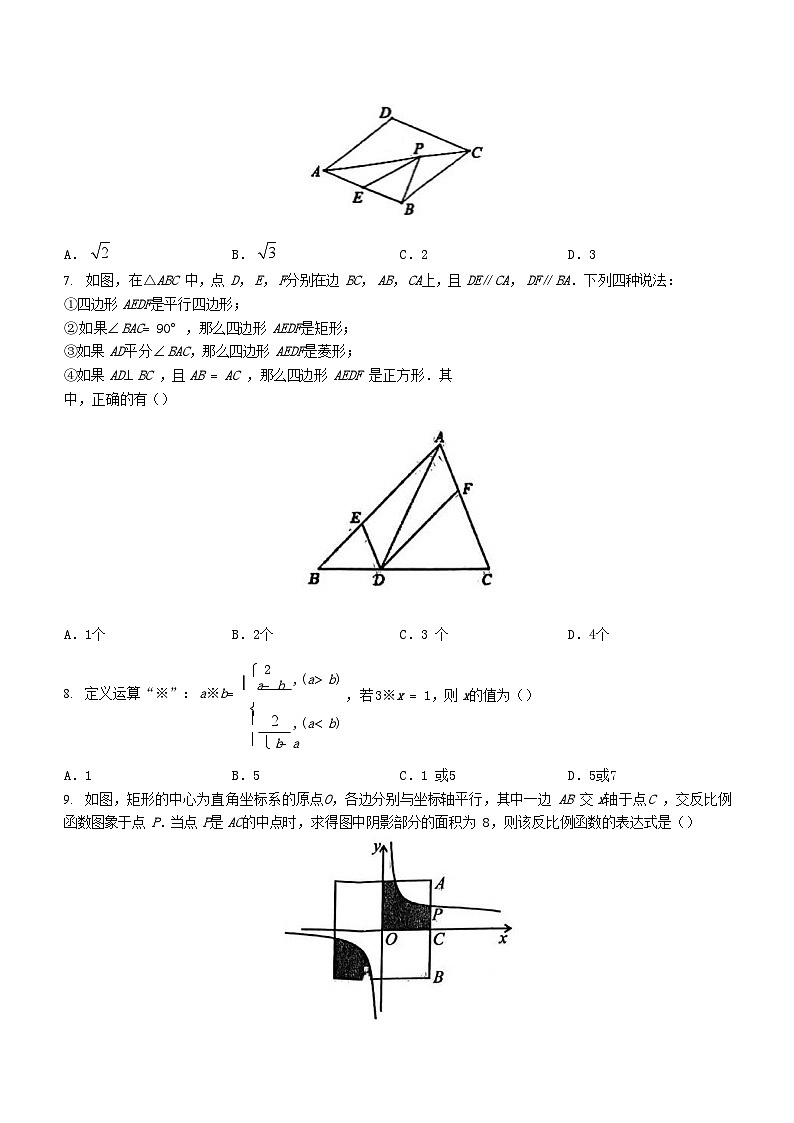
如图，在△ABC 中，点 D， E， F分别在边 BC， AB， CA上，且 DE∥CA， DF∥ BA．下列四种说法：
①四边形 AEDF是平行四边形；
②如果BAC90，那么四边形 AEDF是矩形；
③如果 AD平分BAC，那么四边形 AEDF是菱形；
④如果 ADBC ，且 AB AC ，那么四边形 AEDF 是正方形．其中，正确的有（）
A．1个B．2个C．3 个D．4个
2,(ab)
定义运算“※”： a※bab
，若3※x 1，则 x的值为（）
2

,(ab)
ba
A．1B．5C．1 或5D．5或7
如图，矩形的中心为直角坐标系的原点O，各边分别与坐标轴平行，其中一边 AB 交 x轴于点C ，交反比例函数图象于点 P．当点 P是 AC的中点时，求得图中阴影部分的面积为 8，则该反比例函数的表达式是（）
y2
x
y4
x
y8
x
y16
x
如图，在菱形 ABCD中，分别以C ， D为圆心，大于 1CD长为半径作弧，两弧分别交于点 E、 F，
2
连接 EF，若直线 EF恰好经过点 A，与边CD交于点 M，连接 BM．有以下四个结论：① ABC60，②如
7
果 AB2，那么 BM
，③BC
3CM，④S
1S
；其中正确结论的个数是（）
△ADM
2△ABM
A．4个B．3个C．2 个D．1个
二、填空题：（本大题共 5 小题，每小题 3 分，共 15分）
关于x的分式方程m31有增根，则m的值为．
x22x
mxyn
如图，直线 yx1与直线 ymxn相交于点 M(1, b) ，则关于 x， y的方程组x1y

的解为
平时测验
期中调研
期末调研
成绩
86 分
90 分
105 分
．
小刚在八年级上学期的数学成绩如表所示，若学期总评成绩按图的权重计算，那么小刚该学期的总评成绩是．
如图，矩形 ABCD的对角线 AC， BD相交于点 O， AOB120， CE∥ BD， DE∥ AC．若
AD4，则四边形CODE的周长．
如图在矩形ABCD中，AB8cm，BC6cm，E为CD的中点，动点P从点A出发，以每秒1cm的速度沿ABC运动，最终到达点C，若点P运动的时间为x秒，则当△APE的面积为18cm2时，x值为．
三、解答题（本大题共 8 个小题，共 75 分）
11
4
16．（1）（5分）计算：

(π3)03(1)2023；
（2）（5分）解方程：
3xx2
1
2
．
x2
x22x1x1
17．（8分）先化简，再求值先化简
x21
x1
x1，然后从3x 2的范围内选取一个合适的

整数作为 x的值代入求值．
18．（8分）证明命题“一组对边平行且相等的四边形是平行四边形”，要根据题意，画出图形，并用几何符号表示已知和求证．写出证明过程，下面是小文根据题意画出的图并写出了不完整的已知和求证．
已知：如图，在四边形ABCD 中，AB∥CD ，．求证：．请补全已知和求证部分，并写出证明过程．
19．（9分）为进一步宣传防溺水知识，提高学生防溺水的能力，某校组织七、八年级各 200 名学生进行防溺 水知识竞赛（满分 100 分）．现分别在七、八年级中各随机抽取 10 名学生的测试成绩（单位：分）进行统计、整理如下：
七年级：86，90，79，84，74，93，76，81，90，87．八年级：85，76，90，81，84，92，81，84，83，84．
七八年级测试成绩频数统计表
七八年级测试成绩分析统计表
根据以上信息，解答下列问题：
（1）a，b ，c ；
按学生的实际成绩，你认为哪个年级的学生掌握防溺水知识的总体水平较好？请说明理由．
如果把 x 85的记为“优秀”，把70x 85的记为“合格”，学校规定两项成绩按6 : 4计算．通过计算比较哪个年级得分较高？
20．（10分）某草莓种植基地专门种植草莓并批发出售给超市，草莓的批发总金额 y（元）与批发量 x（斤）是成正比例的函数，比例系数为k ，当 x 10 时， y  250 ．
求y与x的函数关系式为，k的实际意义为；
近日，该基地让利超市：超市一次性批发购进草莓 100斤及以下，不优惠；一次性批发购进草莓 100斤以上，超过 100斤的部分单价打 8折．若某超市每天都从该基地批发购进草莓 x（斤）（x90）并以 35元每斤的价格全部售出，设超市每天销售草莓获得的利润为 w元（不考虑销售过程中的损耗）．
①求 w与 x的函数关系式，并写出 x的取值范围；
②某一天该超市销售草莓的利润为 1900 元，求购进草莓的数量．
21．（8分）紫外线杀菌灯的电阻 y(k) 随温度 x(C) 的变化的大致图象如图所示。通电后温度由室温10C
上升到30C时，电阻与温度成反比的函数关系。且在温度达到30C时，电阻下降到最小值，随后电阻随温
70x80
80x90
90x100
七年级
3
4
3
八年级
1
7
a
平均数
中位数
众数
方差
七年级
84
b
90
36.4
八年级
84
84
c
18.4
度升高而增加，温度每上升1C，电阻增加 4k。
15
当时10x 30时，求 y与 x之间的关系式。
紫外线杀菌灯在使用过程中，温度 x在什么范围内时，电阻不超过6k。
22．（10分） 在菱形 ABCD中， ABC60， 点 P是射线 BD上一动点， 以 AP为边向右侧作等边
△APE，点 E的位置随着点 P的位置变化而变化．
如图1，当点E在菱形ABCD内部或边上时，连接CE，BP与CE的数量关系是；CE与AD
的位置关系是；
如图 2，当点 E在菱形 ABCD外部时，（1）中的结论是否还成立？若成立，请予以证明：若不成立，请说明理由；
如图 3，当点 P在线段 BD的延长线上时，若 AB1， BP3，请直接写出四边形 ACDE的面积．
23．（12分）如图，在平面直角坐标系中，直线 AB： y4x4分别交 x轴、 y轴于点 A、 B，点 P为
3
坐标平面内一点．
将直线AB向下平移5个单位，所得直线的解析式是；
直接写出与直线 AB关于 xx对称的直线的解析式；
若点 P在 x轴上，且APB45，求点 P的坐标；
若点 P在 y 轴上，在坐标平面内是否存在点Q，使以 A、 B、 P、Q为顶点，且以 AB为边的四边形是菱形，若存在，请直接写出点Q的坐标；否则，说明理由．
参考答案及评分标准
一、选择题：每小题 3 分，共 30 分．
1．B2．A3．B4．B5．D6．B7．C8．C9．B10．B
二、填空题：每小题 3 分，共 18 分．
x1

11． m312． y213．98.6分 14．1615．6或 11
三、解答题（本大题共 8 个小题，共 75 分）
16．（1）解：原式41311；
（2）解：方程两边同时乘以(x2)，得到： 3x x22，解得： x 2
经检验， x2是原方程的解，
∴原方程的解是 x2，
(x1)2x1x21
解：原式
(x1)(x1)x1x1

x1x2x
x1
x11，
x1x1
x1
x(x1)x
∵ 3x2，且 x10且 x10且 x0，
∴整数 x2，
当 x2时，原式1．
2
【答案】 AB CD．四边形 ABCD是平行四边形．证明：如图，连接 AC ，
∵AB∥CD，∴BACDCA，
ABCD

在△ABC和△CDA中， BACDCA，

ACCA
∴△ABC≌△CDA(SAS) ，∴ ACB CAD，∴ BC∥ AD ，又∵ AB∥CD ，
∴四边形 ABCD是平行四边形．
【答案】2．85．84．
八年级好些，
七八年级成绩的平均数相等，但八年级成绩的方差小于七年级成绩的方差，成绩比较稳定，所以八年级总体水平较为好些；
七年级得分： (902938786)0.6 (8481797476)0.4425.2（分），八年级得分： (909285) 0.6 (8438128376)0.4 389.4（分），
七年级得分较高．
解：（1）y 25x，草莓每斤的批发价为 25 元；
（2）①当90x100时， w (3525)x10x；
当 x100时，W (3525) 100 (352580%)(x100)
10x(90x100)
即W15x500； w
15x500(x100)
②当90x100时，
x100时， w最大值 1000
∵10001900
∴获利 1900元时， x大于 100
当 w1900时，15x5001900∴ x160
答：购进草莓的数量为 160 斤．
解：（1）当10x30时，设 y与 x之间的关系式为 ym
x
∵图象过点(10, 6)∴ mxy10660
∴10x30时， y与 x的关系式为 y60
x
（2）∵y60
x
当 x30时， y602
30
当 x30时，设 ykxb
∵温度每上升1C，电阻增加 4k∴函数图象过点31, 24
1515


∵函数图象过点(30, 2)∴ 
30kb2,
4
k

解得

4
15．

31kb215,
故当 x30时， y与 x之间的关系式为 y4
15
当 y606时， x10
x
b6
x6
当 y4
15
x66时， x45
答：温度 x的取值范围是10x 45
解：（1）：BPCE， CEAD；
成立， BPCE， CEAD．
证明如下：连接 AC，∵菱形 ABCD中， ABC 60，
∴ABBCCDAD，ADCABC60，
∴△ABC、△ACD是等边三角形，
∴ABAC，ACCD，BAC ACD60，
∵△APE是等边三角形，
∴APAE，PAE60，
∴ BACPACPAEPAC，即BAP CAE ，
∴△BAP≌△CAE(SAS)，∴BPCE，ABPACE
∵ BD平分ABC，∴ ACEABP1ABC30，
2
∴ CE平分ACD，∴ CEAD；
3
（3）
2
解：（1）y4 x1；
3
（2）y4x4；
3
∵直线 AB： y4 x4交 y轴于点 B，
3
∴令 x0，得： y4，∴ B(0, 4)，∴ OB4
∵点 P在 x轴上， APB45，
∴点 P在直线 AB的两侧， OPOB4，
∴ P(4, 0)或(4, 0)；
存在点Q的坐标为(3, 0)或(3, 5) 或(3, 5)