- 专题8.2 空间几何体的表面积和体积(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用) 试卷 0 次下载
- 专题8.3 空间点、直线、平面之间的位置关系(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用) 试卷 0 次下载
- 专题8.5 直线、平面垂直的判定及性质(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用) 试卷 0 次下载
- 专题8.6 几何体与球切、接、截的问题(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用) 试卷 0 次下载
- 专题8.7 空间向量及其运算和空间位置关系(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用) 试卷 0 次下载
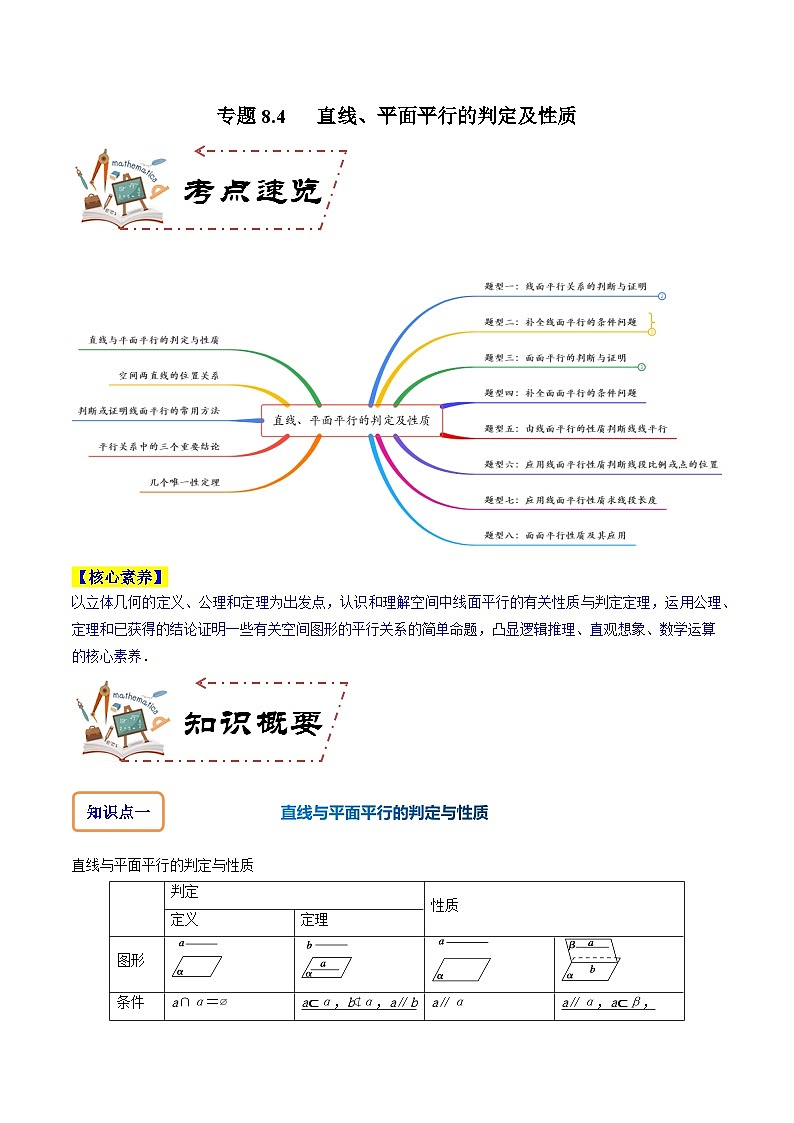
专题8.4 直线、平面平行的判定及性质(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用)
展开【核心素养】
以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理,运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题,凸显逻辑推理、直观想象、数学运算的核心素养.
知识点一
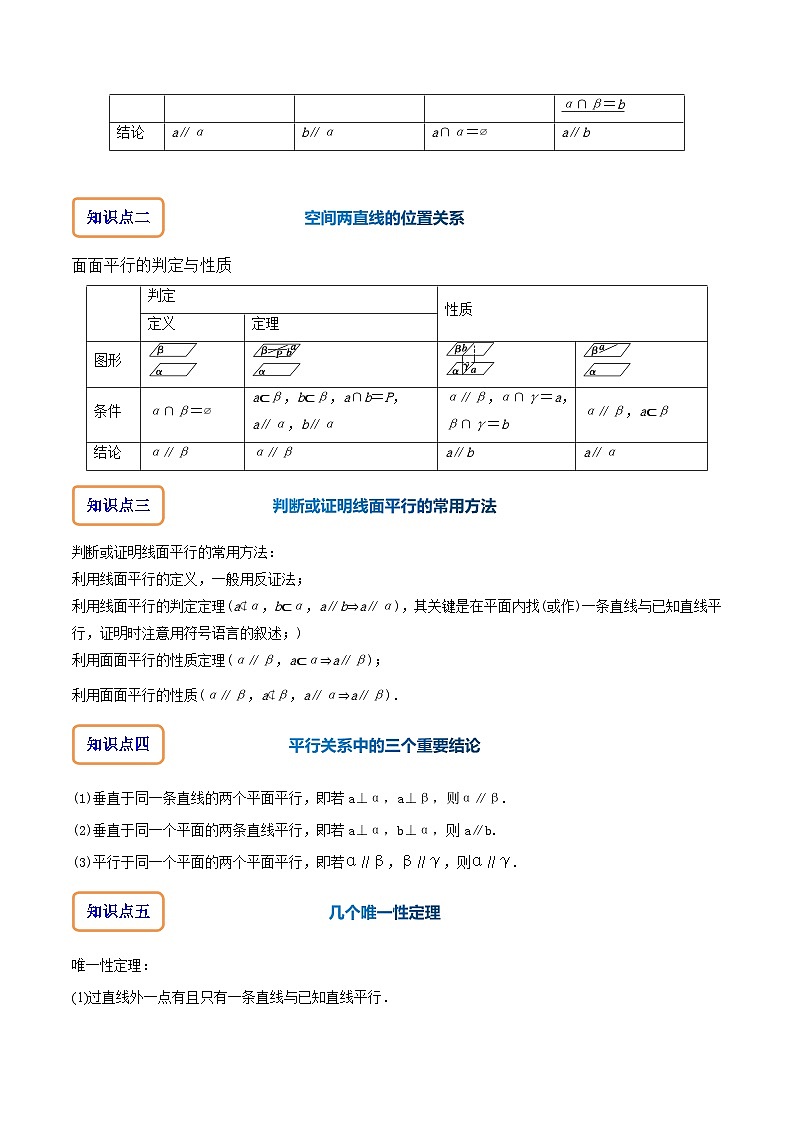
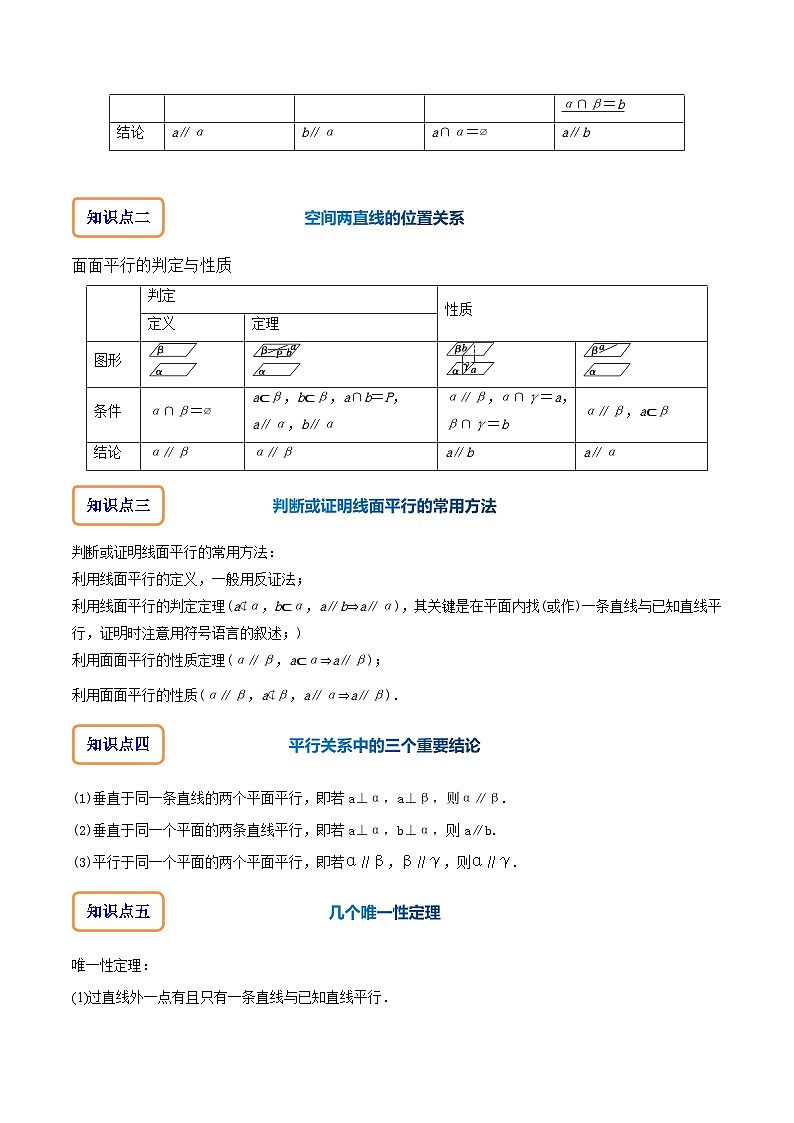
直线与平面平行的判定与性质
直线与平面平行的判定与性质
知识点二
空间两直线的位置关系
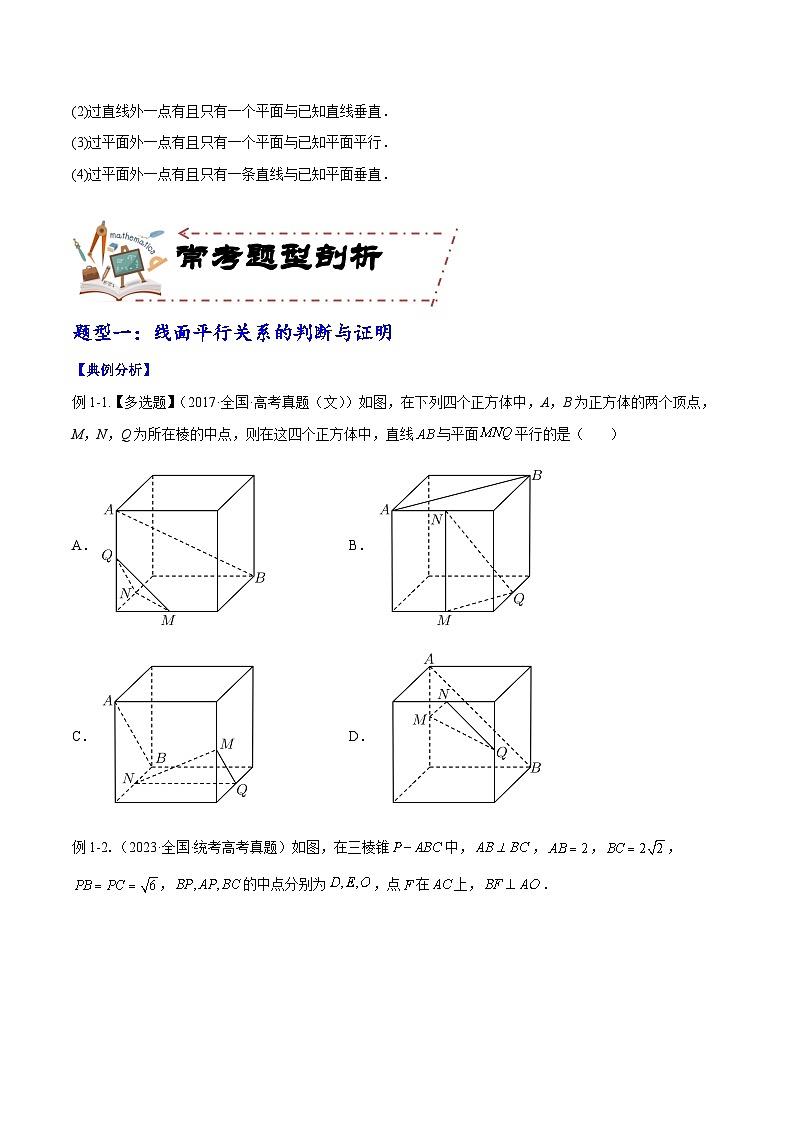
面面平行的判定与性质
知识点三
判断或证明线面平行的常用方法
判断或证明线面平行的常用方法:
利用线面平行的定义,一般用反证法;
利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α),其关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言的叙述;)
利用面面平行的性质定理(α∥β,a⊂α⇒a∥β);
利用面面平行的性质(α∥β,a⊄β,a∥α⇒a∥β).
知识点四
平行关系中的三个重要结论
(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.
(2)垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥b.
(3)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.
知识点五
几个唯一性定理
唯一性定理:
(1)过直线外一点有且只有一条直线与已知直线平行.
(2)过直线外一点有且只有一个平面与已知直线垂直.
(3)过平面外一点有且只有一个平面与已知平面平行.
(4)过平面外一点有且只有一条直线与已知平面垂直.
常考题型剖析
题型一:线面平行关系的判断与证明
【典例分析】
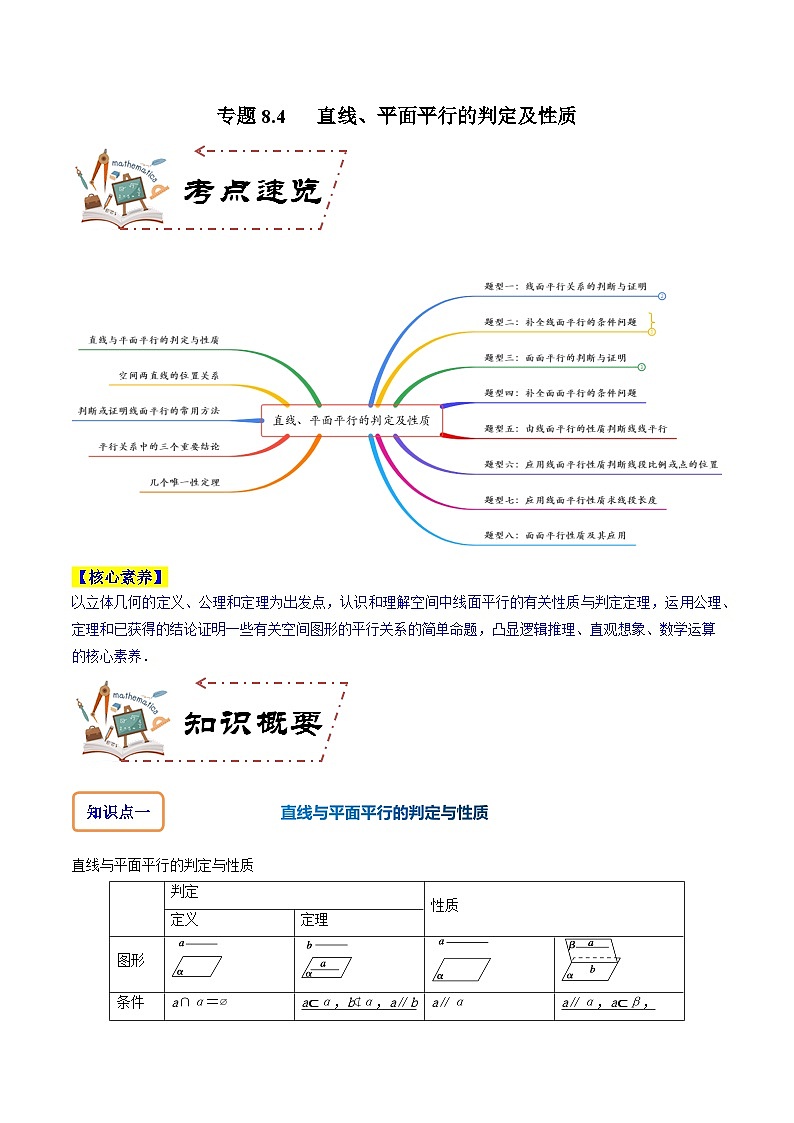
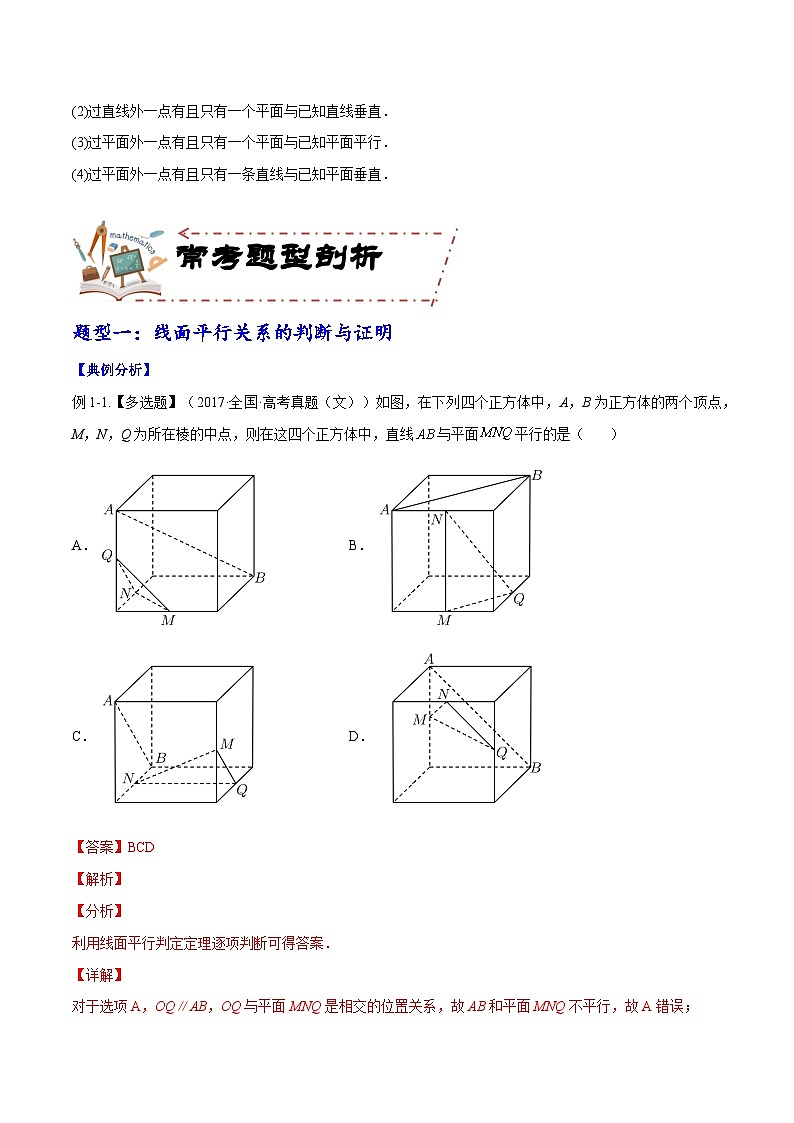
例1-1.【多选题】(2017·全国·高考真题(文))如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线与平面平行的是( )
A.B.
C.D.
例1-2.(2023·全国·统考高考真题)如图,在三棱锥中,,,,,的中点分别为,点在上,.
(1)求证://平面;
(2)若,求三棱锥的体积.
【规律方法】
1.直线、平面间平行的判定方法
(1)关注是否符合判定定理与性质定理,并注意定理中易忽视的条件.
(2)结合题意构造或绘制图形,结合图形作出判断.
(3)利用实物进行空间想象,比较判断.
(4)熟记一些常见结论,如垂直于同一条直线的两个平面平行等.
2.证明直线与平面平行的方法
(1)线面平行的定义:一条直线与一个平面无公共点(不相交).
(2)线面平行的判定定理:关键是找到平面内与已知直线平行的直线.常利用三角形的中位线、平行四边形的对边、成比例线段出现平行线或过已知直线作一平面找其交线.注意内外平行三条件,缺一不可.
【变式训练】
变式1-1.(2022·全国·高三专题练习)如图甲,在梯形ABCD中,,CD=2AB,E、F分别为AD、CD的中点,以AF为折痕把△ADF折起,使点D不落在平面ABCF内(如图乙),那么在以下3个结论中,正确结论的个数是( )
①AF平面BCD;②BE平面CDF;③CD平面BEF.
A.0B.1C.2D.3
变式1-2.(2022秋·新疆伊犁·高三校考阶段练习)如图,在四棱雉中,底面是正方形,,,点,分别为线段,的中点.
(1)求证:平面;
(2)求三棱锥的体积.
题型二:补全线面平行的条件问题
例2-1.(2022·全国·高三专题练习)如图,在四棱锥中,底面为平行四边形,是上一点,当点满足条件: 时,平面.
例2-2.(2021秋·天津红桥·高三天津市复兴中学校考阶段练习)如图所示,在四棱锥中,平面,,E是PD的中点.
(1)求证:;
(2)求证:平面;
(3)若M是线段上一动点,则线段上是否存在点N,使平面?说明理由.
【变式训练】
变式2-1.(2022秋·北京·高三北京市回民学校校考阶段练习)设a,b是两条不同的直线,是平面,,那么“”是“”的( )
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
变式2-2.(2022秋·河南南阳·高三南阳中学校考阶段练习)在三棱锥中,,,、分别是棱、的中点.
(1)证明:;
(2)线段上是否存在点,使得平面?若存在,指出点的位置;若不存在,请说明理由.
题型三:面面平行的判断与证明
【典例分析】
例3-1.(2022秋·广西南宁·高三统考阶段练习)在如图所示的多面体中,平面,,,,点、分别为、的中点.
(1)求证:平面平面;
(2)求多面体的体积.
例3-2.(2022·全国·高三专题练习)如图:在正方体中,为的中点.
(1)求证:平面;
(2)若为的中点,求证:平面平面.
【规律方法】
证明面面平行的常用方法
(1)利用面面平行的定义.
(2)利用面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
(3)利用“垂直于同一条直线的两个平面平行”.
(4)利用“如果两个平面同时平行于第三个平面,那么这两个平面平行”.
(5)利用“线线平行”“线面平行”“面面平行”的相互转化.
【变式训练】
变式3-1.(2022·全国·高三专题练习)如图,在正方体中,是的中点,分别是的中点,求证:
(1)平面;
(2)平面平面.
变式3-2.(陕西·高考真题(文))如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, .
(1)证明: 平面A1BD // 平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
题型四:补全面面平行的条件问题
例4-1.(2022秋·江苏泰州·高三江苏省泰兴中学校联考阶段练习)设是两个不重合的平面,下列选项中,是“”的充要条件的是( )
A.内存在无数条直线与平行B.存在直线与所成的角相等
C.存在平面,满足且D.内存在不共线的三个点到的距离相等
例4-2.(2022·全国·高三专题练习)如图,四棱锥中,,,为的中点.
(1)求证:平面.
(2)在线段上是否存在一点,使得平面平面?若存在,证明你的结论,若不存在,请说明理由.
【变式训练】
变式4-1.(2022·甘肃张掖·高台县第一中学校考模拟预测)设,为不重合的直线,,,为不重合的平面,下列是成立的充分条件的有 (只填序号).
①,
②,,
③,
④,
变式4-2.(2022·全国·高三专题练习)如图,在三棱柱中,,分别为线段,的中点.
(1)求证:平面.
(2)在线段上是否存在一点,使平面平面请说明理由.
题型五:由线面平行的性质判断线线平行
【典例分析】
例5-1.(2023春·全国·高一专题练习)空间四边形中,点为边上的点,且,求证:.
例5-2. (2023春·全国·高一期中)如图所示,已知是平行四边形所在平面外一点,分别是的中点.
(1)求证:平面;
(2)设平面平面,求证:.
【规律方法】
思路方法:
(1)通过线面平行可得到线线平行,其中一条线应是两平面的交线,要树立这种应用意识.
(2)利用线面平行性质必须先找出交线.
2.易错提醒
(1)在推证线面平行时,一定要强调直线不在平面内,否则,会出现错误.
(2)线面平行关系证明的难点在于辅助面和辅助线的添加,在添加辅助线、辅助面时一定要以某一性质定理为依据,绝不能主观臆断.
(3)解题中注意符号语言的规范应用.
【变式训练】
变式5-1.(2023·全国·高三专题练习)如图所示,在三棱柱中,平面与棱交于点,求证:.
变式5-2.(2023春·北京平谷·高一统考期末)三棱锥中,面,、分别是、中点,过的一个平面交面于.
(1)证明:;
(2)证明:.
题型六:应用线面平行性质判断线段比例或点的位置
【典例分析】
例6-1.(2022·全国·高三专题练习)如图、三棱柱的侧棱垂直于底面,是边长为2的正三角形,,点在线段上且,点是线段上的动点.当为多少时,直线平面?
例6-2. (2022秋·黑龙江牡丹江·高三牡丹江一中校考期末)如图,在正方体中,分别是的中点.
(1)证明:平面;
(2)棱上是否存在点,使平面?若存在,求出的值;若不存在,请说明理由.
【变式训练】
变式6-1.(2022·全国·高三专题练习)如图,在四棱锥中,平面底面,底面为平行四边形,.
(1)求证:;
(2)在棱上是否存在点,使得平面?若存在,指出点的位置;若不存在,请说明理由.
变式6-2.(2022·全国·高三专题练习)如图1,菱形中,,,于E,将沿翻折到,使,如图2.
(1)求三棱锥的体积;
(2)在线段上是否存在一点F,使∥平面?若存在,求的值;若不存在,说明理由.
题型七:应用线面平行性质求线段长度
【典例分析】
例7-1.(2022·全国·高三专题练习)在棱长为2的正方体ABCD-A1B1C1D1中,N为BC的中点.当点M在平面DCC1D1内运动时,有MN//平面A1BD则线段MN的最小值为( )
A.1B.C.D.
例7-2.(2022·全国·高三专题练习)在棱长为1的正方体ABCD﹣A1B1C1D1中,点M,N分别是棱BC,CC1的中点,动点P在正方形BCC1B1(包括边界)内运动.若平面AMN,则PA1的最小值是( )
A.1B.C.D.
【变式训练】
变式7-1.(2023·全国·高三专题练习)如图,正方体的棱长为1,E,F是线段上的两个动点, 平面,则的长度为( )
A.B.C.D.2
变式7-2.(2022秋·江西赣州·高三校联考阶段练习)在棱长为4的正方体中,为的中点,点在四边形内(包括边界)运动,若平面,则的最小值为( )
A.B.C.D.
题型八:面面平行性质及其应用
【典例分析】
例8-1.(2022·全国·高三专题练习)如图,已知,,都是平面,且,两条直线l,m分别与平面,,相交于点A,B,C和点D,E,F.已知,,,求AB,BC,EF的长.
例8-2.(2022·全国·高三专题练习)在三棱柱中,
(1)若 分别是的中点,求证:平面平面.
(2)若点分别是上的点,且平面平面,试求的值.
【规律方法】
1.面面平行的应用
(1)两平面平行,构造与之相交的第三个平面,可得交线平行.
(2)两平面平行,其中一个平面内的任意一条直线与另一个平面平行,可用于证明线面平行.
2.三种平行关系之间的转化其中线面平行是核心,线线平行是基础,要注意它们之间的灵活转化.
【变式训练】
变式8-1.(2023·全国·高三专题练习)已知长方体中,,,,分别为棱和的中点,为长方体表面上任意一点.若平面,则的最大值为( )
A.B.C.D.6
变式8-2.(2022·全国·高三专题练习)在三棱柱中,点、分别是、上的点,且平面平面,试求的值.
一、单选题
1.(2022·全国·高三专题练习)如图,正方体的一个截面经过顶点及棱上一点,截面将正方体分成体积比为的两部分,则的值为( )
A.B.C.D.
2.(2022·四川泸州·四川省泸县第四中学校考模拟预测)已知侧棱和底面垂直的三棱柱的所有棱长均为3,为侧棱的中点,为侧棱上一点,且,为上一点,且平面,则的长为( )
A.1B.2C.D.
3.(2022·全国·高三专题练习)如图,在多面体中,平面平面 ,且,则 ( )
A.平面B.平面
C.D.平面平面
二、多选题
4.(2022秋·黑龙江鸡西·高三鸡东县第二中学校考阶段练习)已知分别是三棱锥的棱上的点(不是端点),则下列说法正确的是( )
A.若直线相交,则交点一定在直线上
B.若直线异面,则直线中至少有一条与直线相交
C.若直线异面,则直线中至少有一条与直线平行
D.若直线平行,则直线与直线平行
5.(2022·全国·高三专题练习)如图,正方体的棱长为1,,,分别为线段,,上的动点(不含端点),则( )
A.异面直线与成角可以为
B.当为中点时,存在点,使直线与平面平行
C.当,为中点时,平面截正方体所得的截面面积为
D.存在点,使点与点到平面的距离相等
三、填空题
6.(2022·四川遂宁·统考一模)设和为不重合的两个平面,给出下列命题:
(1)若内的两条相交直线分别平行于内的两条直线,则平行于;
(2)若外一条直线与内一条直线平行,则和平行;
(3)设和相交于直线,若内有一条直线垂直于,则和垂直;
(4)若与内的两条直线垂直,则直线与垂直.
以上说法正确的是 .(㝍出序号)
7.(2022秋·北京·高三北京市八一中学校考阶段练习)如图,在棱长为2的正方体中,M,N分别是线段,的中点,是线段上的动点,过M,N,E的平面截正方体所得的截面面积记为.当为线段的中点时, ;当在线段(包括端点)上运动时,的取值范围是 .
四、解答题
8.(2019·全国卷Ⅰ改编)如图,直四棱柱ABCDA1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.证明:MN∥平面C1DE.
9.(2022·全国·高三专题练习)在如图所示的圆柱中,为圆的直径,、是的两个三等分点,、、都是圆柱的母线.求证:平面;
10.(2023春·江苏连云港·高一校考阶段练习)如图,在五面体ABCDEF中,已知平面ABCD,,,,.
(1)求证:;
(2)求三棱锥的体积.
11.(2022·全国·高三专题练习)如图所示,在四棱锥中,底面为平行四边形,侧面为正三角形,为线段上一点,为的中点.
(1)当为的中点时,求证:平面.
(2)当平面,求出点的位置,说明理由.
12.(2022·四川广安·统考一模)如图,在三棱柱中,侧面为正方形,平面ABC,,,E,F分别为棱AB和的中点.
(1)在棱上是否存在一点D,使得平面EFC?若存在,确定点D的位置,并给出证明;若不存在,试说明理由;
(2)求三棱锥的体积.判定
性质
定义
定理
图形
条件
a∩α=∅
a⊂α,b⊄α,a∥b
a∥α
a∥α,a⊂β,α∩β=b
结论
a∥α
b∥α
a∩α=∅
a∥b
判定
性质
定义
定理
图形
条件
α∩β=∅
a⊂β,b⊂β,a∩b=P,
a∥α,b∥α
α∥β,α∩γ=a,
β∩γ=b
α∥β,a⊂β
结论
α∥β
α∥β
a∥b
a∥α
专题8.3 空间点、直线、平面之间的位置关系(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用): 这是一份专题8.3 空间点、直线、平面之间的位置关系(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用),文件包含专题83空间点直线平面之间的位置关系原卷版docx、专题83空间点直线平面之间的位置关系解析版docx等2份试卷配套教学资源,其中试卷共54页, 欢迎下载使用。
专题7.4 数列求和(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用): 这是一份专题7.4 数列求和(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用),文件包含专题74数列求和原卷版docx、专题74数列求和解析版docx等2份试卷配套教学资源,其中试卷共47页, 欢迎下载使用。
专题6.3 平面向量的应用(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用): 这是一份专题6.3 平面向量的应用(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用),文件包含专题63平面向量的应用原卷版docx、专题63平面向量的应用解析版docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。












