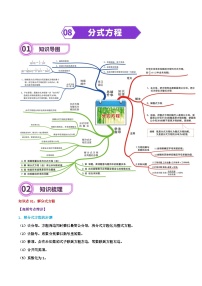
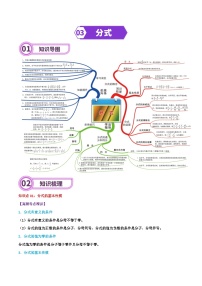
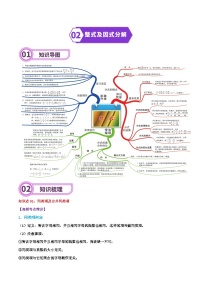
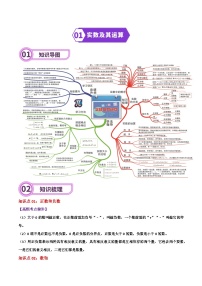
专题14 图形的初步认识-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测)
展开知识点01:几何体的展开图
【高频考点精讲】
1.大多数立体图形是由平面图形围成的,沿着棱剪开就能得到平面图形,这样的平面图形就是相应立体图形的展开图。同一个立体图形按照不同的方式展开,得到的平面展开图是不一样的。
2.正方体的平面展开图
(1)“1-4-1”型,共6种
(2)“1-3-2”型,共3种
(3)“3-3”型,共1种
(4)“2-2-2”型,共1种
3.其他常见几何体的平面展开图
知识点02:展开图还原成几何体
【高频考点精讲】
1.间隔对应:1对3;2对5;4对6
2.“Z”型两端对应:1对4;2对5;3对6
知识点03:方向角
【高频考点精讲】
1.方向角是表示方向的角;以正北、正南方向为基准,来描述物体所处的方向。
2.用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,所以描述方向角时,一般先叙述北或南,再叙述偏东或偏西。注意:四个方向的角平分线按日常习惯描述,即东北,东南,西北,西南。
知识点04:七巧板
【高频考点精讲】
1.七巧板是由5块等腰直角三角形(2块小形三角形、1块中形三角形和2块大形三角形),1块正方形和1块平行四边形组成的。
2.用七块板可以拼搭成三角形、平行四边形、不规则的多角形等几何图形,也可以拼成各种具体的人物形象,动物,中英文字符号等。
3.制作七巧板的方法
(1)在纸上画一个正方形,把它分为十六个小方格;
(2)从左上角到右下角画一条线;
(3)上边的中间与右边的中间连一条线;
(4)从左下角到右上角画一条线,碰到(3)中的线停止;
(5)从刚才那条线的尾端向下画线,碰到(2)中的线停止;
(6)把各个区域涂上不同颜色,沿着线条剪开,皆可以得到一副七巧板。
检测时间:90分钟 试题满分:100分 难度系数:0.50
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2023•巴中)某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“红”的对面是( )
A.传B.承C.文D.化
2.(2分)(2023•连云港)如图,甲是由一条直径、一条弦及一段圆弧所围成的图形;乙是由两条半径与一段圆弧所围成的图形;丙是由不过圆心O的两条线段与一段圆弧所围成的图形.下列叙述正确的是( )
A.只有甲是扇形B.只有乙是扇形
C.只有丙是扇形D.只有乙、丙是扇形
3.(2分)(2023•北京)如图,∠AOC=∠BOD=90°,∠AOD=126°,则∠BOC的大小为( )
A.36°B.44°C.54°D.63°
4.(2分)(2023•宜昌)“争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( )
A.文B.明C.典D.范
5.(2分)(2023•青岛)一个不透明小立方块的六个面上分别标有数字1,2,3,4,5,6,其展开图如图①所示.在一张不透明的桌子上,按图②方式将三个这样的小立方块搭成一个几何体,则该几何体能看得到的面上数字之和最小是( )
A.31B.32C.33D.34
6.(2分)(2023•娄底)一个长方体物体的一顶点所在A、B、C三个面的面积比是3:2:1,如果分别按A、B、C面朝上将此物体放在水平地面上,地面所受的压力产生的压强分别为PA、PB、PC(压强的计算公式为P=),则PA:PB:PC=( )
A.2:3:6B.6:3:2C.1:2:3D.3:2:1
7.(2分)(2023•长春)如图是一个多面体的表面展开图,每个面都标注了数字.若多面体的底面是面③,则多面体的上面是( )
A.面①B.面②C.面⑤D.面⑥
8.(2分)(2023•台湾)如图,直角柱ABCDEF的底面为直角三角形,若∠ABC=∠DEF=90°,BC>AB>BE,则连接 AE后,下列叙述何者正确( )
A.∠ACB<∠FDE,∠AEB>∠ACB
B.∠ACB<∠FDE,∠AEB<∠ACB
C.∠ACB>∠FDE,∠AEB>∠ACB
D.∠ACB>∠FDE,∠AEB<∠ACB
9.(2分)(2023•威海)如图是一正方体的表面展开图.将其折叠成正方体后,与顶点K距离最远的顶点是( )
A.A点B.B点C.C点D.D点
10.(2分)(2023•聊城)如图,该几何体是由一个大圆锥截去上部的小圆锥后剩下的部分.若该几何体上、下两个圆的半径分别为1和2,原大圆锥高的剩余部分OO1为,则其侧面展开图的面积为( )
A.πB.2πC.3πD.4π
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2023•龙川县三模)如果一个角是60°,那么这个角的补角是 °.
12.(2分)(2023•乐山)如图,点O在直线AB上,OD是∠BOC的平分线,若∠AOC=140°,则∠BOD的度数为 .
13.(2分)(2023•三水区模拟)如图,是一个正方体的展开图,那么写有“青”字面的对面上的字是 .
14.(2分)(2023•鼓楼区二模)把如图①所示的正三棱锥沿其中的三条棱剪开后,形成的平面展开图为图②.若剪开的三条棱中有两条是AB、AC,则剪开的另一条棱是 (写出所有正确的答案).
15.(2分)(2023•兰陵县二模)10个棱长为a cm的正方体摆成如图的形状,这个图形的表面积是 .
16.(2分)(2023•余江区二模)七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,如图所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为4的正方形分割制作的七巧板拼摆而成的“叶问蹬”图,则图中抬起的“腿”(即阴影部分)的面积为 .
17.(2分)(2023•无锡)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的表面积为 .
18.(2分)(2023•工业园区一模)一个无盖的长方体包装盒展开后如图所示(单位:cm),则其容积为 cm3.
19.(2分)(2023•开州区校级模拟)如图,已知点O是直线AB上一点,∠1=50°,OF平分∠BOE,则∠2的度数为 .
20.(2分)(2023•丹江口市模拟)如图,将长方形纸片ABCD的一角沿EF折叠,使其落在纸片所在的平面内,点A的对应点为A′,再折叠另一角使B点的对应点B′落在射线EA′上,折痕为EG,那么∠FEG的度数为 .
三.解答题(共8小题,满分60分)
21.(6分)(2023•青县校级模拟)如图,B处在A处的南偏西45°方向上,C处在A处的南偏东30°方向,C处在B处的北偏东60°方向,求∠ACB的度数.
22.(6分)(2023•阳谷县二模)如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行多长时间即可到达.(结果保留根号)
23.(8分)(2023•河南二模)【阅读理解】如图1,小明把一副三角板直角顶点O重叠在一起.如图2固定三角板AOB,将三角板COD绕点O以每秒15°的速度顺时针旋转,旋转时间为t秒,当OD边与OB边重合时停止转动.
【解决问题】
(1)在旋转过程中,请填出∠AOC、∠BOD之间的数量关系 ;
(2)当运动时间为9秒时,图中有角平分线吗?找出并说明理由;
(3)当∠AOC、∠BOD中一个角的度数是另一个角的两倍时,则称射线OC是∠AOB的“优线”,请直接写出所有满足条件的t值.
24.(8分)(2023•雄县一模)某风景区A,B,C,D四个景点在一条直线上,图中数据为各景点之间的距离(单位:千米).
(1)求景点C,D之间的距离.(用含m的代数式表示)
(2)若景点C到景点A的距离与景点C到景点D的距离相等,求景点B,D之间的距离.
25.(8分)(2023•沛县三模)一个无盖的长方体盒子的展开图如图所示.
(1)该盒子的底面的长为 (用含a的式子表示).
(2)若①,②,③,④四个面上分别标有整式2(x+1),x,﹣2,4,且该盒子的相对两个面上的整式的和相等,求x的值.
(3)请在图中补充一个长方形,使该展开图折叠成长方体盒子后有盖.
26.(8分)(2020•枣庄)欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数V(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式: .
27.(8分)(2023•东海县三模)如图所示,一只渔船由西向东沿水平直线行驶,在航线AB的正南方有两个航标C、D.渔船在A处时,测得航标C、D在渔船的南偏东方向分别为30°和60°.渔船航行了6海里到B处时,测得航标C在渔船的南偏西60°方向,而航标D恰好渔船的正南方.求航标C、D之间的距离.
28.(8分)(2021春•东营区校级月考)如图,∠AOB=90°,OP平分∠AOB,OQ平分∠AOC,∠POQ=70°.
(1)求∠AOP的度数;
(2)求∠AOC与∠BOC的度数.
名称
三棱锥
三棱柱
正方体
正八面体
图形
顶点数V
4
6
8
棱数E
6
12
面数F
4
5
8
专题19 命题与证明-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题19 命题与证明-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题19命题与证明教师版docx、专题19命题与证明学生版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
专题18 尺规作图-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题18 尺规作图-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题18尺规作图教师版docx、专题18尺规作图学生版docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。
专题17 圆-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题17 圆-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题17圆教师版docx、专题17圆学生版docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。