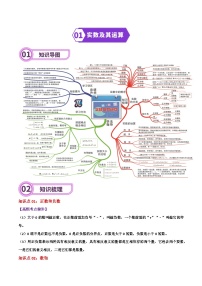
专题15 三角形-2024年中考数学一轮复习重难点精讲练（导图+知识点+新题检测）

这是一份专题15 三角形-2024年中考数学一轮复习重难点精讲练（导图+知识点+新题检测），文件包含专题15三角形教师版docx、专题15三角形学生版docx等2份试卷配套教学资源，其中试卷共46页， 欢迎下载使用。


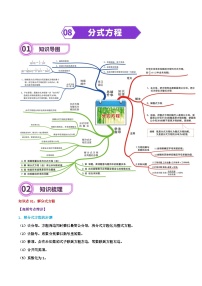
知识点01：三角形的角平分线、中线和高
【高频考点精讲】
1、从三角形的一个顶点向底边作垂线，垂足与顶点之间的线段叫做三角形的高。
2、三角形一个内角的平分线与这个内角的对边交于一点，则这个内角的顶点与交点间的线段叫做三角形的角平分线。
3、三角形一边的中点与此边所对顶点的连线叫做三角形的中线。
4、三角形有3条中线，3条高线，3条角平分线，它们都是线段。
知识点02：三角形的面积
【高频考点精讲】
1、三角形的面积等于底边长与高线乘积的一半，即S△＝×底×高。
2、三角形的中线将三角形分成面积相等的两部分。
知识点03：三角形三边关系
【高频考点精讲】
1、三角形三边关系定理：三角形两边之和大于第三边，三角形的两边差小于第三边。
2、只要两条较短的边长之和大于第三边的长度就可以判定这三条线段能构成一个三角形。
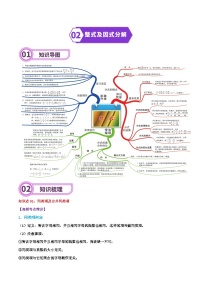
知识点04：三角形内角和定理与外角性质
【高频考点精讲】
1、三角形的内角和等于180°。
2、三角形外角的定义：三角形的一边与另一边的延长线组成的角，叫做三角形的外角。三角形共有六个外角，其中有公共顶点的两个相等。
3、三角形外角的性质
（1）三角形的外角和为360°。
（2）三角形的一个外角等于和它不相邻的两个内角的和。
（3）三角形的一个外角大于和它不相邻的任何一个内角。
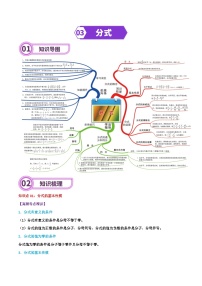
知识点05：全等三角形的判定与性质
【高频考点精讲】
1、三角形全等的判定
（1）三组对应边分别相等的两个三角形全等(SSS)。
（2）有两边及其夹角对应相等的两个三角形全等(SAS)。
（3）有两角及其夹边对应相等的两个三角形全等(ASA)。
（4）有两角及一角的对边对应相等的两个三角形全等(AAS)。
2、全等三角形的性质
（1）全等三角形的对应边相等；全等三角形的对应角相等。
（2）全等三角形的周长、面积相等。
（3）全等三角形的对应边上的高对应相等。
（4）全等三角形的对应角的角平分线相等。
（5）全等三角形的对应边上的中线相等。
知识点06：等腰（等边）三角形的判定与性质
【高频考点精讲】
1、等腰三角形的概念：有两条边相等的三角形叫做等腰三角形。
2、等腰三角形的性质：①等腰三角形的两腰相等；②等腰三角形的两个底角相等（等边对等角）；③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。（三线合一）
3、等边三角形的概念：三条边都相等的三角形叫做等边三角形，等边三角形是特殊的等腰三角形。
4、等边三角形的性质：①等边三角形的三个内角都相等，且都等于60°；②等边三角形是轴对称图形，有3条对称轴；③等边三角形的内角平分线垂直平分对边，三边的垂直平分线是对称轴。
知识点07：三角形中位线定理
【高频考点精讲】
1、三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半。
2、几何语言：如图，∵点D、E分别是AB、AC的中点 ∴DE∥BC，DE＝BC．
检测时间：90分钟 试题满分：100分 难度系数：0.46
一．选择题（共10小题，满分20分，每小题2分）
1．（2分）（2023•绵阳）如图，在等边△ABC中，BD是AC边上的中线，延长BC至点E，使CE＝CD，若DE＝，则AB＝（ ）
A．B．6C．8D．
2．（2分）（2023秋•梅河口市期末）如图，△ABC是等边三角形，D是线段BC上一点（不与点B，C重合），连接AD，点E，F分别在线段AB，AC的延长线上，且DE＝DF＝AD，点D从B运动到C的过程中，△BED周长的变化规律是（ ）
A．不变B．一直变小
C．先变大后变小D．先变小后变大
3．（2分）（2023•台湾）如图，△ABC中，D点在BC上，且BD的中垂线与AB相交于E点，CD的中垂线与AC相交于F点，已知△ABC的三个内角皆不相等，根据图中标示的角，判断下列叙述何者正确（ ）
A．∠1＝∠3，∠2＝∠4B．∠1＝∠3，∠2≠∠4
C．∠1≠∠3，∠2＝∠4D．∠1≠∠3，∠2≠∠4
4．（2分）（2023•株洲）一技术人员用刻度尺（单位：cm）测量某三角形部件的尺寸．如图所示，已知∠ACB＝90°，点D为边AB的中点，点A、B对应的刻度为1、7，则CD＝（ ）
A．3.5cmB．3cmC．4.5cmD．6cm
5．（2分）（2023•宁夏）将一副直角三角板和一把宽度为2cm的直尺按如图方式摆放：先把60°和45°角的顶点及它们的直角边重合，再将此直角边垂直于直尺的上沿，重合的顶点落在直尺下沿上，这两个三角板的斜边分别交直尺上沿于A，B两点，则AB的长是（ ）
A．2﹣B．2﹣2C．2D．2
6．（2分）（2023•浙江）如图，点P是△ABC的重心，点D是边AC的中点，PE∥AC交BC于点E，DF∥BC交EP于点F．若四边形CDFE的面积为6，则△ABC的面积为（ ）
A．12B．14C．18D．24
7．（2分）（2023•河北）四边形ABCD的边长如图所示，对角线AC的长度随四边形形状的改变而变化．当△ABC为等腰三角形时，对角线AC的长为（ ）
A．2B．3C．4D．5
8．（2分）（2023•陕西）如图，DE是△ABC的中位线，点F在DB上，DF＝2BF．连接EF并延长，与CB的延长线相交于点M．若BC＝6，则线段CM的长为（ ）
A．B．7C．D．8
9．（2分）（2023•内蒙古）如图，直线a∥b，直线l与直线a，b分别相交于点A，B，点C在直线b上，且CA＝CB．若∠1＝32°，则∠2的度数为（ ）
A．32°B．58°C．74°D．75°
10．（2分）（2023•菏泽）△ABC的三边长a，b，c满足（a﹣b）2++|c﹣3|＝0，则△ABC是（ ）
A．等腰三角形B．直角三角形
C．锐角三角形D．等腰直角三角形
二．填空题（共10小题，满分20分，每小题2分）
11．（2分）（2023•江西）将含30°角的直角三角板和直尺按如图所示的方式放置，已知∠α＝60°，点B，C表示的刻度分别为1cm，3cm，则线段AB的长为 cm．
12．（2分）（2023•安徽）清初数学家梅文鼎在著作《平三角举要》中，对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明，证明过程中创造性地设计直角三角形，得出了一个结论：如图，AD是锐角△ABC的高，则BD＝（BC+）．当AB＝7，BC＝6，AC＝5时，CD＝ ．
13．（2分）（2023•十堰）一副三角板按如图所示放置，点A在DE上，点F在BC上，若∠EAB＝35°，则∠DFC＝ ．
14．（2分）（2023•重庆）如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D为BC上一点，连接AD．过点B作BE⊥AD于点E，过点C作CF⊥AD交AD的延长线于点F．若BE＝4，CF＝1，则EF的长度为 ．
15．（2分）（2023•台州）如图，点C，D在线段AB上（点C在点A，D之间），分别以AD，BC为边向同侧作等边三角形ADE与等边三角形CBF，边长分别为a，b，CF与DE交于点H，延长AE，BF交于点G，AG长为c．
（1）若四边形EHFG的周长与△CDH的周长相等，则a，b，c之间的等量关系为 ；
（2）若四边形EHFG的面积与△CDH的面积相等，则a，b，c之间的等量关系为 ．
16．（2分）（2023•无锡）《九章算术》中提出了如下问题：今有户不知高、广，竿不知长短，横之不出四尺，从之不出二尺，邪之适出，问户高、广、邪各几何？这段话的意思是：今有门不知其高宽；有竿，不知其长短，横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等．问门高、宽和对角线的长各是多少？则该问题中的门高是 尺．
17．（2分）（2023•扬州）我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成．如图，直角三角形的直角边长为a、b，斜边长为c，若b﹣a＝4，c＝20，则每个直角三角形的面积为 ．
18．（2分）（2023•武汉）如图，DE平分等边△ABC的面积，折叠△BDE得到△FDE，AC分别与DF，EF相交于G，H两点．若DG＝m，EH＝n，用含m，n的式子表示GH的长是 ．
19．（2分）（2023•通辽）如图，等边三角形ABC的边长为6cm，动点P从点A出发以2cm/s的速度沿AB向点B匀速运动，过点P作PQ⊥AB，交边AC于点Q，以PQ为边作等边三角形PQD，使点A，D在PQ异侧，当点D落在BC边上时，点P需移动 s．
20．（2分）（2023•山西）如图，在四边形ABCD中，∠BCD＝90°，对角线AC，BD相交于点O．若AB＝AC＝5，BC＝6，∠ADB＝2∠CBD，则AD的长为 ．
三．解答题（共8小题，满分60分）
21．（6分）（2023•大庆）某建筑物的窗户如图所示，上半部分△ABC是等腰三角形，AB＝AC，AF：BF＝3：4，点G、H、F分别是边AB、AC、BC的中点；下半部分四边形BCDE是矩形，BE∥IJ∥MN∥CD，制造窗户框的材料总长为16米（图中所有黑线的长度和），设BF＝x米，BE＝y米．
（1）求y与x之间的函数关系式，并求出自变量x的取值范围；
（2）当x为多少时，窗户透过的光线最多（窗户的面积最大），并计算窗户的最大面积．
22．（6分）（2023•南通）如图，点D，E分别在AB，AC上，∠ADC＝∠AEB＝90°，BE，CD相交于点O，OB＝OC．
求证：∠1＝∠2．
小虎同学的证明过程如下：
（1）小虎同学的证明过程中，第 步出现错误；
（2）请写出正确的证明过程．
23．（8分）（2023•益阳）如图，AB∥CD，直线MN与AB，CD分别交于点E，F，CD上有一点G且GE＝GF，∠1＝122°，求∠2的度数．
24．（8分）（2023•陕西）如图，在△ABC中，∠B＝50°，∠C＝20°．过点A作AE⊥BC，垂足为E，延长EA至点D．使AD＝AC．在边AC上截取AF＝AB，连接DF．求证：DF＝CB．
25．（8分）（2023•绵阳）如图，在⊙O中，点A，B，C，D为圆周的四等分点，AE为切线，连接ED．并延长交⊙O于点F，连接BF交AC于点G．
（1）求证：AD平分∠CAE；
（2）求证：△ADE≌△ABG；
（3）若AE＝3，AG＝3GC，求cs∠CBF的值．
26．（8分）（2023•临沂）如图，∠A＝90°，AB＝AC，BD⊥AB，BC＝AB+BD．
（1）写出AB与BD的数量关系．
（2）延长BC到E，使CE＝BC，延长DC到F，使CF＝DC，连接EF．求证：EF⊥AB．
（3）在（2）的条件下，作∠ACE的平分线，交AF于点H，求证：AH＝FH．
27．（8分）（2023•宿迁）【问题背景】由光的反射定律知：反射角等于入射角（如图①，即∠CEF＝∠AEF）．小军测量某建筑物高度的方法如下：在地面点E处平放一面镜子，经调整自己位置后，在点D处恰好通过镜子看到建筑物AB的顶端A．经测得，小军的眼睛离地面的距离CD＝1.7m，BE＝20m，DE＝2m，求建筑物AB的高度；
【活动探究】
观察小军的操作后，小明提出了一个测量广告牌高度的做法（如图②）：他让小军站在点D处不动，将镜子移动至E1处，小军恰好通过镜子看到广告牌顶端G，测出DE1＝2m；再将镜子移动至E2处，恰好通过镜子看到广告牌的底端A，测出DE2＝3.4m．经测得，小军的眼睛离地面距离CD＝1.7m，BD＝10m，求这个广告牌AG的高度；
【应用拓展】
小军和小明讨论后，发现用此方法也可测量出斜坡上信号塔AB的高度．他们给出了如下测量步骤（如图③）：①让小军站在斜坡的底端D处不动（小军眼睛离地面距离CD＝1.7m），小明通过移动镜子（镜子平放在坡面上）位置至E处，让小军恰好能看到塔顶B；②测出DE＝2.8m；③测出坡长AD＝17m；④测出坡比为8：15（即）．通过他们给出的方案，请你算出信号塔AB的高度（结果保留整数）．
28．（8分）（2023•河北）如图1和图2，平面上，四边形ABCD中，AB＝8，，CD＝12，DA＝6．∠A＝90°，点M在AD边上，且DM＝2．将线段MA绕点M顺时针旋转n°（0＜n≤180）到MA'，∠A′MA的平分线MP所在直线交折线AB﹣BC于点P，设点P在该折线上运动的路径长为x（x＞0），连接A′P．
（1）若点P在AB上，求证：A'P＝AP；
（2）如图2，连接BD．
①求∠CBD的度数，并直接写出当n＝180时，x的值；
②若点P到BD的距离为2，求tan∠A′MP的值；
（3）当0＜x≤8时，请直接写出点A′到直线AB的距离（用含x的式子表示）．
证明：∵∠ADC＝∠AEB＝90°，
∴∠DOB+∠B＝∠EOC+∠C＝90°．
∵∠DOB＝∠EOC，
∴∠B＝∠C．……第一步
又OA＝OA，OB＝OC，
∴△ABO≌△ACO．……第二步
∴∠1＝∠2．……第三步