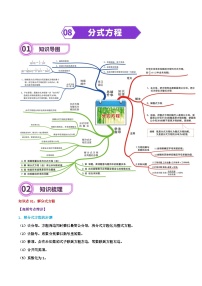
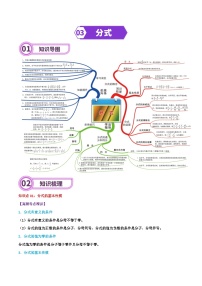
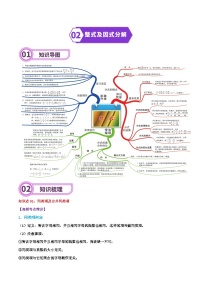
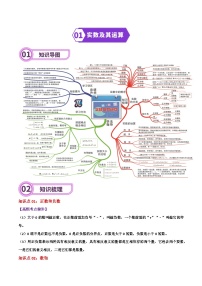
专题17 圆-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测)
展开知识点01:垂径定理及其应用
【高频考点精讲】
1、垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
2、垂径定理的推论
(1)平分弦的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
3、垂径定理的应用:垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题。
知识点02:圆周角定理
【高频考点精讲】
1、圆周角定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
注意:圆周角必须同时满足两个条件:①顶点在圆上;②角的两条边都与圆相交。
2、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
推论:半圆(或直径)所对圆周角是直角,90°的圆周角所对的弦是直径。
3、解题技巧:解决圆的有关问题时,常常需要添加辅助线,构成直径所对的圆周角。
知识点03:圆内接四边形的性质
【高频考点精讲】
1、圆内接四边形的对角互补。
2、圆内接四边形的任意一个外角等于它的内对角。
知识点04:三角形的外接圆与外心
【高频考点精讲】
1、外接圆定义:经过三角形的三个顶点的圆。
2、外心定义:三角形外接圆的圆心是三角形三条边垂直平分线的交点。
3、注意事项
(1)锐角三角形的外心在三角形的内部;直角三角形的外心为直角三角形斜边的中点;钝角三角形的外心在三角形的外部。
(2)找三角形的外心,就是找三角形三条边的垂直平分线的交点,三角形的外接圆只有一个,而一个圆的内接三角形却有无数个。
知识点05:切线的性质
【高频考点精讲】
1、圆的切线垂直于经过切点的半径。
2、经过圆心且垂直于切线的直线必经过切点。
3、经过切点且垂直于切线的直线必经过圆心。
4、切线性质的运用:由切线长定理可知,如果出现圆的切线,可以连接过切点的半径,得出垂直关系。
知识点06:三角形的内切圆与内心
【高频考点精讲】
内切圆定义:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
2、内心定义:三角形三个内角角平分线的交点。
3、任何三角形有且仅有一个内切圆,而任一个圆都有无数个外切三角形。
4、三角形内心的性质
(1)三角形的内心到三角形三边的距离相等。
(2)三角形的内心与三角形顶点的连线平分内角。
知识点07:弧长及扇形面积计算
【高频考点精讲】
1、弧长计算
(1)圆周长公式:C=2πR
(2)弧长公式:l=(弧长为l,圆心角度数为n,圆的半径为R)
2、扇形面积计算
(1)圆面积公式:S=πr2
(2)扇形:组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。
(3)扇形面积计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则
①S扇形=πR2
②S扇形=lR(其中l为扇形的弧长)
(4)求阴影面积解题技巧:将不规则图形面积转化为规则图形的面积。常用方法:①直接用公式法;②和差法;
③割补法。
知识点08:圆锥的计算
【高频考点精讲】
1、圆锥顶点和底面圆周上任意一点的连线叫做圆锥的母线。顶点与底面圆心的连线叫圆锥的高。
2、圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长。
3、圆锥的侧面积:S侧=•2πr•l=πrl.
4、圆锥的全面积:S全=S底+S侧=πr2+πrl
5、圆锥的体积=×底面积×高
6、注意事项
(1)圆锥的母线与展开后所得扇形的半径相等。
(2)圆锥的底面周长与展开后所得扇形的弧长相等。
检测时间:90分钟 试题满分:100分 难度系数:0.50
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2023•湖州)如图,点A,B,C在⊙O上,连结AB,AC,OB,OC.若∠BAC=50°,则∠BOC的度数是( )
A.80°B.90°C.100°D.110°
2.(2分)(2023•锦州)如图,点A,B,C在⊙O上,∠ABC=40°,连接OA,OC.若⊙O的半径为3,则扇形AOC(阴影部分)的面积为( )
A.πB.πC.πD.2π
3.(2分)(2023•赤峰)如图,圆内接四边形ABCD中,∠BCD=105°,连接OB,OC,OD,BD,∠BOC=2∠COD.则∠CBD的度数是( )
A.25°B.30°C.35°D.40°
4.(2分)(2023•广西)如图,点A,B,C,在⊙O上,∠C=40°.则∠AOB的度数是( )
A.50°B.60°C.70°D.80°
5.(2分)(2023•重庆)如图,AB为⊙O的直径,直线CD与⊙O相切于点C,连接AC,若∠ACD=50°,则∠BAC的度数为( )
A.30°B.40°C.50°D.60°
6.(2分)(2023•山西)如图,四边形ABCD内接于⊙O,AC,BD为对角线,BD经过圆心O.若∠BAC=40°,则∠DBC的度数为( )
A.40°B.50°C.60°D.70°
7.(2分)(2023•滨州)如图,某玩具品牌的标志由半径为1cm的三个等圆构成,且三个等圆⊙O1,⊙O2,⊙O3相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A.πcm2B.πcm2C.πcm2D.πcm2
8.(2分)(2023•山西)中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A,B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.5km,则这段圆曲线的长为( )
A.B.C.D.
9.(2分)(2023•河北)如图,点P1~P8是⊙O的八等分点.若△P1P3P7,四边形P3P4P6P7的周长分别为a,b,则下列正确的是( )
A.a<bB.a=b
C.a>bD.a,b大小无法比较
10.(2分)(2023•广元)如图,半径为5的扇形AOB中,∠AOB=90°,C是上一点,CD⊥OA,CE⊥OB,垂足分别为D,E,若CD=CE,则图中阴影部分面积为( )
A.B.C.D.
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2023•青岛)如图,在平面直角坐标系中,已知点A(1,0),P(﹣1,0),⊙P过原点O,且与x轴交于另一点D,AB为⊙P的切线,B为切点,BC是⊙P的直径,则∠BCD的度数为 °.
12.(2分)(2023•南通)如图,AB是⊙O的直径,点C,D在⊙O上,若∠DAB=66°,则∠ACD= 度.
13.(2分)(2023•徐州)如图,在⊙O中,直径AB与弦CD交于点E.=2,连接AD,过点B的切线与AD的延长线交于点F.若∠AFB=68°,则∠DEB= °.
14.(2分)(2023•宁波)如图,圆锥形烟囱帽的底面半径为30cm,母线长为50cm,则烟囱帽的侧面积为 cm2.(结果保留π)
15.(2分)(2023•吉林)如图①,A,B表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点O是圆心,半径r为15m,点A,B是圆上的两点,圆心角∠AOB=120°,则的长为 m.(结果保留π)
16.(2分)(2023•北京)如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC于点D,AE是⊙O的切线,AE交OC的延长线于点E.若∠AOC=45°,BC=2,则线段AE的长为 .
17.(2分)(2023•绍兴)如图,四边形ABCD内接于圆O,若∠D=100°,则∠B的度数是 .
18.(2分)(2023•青海)如图,正方形ABCD的边长是4,分别以点A,B,C,D为圆心,2为半径作圆,则图中阴影部分的面积是 (结果保留π).
19.(2分)(2023•衢州)如图是一个圆形餐盘的正面及其固定支架的截面图,凹槽ABCD是矩形.当餐盘正立且紧靠支架于点A,D时,恰好与BC边相切,则此餐盘的半径等于 cm.
20.(2分)(2023•南充)如图,AB是⊙O的直径,点D,M分别是弦AC,弧AC的中点,AC=12,BC=5,则MD的长是 .
三.解答题(共8小题,满分60分)
21.(6分)(2023•郴州)如图,在⊙O中,AB是直径,点C是圆上一点.在AB的延长线上取一点D,连接CD,使∠BCD=∠A.
(1)求证:直线CD是⊙O的切线;
(2)若∠ACD=120°,CD=2,求图中阴影部分的面积(结果用含π的式子表示).
22.(6分)(2023•北京)如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1)求证DB平分∠ADC,并求∠BAD的大小;
(2)过点C作CF∥AD交AB的延长线于点F,若AC=AD,BF=2,求此圆半径的长.
23.(8分)(2023•内蒙古)如图,AB是⊙O的直径,E为⊙O上的一点,点C是的中点,连接BC,过点C的直线垂直于BE的延长线于点D,交BA的延长线于点P.
(1)求证:PC为⊙O的切线;
(2)若PC=2BO,PB=10,求BE的长.
24.(8分)(2023•娄底)如图1,点G为等边△ABC的重心,点D为BC边的中点,连接GD并延长至点O,使得DO=DG,连接GB,GC,OB,OC.
(1)求证:四边形BOCG为菱形.
(2)如图2,以O点为圆心,OG为半径作⊙O.
①判断直线AB与⊙O的位置关系,并予以证明.
②点M为劣弧BC上一动点(与点B、点C不重合),连接BM并延长交AC于点E,连接CM并延长交AB于点F,求证:AE+AF为定值.
25.(8分)(2023•营口)如图,在△ABC中,AB=BC,以BC为直径作⊙O与AC交于点D,过点D作DE⊥AB,交CB延长线于点F,垂足为点E.
(1)求证:DF为⊙O的切线;
(2)若BE=3,csC=,求BF的长.
26.(8分)(2023•辽宁)如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于点E,过点E作EF∥AB,交CA的延长线于点F.
(1)求证:EF与⊙O相切;
(2)若∠CAB=30°,AB=8,过点E作EG⊥AC于点M,交⊙O于点G,交AB于点N,求的长.
27.(8分)(2023•长春)【感知】如图①,点A、B、P均在⊙O上,∠AOB=90°,则锐角∠APB的大小为 度.
【探究】小明遇到这样一个问题:如图②,⊙O是等边三角形ABC的外接圆,点P在弧AC上(点P不与点A、C重合),连接PA、PB、PC.求证:PB=PA+PC.小明发现,延长PA至点E,使AE=PC,连接BE,通过证明△PBC≌△EBA.可推得△PBE是等边三角形,进而得证.下面是小明的部分证明过程:
证明:延长PA至点E,使AE=PC,连接BE.
∵四边形ABCP是⊙O的内接四边形,
∴∠BAP+∠BCP=180°,
∵∠BAP+∠BAE=180°,
∴∠BCP=∠BAE,
∵△ABC是等边三角形,
∴BA=BC,
∴△PBC≌△EBA(SAS).
请你补全余下的证明过程.
【应用】如图③,⊙O是△ABC的外接圆,∠ABC=90°,AB=BC,点P在⊙O上,且点P与点B在AC的两侧,连接PA、PB、PC,若,则的值为 .
28.(8分)(2023•泰州)已知:A、B为圆上两定点,点C在该圆上,∠C为所对的圆周角.
知识回顾
(1)如图①,⊙O中,B、C位于直线AO异侧,∠AOB+∠C=135°.
①求∠C的度数;
②若⊙O的半径为5,AC=8,求BC的长;
逆向思考
(2)如图②,若P为圆内一点,且∠APB<120°,PA=PB,∠APB=2∠C.求证:P为该圆的圆心;
拓展应用
(3)如图③,在(2)的条件下,若∠APB=90°,点C在⊙P位于直线AP上方部分的圆弧上运动.点D在⊙P上,满足CD=CB﹣CA的所有点D中,必有一个点的位置始终不变.请证明.
专题21 图形的相似-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题21 图形的相似-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题21图形的相似教师版docx、专题21图形的相似学生版docx等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。
专题12 反比例函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题12 反比例函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题12反比例函数教师版docx、专题12反比例函数学生版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
专题11 一次函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题11 一次函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题11一次函数教师版docx、专题11一次函数学生版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。