专题19 命题与证明-2024年中考数学一轮复习重难点精讲练（导图+知识点+新题检测）

这是一份专题19 命题与证明-2024年中考数学一轮复习重难点精讲练（导图+知识点+新题检测），文件包含专题19命题与证明教师版docx、专题19命题与证明学生版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。
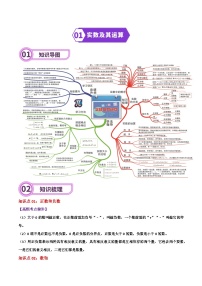
知识点01：命题与推理
【高频考点精讲】
1、判断一件事情的语句，叫做命题。许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项。
2、命题若写成“如果…，那么…”的形式，“如果”后面的部分是题设，“那么”后面的部分是结论。
3、任何一个命题非真即假，说明命题是真命题，需要进行推理论证，而判断命题是假命题，只需举出反例即可。
4、由一个或几个已知的判断（前提），推导出一个未知结论的思维过程，叫做推理。
（1）演绎推理是从一般规律出发，运用逻辑证明或数学运算，得出特殊事实应遵循的规律，即从一般到特殊。
（2）归纳推理是从许多个别事物中概括出一般性概念、原则或结论，即从特殊到一般。
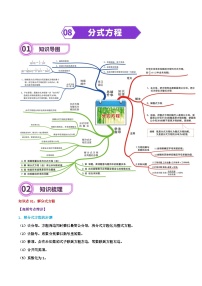
知识点02：反证法
【高频考点精讲】
对于命题，当使用直接证法比较困难时，可以采用间接证法，反证法就是间接证法。
适合类型
（1）命题结论:否定型；（2）命题结论:无限型；（3）命题结论:“至多”或“至少”型。
3、反证法一般步骤
（1）假设命题结论不成立；
（2）从假设出发，经过推理论证，得出矛盾；
（3）由矛盾判定假设不正确，从而肯定原命题结论正确。
检测时间：90分钟 试题满分：100分 难度系数：0.55
一．选择题（共10小题，满分20分，每小题2分）
1．（2分）（2022•绥化）下列命题中是假命题的是（ ）
A．三角形的中位线平行于三角形的第三边，并且等于第三边的一半
B．如果两个角互为邻补角，那么这两个角一定相等
C．从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角
D．直角三角形斜边上的中线等于斜边的一半
2．（2分）（2023•达州）下列命题中，是真命题的是（ ）
A．平行四边形是轴对称图形
B．对角线互相垂直的四边形是菱形
C．到一条线段两个端点距离相等的点，在这条线段的垂直平分线上
D．在△ABC中，若∠A：∠B：∠C＝3：4：5，则△ABC是直角三角形
3．（2分）（2023•内蒙古）下列命题正确的是（ ）
A．“经过有交通信号灯的路口，遇到红灯”是必然事件
B．3.14精确到十分位
C．点（﹣2，﹣3）关于x轴的对称点坐标是（﹣2，3）
D．甲、乙两人参加环保知识竞赛，他们的平均成绩相同，方差分别是S甲2＝2.25，S乙2＝1.81，则甲成绩比乙的稳定
4．（2分）（2023•绥化）下列命题中叙述正确的是（ ）
A．若方差s甲2＞s乙2，则甲组数据的波动较小
B．直线外一点到这条直线的垂线段，叫做点到直线的距离
C．三角形三条中线的交点叫做三角形的内心
D．角的内部到角的两边的距离相等的点在角的平分线上
5．（2分）（2023•衡阳）我们可以用以下推理来证明“在一个三角形中，至少有一个内角小于或等于60°”．假设三角形没有一个内角小于或等于60°，即三个内角都大于60°．”，则三角形的三个内角的和大于180°．这与“三角形的内角和等于180°”这个定理矛盾，所以在一个三角形中，至少有一个内角小于或等于60°．上述推理使用的证明方法是（ ）
A．反证法B．比较法C．综合法D．分析法
6．（2分）（2022•无锡）下列命题中，是真命题的有（ ）
①对角线相等且互相平分的四边形是矩形
②对角线互相垂直的四边形是菱形
③四边相等的四边形是正方形
④四边相等的四边形是菱形
A．①②B．①④C．②③D．③④
7．（2分）（2023•台州）如图，锐角三角形ABC中，AB＝AC，点D，E分别在边AB，AC上，连接BE，CD．下列命题中，假命题是（ ）
A．若CD＝BE，则∠DCB＝∠EBC
B．若∠DCB＝∠EBC，则CD＝BE
C．若BD＝CE，则∠DCB＝∠EBC
D．若∠DCB＝∠EBC，则BD＝CE
8．（2分）（2022•台州）如图，点D在△ABC的边BC上，点P在射线AD上（不与点A，D重合），连接PB，PC．下列命题中，假命题是（ ）
A．若AB＝AC，AD⊥BC，则PB＝PC
B．若PB＝PC，AD⊥BC，则AB＝AC
C．若AB＝AC，∠1＝∠2，则PB＝PC
D．若PB＝PC，∠1＝∠2，则AB＝AC
9．（2分）（2023•无锡）下列命题：①各边相等的多边形是正多边形；②正多边形是中心对称图形；③正六边形的外接圆半径与边长相等；④正n边形共有n条对称轴．其中真命题的个数是（ ）
A．4B．3C．2D．1
10．（2分）（2022•滨州）正方形ABCD的对角线相交于点O（如图1），如果∠BOC绕点O按顺时针方向旋转，其两边分别与边AB、BC相交于点E、F（如图2），连接EF，那么在点E由B到A的过程中，线段EF的中点G经过的路线是（ ）
A．线段B．圆弧C．折线D．波浪线
二．填空题（共10小题，满分20分，每小题2分）
11．（2分）（2022•宜昌）如图，点A，B，C都在方格纸的格点上，△ABC绕点A顺时针方向旋转90°后得到△AB'C'，则点B运动的路径的长为 ．
12．（2分）（2023•盐城）如图，在Rt△ABC中，∠ACB＝90°，∠B＝60°，BC＝3，将△ABC绕点C逆时针旋转到△EDC的位置，点B的对应点D首次落在斜边AB上，则点A的运动路径的长为 ．
13．（2分）（2022•德州）如图，△ABC是等腰直角三角形，∠ACB＝90°，AC＝BC＝4，点D是斜边AB上一点，且BD＝AB，将△ABC绕点D逆时针旋转90°，得到△A′B′C′，B′C′交AB于点E．其中点C的运动路径为弧CC′，则弧CC′的长度为 ．
14．（2分）（2023•北京）学校组织学生参加木艺艺术品加工劳动实践活动．已知某木艺艺术品加工完成共需A，B、C，D、E，F、G七道工序，加工要求如下：
①工序C，D须在工序A完成后进行，工序E须在工序B，D都完成后进行，工序F须在工序C，D都完成后进行；
②一道工序只能由一名学生完成，此工序完成后该学生才能进行其他工序；
③各道工序所需时间如下表所示：
在不考虑其他因素的前提下，若由一名学生单独完成此木艺艺术品的加工，则需要 分钟；若由两名学生合作完成此木艺艺术品的加工，则最少需要 分钟．
15．（2分）（2023•海南）如图，在正方形ABCD中，AB＝8，点E在边AD上，且AD＝4AE，点P为边AB上的动点，连接PE，过点E作EF⊥PE，交射线BC于点F，则＝ .若点M是线段EF的中点，则当点P从点A运动到点B时，点M运动的路径长为 ．
16．（2分）（2023•郴州）如图，在Rt△ABC中，∠BAC＝90°，AB＝3cm，∠B＝60°．将△ABC绕点A逆时针旋转，得到△AB'C'，若点B的对应点B'恰好落在线段BC上，则点C的运动路径长是 cm（结果用含π的式子表示）．
17．（2分）（2022•福建）推理是数学的基本思维方式，若推理过程不严谨，则推理结果可能产生错误．
例如，有人声称可以证明“任意一个实数都等于0”，并证明如下：
设任意一个实数为x，令x＝m，
等式两边都乘以x，得x2＝mx．①
等式两边都减m2，得x2﹣m2＝mx﹣m2．②
等式两边分别分解因式，得（x+m）（x﹣m）＝m（x﹣m）．③
等式两边都除以x﹣m，得x+m＝m．④
等式两边都减m，得x＝0．⑤
所以任意一个实数都等于0．
以上推理过程中，开始出现错误的那一步对应的序号是 ．
18．（2分）（2022•通辽）如图，⊙O是△ABC的外接圆，AC为直径，若AB＝2，BC＝3，点P从B点出发，在△ABC内运动且始终保持∠CBP＝∠BAP，当C，P两点距离最小时，动点P的运动路径长为 ．
19．（2分）（2022•内蒙古）如图，在等腰直角三角形ABC中，AC＝BC＝1，点P在以斜边AB为直径的半圆上，M为PC的中点，当点P沿半圆从点A运动至点B时，点M运动的路径长是 ．
20．（2分）（2022•广元）如图，直尺AB垂直竖立在水平面上，将一个含45°角的直角三角板CDE的斜边DE靠在直尺的一边AB上，使点E与点A重合，DE＝12cm．当点D沿DA方向滑动时，点E同时从点A出发沿射线AF方向滑动．当点D滑动到点A时，点C运动的路径长为 cm．
三．解答题（共8小题，满分60分）
21．（6分）（2023•泰州）如图，CD是五边形ABCDE的一边，若AM垂直平分CD，垂足为M，且 ， ，则 ．
给出下列信息：①AM平分∠BAE；②AB＝AE；③BC＝DE．请从中选择适当信息，将对应的序号填到横线上方，使之构成真命题，补全图形，并加以证明．
22．（6分）（2023•建湖县三模）请在①AE＝CF；②AB＝CD；③AB∥CD这三个条件中任选一个补充在下面题目的横线上使之成为真命题，并解答出后面的问题．
（1）已知，如图，四边形BEDF是平行四边形，点A、C在对角线EF所在的直线上， （填写序号）．求证：△ABE≌△CDF；
（2）连接AD、BC，若AC平分∠BAD，已知AB＝10，AC＝16．求四边形ABCD的面积．
23．（8分）（2023•吉安模拟）课本再现：（1）定理 直角三角形斜边上的中线等于斜边的一半．已知：如图1，在Rt△ABC中，∠ACB＝90°，CD是AB边上的中线．
求证：CD＝AB．
证明：如图1，延长CD到点E，使得DE＝CD，连接BE，AE，
…
请把证明过程补充完整．
知识应用：（2）如图2，在△ABC中，AD是边BC上的高，CE是边AB上的中线，F是CE的中点，连接DF并延长交AC于点G，连接GE，AB＝2CD．求证：EG＝CG．
24．（8分）（2023•许昌二模）如图，△ABC内接于⊙O，AB是⊙O的直径，过点C作⊙O的切线，交BA的延长线于点P，点F在PC上，连接AF，OF．
易证命题：“若AF是⊙O的切线，则OF∥BC”是真命题．
（1）请写出该命题的逆命题 ．
（2）判断（1）中的命题是否为真命题，并说明理由；
（3）若⊙O的半径为4，AF＝3，且OF∥BC，求AC的长．
25．（8分）（2023•吉安县校级模拟）一抽纸纸筒被安装在竖直墙面上，图1是其侧面示意图，其中AB⊥BC，AB∥CE∥DF，AD∥EF∥BC，纸筒盖CMP可以绕着点C旋转，关闭时点P与点F重合，CM⊥PM，AB＝30cm，DF＝6cm，CM＝EF＝7cm．
（1）若∠BCM＝150°，求纸筒盖关闭时点P运动的路径长；
（2）如图2，当一卷底面直径为10cm的圆柱体纸巾恰好能放入纸筒内时，求纸筒盖要打开的最小角∠PCF的度数．（参考数据：sin11.，cs78.，，cs73.
26．（8分）（2023•靖江市校级三模）如图，在⊙O中，AB是弦，半径OE⊥AB于点F，点C为⊙O外一点，连接AC、BC，连接AE并延长交BC于点D，给出下列信息：①AC与⊙O相切于点A；②AB＝AC；③点D是BC的中点．
（1）请在上述3条信息中选择其中两条作为条件，剩下的一条作为结论构成一个真命题．你选择的条件是 ， ，结论是 （只要填写序号）．完成你的证明；
（2）在（1）的条件下，若已知：AD＝4，sin∠DAC＝，求⊙O的半径．
27．（8分）（2023•南山区三模）（1）如图，直线AB经过⊙O上一点C，连接OA、OB，从以下三个信息中选择两个作为条件，剩余的一个作为结论组成一个真命题，并写出你的证明过程．①OA＝OB；②CA＝CB；③AB是⊙O的切线．你选择的条件是 ，结论是 （填序号）；
（2）在（1）的条件下，若∠AOB＝90°，，求图中阴影部分的面积．
28．（8分）（2023•鼓楼区二模）在学习矩形的判定时，王老师提出一个命题：“一组对边相等，一组对角相等且另外两个角中有一个直角的四边形是矩形”．小明和小丽都发现这个命题是假命题，并举出了反例．
（1）小明：如图①，Rt△ABC中，∠C＝90°，把△ABC沿AB翻折，得到△ABD，再以D为圆心，DB长为半径作弧，交射线CB于点E，连接DE，过点A、E分别作AC、BC的垂线，交于点F．则四边形AFED是该命题的一个反例．
请你说明此反例的合理性．
（2）小丽：作出图②，在△ABC中，∠B＝90°，∠NMB＝∠A．她发现四边形ABMN已满足一组对角相等，一个角是直角，但无法保证MN恰好与AB相等，请你完善小丽的作法，并在图②的基础上用尺规作图作出符合要求的M′N′，使四边形ABM′N′是该命题的一个反例（保留作图的痕迹，写出必要的文字说明）．
工序
A
B
C
D
E
F
G
所需时间/分钟
9
9
7
9
7
10
2