专题20 图形的变换与坐标-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测)
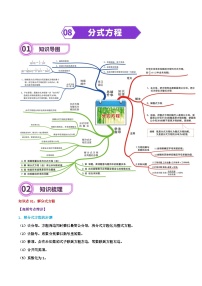
展开知识点01:轴对称变换
【高频考点精讲】
1、轴对称图形
把一个图形沿一条直线折叠,直线两边的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,折叠后重合的对应点,叫做对称点。常见的轴对称图形:等腰三角形,矩形,正方形,等腰梯形,圆等。
2、轴对称性质
(1)关于直线对称的两个图形是全等图形。
(2)对称轴是对应点连线的垂直平分线。
(3)如果两个图形的对应点连线被同一直线垂直平分,那么这两个图形关于这条直线对称。
3、关于x轴、y轴对称的点的坐标
(1)关于x轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数,即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y);
(2)关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变,即点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y)。
4、最短路线问题
在直线l上方有两个点A、B,确定直线l上到A、B的距离之和最短的点,可以通过轴对称来确定,即作出其中一点关于直线l的对称点,对称点与另一点的连线与直线l的交点即为所求。
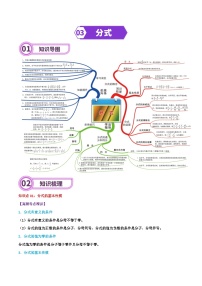
知识点02:平移变换
【高频考点精讲】
1、把一个图形整体沿某一直线方向移动一定的距离,得到一个新的图形,图形的这种移动,叫做平移。
2、平移的两个要素:(1)图形平移的方向;(2)图形平移的距离。
3、平移性质:对应点所连线段平行且相等。
4、平移变换与坐标变化
(1)坐标点P(x,y)向右平移a个单位,得出P(x+a,y);
(2)坐标点P(x,y)向左平移a个单位,得出P(x﹣a,y);
(3)坐标点P(x,y)向上平移b个单位,得出P(x,y+b);
(4)坐标点P(x,y)向下平移b个单位,得出P(x,y﹣b)。
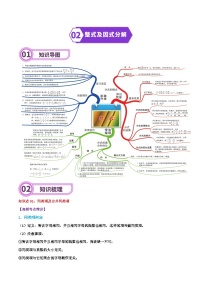
知识点03:旋转变换
【高频考点精讲】
1、将一个图形绕一个定点沿某个方向转动一定的角度,这样的图形变换叫做旋转,这个定点叫做旋转中心,转动的角度叫做旋转角。
2、旋转性质
(1)对应点到旋转中心的距离相等.
(2)对应点与旋转中心所连线段的夹角等于旋转角。
(3)旋转前后的图形全等。
3、旋转作图
根据对应角相等且等于旋转角,对应线段相等,由此可以通过作相等的角,在角的边上截取相等线段的方法,找到对应点,顺次连接得出旋转后的图形。
检测时间:90分钟 试题满分:100分 难度系数:0.47
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2023•常州)在平面直角坐标系中,若点P的坐标为(2,1),则点P关于y轴对称的点的坐标为( )
A.(﹣2,﹣1)B.(2,﹣1)C.(﹣2,1)D.(2,1)
解:点P的坐标是(2,1),则点P关于y轴对称的点的坐标是(﹣2,1),
故选:C.
2.(2分)(2023•临沂)某小区的圆形花园中间有两条互相垂直的小路,园丁在花园中栽种了8棵桂花,如图所示.若A,B两处桂花的位置关于小路对称,在分别以两条小路为x,y轴的平面直角坐标系内,若点A的坐标为(﹣6,2),则点B的坐标为( )
A.(6,2)B.(﹣6,﹣2)C.(2,6)D.(2,﹣6)
解:若A,B两处桂花的位置关于小路对称,在分别以两条小路为x,y轴的平面直角坐标系内,若点A的坐标为(﹣6,2),则点B的坐标为(6,2).
故选:A.
3.(2分)(2023•郴州)下列图形中,能由图形a通过平移得到的是( )
A.B.
C.D.
解:由平移定义得,平移只改变图形的位置,
观察图形可知,选项B中图形是由图形a通过平移得到,
A,C,D均不能由图形a通过平移得到,
故选:B.
4.(2分)(2023•黄石)如图,已知点A(1,0),B(4,m),若将线段AB平移至CD,其中点C(﹣2,1),D(a,n),则m﹣n的值为( )
A.﹣3B.﹣1C.1D.3
解:∵线段CD由线段AB平移得到,
且A(1,0),C(﹣2,1),B(4,m),D(a,n),
∴m﹣n=0﹣1=﹣1.
故选:B.
5.(2分)(2022•福建)如图,现有一把直尺和一块三角尺,其中∠ABC=90°,∠CAB=60°,AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到△A′B′C′,点A′对应直尺的刻度为0,则四边形ACC′A′的面积是( )
A.96B.96C.192D.160
解:在Rt△ABC中,∠CAB=60°,AB=8,
则BC=AB•tan∠CAB=8,
由平移的性质可知:AC=A′C′,AC∥A′C′,
∴四边形ACC′A′为平行四边形,
∵点A对应直尺的刻度为12,点A′对应直尺的刻度为0,
∴AA′=12,
∴S四边形ACC′A′=12×8=96,
故选:B.
6.(2分)(2023•无锡)如图,△ABC中,∠BAC=55°,将△ABC逆时针旋转α(0°<α<55°),得到△ADE,DE交AC于F.当α=40°时,点D恰好落在BC上,此时∠AFE等于( )
A.80°B.85°C.90°D.95°
解:∵将△ABC逆时针旋转α(0°<α<55°),得到△ADE,
∴∠BAC=∠DAE,∠BAD=∠CAE=40°,AB=AD,∠C=∠E,
∴∠B=70°,
∴∠C=∠E=55°,
∴∠AFE=180°﹣55°﹣40°=85°,
故选:B.
7.(2分)(2023•德州)如图,△ABC绕点A逆时针旋转一定角度后得到△ADE,点D在BC上,∠EDC=40°,则∠B的度数为( )
A.70°B.60°C.50°D.40°
解:设AC交DE于点F,
∵∠AFD=∠E+∠EAC,∠AFD=∠C+∠EDC,
∴∠E+∠EAC=∠C+∠EDC,
由旋转得∠E=∠C,∠DAB=∠EAC,AD=AB,
∴∠EAC=∠EDC=40°,∠ADB=∠B,
∴∠DAB=∠EAC=40°,
∵∠ADB+∠B+∠DAB=180°,
∴∠B+∠B+40°=180°,
∴∠B=70°,
故选:A.
8.(2分)(2023•天津)如图,把△ABC以点A为中心逆时针旋转得到△ADE,点B,C的对应点分别是点D,E,且点E在BC的延长线上,连接BD,则下列结论一定正确的是( )
A.∠CAE=∠BEDB.AB=AEC.∠ACE=∠ADED.CE=BD
解:如图,设AD与BE的交点为O,
∵把△ABC以点A为中心逆时针旋转得到△ADE,
∴∠ABC=∠ADE,∠BAD=∠CAE,
又∵∠AOB=∠DOE,
∴∠BED=∠BAD=∠CAE,
故选:A.
9.(2分)(2023•金华)如图,两盏灯笼的位置A,B的坐标分别是(﹣3,3),(1,2),将点B向右平移2个单位,再向上平移1个单位得到点B′,则关于点A,B′的位置描述正确的是( )
A.关于x轴对称B.关于y轴对称
C.关于原点O对称D.关于直线y=x对称
解:∵点B′由点B(1,2)向右平移2个单位,再向上平移1个单位得到
∴此时B′坐标为(3,3).
∴A与B′关于y轴对称.
故选:B.
10.(2分)(2023•海南)如图,在平面直角坐标系中,点A在y轴上,点B的坐标为(6,0),将△ABO绕着点B顺时针旋转60°,得到△DBC,则点C的坐标是( )
A.(3,3)B.(3,3)C.(6,3)D.(3,6)
解:作CM⊥x轴于M,
∵点B的坐标为(6,0),
∴BC=OB=6,
∵∠OBC=60°,
∴BM=,CM==3,
∴OM=OB﹣BM=6﹣3=3,
∴C(3,3).
故选:B.
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2023•金昌)如图1,我国是世界上最早制造使用水车的国家.1556年兰州人段续的第一架水车创制成功后,黄河两岸人民纷纷仿制,车水灌田,水渠纵横,沃土繁丰.而今,兰州水车博览园是百里黄河风情线上的标志性景观,是兰州“水车之都”的象征.如图2是水车舀水灌溉示意图,水车轮的辐条(圆的半径)OA长约为6米,辐条尽头装有刮板,刮板间安装有等距斜挂的长方体形状的水斗,当水流冲动水车轮刮板时,驱使水车徐徐转动,水斗依次舀满河水在点A处离开水面,逆时针旋转150°上升至轮子上方B处,斗口开始翻转向下,将水倾入木槽,由木槽导入水渠,进而灌溉,那么水斗从A处(舀水)转动到B处(倒水)所经过的路程是 5π 米.(结果保留π)
解:=(米).
故答案为:5π.
12.(2分)(2022•临沂)如图,在平面直角坐标系中,△ABC的顶点A,B的坐标分别是A(0,2),B(2,﹣1).平移△ABC得到△A'B'C',若点A的对应点A'的坐标为(﹣1,0),则点B的对应点B'的坐标是 (1,﹣3) .
解:由题意知,点A从(0,2)平移至(﹣1,0),可看作是△ABC先向下平移2个单位,再向左平移1个单位(或者先向左平移1个单位,再向下平移2个单位),
即B点(2,﹣1),平移后的对应点为B'(1,﹣3),
故答案为:(1,﹣3).
13.(2分)(2023•滨州)如图,在平面直角坐标系中,△ABO的三个顶点坐标分别为A(6,3),B(6,0),O(0,0),若将△ABO向左平移3个单位长度得到△CDE,则点A的对应点C的坐标是 (3,3) .
解:∵A(6,3)向左平移3个单位长度得到C,
∴点A的对应点C的坐标是(6﹣3,3),即(3,3).
故答案为:(3,3).
14.(2分)(2023•济南)如图,将菱形纸片ABCD沿过点C的直线折叠,使点D落在射线CA上的点E处,折痕CP交AD于点P.若∠ABC=30°,AP=2,则PE的长等于 + .
解:过点A作AF⊥PE于点F,
∵四边形ABCD是菱形,
∴∠D=∠ABC=30°,AD=CD,
∴∠DAC==75°,
由折叠可知:∠E=∠D=30°,
∴∠APE=∠DAC﹣∠AEP=45°,
在Rt△APF中,PF=AP•cs∠APE,
∴PF=AF=2×cs45°=,
在Rt△AEF中,tan∠AEP=,
∴EF===,
∴PE=PF+EF=+,
故答案为:+.
15.(2分)(2023•张家界)如图,AO为∠BAC的平分线,且∠BAC=50°,将四边形ABOC绕点A逆时针方向旋转后,得到四边形AB′O′C′,且∠OAC′=100°,则四边形ABOC旋转的角度是 75° .
解:∵AO为∠BAC的平分线,∠BAC=50°,
∴∠BAO=∠CAO=∠BAC=25°,
依据旋转的性质可知∠C′AO′=∠CAO=25°,旋转角为∠OAO′,
∴∠OAO′=∠OAC′﹣∠C′AO′=100°﹣25°=75°.
故答案为:75°.
16.(2分)(2023•淄博)在边长为1的正方形网格中,右边的“小鱼”图案是由左边的图案经过一次平移得到的,则平移的距离是 6 .
解:右边的“小鱼”图案是由左边的图案经过一次平移得到的,则平移的距离是6,
故答案为:6.
17.(2分)(2023•襄阳)如图,在△ABC中,AB=AC,点D是AC的中点,将BCD沿BD折叠得到△BED,连接AE.若DE⊥AB于点F,BC=10,则AF的长为 2 .
解:取BC中点H,连接AH,过点D作DG⊥BC于点G,DM⊥BE于点M.
设EF=a,AD=CD=DE=x,则DF=x﹣a.
∵AB=AC,
∴AB=2x,∠ABC=∠ACB,BH=HC=5.
又由折叠得∠ACB=∠BED,BE=BC=10,
∴∠ABC=∠BED,
∴cs∠ABC=cs∠BED,即 =,
∴=,
解得:a=,
∴DF=x﹣a=x﹣,
∵D 是AC中点,DG⊥BC,
∴DG是△AHC的中位线,
∴CG=CH=,
∴BG=,
由折叠知∠DEM=∠DCG,ED=CD,
在△EMD和△CGD中,
,
∴△EMD≌△CGD(AAS),
∴DG=MD.
∵DE⊥AB,
∴∠EFB=90°,
∴∠DEB+∠EBF=90°.
又∵∠CAH+∠ACB=90°,且∠ACB=∠DEB,
∴∠EBF=∠CAH,
∴∠EBF+∠ABC=90°,
∴∠DMB=∠MBG=∠BGD=90°
∴四边形 MBGD是正方形,
∴DG=BG=,
∴AH=2DG=15.
在 Rt△AHC中,AH2+HC2=AC2,
∴152+52=(2x)2,
解得:x=,
∴a=,x﹣a=,即AD=,DF=,
在 Rt△AFD中,AF==2.
18.(2分)(2023•宜宾)如图,M是正方形ABCD边CD的中点,P是正方形内一点,连接BP,线段BP以B为中心逆时针旋转90°得到线段BQ,连接MQ.若AB=4,MP=1,则MQ的最小值为 2﹣1 .
解:连接BM,将△BCM绕B逆时针旋转90°得△BEF,连接MF,QF,如图:
∵∠CBE=90°,∠ABC=90°,
∴∠ABC+∠CBE=180°,
∴A,B,E共线,
∵∠PBM=∠PBQ﹣∠MBQ=90°﹣∠MBQ=∠FBQ,
由旋转性质得PB=QB,MB=FB,
∴△BPM≌△BQF(SAS),
∴MP=QF=1,
∴Q的运动轨迹是以F为圆心,1为半径的弧,
∵BC=AB=4,CM=CD=2,
∴BM==2,
∵∠MBF=90°,BM=BF,
∴MF=BM=2,
∵MQ≥MF﹣QF,
∴MQ≥2﹣1,
∴MQ的最小值为2﹣1.
故答案为:2﹣1.
19.(2分)(2023•泰州)如图,△ABC中,AB=AC,∠A=30°,射线CP从射线CA开始绕点C逆时针旋转α角(0°<α<75°),与射线AB相交于点D,将△ACD沿射线CP翻折至△A′CD处,射线CA′与射线AB相交于点E.若△A′DE是等腰三角形,则∠α的度数为 22.5°或67.5°或45° .
解:由折叠得:∠ACD=∠A′CD=α=∠ACA′,∠A=∠DA′C=30°,
分三种情况:
当A′D=A′E时,如图:
∴∠A′DE=∠A′ED=(180°﹣∠A′)=75°,
∵∠A′ED是△ACE的一个外角,
∴∠ACE=∠A′ED﹣∠A=45°,
∴∠ACD=∠A′CD=α=∠ACE=22.5°;
当A′D=A′E时,当△ADC和△A′DC位于射线AB的同侧时,如图:
∴∠A′DE=∠A′ED=∠CA′D=15°,
∴∠ACA′=180°﹣∠A﹣∠A′EA=135°,
∴∠ACD=∠A′CD=α=∠ACA′=67.5°;
当DA′=DE时,
∴∠A′=∠DEA′=30°,
∵∠DEA′是△ACE的一个外角,
∴∠DEA′>30°,
∴此种情况不成立;
当ED=EA′时,如图:
∴∠EDA′=∠A′=30°,
∴∠DEA′=180°﹣∠EDA′﹣∠A′=120°,
∵∠A′ED是△ACE的一个外角,
∴∠ACE=∠A′ED﹣∠A=90°,
∴∠ACD=∠A′CD=α=∠ACE=45°;
综上所述:若△A′DE是等腰三角形,则∠α的度数为22.5°或67.5°或45°,
故答案为:22.5°或67.5°或45°.
20.(2分)(2022•毕节市)如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点A1(1,1);把点A1向上平移2个单位,再向左平移2个单位,得到点A2(﹣1,3);把点A2向下平移3个单位,再向左平移3个单位,得到点A3(﹣4,0);把点A3向下平移4个单位,再向右平移4个单位,得到点A4(0,﹣4),…;按此做法进行下去,则点A10的坐标为 (﹣1,11) .
解:由图象可知,A5(5,1),
将点A5向左平移6个单位、再向上平移6个单位,可得A6(﹣1,7),
将点A6向左平移7个单位,再向下平移7个单位,可得A7(﹣8,0),
将点A7向右平移8个单位,再向下平移8个单位,可得A8(0,﹣8),
将点A8向右平移9个单位,再向上平移9个单位,可得A9(9,1),
将点A9向左平移10个单位,再向上平移10个单位,可得A10(﹣1,11),
故答案为:(﹣1,11).
三.解答题(共8小题,满分60分)
21.(6分)(2023•安徽)如图,在由边长为1个单位长度的小正方形组成的网格中,点A,B,C,D均为格点(网格线的交点).
(1)画出线段AB关于直线CD对称的线段A1B1;
(2)将线段AB向左平移2个单位长度,再向上平移1个单位长度,得到线段A2B2,画出线段A2B2;
(3)描出线段AB上的点M及直线CD上的点N,使得直线MN垂直平分AB.
解:(1)线段A1B1如图所示;
(2)线段A2B2如图所示;
(3)直线MN即为所求.
22.(6分)(2023•宿迁)如图,在▱ABCD中,AB=5,,∠A=45°.
(1)求出对角线BD的长;
(2)尺规作图:将四边形ABCD沿着经过A点的某条直线翻折,使点B落在CD边上的点E处,请作出折痕.(不写作法,保留作图痕迹)
解:(1)如图所示,连接BD,过D作DH⊥AB于H,
∵∠A=45°,∠AHD=90°,
∴∠ADH=45°=∠A,
∴△ADH是等腰直角三角形,
又∵,
∴AH=DH=3,
∴BH=AB﹣AH=5﹣3=2,
∴Rt△BDH中,BD==;
(2)如图所示,AG即为所求.
23.(8分)(2023•黑龙江)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2),C(3,﹣3).
(1)将△ABC向上平移4个单位,再向右平移1个单位,得到△A1B1C1,请画出△A1B1C1;
(2)请画出△ABC关于y轴对称的△A2B2C2;
(3)将△A2B2C2绕着原点O顺时针旋转90°,得到△A3B3C3,求线段A2C2在旋转过程中扫过的面积(结果保留π).
解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)将△A2B2C2绕着原点O顺时针旋转90°,得到△A3B3C3,如图,连接OC3交于D,连接OC2交于E,
∵A2(﹣2,﹣1),B2(﹣1,﹣2),C2(﹣3,﹣3),
∴OA2==,OB2==,OC2==3,
∴OA2=OB2=OD=OE=,
由旋转得:OA2=OA3,OB2=OB3,OC2=OC3,A2C2=A3C3,∠C2OC3=∠DOE=90°,
∴△OA2C2≌△OA3C3(SSS),
∴=,
∴线段A2C2在旋转过程中扫过的面积=S﹣S扇形DOE=﹣=.
24.(8分)(2021•温州)如图中4×4与6×6的方格都是由边长为1的小正方形组成.图1是绘成的七巧板图案,它由7个图形组成,请按以下要求选择其中一个并在图2、图3中画出相应的格点图形(顶点均在格点上).
(1)选一个四边形画在图2中,使点P为它的一个顶点,并画出将它向右平移3个单位后所得的图形.
(2)选一个合适的三角形,将它的各边长扩大到原来的倍,画在图3中.
解:(1)如图2所示,即为所求;
(2)如图3所示,即为所求.
25.(8分)(2023•宁波)在4×4的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
(1)在图1中先画出一个以格点P为顶点的等腰三角形PAB,再画出该三角形向右平移2个单位后的△P′A′B′.
(2)将图2中的格点△ABC绕点C按顺时针方向旋转90°,画出经旋转后的△A′B′C.
解:(1)如图1,△P′A′B′即为所求;
(2)如图2,△A′B′C即为所求.
26.(8分)(2023•甘孜州)如图,在Rt△ABC中,,点D在AB边上,连接CD,将CD绕点C逆时针旋转90°得到CE,连接BE,DE.
(1)求证:△CAD≌△CBE;
(2)若AD=2时,求CE的长;
(3)点D在AB上运动时,试探究AD2+BD2的值是否存在最小值,如果存在,求出这个最小值;如果不存在,请说明理由.
(1)证明:由题意,可知∠ACB=∠DCE=90°,CA=CB,CD=CE.
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB.
即∠ACD=∠BCE.
在△CAD和△CBE中,
∴△CAD≌△CBE(SAS);
(2)解:∵在 Rt△ABC中,,
∴∠CAB=∠CBA=45°,,
∴BD=AB﹣AD=6﹣2=4.
∵△CAD≌△CBE(SAS),
∴BE=AD=2,∠CBE=∠CAD=45°,
∴∠ABE=∠ABC+∠CBE=90°.
∴,
∴在 Rt△CDE 中,;
(3)解:存在,理由:
由(2)可知,AD2+BD2=BE2+BD2=DE2=2CD2,
∴当CD最小时,有 AD2+BD2 的值最小,此时 CD⊥AB.
∵△ABC 为等腰直角三角形,
∴,
∴AD2+BD2=2CD2≥2×32=18.
即 AD2+BD2 的最小值为18.
27.(8分)(2023•大连)综合与实践
问题情境
数学活动课上,老师发给每名同学一个等腰三角形纸片ABC,AB=AC,∠BAC>90°,要求同学们将纸片沿一条直线折叠,探究图形中的结论.
问题发现
奋进小组在边AC上取一点D,连接BD,将这个纸片沿BD翻折,点A的对应点为E,如图1所示.
如图2,小明发现,当点E落在边BC上时,∠DEC=2∠ACB.
如图3,小红发现,当点D是AC的中点时,连接CE,若已知AB和CE的长,则可求BD的长.
……
问题提出与解决
奋进小组根据小明和小红的发现,讨论后提出问题1,请你解答.
问题1:在△ABC中,AB=AC,∠BAC>90°,点D是边AC上一点,将△ABD沿BD翻折得到△EBD.
(1)如图2,当点E在边BC上时,求证:∠DEC=2∠ACB.
(2)如图3,当点D是AC的中点时,连接CE,若AB=4,CE=3,求BD的长.
拓展延伸
小刚受到探究过程的启发,将等腰三角形的顶角改为锐角,尝试画图,并提出问题2,请你解答.
问题2:如图4,点D是△ABC外一点,AB=AC=BD=4,CD=1,∠ABD=2∠BDC,求BC的长.
问题1,
(1)证明:∵将△ABD沿BD翻折得到△EBD,
∴∠BED=∠A,
∵∠BED+∠DEC=180°,
∴∠A+∠DEC=180°,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠A+∠ACB+∠ABC=∠A+2∠ACB=180°,
∴∠DEC=2∠ACB;
(2)解:如图1,
作AG⊥BD于G,作DF⊥CE于F,
∴∠AGD=∠DFC=90°,
由折叠得,
AD=DE,∠ADB=∠BDE,
∵点D是AC的中点,
∴CD=AD,
∴DE=CD,
∴∠DEC=∠DCE,CF=EF=CE=
∴DF2=CD2﹣CF2=22﹣()2=,
∵∠ADB+∠BDE+∠EDC=180°,
∴2∠ADB+∠EDC=180°,
∵∠DEC+∠DCE+∠EDC=180°,
∴2∠DCE+∠EDC=180°,
∴∠ADB=∠DCE,
∴△ADG≌△DFC(AAS),
∴AG=DF,DG=CF=,
在Rt△ABG中,由勾股定理得,
BG==,
∴BD=BG+DG=;
问题2,
解:如图2,
连接AD,作BE⊥AD于E,作BF⊥CD,交DC的延长线于F,
∵AB=BD,
∴∠ABD=2∠DBE,DE=AE=AD,
∵∠ABD=2∠BDC,
∴∠BDE=∠BDC,
∴CD∥BE,
∴CD⊥AD,
∴∠BED=∠EDC=∠F=90°,
∴四边形DEBF是矩形,
∴BF=DE,DF=BE,
在Rt△ACD中,CD=1,AC=4,
∴AD==,
∴BF=DE=,
在Rt△BDE中,BD=4,DE=,
∴DF=BE==,
∴CF=DF﹣CD=,
在Rt△BCF中,CF=,BF=,
∴BC==.
28.(8分)(2023•贵州)如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B,点P在CB上.
(1)【动手操作】
如图②,若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形,图中∠PBE的度数为 135 度;
(2)【问题探究】
根据(1)所画图形,探究线段PA与PE的数量关系,并说明理由;
(3)【拓展延伸】
如图③,若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD交于点E,探究线段BA,BP,BE之间的数量关系,并说明理由.
解:(1)画出图形如下:
∵CA=CB,∠C=90°,
∴∠ABC=45°,
∵BD⊥AB,
∴∠ABD=90°,
∴∠PBE=∠ABC+∠ABD=45°+90°=135°;
故答案为:135;
(2)PA=PE,理由如下:
过P作PM∥AB交AC于M,如图:
∴∠MPC=∠ABC=45°,
∴△PCM是等腰直角三角形,
∴CP=CM,∠PMC=45°,
∴CA﹣CM=CB﹣CP,即AM=BP,∠AMP=135°=∠PBE,
∵∠APE=90°,
∴∠EPB=90°﹣∠APC=∠PAC,
∴△APM≌△PEB(ASA),
∴PA=PE;
(3)当P在线段BC上时,过P作PM∥AB交AC于M,如图:
由(2)可知,BE=PM,BP=AM,
∵AB=(AM+CM),
∴AB=BP+CM,
∵PM=CM,
∴AB=BP+BE;
当P在线段CB的延长线上时,过P作PN⊥BC交BE于N,如图:
∵∠ABD=90°,∠ABC=45°,
∴∠PBN=180°﹣∠ABC﹣∠ABD=45°,
∴△BPN是等腰直角三角形,∠ABP=135°,
∴BP=NP,BN=BP,∠PNB=45°,
∴∠PNE=135°=∠ABP,
∵∠APE=90°,
∴∠EPN=90°﹣∠APN=∠APB,
∴△EPN≌△APB(ASA),
∴EN=BA,
∵BE=EN+BN,
∴BE=BA+BP;
综上所述,当P在线段BC上时,AB=BP+BE;当P在线段CB的延长线上时,BE=BA+BP
专题21 图形的相似-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题21 图形的相似-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题21图形的相似教师版docx、专题21图形的相似学生版docx等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。
专题12 反比例函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题12 反比例函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题12反比例函数教师版docx、专题12反比例函数学生版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
专题13 二次函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测): 这是一份专题13 二次函数-2024年中考数学一轮复习重难点精讲练(导图+知识点+新题检测),文件包含专题13二次函数教师版docx、专题13二次函数学生版docx等2份试卷配套教学资源,其中试卷共48页, 欢迎下载使用。