天津市河东区2022-2023学年七年级（上）期末数学试卷(含答案 人教版)

这是一份天津市河东区2022-2023学年七年级（上）期末数学试卷(含答案 人教版)，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）如果水位下降2021m记作﹣2021m，那么水位上升2020m记作（ ）
A．﹣1mB．4041mC．﹣4041mD．2020m
2．（3分）下列说法中正确的是（ ）
A．整数一定是正数
B．有这样的有理数，它既不是正数，也不是负数
C．零是最小的整数
D．有这样的有理数，它既是正数，也是负数
3．（3分）若|a|＝4，|b|＝1，a与b异号，则a﹣b的值为（ ）
A．3B．5
C．±3D．±5
4．（3分）下列式子中a，﹣xy2，，0，是单项式的有（ ）个．
A．2B．3
C．4D．5
5．（3分）联合国报告显示，新冠肺炎疫情可能导致全球饥饿人数大幅增加．去年全世界有8.28亿人处于饥饿状态，828000000用科学记数法表示为（ ）
A．8.28×107B．8.28×108C．8.28×109D．8.28×1010
6．（3分）若3a2bn﹣1与是同类项，则mn的值为（ ）
A．3B．2
C．1D．0
7．（3分）解方程＝x﹣时，去分母正确的是（ ）
A．3（x+1）＝x﹣（5x﹣1）
B．3（x+1）＝12x﹣5x﹣1
C．3（x+1）＝12x﹣（5x﹣1）
D．3x+1＝12x﹣5x+1
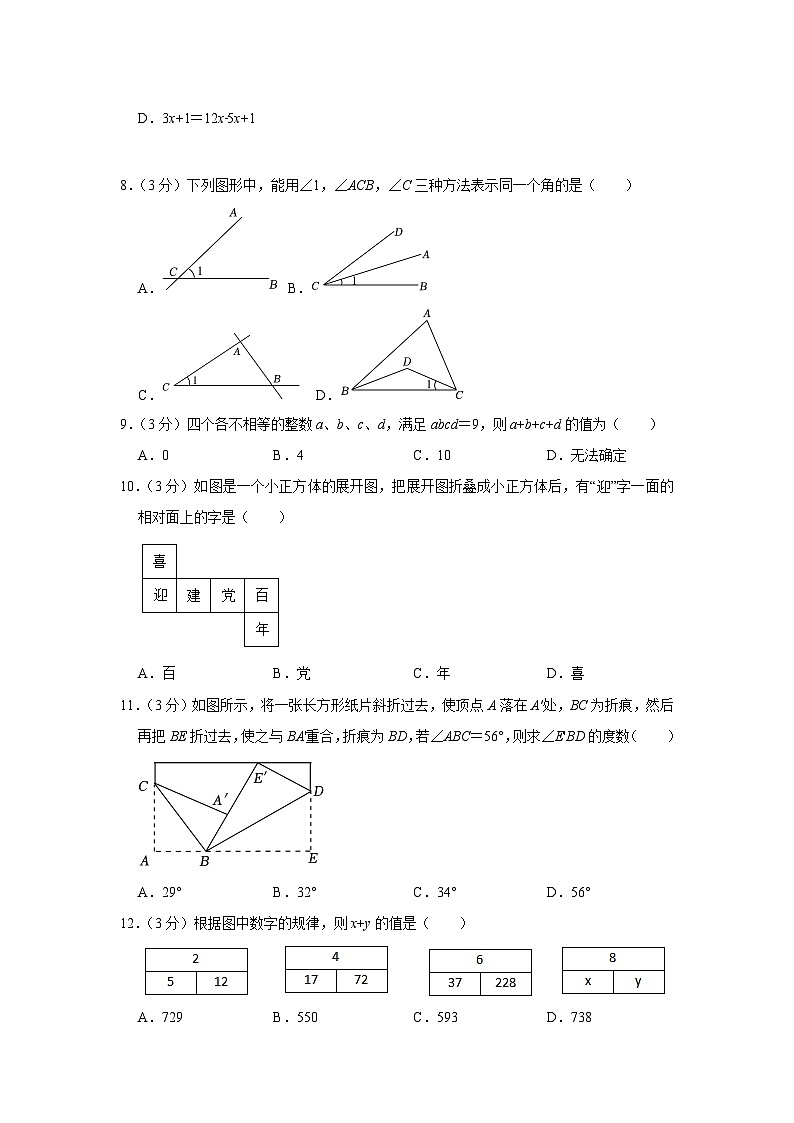
8．（3分）下列图形中，能用∠1，∠ACB，∠C三种方法表示同一个角的是（ ）
A．B．
C．D．
9．（3分）四个各不相等的整数a、b、c、d，满足abcd＝9，则a+b+c+d的值为（ ）
A．0B．4C．10D．无法确定
10．（3分）如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“迎”字一面的相对面上的字是（ ）
A．百B．党C．年D．喜
11．（3分）如图所示，将一张长方形纸片斜折过去，使顶点A落在A′处，BC为折痕，然后再把BE折过去，使之与BA'重合，折痕为BD，若∠ABC＝56°，则求∠E'BD的度数（ ）
A．29°B．32°C．34°D．56°
12．（3分）根据图中数字的规律，则x+y的值是（ ）
A．729B．550C．593D．738
二、填空题：（每题3分，共18分）
13．（3分）单项式πr3的系数是 ．
14．（3分）方程3x﹣2（x+3）＝6的解是 ．
15．（3分）在△ABC中，已知∠A＝60°，∠ABC的平分线与∠ACB的平分线相交于点O，则∠BOC的度数为 ．
16．（3分）如图，AB＝16cm，C是AB上一点，且AC＝10cm，D是AC的中点，E是BC的中点，则线段DE的长度为 cm．
17．（3分）已知互余的两个角的差为20°，则这两个角的度数分别为 ．
18．（3分）在﹣1，2，﹣3，0，5这五个数中，任取两个相除，其中商最小的是 ．
三、解答题：（共7道大题，共46分）
19．（6分）（1）24×；
（2）﹣14+（﹣2）3÷4×[5﹣（﹣3）2]．
20．（6分）先化简，再求值：3（2x2﹣xy）﹣4（﹣6+xy+x2），其中x＝1，y＝﹣1．
21．（6分）解方程：
（1）
（2）
22．（6分）如图所示，已知∠AOC＝2∠BOC，∠AOC的余角比∠BOC小30°
（1）求∠AOB的度数；
（2）过点O作射线OD，使得∠AOC＝4∠AOD，请你求出∠COD的度数．
23．（6分）如图，长为32米，宽为20米的长方形地面上，修筑宽度均为x米的两条互相垂直的小路（图中阴影部分），余下的部分作为耕地，如果将两条小路铺上地砖，选用地砖的价格是每平米40元．
（1）求买地砖至少需要多少元？（用含x的式子表示）
（2）计算当x＝2时，地砖的费用．
24．（8分）在某校举办的足球比赛中规定胜一场得3分，平一场得1分，负一场得0分，某班足球队参加了12场比赛，共得22分，已知这个队只输了2场，那么此队胜几场平几场？
25．（8分）已知数轴上点A表示的数为6，B是数轴上在原点左侧的一点，且A，B两点间的距离为10．动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．
（1）数轴上点B表示的数是 ；当点P运动到AB的中点时，它所表示的数是 ．
（2）动点Q从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，求：
①当点P运动多少秒时，点P追上点Q？
②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？
参考答案与试题解析
一、选择题
1-5:DBDBB 6-10:CCCAB 11-12:CC
二、填空题
13．
14．x＝12
15．120°
16．8
17．55°和35°
18．﹣5
三、解答题
19．解：（1）原式＝24×（﹣）+24×﹣24×
＝﹣20+9﹣2
＝﹣13；
（2）原式＝﹣1﹣8÷4×（5﹣9）
＝﹣1﹣2×（﹣4）
＝﹣1+8
＝7．
20．解：原式＝6x2﹣3xy+24﹣4xy﹣4x2
＝2x2﹣7xy+24，
当x＝1，y＝﹣1时，原式＝2×12﹣7×1×（﹣1）+24＝2+7+24＝33．
21．解：（1）移项，得：x﹣x＝1+3，
合并同类项，得：﹣x＝4，
系数化为1，得：x＝﹣8；
（2）去分母，得：3（3y﹣1）﹣12＝2（5y﹣7），
去括号，得：9y﹣3﹣12＝10y﹣14，
移项，得：9y﹣10y＝﹣14+3+12，
合并同类项，得：﹣y＝1，
系数化为1，得：y＝﹣1．
22．解：（1）设∠BOC＝x，则∠AOC＝2x，
依题意列方程90°﹣2x＝x﹣30°，
解得：x＝40°，
即∠AOB＝40°．
（2）由（1）得，∠AOC＝80°，
①当射线OD在∠AOC内部时，∠AOD＝20°，
则∠COD＝∠AOC﹣∠AOD＝60°；
②当射线OD在∠AOC外部时，∠AOD＝20°
则∠COD＝∠AOC+∠AOD＝100°．
23．解：（1）小路的面积为：32x+20x﹣x2，即52x﹣x2（平方米），
买地砖的金额为：40（52x﹣x2）＝2080x﹣40x2（元），
答：买地砖至少需要（2080x﹣40x2）元；
（2）当x＝2时，
2080x﹣40x2＝2080×2﹣40×22
＝4160﹣160
＝4000（元），
答：当x＝2时，地砖的费用为4000元．
24．解：设这支足球队胜x场，平y场，
依题意，得解得．
答：这支足球队胜了6场，平了4场．
25．解：（1）∵数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10，
∴得B点表示的数为﹣4，
当点P运动到AB的中点时，它所表示的数为（6﹣4）÷2＝1．
故答案为：﹣4、1；
（2）①根据题意得：6t﹣2t＝10，
解得t＝2.5．
答：当P运动2.5秒时，点P追上点Q；
②根据题意得：
当点P与点Q相遇前，距离8个单位长度：
2t+（10﹣6t）＝8，
解得t＝0.5；
当点P与点Q相遇后，距离8个单位长度：
（6t﹣10）﹣2t＝8，
解得t＝4.5．
答：当点P运动0.5秒或4.5秒时，点P与点Q间的距离为8个单位长度．