

2023-2024学年福建省福州四中桔园洲中学九年级(上)月考数学试卷(10月份)(含解析)
展开1.《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史让更多的观众走进博物馆,让一个个馆藏文物鲜活起来,所示四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )
A. B. C. D.
2.抛物线y=−2(x−2)2−5的顶点坐标是( )
A. (−2,5)B. (2,5)C. (−2,−5)D. (2,−5)
3.将二次函数y=5x2的图象先向右平移3个单位,再向下平移2个单位,得到的函数图象的解析式为( )
A. y=5(x+3)2+2B. y=5(x−3)2+2
C. y=5(x+3)2−2D. y=5(x−3)2−2
4.二次函数y=2x2+3的图象经过( )
A. 第一、二象限B. 第三、四象限C. 第一、三象限D. 第二、四象限
5.如图,将△ABC绕点C逆时针旋转一定的角度得到△A′B′C′,此点A在边B′C上,若BC=5,AC=3,则AB′的长为( )
A. 5B. 4C. 3D. 2
6.广东春季是流感的高发时期,某校4月初有一人患了流感,经过两轮传染后,共25人患流感,假设每轮传染中平均每人传染x人,则可列方程( )
A. 1+x+x2=25B. x+x2=25
C. (1+x)2=25D. x+x(1+x)=25
7.已知函数y1=mx2+n,y2=nx+m(mn≠0),则两个函数在同一坐标系中的图象可能为( )
A. B.
C. D.
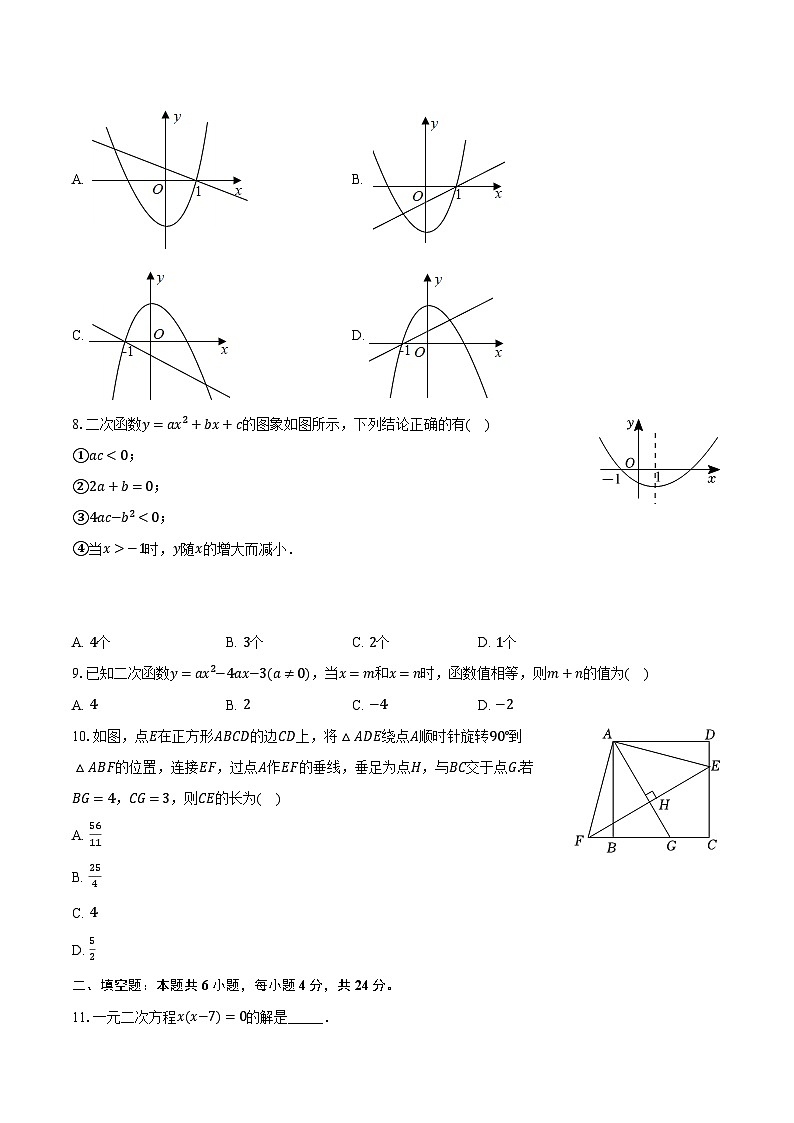
8.二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )
①ac<0;
②2a+b=0;
③4ac−b2<0;
④当x>−1时,y随x的增大而减小.
A. 4个B. 3个C. 2个D. 1个
9.已知二次函数y=ax2−4ax−3(a≠0),当x=m和x=n时,函数值相等,则m+n的值为( )
A. 4B. 2C. −4D. −2
10.如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若BG=4,CG=3,则CE的长为( )
A. 5611
B. 254
C. 4
D. 52
二、填空题:本题共6小题,每小题4分,共24分。
11.一元二次方程x(x−7)=0的解是_____.
12.在平面直角坐标系中,点P(−3,1)关于坐标原点中心对称的点P′的坐标是______.
13.二次函数y=x2+2x−2的最小值是______.
14.如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD的度数是 .
15.如图,二次函数y1=x2+bx+c与一次函数为y2=mx+n的图象相交于A,B两点,则不等式x2+bx+c
三、解答题:本题共9小题,共86分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
解下列方程:x2−3x=10.
18.(本小题8分)
求证:关于x的方程mx2−2x−14m+1=0,无论m取何值总有实数根.
19.(本小题8分)
如图,△ABC在平面直角坐标系xOy中的位置如图所示,A(−2,3),B(−1,1),C(0,2).
(1)将△ABC绕原点O顺时针旋转90°,作出旋转后的△A1B1C1;
(2)作出△A1B1C1关于点A1成中心对称的图形△A2B2C2,并写出对应点的坐标.
20.(本小题8分)
已知某二次函数的图象经过点(2,−6),当x=1时,函数的最大值为−4,求此二次函数的解析式,并说明点(−1,−12)是否在二次函数的图象上.
21.(本小题8分)
如图,△ABC中,∠C=90°,CA=CB=1,将△ABC绕点B顺时针旋转45°,得到△DBE(A、D两点为对应点),画出旋转后的图形,并求出线段AE的长.
22.(本小题10分)
已知二次函数y=−x2+2x.
(1)用配方法化为y=a(x−h)2+k的形式;
(2)该二次函数图象的顶点坐标为______;
(3)如图,用五点画图法在给出的坐标系中画出该二次函数的图象;
(4)根据图象,直接写出当−1
某创新公司生产营销A,B两种新产品,根据市场调研,发现如下信息:
信息1:平均每月销售A种产品4吨,每吨盈利4万元,经市场调查发现,如果每吨A产品降价0.1万元,公司平均每月可多销售0.2吨;设每月销售A种产品所获利润y(万元),所售产品数量x(吨).
信息2:销售B种产品所获利润y(万元)与所售产品数量x(吨)之间存在正比例函数关系y=2x.
根据以上信息,解答下列问题:
(1)求销售A种产品的最大利润;
(2)该公司准备生产营销A,B两种产品共10吨,且A种产品的数量不少于B种产品数量的23;求生产营销A,B两种产品各多少吨时,销售A,B两种产品所获得的利润之和最大.
24.(本小题12分)
如图,在三角形ABC中,AB=AC,∠BAC<60°,AD是BC边的高线,将线段AC绕点A逆时针旋转90°得到线段AE,连接BE交AD于点F.
(1)依题意补全图形,写出∠CAE= ______;
(2)求∠BAF+∠ABF和∠FBC的度数;
(3)用等式表示线段AF,BF,EF之间的数量关系,并证明.
25.(本小题14分)
已知抛物线y=ax2+bx−2经过(2,2),且顶点在y轴上.
(1)求抛物线解析式;
(2)直线y=kx+c与抛物线交于A,B两点.
①点P在抛物线上,当k=0,且△ABP为等边三角形时,求c的值;
②设直线y=kx+c交x轴于点M(m,0),线段AB的垂直平分线交y轴于点N,当c=1,m≥6,求点N纵坐标n的取值范围.
答案和解析
1.【答案】A
【解析】解:选项A能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形,选项B、C、D均不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形,
故选:A.
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,根据中心对称图形的概念求解.
本题主要考查了中心对称图形,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2.【答案】D
【解析】解:因为抛物线y=−2(x−2)2−5,
所以抛物线y=−2(x−2)2−5的顶点坐标是(2,−5).
故选:D.
根据二次函数性质,由顶点式直接写出顶点坐标即可.
本题考查了二次函数性质,由顶点式直接写出顶点坐标是解题关键.
3.【答案】D
【解析】解:由“左加右减”的原则可知,将二次函数y=5x2的图象先向右平移3个单位所得函数的解析式为:y=5(x−3)2;
由“上加下减”的原则可知,将二次函数y=5(x−2)2的图象先向下平移2个单位所得函数的解析式为:y=5(x−3)2−2.
故选:D.
直接根据“上加下减,左加右减”的原则进行解答即可.
本题考查的是二次函数的图象与几何变换,熟知函数图象几何变换的法则是解答此题的关键.
4.【答案】A
【解析】解:∵二次函数y=2x2+3中a=2>0,
∴开口向上,
∵函数的图象的顶点坐标为(0,3),
∴二次函数y=2x2+3的图象经过第一、二象限,
故选:A.
根据抛物线的开口方向和图象与y轴的交点坐标判断图象所处的位置即可.
本题考查了二次函数的性质,解题的关键是能够确定开口方向及顶点坐标,难度不大.
5.【答案】D
【解析】解:∵△ABC绕点C逆时针旋转一定的角度得到△A′B′C′,点A在边B′C上,
∴CB′=CB=5,
∴AB′=CB′−CA=5−3=2.
故选:D.
先根据旋转的性质得到CB′=CB=5,然后计算CB′−CA即可.
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
6.【答案】C
【解析】解:设每轮传染中平均一个人传染了x个人,依题意得1+x+x(1+x)=25,
即(1+x)2=25,
故选:C.
患流感的人把病毒传染给别人,自己仍然患病,包括在总数中.设每轮传染中平均一个人传染了x个人,则第一轮传染了x个人,第二轮作为传染源的是(x+1)人,则传染x(x+1)人,依题意列方程:1+x+x(1+x)=25即可.
本题考查了一元二次方程的应用,本题要注意的是,患流感的人把病毒传染给别人,自己仍然是患者,人数应该累加,这个问题和细胞分裂是不同的.
7.【答案】A
【解析】解:A、由一次函数y2=nx+m(mn≠0)的图象可得:n<0,m>0.此时二次函数y1=mx2+n的图象应该开口向上,抛物线与y轴交于负半轴,故选项不符合题意;
B、由一次函数y2=nx+m(mn≠0)的图象可得:n>0,m<0.此时二次函数y1=mx2+n的图象应该开口向下,抛物线与y轴交于正半轴,故本选项不符合题意;
C、由一次函数y2=nx+m(mn≠0)的图象可得:n<0,m<0.此时二次函数y1=mx2+n的图象应该开口向下,抛物线与y轴交于负半轴,故本选项不符合题意;
D、由一次函数y2=nx+m(mn≠0)的图象可得:n>0,m>0.此时二次函数y1=mx2+n的图象开口向上,抛物线与y轴交于正半轴,故本选项不符合题意;
故选:A.
可先根据一次函数的图象判断m的符号,再判断二次函数图象与实际是否相符,进而判断选项的正误.
考查一次函数及二次函数的图象与性质.熟练运用函数图象与系数的关系是解题的关键.
8.【答案】B
【解析】解:①∵抛物线开口向上,且与y轴交于负半轴,
∴a>0,c<0,
∴ac<0,
故结论①正确;
∵抛物线与x轴交于(−1,0),(3,0),
∴对称轴为直线x=−b2a=−1+32=1,
∴2a+b=0,故②正确;
③∵抛物线与x轴有两个交点,
∴b2−4ac>0,
即4ac−b2<0,
故结论③正确;
④∵抛物线开口向上,且抛物线对称轴为直线x=1,
所以当−1
故结论④错误;
故正确的结论有①②③共3个;
故选:B.
根据二次函数图象与系数的关系以及二次函数的性质,逐一分析判断即可.
本题主要考查抛物线与x轴的交点坐标,二次函数图象与函数系数之间的关系,解题的关键是掌握数形结合思想的应用,注意掌握二次函数图象与系数的关系.
9.【答案】A
【解析】解:∵当x=m和x=n时,y的值相等,
∴am2−4am−3=an2−4an−3,
解得:a(m−n)(m+n−4)=0.
∵a≠0,m≠n,
∴m+n−4=0,
即m+n=4,
故选:A.
根据题意可得出m+n=4,即可得出答案.
本题考查了二次函数图象上点的特征,解题关键是得出m与n的关系式.
10.【答案】A
【解析】解:如图所示,连接EG,
由旋转可得,△ADE≌△ABF,
∴AE=AF,DE=BF,
又∵AG⊥EF,
∴H为EF的中点,
∴AG垂直平分EF,
∴EG=FG,
设CE=x,则DE=7−x=BF,FG=CF−CG=11−x,
∴EG=11−x,
∵∠C=90°,
∴Rt△CEG中,CE2+CG2=EG2,即x2+32=(11−x)2,
解得x=5611,
∴CE的长为5611,
故选:A.
连接EG,根据AG垂直平分EF,即可得出EG=FG,设CE=x,则DE=7−x=BF,FG=EG=11−x,再根据Rt△CEG中,CE2+CG2=EG2,即可得到CE的长.
本题主要考查了正方形的性质,勾股定理以及旋转的性质,解题时注意:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
11.【答案】x1=0,x2=7
【解析】解:x=0或x−7=0,
所以x1=0,x2=7.
故答案为x1=0,x2=7.
利用因式分解的方法解方程.
本题考查了解一元二次方程−因式分解法:就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).
12.【答案】(3,−1)
【解析】解:根据关于原点对称的点的坐标的特征,得点P(−3,1)关于坐标原点中心对称的点P′的坐标是(3,−1).
故答案为:(3,−1).
根据关于原点对称的点的坐标的特征解决此题.
本题主要考查关于原点对称的点的坐标的特征,熟练掌握关于原点对称的点的坐标的特征是解决本题的关键.
13.【答案】−3
【解析】解:配方得:y=x2+2x−2=y=x2+2x+12−3=(x+1)2−3,
当x=−1时,二次函数y=x2+2x+2取得最小值为−3.
故答案为:−3.
把二次函数解析式整理成顶点式形式,然后写出最小值即可.
本题考查了二次函数的最值.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.
14.【答案】60°
【解析】解:如图,由题意及旋转变换的性质得:∠BOD=45°,
∵∠AOB=15°,
∴∠AOD=45°+15°=60°,
故答案为:60°.
如图,首先运用旋转变换的性质求出∠BOD的度数,结合∠AOB=15°,即可解决问题.
该题主要考查了旋转变换的性质及其应用问题;牢固掌握旋转变换的性质是灵活运用、解题的关键.
15.【答案】−1
∵当−1
16.【答案】12≤a<2
【解析】解:设直线MN的解析式为y=kx+b(k≠0),
则−k+b=−23k+b=2,
∴k=1b=−1,
∴MN的解析式为y=x−1,
∵A(x1,y1),B(x2,y2)是抛物线y=ax2−3x+1上的两点,其对称轴是直线x=x0,若|x1−x0|>|x2−x0|时,总有y1>y2,
∴a>0,
∵抛物线y=ax2−3x+1与线段MN有两个不相同的交点,
∴x=3时,y≥2,且抛物线与直线MN有交点,且−−32a≤3满足条件,
∴a≥12,
令x−1=ax2−3x+1,整理得:ax2−4x+2=0,
∵Δ=16−8a>0,
∴a<2,
∴12≤a<2,
故答案为:12≤a<2.
用待定系数法求出MN的解析式,根据二次函数的性质得出x=3时,y≥2,且−−32a≤3,进一步利用Δ>0求解即可.
本题考查二次函数的图象与系数的关系,二次函数的图象上的点的特征等知识,解题的关键是掌握二次函数的性质.
17.【答案】解:x2−3x=10.
x2−3x−10=0.
(x−5)(x+2)=0
(x−5)=0,(x+2)=0,
x1=5,x2=−2.
【解析】利用一拿会分解计算即可.
本题考查解一元二次方程−因式分解,正确进行因式分解是解题关键.
18.【答案】证明:当m=0时,−2x+1=0,
∴x=12,满足方程有实数根,
当m≠0时,
Δ=b2−4ac
=4−4×m×(−14m+1)
=m2−4m+4
=(m−2)2,
∵(m−2)2≥0,
∴Δ≥0,
∴方程总有实数根,
综上所述,无论m取何值总有实数根.
【解析】分m=0和m≠0,将数据代入Δ=b2−4ac,Δ≥0判断即可.
本题考查根的判别式,正确记忆公式是解题关键.
19.【答案】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求,A2(3,2),B2(5,3),C2(4,4)
【解析】(1)利用旋转变换的性质分别作出A,B,C的对应点A1,B1,C1即可;
(2)利用中心对称变换的性质分别作出B1,C1的对应点B2,C2即可.
本题考查作图−旋转变换,解题的关键是掌握旋转变换的性质,属于中考常考题型.
20.【答案】解:∵当x=1时,函数的最大值为−4,
∴二次函数顶点为(1,−4),
∴设二次函数y=a(x−h)2+k,
∵顶点为(1,−4),
∴y=a(x−1)2−4,
∵过点(2,−6),
∴−6=a−4,
∴a=−2,
∴y=−2(x−1)2−4,
当x=−1时,y=−2(−1−1)2−4=−12,
∴点(−1,−12)在二次函数的图象上.
【解析】根据题意得到抛物线的顶点坐标为(1,−4),于是可设顶点式y=a(x−1)2−4,然后把(2,−6)代入求出a的值即可.
本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.
21.【答案】解:如图,
∵∠C=90°,CA=CB=1,
∴∠ABC=45°,AB= 2BC= 2,
∵△ABC绕点B顺时针旋转45°,得到△DBE,
∴∠CBE=45°,BC=BE=1,
∵∠CBE=∠CBA,
∴点E在AB上,
∴AE=AB−BE= 2−1.
【解析】在BA上截取BE=BC,过点B作DB⊥BC,且DB=AB,则连接DE得到△DBE,再利用等腰三角形的性质得到∠ABC=45°,AB= 2BC= 2,利用旋转的性质得到∠CBE=45°,BC=BE=1,于是可判断点E在AB上,所以AE=AB−BE= 2−1.
本题考查了作图−旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了等腰直角三角形的性质.
22.【答案】(1,1) −3 0 1 0 −3
【解析】解:(1)y=−x2+2x=−(x−1)2+1;
(2)由(1)得:该函数图象的顶点坐标为(1,1);
故答案为:(1,1)
(3)解:列表如下:
画出该二次函数的图象如下:
(4)根据图象,当−1
(2)根据(1)中的顶点式,即可求解;
(3)利用描点法画出函数图象,即可求解;
(4)直接观察图象,即可求解.
本题主要考查了二次函数的图象和性质,画二次函数的图象,熟练掌握二次函数的图象和性质是解题的关键.
23.【答案】解:(1)依题意得:
y=[4−12(x−4)]x=−12x2+6x,
∵a=−12<0,
∴开口向下,有最大值,
x=−b2a=6,
当x=6时,ymax=18(万元),
所以销售A种产品的最大利润为18万元;
(2)设生产营销A中产品m吨,则B种产品为(10−m)吨,
∵A种产品的数量不少于B种产品数量的23,
∴m≥23(10−m),
∴m≥4,
∴4≤m≤10,
设利润为W,
则依题意得:
W=−12m2+6m+2(10−m)=−12m2+4m+20,
∵a=−12<0,
∴开口向下,有最大值,
所以m=−b2a=4,
∵4≤m≤10,
∴当m=4时,Wmax=28万元,
答:所以当生产营销A种产品4吨,B种产品6吨时,所获得的利润最大为28吨.
【解析】(1)根据题意及总利润=每吨A产品的利润x产品的销售数量,即可列出方程求解;
(2)根据A种产品的数量不少于B种产品数量的23,求出m的范围,设利润为W,根据题意即可列出关系式,配方后根据二次函数最值求法即可解答.
该题主要考查了二次函数的利润类应用题,解题的关键是根据题意找出等量关系式,列出对应的等式.
24.【答案】90°
【解析】解:(1)依题意补全图形,∠CAE=90°,
故答案为:90°;
(2)∵AC绕点A逆时针旋转90°得到线段AE,
∴∠CAE=90°,AC=AE,
∴∠ABE=∠E,
∵AB=AC,AD是BC边上的高,
∴∠BAD=∠CAD,
设∠BAD=∠CAD=α,
∴∠BAE=90°+2α,
∴∠ABE=∠E=[180°−(90°+2α)]÷2=45°−α,
∴∠BFD=∠ABF+∠BAF=45°−α+α=45°,
∵AD⊥BC,∠BFD=45°,
∴∠FBD=45°,
∴∠BAF+∠ABF的度数为45°,∠FBC的度数为45°;
(3)EF= 2AF+BF,理由如下:
过点A作AG⊥AF,交BE于点G,连接FC,如图2,
∴∠FAG=∠CAE=90°,
∴∠FAC+∠CAG=∠EAG+∠CAG,
∴∠FAC=∠EAG,
∵∠AFG=∠BFD=45°,
∴∠AGF=∠AFG=45°,
∴AF=AG,FG= 2AF,
在△ACF和△AEG中,
AC=AE∠FAC=∠GAEAF=AG,
∵AC=AE,
∴△ACF≌△AEG(SAS),
∴EG=CF,
∴EF=FG+EG= 2AF+CF,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴DF垂直平分BC,
∴BF=FC,
∴EF= 2AF+BF.
(1)根据旋转的性质画出图形即可;
(2)根据旋转的性质和三角形内角和定理解答即可;
(3)首先利用SAS证得△ACF≌△AEG),根据全等三角形的性质解答即可.
此题属于几何变换综合题,主要考查了旋转的性质,三角形内角和定理,全等三角形的判定和性质,解答本题的关键是熟练掌握旋转的性质和全等三角形的判定和性质.
25.【答案】解:(1)∵抛物线y=ax2+bx−2的顶点y轴上,
∴b=0,
∵抛物线y=ax2−2经过点(2,2),
∴2=4a−2,
∴a=1,
∴抛物线解析式为y=x2−2.
(2)①依题意得:当k=0时,AB⊥y轴,PA=PB=AB,
∴点P在AB的对称轴(y轴)上,
∴点P为抛物线的顶点,
即P(0,−2).
不妨设点A在点B的左侧,直线y=C与y轴交于点C.
∵∠APB=90°,CA=CB,
∴PB=2BC.PB2=BC2+PC2,
即(2BC)2=BC2+22,
∴BC=23 3,
∴点B(23 3,c),
把B(23 3,c)代入y=x2−2中,
得:c=(23 3)2−2=−23,
∴c的值为−23;
②如图2,直线y=kx+c,当c=1时,则y=kx+1,
∵直线y=kx+1与x轴交于点M(m,0),
∴mk+1=0,
∴k=−1m,
∵m≥6,
∴−16≤−1m<0,
∴−16≤k<0,
设A(x1,x12−2),B(x2,x22−2),
由y=kx+1y=x2−2,得x2−2=kx+1,
整理得x2−kx−3=0,
∵Δ=k2+12>0,
∴方程有两个不相等的实数根,
∴x1+x2=k,x1x2=−3,
∴x12+x22=(x1+x2)2−2x1x2=k2+6,
∵N(0,n),
∴AN2=x12+(x12−2−n)2,BN2=x22+(x22−2−n)2,
∵点N在AB的垂直平分线上,
∴AN=BN,
∴AN2=BN2,
∴x12+(x12−2−n)2=x22+(x22−2−n)2,
整理得(x12−x22)(x12+x22−2n−3)=0,
∵k≠0,
∴直线y=kx+1与x轴不平行,
∴A,B两点不关于y轴对称,
∴x1≠x2,
∴x12−x22≠0,
∴x12+x22−2n−3=0,
∴k2+6−2n−3=0,
∴n=12k2+32,
∴当k<0时,n随k的增大而减小,
若k=−16,则n=10972,
若k=0,则n=32,
∴点N纵坐标n的取值范围是32≤n<10972.
【解析】(1)先由抛物线y=ax2+bx−2的顶点在y轴上,确定b=0,再将(2,2)代入抛物线y=ax2−2,列方程求出a的值,即得到该抛物线的解析式为y=x2−2;
(2)①①根据题意作出图形,根据等腰直角三角形的性质可得PC=12AB=BC,根据B(c+2,c)在抛物线上,代入求解即可,根据图形取舍即可;
②当c=1时,则y=kx+1,由该直线经过点M(m,0),得mk+1=0,由m>6,可求得k的取值范围是−16<≤k<0,设A(x1,x12−2),B(x2,x22−2),由直线和抛物线的解析式联立方程组可求得x2−kx−3=0,则x1+x2=k,x1x2=−3,所以x12+x22=(x1+x2)2−2x1x2=k2+6,由AN2=BN2,得x12+(x12−2−n)2=x22+(x22−2−n)2,整理得(x12−x22)(x12+x22−2n−3)=0,则x12+x22−2n−3=0,所以k2+6−2n−3=0,得n=12k2+32,即可求得在−16≤k<0的范围内,n的取值范围是32≤n<10972.
此题重点考查二次函数的图象与性质、一次函数的图象与性质、用待定系数法求函数解析式、勾股定理的应用、一元二次方程根与系数的关系、等腰直角三角形的判定、线段的垂直平分线的性质等知识,此题综合性强,难度较大,属于考试压轴题.x
−1
0
1
2
3
y
______
______
______
______
______
x
−1
0
1
2
3
y
−3
0
1
0
−3
福建省福州第四中学桔园洲中学2023-2024学年上学期九年级12月月考数学试卷: 这是一份福建省福州第四中学桔园洲中学2023-2024学年上学期九年级12月月考数学试卷,共4页。
福建省福州第四中学桔园洲中学2023-2024学年上学期七年级12月月考数学试卷: 这是一份福建省福州第四中学桔园洲中学2023-2024学年上学期七年级12月月考数学试卷,共4页。
福建省福州第四中学桔园洲中学2023—2024学年上学期八年级10月月考数学试卷: 这是一份福建省福州第四中学桔园洲中学2023—2024学年上学期八年级10月月考数学试卷,共4页。












