

苏教版小学数学六年级下册期末复习专项训练题01——应用题(含答案+详细解析)
展开1.希望小学六(1)班同学每人都只参加了一项社团活动,参加社团活动的情况如图所示,参加足球社团活动的学生数比合唱社团多6人,参加书法社团的有多少人?
2.某市科学考试结果以等级形式呈现,分A、B、C、D四个等级。某校六年级为了迎接科学调测,进行了一次模拟考试,随机抽取部分学生的科学成绩进行调查统计,绘制成如下图所示两幅不完整的统计图。
(1)这次调测共抽取了( )名学生的科学成绩,将条形统计图补充完整。
(2)扇形统计图中,A等级所对应的扇形中,以圆心为顶点的角的度数为( )度。
(3)如果该学校六年级共有600名学生,估计一下这次模拟考试有( )名同学的科学成绩等级为A。
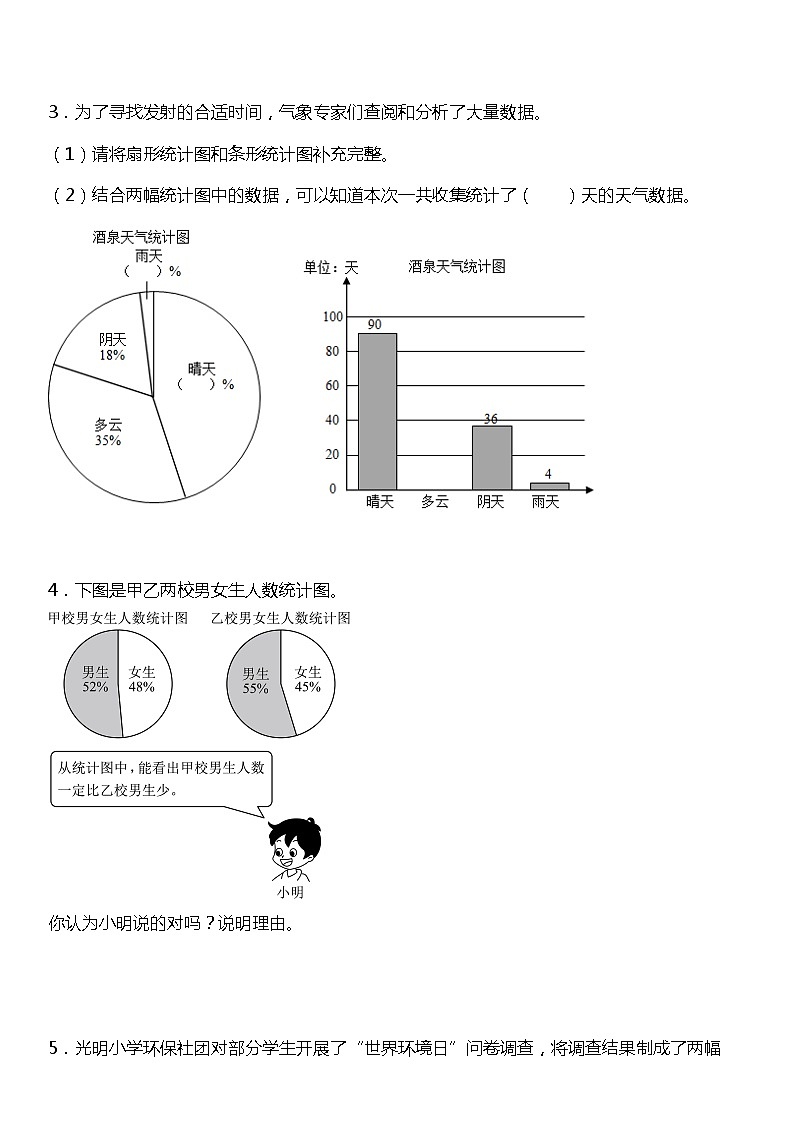
3.为了寻找发射的合适时间,气象专家们查阅和分析了大量数据。
(1)请将扇形统计图和条形统计图补充完整。
(2)结合两幅统计图中的数据,可以知道本次一共收集统计了( )天的天气数据。
4.下图是甲乙两校男女生人数统计图。
你认为小明说的对吗?说明理由。
5.光明小学环保社团对部分学生开展了“世界环境日”问卷调查,将调查结果制成了两幅统计图。
(1)条形统计图纵轴上每格表示( )人。
(2)选A项的学生有( )人,参与问卷的学生有( )人。
(3)选B项的学生人数比选A项的学生人数少( )%。
(4)选C项的学生有( )人,补齐上面的条形统计图。
(5)光明小学共有学生1700人,如果都参与问卷,根据上面的统计结果推测,选D项(随手乱扔垃圾)的会有多少人?你想对他们说什么?
6.如图是一个圆柱形粮囤的设计图纸:
(1)如果每立方米稻谷约重500千克,那么这个粮囤大约能装多少吨稻谷?
(2)给这个粮囤外围(不含顶部)喷涂防锈油漆,按照每千克油漆可以喷涂1.5平方米计算,至少需要多少千克油漆?
7.妈妈的茶杯,这样放在桌上。(如图)茶杯中部的一圈装饰带好看吧,那是小明怕烫伤妈妈的手特意贴上的,这条装饰带宽5厘米,接头处15毫米,这条装饰带有多少平方厘米?
8.一个圆柱形油桶,底面内直径为4分米,高5分米,如果每升柴油重0.85千克,这个油
桶可装柴油多少千克?
9.长征二号运载火箭顶部是逃逸塔发动机部分,为研究方便制作了一个模型(如图),它的下底面直径是6分米,上底面直径是3分米,高8分米,这个模型的体积是多少立方分米?
10.君君用橡皮泥捏了一个高3厘米的圆柱体,后来又将这个圆柱的高增加了2厘米(如图),现在圆柱的表面积比原来增加了12.56平方厘米,原来圆柱的体积是多少立方厘米?
11.古代的铜钱都是“外圆内方”,铜钱内正方形的边长是0.5厘米。小明把20枚相同的古代铜钱叠在一起的形状如图,每枚铜钱的体积是多少立方厘米?(取值3.14)
12.2022年4月16日,神舟十三号宇宙飞船搭载我国三名航天员成功返回地球。飞船制造时需要将一块底面半径2厘米,长0.5米的圆柱体钛合金材料,压铸成宽20厘米,厚5毫米的长方体钛合金板材,该板材长多少厘米?
13.有一个底面内直径是20厘米的圆柱形水杯,里面浸没着一个底面半径是6厘米、高是12厘米的圆锥形铅锤,当取出铅锤后,杯里的水下降了多少厘米?
14.现在把一堆小麦堆成圆锥形,已知它的底的周长是12.56m,高是1.2m。已知每立方米小麦重750千克,求这堆小麦共重多少千克?
15.下图是一个圆柱。按要求画一画,算一算。
(1)在方格纸上画出这个圆柱的展开图。(侧面沿高剪开)
(2)请列式计算出这个圆柱的表面积。
16.驼鹿是某岛上狼的重要食物来源,从1965年至1975年,驼鹿的数量增加了,达到1200只,由于食物充足,狼的数量达到50只,不断增加的狼捕食了越来越多的驼鹿,到1980年,驼鹿的数量又减少到400只,同时狼的数量也急剧减少,与1975年数量比是2∶5。
(1)1965年至1975年之前,驼鹿的数量多少只?
(2)1980年狼的数量是多少只?
17.某市居民原来每户每月用水缴费标准为2.00元/立方米,考虑物价、环境保护等因素,自今年5月1日起,每户每月用水缴费标准作如下调整:
按新的收费标准,李叔叔家今年5月份的水费比原来多缴纳16.80元。他家今年5月份的用水量是多少?
18.甲、乙两人同时从A地骑车到B地,经过10分钟,乙到达B地,甲距B地还有1200米。已知甲、乙两人骑车的平均速度比为2∶3,A、B两地相距多远?
19.一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只,如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
20.中国空间站建设凝聚了许多科研工作者的心血与汗水,火箭研发中心、飞船研发中心、材料研发中心都有许多科研工作者。其中火箭研发中心有160人,关于这三个研发中心的科研工作者人数还有以下的信息,请选择合适的信息解答问题。
①火箭研发中心的人数是总人数的;
②飞船研发中心、火箭研发中心两个中心的人数比是3∶4;
③材料研发中心人数比飞船研发中心人数多;
④材料研发中心人数比总人数的40%多8人。
请选择合适信息,计算材料研发中心有科技工作者多少人?
21.在比例尺是1∶5000000的地图上量得甲、乙两地相距7厘米,一辆客车和一辆货车分别从甲、乙两地同时出发相向而行,2小时相遇。已知客车与货车的速度比是4∶3,那么货车的速度是多少千米/时?
22.在比例尺是的地图上,量得武汉到郑州的距离是10厘米。刘师傅去执行“抗疫物资运输”任务,如果运输车以每小时80千米的速度于20时20分出发,什么时候能到达目的地?
23.新冠肺炎疫情期间,一列货车满载医疗物资驰援山西太谷,先用2小时行驶了120千米,照这样的速度,行完剩下的180千米路程还要多少小时?明明和林林有两种不同的解题思路,请你先选择一种你喜欢的解答,再试试另一种方法。
明明:按照“先行的速度=剩下行驶的速度”这样关系列式用比例方法解答。
林林:先求出剩下的行驶时间是已行的几分之几;再用分数乘法解答。
24.某地区出产的花生出量非常高,100千克花生可以榨油20千克。照这样计算,榨10吨花生油,要用花生多少吨?(用比例解)
25.高速铁路通车后,大大节约了人们的出行时间。在一幅比例尺为1∶3500000的地图上,小军量得盐城站到上海虹桥站的图上距离约是9厘米。一列高速动车平均每小时行210千米,它从盐城站出发,行驶到上海虹桥站至少要多少小时?
26.小明用240毫升的酸梅原汁加水调制了600毫升酸梅汤,妈妈说,当酸梅汤原汁和水的比是3:7时,口感最佳。为了使调制的酸梅汤口感最佳,小明应再往酸梅汤中加水多少毫升?
27.如图,一根弹簧挂上物体(质量不超过40千克)后长度会成比例伸长,下图表示一个物体的质量和弹簧伸长的长度之间的关系。
(1)物体的质量与弹簧伸长的长度成( )比例。
(2)如果挂上8千克的物体,那么弹簧应伸长( )厘米。
(3)要使弹簧伸长8厘米,应挂上( )千克的物体。
28.甲、乙、丙三人进行100米短跑赛。甲到终点时,乙跑了80米,丙离终点30米。那么,当乙到终点时,丙离终点还有多远?(用比例解)
29.爸爸打算给亮亮的小书房铺上方砖,用边长2分米的方砖需要90块,如果改用边长3分米的方砖,需要方砖多少块?
30.有一个两层水箱,如图所示。(单位:分米)
(1)第一层水箱容积是( )升,第二层的容积是( )升。
(2)如果注满第一层需要7.2分钟,照这样的流速,注满整个水箱需要多少分钟?
(3)在注满整个水箱的过程中,注水的高度随着时间的延长而增加,下面哪幅图表示正确的注水情况,请在图上打“√”。
31.一条生产线每3分钟自动记录一次生产产品的总数量,下面是生产产品情况的记录。
(1)生产产品的时间和产品数量成( )比例。
(2)照这样计算,45分钟生产产品多少个?
32.用15克糖和210克水配制成一杯糖水,如果保持糖水一样甜,加入140克水后需加入多少克糖?
33.84消毒液在生活中广泛应用。下面是某品牌84消毒液说明书。
【药品名称】84消毒液
【规格型号】500mL
【用法用量】见下表
学校要配置消毒水对班级的课桌面进行消毒,用200mL的消毒液需要用多少L水来配?
34.爸爸开车去某地出差,已知路程是132千米,汽车油箱一共可以装油55升,汽油单价是9元/升,出发和到达时油箱里油量分别如下。
(1)这次行程汽油费花了多少钱?
(2)加满一箱油可以行驶多少千米?
参考答案:
1.8人
【分析】用参加足球社团活动的学生数占总人数的百分率减去参加合唱社团活动的学生数占总人数的百分率,求出参加足球社团活动的学生数占总人数的百分率比参加合唱社团活动的学生数占总人数的百分率多百分之几,再用6人除以多的百分率,即可求出总人数,最后用总人数乘参加书法社团的学生数占总人数的百分率,即可求出参加书法社团的有多少人。
【详解】6÷(40%-25%)×20%
=6÷15%×20%
=40×20%
=8(人)
答:参加书法社团的有8人。
【点睛】此题考查扇形统计图的分析、百分数的计算及应用,理解题意,找出数量关系,列式计算即可。
2.(1)50,图见详解
(2)108
(3)180
【分析】(1)把调测的总人数看成单位“1”,D等级有5人,占10%,根据已知一个数的百分之几是多少,求这个数,用除法解答。用总人数减去已知人数求出A等级的人数,完成统计图。
(2)根据求一个数是另一个数的百分之几,用除法求出等级A占总人数的百分之几,周角是360度,根据求一个数的百分之几是多少,用乘法解答。
(3)根据一个数乘百分数的意义,用乘法解答。
【详解】(1)5÷10%
=5÷0.1
=50(名)
50-(22+8+5)
=50-35
=15(名)
统计图如下:
(2)15÷50×100%
=0.3×100%
=30%
360×30%=360×0.3=108(度)
(3)600×30%=600×0.3=180(名)
【点睛】此题考查的目的是理解掌握扇形统计图、条形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
3.(1)见详解;(2)200
【分析】(1)用阴天的天数除以它占的百分率,得出一共统计的天数,分别用晴天和雨天的天数除以一共统计的天数,即可求出它们占的百分率,再用减法计算出多云的天数,补充统计图即可;
(2)用阴天的天数除以它占的百分率,得出一共统计的天数。
【详解】(1)36÷18%=200(天)
90÷200×100%=45%
4÷200×100%=2%
200-90-36-4
=110-36-4
=70(天)
(2)36÷18%=200(天)
本次一共收集统计了200天的天气数据。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
4.不对,因为甲乙两校的总人数不知道。
【分析】甲、乙两个学校的学生人数不一定相同,所以男生人数的多的学校,是由学校总人数决定。
【详解】根据分析可知;小明说法不对,因为甲乙两校的总人数不知道,所以不能看出哪个学校的男生人数多。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
5.(1)30;
(2)150,300;
(3)80;
(4)90;条形统计图见详解;
(5)170人,我想对这部同学说将垃圾放到规定地点,并把垃圾分类放置,保护环境,从自身做起。(答案不唯一)
【分析】(1)通过观察条形统计图的纵轴可知,每格表示30人;
(2)把参与问卷的学生总人数看作单位“1”,选A项的学生有150人,占总人数的50%,根据已知一个数的百分之几是多少,求这个数,用除法解答;
(3)把选A项的学生人数看作单位“1”,先求出选B项的学生人数比选A项的学生人数少多少人,再根据求一个数是另一个数的百分之几,用除法解答;
(4)根据减法的意义,用减法求出选C项的人数,据此完成统计图;
(5)把全校学生人数看作单位“1”,根据求一个数的几分之几是多少,用乘法解答;我想对这部同学说将垃圾放到规定地点,并把垃圾分类放置,保护环境,从自身做起。(答案不唯一)
【详解】(1)条形统计图纵轴上每格表示30人。
(2)150÷50%=300(人)
选A项的学生有150人,参与问卷的学生有300人。
(3)
(150-30)÷150
=120÷150
=0.8
=80%
选B项的学生人数比选A项的学生人数少80%。
(4)
300-(150+30+30)
=300-210
=90(人)
选C项的学生有90人。
作图如下:
(5)30÷300×100%=10%
1700×10%=170(人)
选D项(随手乱扔垃圾)的会有170人,我想对这部同学说将垃圾放到规定地点,并把垃圾分类放置,保护环境,从自身做起。(答案不唯一)
【点睛】此题考查的目的是理解掌握扇形统计图、条形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
6.(1)70.65吨;
(2)81.64千克
【分析】(1)圆柱形粮囤的直径为6米,高为5米,根据圆柱的体积(容积)公式:V=,代入数据求出圆柱形粮囤的容积,再乘每立方米稻谷的重量,即可求出这个粮囤大约能装多少千克稻谷,再进行单位换算即可。
(2)粮囤外围(不含顶部)的面积相当于圆柱的侧面积和底面积之和,根据圆柱的表面积公式:S=,求出粮囤外围的面积,再除以每千克油漆喷涂的面积,即可求出需要多少千克油漆。
【详解】(1)3.14×(6÷2)2×5×500
=3.14×32×5×500
=3.14×9×5×500
=28.26×5×500
=70650(千克)
70650千克=70.65吨
答:这个粮囤大约能装70.65吨稻谷。
(2)3.14×(6÷2)2+3.14×6×5
=3.14×32+94.2
=3.14×9+94.2
=28.26+94.2
=122.46(平方米)
122.46÷1.5=81.64(千克)
答:至少需要81.64千克油漆。
【点睛】此题的解题关键是灵活运用圆柱的表面积和体积公式,解决实际的问题。
7.101.7平方厘米
【分析】根据圆柱的侧面积公式:S=,h=5厘米,d=6厘米,代入求出装饰带贴在杯子上的面积,再利用长方形的面积,用接头处的长度乘装饰带的高度,求出接头处的面积,再加上贴在杯子上的装饰带的面积,即是整条装饰带的面积。
【详解】15毫米=1.5厘米
3.14×6×5+1.5×5
=94.2+7.5
=101.7(平方厘米)
答:这条装饰带有101.7平方厘米。
【点睛】此题的解题关键是掌握圆柱的侧面积计算方法,注意此题还要计算接头处的面积。
8.53.38千克
【分析】先利用公式r=d÷2,求出圆柱的底面半径,再根据圆柱的体积公式:V=,代入数据求出圆柱形油桶的体积,由于1升=1立方分米,转换单位,之后再乘每升柴油的重量,即可求出这个油桶可装柴油的重量。
【详解】3.14×(4÷2)2×5
=3.14×22×5
=3.14×4×5
=62.8(立方分米)
62.8立方分米=62.8升
62.8×0.85=53.38(千克)
答:这个油桶可装柴油53.38千克。
【点睛】此题的解题关键是灵活运用圆柱的体积(容积)公式解决实际问题。
9.131.88立方分米
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式求出大小两个圆锥的体积差即可。
【详解】×3.14×(6÷2)2×(8×2)−×3.14×(3÷2)2×8
=×3.14×9×16-×3.14×2.25×8
=150.72-18.84
=131.88(立方分米)
答:这个模型的体积是131.88立方分米。
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
10.9.42立方厘米
【分析】要求圆柱的体积,已知圆柱的高,还要求圆柱的直径;根据题干圆柱的高增加了2厘米,表面积比原来增加了12.56平方厘米,由此利用圆柱的侧面积公式即可求得圆柱的直径,代入圆柱的体积公式即可解决问题。
【详解】12.56÷2÷3.14÷2
=6.28÷3.14÷2
=2÷2
=1(厘米)
3.14×12×3
=3.14×3
=9.42(立方厘米)
答:原来圆柱的体积是9.42立方厘米。
【点睛】本题实际是对圆柱侧面积及体积计算公式的考查,圆柱的侧面积=πdh,圆柱的体积=底面积×高。
11.0.578立方厘米
【分析】根据图示可知,20枚相同的古代铜钱叠在一起的体积等于圆柱的体积减去长方体的体积。利用圆柱的体积公式:V=πr2h,长方体体积公式:V=abh,计算出20枚铜钱的体积,再除以20即可求出每枚铜钱的体积。
【详解】3.14×(2÷2)2×4-0.5×0.5×4
=12.56-1
=11.56(立方厘米)
11.56÷20=0.578(立方厘米)
答:每枚铜钱的体积是0.578立方厘米。
【点睛】本题主要考查组合图形的体积,关键利用圆柱、长方体的体积公式计算。
12.62.8厘米
【分析】先根据圆柱的体积V=πr2h求出钛合金材料的体积,再除以长方体的宽和高就是长方体的长,注意单位的换算。
【详解】0.5米=50厘米
5毫米=0.5厘米
3.14×22×50÷20÷0.5
=628÷20÷0.5
=62.8(厘米)
答:该板材长62.8厘米。
【点睛】此题考查长方体、圆柱体的体积公式的灵活应用,解答此题的关键是明确熔铸前后的体积不变。
13.1.44厘米
【分析】根据圆锥的体积公式:V=πr2h,据此求出铅锤的体积。铅锤的体积等于下降的水的体积。圆柱的体积公式:V=Sh,那么h=V÷S,用圆锥的体积除以圆柱的底面积即可。
【详解】×3.14×62×12÷[3.14×(20÷2)2]
=×3.14×36×12÷[3.14×100]
=452.16÷314
=1.44(厘米)
答:杯里的水下降了1.44厘米。
【点睛】此题主要考查圆锥、圆柱体积公式的灵活运用。明确铅锤的体积等于下降的水的体积是解题的关键。
14.3768千克
【分析】圆锥底面周长已知,进而求出底面半径,再利用圆锥的体积公式求出小麦堆的体积,然后用小麦的体积乘每立方米小麦的重量即可。
【详解】圆锥的底面半径:12.56÷3.14÷2=2(米)
麦堆的体积:×3.14×22×1.2
=×3.14×4×1.2
=12.56×0.4
=5.024(立方米)
小麦的重量:750×5.024=3768(千克)
答:这堆小麦共重3768千克。
【点睛】此题主要考查圆锥体积公式的实际应用。
15.(1)见详解;
(2)25.12cm2
【分析】(1)圆柱侧面沿高剪开成一个长方形,长是圆柱的底面周长,宽是圆柱的高,底面展开是两个圆;据此解答;
(2)圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高,代入数据计算即可。
【详解】(1)底面周长:3.14×1×2
=3.14×2
=6.28(cm)
画图如下:
(2)3.14×1×1×2+6.28×3
=6.28+18.84
=25.12(cm2)
答:这个圆柱的表面积是25.12cm2。
【点睛】本题主要考查圆柱展开图及圆柱的表面积公式。
16.(1)750只;
(2)20只
【分析】(1)设1965年至1975年之前,驼鹿的数量x只,根据等量关系式:1965年至1975年之前,驼鹿的数量×(1+)=1200,据此列方程解答即可;
(2)由题意可知,1975年狼的数量达到50只,1980年狼的数量与1975年狼的数量的比是2∶5,据此列比例解答即可。
【详解】(1)解:设1965年至1975年之前,驼鹿的数量x只。
x=750
答:1965年至1975年之前,驼鹿的数量750只。
(2)解:设1980年狼的数量是x只。
2∶5=x∶50
5x=2×50
5x=100
x=20
答:1980年狼的数量是20只。
【点睛】本题考查用方程解决实际问题和比的应用,明确等量关系是解题的关键。
17.26立方米
【分析】根据题意,多缴的16.80元,可分为18立方米以下,和18立方米以上两部分多缴的,分别求出现在比原来每立方米多缴的钱数,就可以求出18立方米以上部分是多少立方米,再与18立方米合并起来即可。
【详解】18立方米以下,每立方米多缴:2.40-2.00=0.4(元)
18立方米一共多缴:18×0.40=7.2(元)
18立方米以上每立方米多缴:3.20-2.00=1.2(元)
18立方米以上的用水量是:
(16.8-7.2)÷1.2
=9.6÷1.2
=8(立方米)
这个月的用水量是:18+8=26(立方米)
答:他家今年5月份的用水量是26立方米。
【点睛】此题数量关系比较复杂,解答时首先弄清现在比原来多缴的钱,要分成两部分计算。
18.3600米
【分析】根据题意,甲、乙两人骑车的平均速度比为2∶3,经过10分钟,乙到达B地,甲距B地还有1200米,可以找出等量关系是:甲的速度×10分钟+1200=乙的速度×10分钟。据此解答即可。
【详解】解:根据甲、乙两人骑车的平均速度比为2∶3,设甲速度为2x米/分钟,乙的速度为3x米/分钟。
2x×10+1200=3x×10
20x+1200=30x
10x=1200
x=120
乙的速度为:3x=3×120=360(米/分钟)
A、B两地相距:360×10=3600(米)
答:A、B两地相距3600米。
【点睛】本题考查了行程问题,关键是得出等量关系:甲的速度×10分钟+1200=乙的速度×10分钟。
19.蜘蛛10只;蚱蜢15只
【分析】设蜘蛛x只,则蚱蜢有(25-x)只,根据蜘蛛数量×腿数+蚱蜢数量×腿数=总腿数,列出方程求出x的值是蜘蛛数量,总数量-蜘蛛数量=蚱蜢数量。
【详解】解:设蜘蛛x只。
8x+(25-x)×6=170
8x+150-6x=170
2x+150-150=170-150
2x÷2=20÷2
x=10
25-10=15(只)
答:蜘蛛有10只,蚱蜢有15只。
【点睛】用方程解决问题的关键是找到等量关系,本题也可以用假设法进行解答。
20.①④,200人。
【分析】选择①④,用火箭研发中心的人数除以火箭研发中心的人数占总人数的分率,得出总人数,再乘40%,最后加8人,即可得材料研发中心有科技工作者的人数。
【详解】①④
160÷×40%+8
=480×40%+8
=192+8
=200(人)
答:材料研发中心有科技工作者200人。
【点睛】本题主要考查了比的应用,已知一个数的几分之几是多少,求这个数,用除法计算;已知一个数,求它的百分之几是多少,用乘法计算。
21.75千米/时
【分析】根据“实际距离=图上距离÷比例尺”,即可求得甲、乙两地的实际距离,再除以相遇时间,求出两辆车的速度和,进而利用按比例分配的方法求出货车每小时行的千米数。
【详解】7÷=35000000(厘米)=350(千米)
350÷2=175(千米/时)
175×
=175×
=75(千米/时)
答:货车的速度是75千米/时。
【点睛】此题主要考查比例尺、图上距离和实际距离之间的关系,也考查了简单的行程问题和按比例分配的问题。
22.第二天早上2时35分到达
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出武汉到郑州的实际距离,再根据时间=距离÷速度,求出所用的时间,即可解答。
【详解】10÷
=10×5000000
=50000000(厘米)
50000000厘米=500千米
500÷80=6.25(小时)
6.25小时=6时15分
20时20分+6时15分=26时35分
26时35分-24时=2时35分
答:第二天早上2时35分到达。
【点睛】根据图上距离和实际距离的换算;距离,时间和速度三者之间的关系进行解答;关键是最后的时间确定清楚。
23.3小时
【分析】照这样速度,速度不变,那么路程和时间成正比,即比值一定,所以按照“先行的速度=剩下行驶的速度”这样关系列式,设行完剩下的180千米路程还要小时,用比例方法解答。
同理,因为速度一定,路程和时间成正比,先求出剩下的行驶时间是已行的几分之几,即求剩下的路程是已行路程的几分之几,再根据分数乘法的意义作答。
【详解】方法一:
解:设行完剩下的180千米,还要小时。
答:行完剩下的180千米路程还要3小时。
方法二:
(小时)
答:行完剩下的180千米路程还要3小时。
【点睛】本题考查了解答应用题方法的多样性,考虑问题的角度不同,解答方法就不同,要灵活应用。
24.50吨
【分析】由题意可得,某地区出产的花生的出油率是一定的,则榨的花生油的重量与花生的重量成正比例关系,据此即可列比例求解。
【详解】解:设榨10吨花生油,要用花生x吨。
20∶100=10∶x
20x=100×10
20x=1000
20x÷20=1000÷20
x=50
答:榨10吨花生油,要用花生50吨。
【点睛】本题考查了用比例解决问题,注意找出两种相关联的量是成正比例还是反比例。
25.1.5小时
【分析】根据公式:实际距离=图上距离÷比例尺,把数代入公式即可求出实际距离,再根据1千米=100000厘米,转换单位,再根据公式:时间=路程÷速度,把数代入公式即可求解。
【详解】9÷=31500000(厘米)
31500000厘米=315(千米)
315÷210=1.5(小时)
答:行驶到上海虹桥站至少需要1.5小时。
【点睛】本题主要考查图上距离和实际距离的公式,熟练掌握它的公式并灵活运用。
26.200毫升
【分析】根据酸梅汤原汁和水的比是3∶7,可设需要加水x毫升,列出比例240∶(600-240+x)=3∶7计算求解即可。
【详解】解:设需要加水x毫升,
240∶(600-240+x)=3∶7
(360+x)×3=240×7
1080+3x=1680
1080+3x-1080=1680-1080
3x=600
3x÷3=600÷3
x=200;
答:小明应再往酸梅汤中加水200毫升。
【点睛】当酸梅汤原汁和水的比是3∶7时,关键为“酸梅原汁的质量不变”,只是改变水的质量。
27.(1)正
(2)2
(3)32
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,由题,2∶0.5=4∶1=4(一定),即物体的质量∶弹簧伸长的长度=4(一定),所以物体的质量与弹簧伸长的长度成正比例;
(2)挂上8千克的物体,8千克<40千克,弹簧长度会成比例伸长,那么弹簧伸长的长度=物体的质量÷4,据此代入数据解答;
(3)由(1)可知,物体的质量=弹簧伸长的长度×4,据此代入数据解答。
(1)
2∶0.5=4∶1=4(比值一定)
所以物体的质量与弹簧伸长的长度成正比例。
(2)
8÷4=2(厘米)
所以挂上8千克的物体,弹簧应伸长2厘米。
(3)
8×4=32(千克)
所以要使弹簧伸长8厘米,应挂上32千克的物体。
【点睛】此题属于辨识成正、反比例的量以及正比例的应用题;两个量是对应的比值一定,这两个量成正比例关系;两个量的乘积一定,则这两个量成反比例关系。
28.12.5米
【分析】首先根据速度×时间=路程,可得时间一定时,速度和路程成正比例,据此求出乙和丙的速度的比;然后设当乙到终点时,丙还有x米,根据乙丙跑的路程的比=乙丙的速度比,列出比例,求出当乙到终点时,丙还有多少米即可。
【详解】80∶(100-30)
=80∶70
=8∶7
解:设当乙到终点时,丙还有x米,
100∶(100-x)=8∶7
8×(100-x)=100×7
800-8x=700
800-8x+8x=700+8x
700+8x=800
700+8x-700=800-700
8x=100
8x÷8=100÷8
x=12.5
答:丙离终点还有12.5米。
【点睛】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握;解答此题的关键是求出乙丙的速度的比是多少。
29.40块
【分析】解答此题时应先想书房的面积一定,也就是每块的面积和块数的乘积是一定的,即一块方砖的面积与方砖的块数成反比例,根据已知条件列方程解答即可。
【详解】解:设需要方砖x块。
3×3×x=2×2×90
9x=360
x=40
答:需要方砖40块。
【点睛】解决此题关键是判断出一块方砖的面积与方砖的块数成反比例,注意3分米和2分米都是方砖的边长,而不是方砖的面积。
30.(1)60;100;
(2)19.2分钟;
(3)见详解
【分析】(1)利用长方体体积=长×宽×高,代入数值,即可解答。
(2)根据水流速度不变,列比例式解答。
(3)根据注水的高度和时间成正比例关系,据此解答。
【详解】(1)6×5×2=60(立方分米)
60立方分米=60升
(6+2+2)×5×2
=10×5×2
=100(立方分米)
100立方分米=100升
(2)解:设注满整个水箱需要x分钟,得:
7.2∶60=x∶(100+60)
60x=7.2×160
60x÷60=1152÷60
x=19.2
注满整个水箱需要19.2分钟。
(3)
【点睛】本题考查了容积的求法、列比例解决问题、正比例关系图像的判断,需灵活掌握并会应用。
31.(1)正;
(2)765个。
【分析】两个相关联的量,若两个量的比值一定,两个量成正比例关系;若两个量的乘积一定,两个量成反比例关系,据此判断即可。
【详解】(1)51∶3=102∶6=153∶9=204∶12=17
生产产品的时间和产品数量成正比例。
(2)17×45=765(个)
答:45分钟生产产品765个。
【点睛】根据正比例的判断方法,解答此题即可。
32.10克
【分析】根据题意,设加入140克水后需要加入x克糖,加入x克糖,糖的质量是(x+15)克,水的质量是(210+140)克;糖与水的比不变,即糖与水的比成正比例;列比例:15∶210=(x+15)∶(210+140),解比例,即可解答。
【详解】解:设加入140克水后需要加入x克糖。
15∶210=(x+15)∶(210+140)
210×(x+15)=15×350
210x+210×15=5250
210x+3150=5250
210x=5250-3150
210x=2100
x=2100÷210
x=10
答:加入140克水后需要加入10克糖。
【点睛】解答本题的关键先判断糖与水成什么比例,再根据判断的比例,设出未知数,列比例,再解比例。
33.20L
【分析】根据统计表可知,学校要配置消毒液对班级课桌面进行消毒,需要稀释的比例是1∶100;即消毒液与水比成正比例;设用200mL的消毒液需要用水xmL水来配;列比例:1∶100=200∶x;解比例,即可解答。
【详解】解:设用200mL的消毒液需要用xmL水来配。
1∶100=200∶x
x=100×200
x=20000
20000mL=20L
答:用200mL的消毒液需要用20L水来配。
【点睛】解答本题的关系判断出消毒液与水成什么比;再根据判断的比例,设出未知数,找出相关的量,列比例,解比例,注意单位名数的换算。
34.(1)99元(2)660千米
【分析】(1)观察出发和到达时油箱里的油量可知,出发时的油量占油箱总量的,到达时油箱里的油量占油箱总量的,则这次行程用去了油箱总量的(-),用油箱总量乘(-)即可求出这次行程的用油量。最后用汽油的单价乘用油量即可求出这次行程汽油费花了多少钱。
(2)=每升汽油可以行驶的路程(一定),则行驶的路程和用油量成正比例。根据题意,设加满一箱油可以行驶x千米,可列出比例:x∶55=132∶11,解出比例即可。
【详解】(1)55×(-)
=55×
=11(升)
11×9=99(升)
答:这次行程汽油费花了99元。
(2)解:设加满一箱油可以行驶x千米。
x∶55=132∶11
11x=132×55
x=132×55÷11
x=660
答:加满一箱油可以行驶660千米。
【点睛】本题考查了分数四则混合运算和正比例的应用。观察示意图,得出这次行程的用油量占油箱总量的分率,继而求出用油量是解题的关键。
小问卷A.能将垃圾放到规定的地方,还会考虑垃圾的分类
B.能将垃圾放到规定的地方,但不会考虑垃圾的分类
C.偶尔会将垃圾放到规定的地方
D.随手乱扔垃圾
用水量
收费标准
18立方米及以下
2.40元/立方米
18立方米以上的部分
3.20元/立方米
时间/分
3
6
9
12
…
产品数量/个
51
102
153
204
…
消毒对象
稀释比例(消毒液:水)
消毒时间(分钟)
使用方法
一般物品表面
1∶100
20
浸泡或擦拭
餐饮具
1∶200
20
浸泡或擦拭
白色衣物清洗
1∶250
30
浸泡
……
苏教版小学数学六年级下册期末复习专项训练题练03——脱式计算(含答案+详细解析): 这是一份苏教版小学数学六年级下册期末复习专项训练题练03——脱式计算(含答案+详细解析),共37页。试卷主要包含了计算下面各题,能简算的要简算,计算下面各题,怎样简便就怎样算,用适当的方法递等式计算,脱式计算,能简算的要简算,脱式计算,下面各题怎样简便就怎样算等内容,欢迎下载使用。
苏教版小学数学六年级下册期末复习专项训练题09——判断题(含答案+详细解析): 这是一份苏教版小学数学六年级下册期末复习专项训练题09——判断题(含答案+详细解析),共23页。试卷主要包含了圆柱的每个面都是圆形,在一平面上,点表示的位置不存在,解比例的依据是比的基本性质等内容,欢迎下载使用。
苏教版小学数学六年级下册期末复习专项训练题08——填空题(含答案+详细解析): 这是一份苏教版小学数学六年级下册期末复习专项训练题08——填空题(含答案+详细解析),共38页。试卷主要包含了小华回家,知道了和就能确定物体的位置等内容,欢迎下载使用。













