2023-2024学年北京市门头沟区七年级（上）期末数学试卷（含详细答案解析）

这是一份2023-2024学年北京市门头沟区七年级（上）期末数学试卷（含详细答案解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.−23的相反数是( )
A. 23B. −32C. 32D. −23
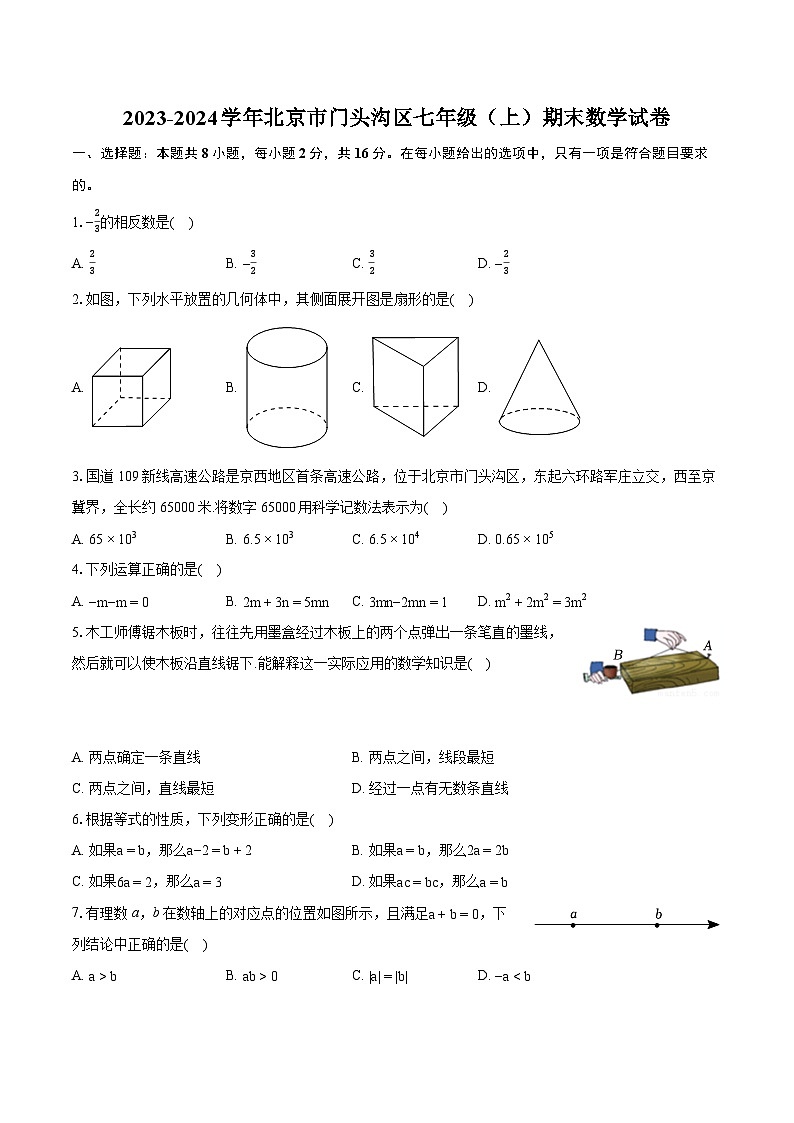
2.如图，下列水平放置的几何体中，其侧面展开图是扇形的是( )
A. B. C. D.
3.国道109新线高速公路是京西地区首条高速公路，位于北京市门头沟区，东起六环路军庄立交，西至京冀界，全长约65000米.将数字65000用科学记数法表示为( )
A. 65×103B. 6.5×103C. 6.5×104D. 0.65×105
4.下列运算正确的是( )
A. −m−m=0B. 2m+3n=5mnC. 3mn−2mn=1D. m2+2m2=3m2
5.木工师傅锯木板时，往往先用墨盒经过木板上的两个点弹出一条笔直的墨线，然后就可以使木板沿直线锯下.能解释这一实际应用的数学知识是( )
A. 两点确定一条直线B. 两点之间，线段最短
C. 两点之间，直线最短D. 经过一点有无数条直线
6.根据等式的性质，下列变形正确的是( )
A. 如果a=b，那么a−2=b+2B. 如果a=b，那么2a=2b
C. 如果6a=2，那么a=3D. 如果ac=bc，那么a=b
7.有理数a，b在数轴上的对应点的位置如图所示，且满足a+b=0，下列结论中正确的是( )
A. a>bB. ab>0C. |a|=|b|D. −a”、“=”或“2560>2320，
∴最省钱的订购方案为：在甲商店订购挂件30个，徽章30个，在乙商店订购徽章70个．
(1)利用在甲商店订购所需费用=挂件每个的标价×购买数量+徽章每个的标价×(购买数量−30)，即可求出结论；
(2)设当订购x(x>30)个徽章时，在甲、乙两家商店分别订购的费用相同，根据在甲、乙两家商店分别订购的费用相同，可列出关于x的一元一次方程，解之即可得出结论；
(3)分别求出在甲商店订购、在乙商店订购及“在甲商店订购挂件30个，徽章30个，在乙商店订购徽章70个”，所需费用，比较后即可得出结论．
本题考查了一元一次方程的应用以及有理数的混合运算，解题的关键是：(1)根据各数量之间的关系，列式计算；(2)找准等量关系，正确列出一元一次方程；(3)根据各数量之间的关系，求出选择各方案所需费用．
27.【答案】20
【解析】解：(1)①如图1中，∵∠AOB=120∘，OC平分∠AOB，
∴∠AOC=12∠AOB=60∘，
∵∠AOD=α，
∴∠DOB=∠AOB−∠AOD=80∘，
∵OE平分∠DOB，
∴∠EOB=12∠DOB=40∘，
∴∠COE=∠AOB−∠AOC−∠EOB=120∘−60∘−40∘=20∘.
故答案为：20；
②如图2中，当∠AOD=α时，∠EOB=12(120∘−α)=60∘−12α，
∴∠COE=∠AOB−∠AOC−∠EOB=120∘−60∘−(60∘−12α)=12α；
(2)如图3中，当OD在OA的下方时，∠COE=60∘+12(360∘−120∘−β)=180∘−12β.
如图4中，当OD在OA的上方时，∠COE=60∘+12(β−120∘)=12β.
综上所述，∠COE=180∘−12β或12β.
(1)①求出∠AOC=60∘，∠EOB=40∘，可得结论；
②求出∠AOC=60∘，∠EOB=12(120∘−α)，可得结论；
(2)分两种情形：如图3中，当OD在OA的下方时，当OD在OA的上方时，分别求解．
本题考查作图-复杂作图，角平分线的定义等知识，解题的关键是学会用分类讨论的射线思考问题．
28.【答案】1 2或−4
【解析】解：(1)∵a=−3，b=a+2，
∴b=−3+2=−1，
∵点M到点P的距离的最小值为点M到线段AB的“到达距离”，且点M与数轴上原点重合时，
∴点M到线段AB的“到达距离”是1，
故答案为：1.
(2)∵点M到线段AB的“到达距离”是2，且点M与数轴上原点重合时，b=a+2，
∴当a=2时，b=4，点M到线段AB的“到达距离”是2，符合题意；
当a=−2时，b=0，点M到线段AB的“到达距离”是0，不符合题意；
当b=2时，a=0，点M到线段AB的“到达距离”是0，不符合题意；
当b=−2时，a=−4，点M到线段AB的“到达距离”是2，符合题意；
综上所述，a=2或a=−4，
故答案为：a=2或a=−4.
(3)当点A对应的数a在−2∼3之间(包含−2，3)时，b=a+2，
∴点b对应的数b在0∼5之间(包含0，5)，
∵点M到线段AB的“到达距离”始终大于3，
∴点M在线段AB外，
这里只考虑两种极限：①当a=−2，b=0时，点M到线段AB的“到达距离”始终大于3，点M在线段AB的左侧，则m−(−2)8；
综上所述，如果点M到线段AB的“到达距离”始终大于3，则m>8或m