2023-2024学年江苏省宿迁市宿城区七年级（上）期末数学试卷（含详细答案解析）

这是一份2023-2024学年江苏省宿迁市宿城区七年级（上）期末数学试卷（含详细答案解析），共16页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.下列各数中为负数的是( )
A. 0B. |−3|C. −22D. −(−3)
2.中国信息通信研究院发布预测称，2025年中国5G用户规模将超过858000000人.将数据858000000用科学记数法表示为( )
A. 8.58×1010B. 8.58×109C. 8.58×108D. 8.58×107
3.下列等式变形中，不正确的是( )
A. 若a=b，则a−2=b−2B. 若a=b，则−2a=−2b
C. 若a=b，则a3=b3D. 若am=bm，则a=b
4.如图是某几何体的表面展开图，该几何体是( )
A. 四棱柱
B. 四棱锥
C. 三棱柱
D. 三棱锥
5.关于代数式x+3，下列说法一定正确的是( )
A. 它的值比x小B. 它的值比3小
C. 它的值比3大D. 它的值随着x的增大而增大
6.泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家，据说“两条直线相交，对顶角相等”就是泰勒斯首次发现并论证的.论证“对顶角相等”使用的依据是( )
A. 同角的余角相等B. 同角的补角相等C. 等角的余角相等D. 等角的补角相等
7.为迎接新年到来，光明中学开展制作“中国结”活动.七(1)班有m人，打算制作n个“中国结”.若每人做4个，则可比计划多做2个；若每人做2个，则将比计划少做58个，现有下列四个方程：
①4m−2=2m+58；②4m+2=2m−58；③n+24=n−582；④n−24=n+582.其中正确的是( )
A. ①③B. ①④C. ②③D. ②④
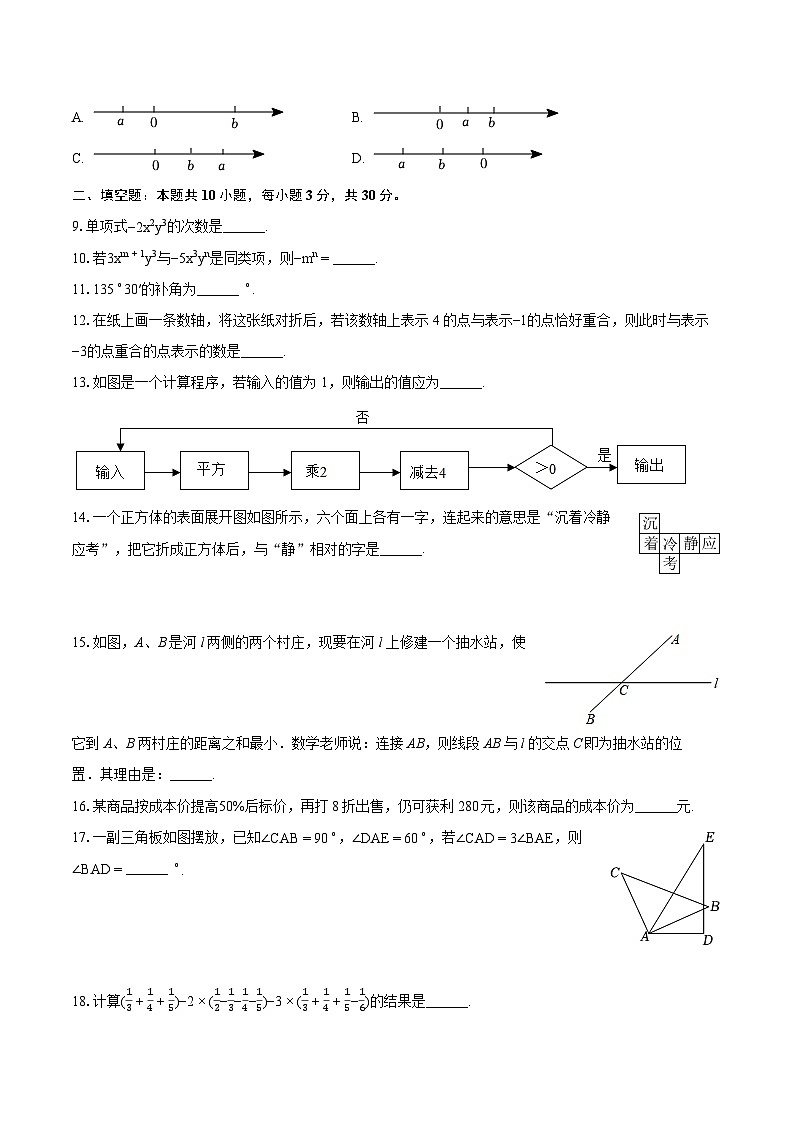
8.若有理数a、b满足等式|b−a|−|a+b|=2b，则有理数数a、b在数轴上的位置可能是( )
A. B.
C. D.
二、填空题：本题共10小题，每小题3分，共30分。
9.单项式−2x2y3的次数是______.
10.若3xm+1y3与−5x3yn是同类项，则−mn=______.
11.135∘30′的补角为______ ∘.
12.在纸上画一条数轴，将这张纸对折后，若该数轴上表示4的点与表示−1的点恰好重合，则此时与表示−3的点重合的点表示的数是______.
13.如图是一个计算程序，若输入的值为1，则输出的值应为______.
14.一个正方体的表面展开图如图所示，六个面上各有一字，连起来的意思是“沉着冷静应考”，把它折成正方体后，与“静”相对的字是______.
15.如图，A、B是河l两侧的两个村庄，现要在河l上修建一个抽水站，使它到A、B两村庄的距离之和最小．数学老师说：连接AB，则线段AB与l的交点C即为抽水站的位置．其理由是：______.
16.某商品按成本价提高50%后标价，再打8折出售，仍可获利280元，则该商品的成本价为______元.
17.一副三角板如图摆放，已知∠CAB=90∘，∠DAE=60∘，若∠CAD=3∠BAE，则∠BAD=______ ∘.
18.计算(13+14+15)−2×(12−13−14−15)−3×(13+14+15−16)的结果是______.
三、计算题：本大题共2小题，共18分。
19.解方程
(1)4(2x−3)−(5x−1)=7
(2)2x−13−5−x6=−2.
20.整理一批图书，由一个人做要40小时完成．现计划由一部分人先做4小时，再增加2人和他们一起做8小时，完成这项工作．假设这些人的工作效率相同，具体应先安排多少人工作？
四、解答题：本题共8小题，共78分。解答应写出文字说明，证明过程或演算步骤。
21.(本小题8分)
计算：
(1)(−1)4−8÷(−4)×|−6+4|；
(2)(−16)×(−34+78−12).
22.(本小题8分)
先化简，再求值：2(3x2y−xy2)−(−xy2+3x2y).其中x=2，y=−1.
23.(本小题8分)
如图是由9个大小相同的小正方体组成的简单几何体.
(1)画出该几何体的三视图；
(2)如果在这个几何体上再添加一些大小相同的小正方体，并保持主视图和俯视图不变，最多可以添加______块小正方体.
24.(本小题10分)
在如图所示的方格纸中，A，B，C为3个格点，点C在直线AB外，
(1)借助格点，过C点画出AB的垂线m和平行线n；
(2)指出(1)中直线m、n的位置关系为______.
(3)连接AC和BC，若图中每个最小正方形的边长为1，则三角形ABC的面积是______.
25.(本小题10分)
如图，线段AB=6cm，延长BA到点C，D是BC的中点.
(1)若AC=4cm，求线段AD的长；
(2)若AC的长逐渐增大，则AD的长的变化趋势是______；
①变小；②变大；③先变小，后变大；④先变大，后变小.
(3)若AD=2cm，求线段AC的长.
26.(本小题10分)
如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD.
(1)如图中与∠COE互补的角是______；(把符合条件的角都写出来)
(2)若∠AOD=15∠EOF，求∠AOD的度数.
27.(本小题12分)
我们规定，关于x的一元一次方程mx=n(m≠0)的解为x=m+n，则称该方程为和解方程，例如2x=−4的解为x=−2=−4+2，则方程为和解方程.
请根据上边规定解答下列问题：
(1)下列关于x的一元一次方程是“和解方程”的有______.
①23x=−23；②−3x=94；③5x=−2.
(2)若关于x的一元一次方程3x=2a−10是和解方程，则a=______.
(3)关于x的一元一次方程3x=a+b是和解方程，则代数式a(a2b+1)+b(1−a3)的值为______.
(4)关于x的一元一次方程3x=a+b是和解方程且它的解为x=a，求代数式2ab(a+b)的值.
28.(本小题12分)
已知，如图1，将一块直角三角板的直角顶点O放置于直线MN上，直角边OA与直线MN重合，其中∠AOB=90∘，然后将三角板AOB.绕点O顺时针旋转，设∠AOM=α，从点O引射线OC和OD，OC平分∠BON，∠BOD=13∠MOB.
(1)如图2，填空：当α=30∘时，∠CON=______ ∘.
(2)如图2，当0∘<α<90∘时，求∠COD的度数(用含α的代数式表示)；
(3)如图3，当90∘<α<180∘时，请判断∠COD−16∠BON的值是否为定值，若为定值，求出该定值，若不是定值，请说明理由.
答案和解析
1.【答案】C
【解析】解：∵0既不是正数也不是负数，
∴A不合题意．
∵−3的绝对值=3>0.
∴B不合题意．
∵−22=−4<0.
∴C符合题意．
∵−(−3)=3>0.
∴D不合题意．
故选：C.
先化简各数，再判断．
本题考查负数的概念，正确化简各选项中的数是求解本题的关键．
2.【答案】C
【解析】解：将数据858000000用科学记数法表示为8.58×108.
故选：C.
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数，当原数绝对值<1时，n是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．
3.【答案】D
【解析】解：A选项考查是等式两边同时加上一个数等式不变，故正确；
B选项考查的是等式两边同时乘以一个数等式不变，故正确；
C选项考查的是等式两边同时除以一个不为0的数等式不变，故正确；
D选项当m=0时，a=b不一定成立，故错误，
故选：D.
根据等式的性质逐个判断即可得到答案．
本题考查等式的性质，解题的关键是熟练掌握几个性质，特别注意除的时候除数不能为0.
4.【答案】D
【解析】解：由该几何体的展开图可知，这个几何体有4个三角形的面，其中1个底面，3个侧面，
因此这个几何体是三棱锥，
故选：D.
根据展开图的面数及形状，再结合几何体的展开图的特征进行判断即可．
本题考查几何体的展开图，理解三棱锥的形体特征是正确解答的前提．
5.【答案】D
【解析】解：A选项，x+3>x，故该选项不符合题意；
B选项，当x=0时，x+3=3，故该选项不符合题意；
C选项，当x=0时，x+3=3，故该选项不符合题意；
D选项，x越大，x+3的值就越大，故该选项符合题意；
故选：D.
根据x+3>x判断A选项；根据特值法判断B，C选项；根据x越大，x+3的值就越大判断D选项．
本题考查了代数式求值，掌握x越大，x+3的值就越大是解题的关键．
6.【答案】B
【解析】解：论证“对顶角相等”使用的依据是：同角的补角相等．
故选：B.
由补角的性质：同角的补角相等，即可判断．
本题考查对顶角，邻补角，补角的性质，关键是掌握：补角的性质．
7.【答案】A
【解析】解：根据题意得：n=4m−2，n=2m+58，
∴4m−2=2m+58，n+24=n−582，
∴方程①③正确．
故选：A.
根据题意可得：n=4m−2，n=2m+58，由n不变可得出4m−2=2m+58，由m不变可得出n+24=n−582，此题得解．
本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．
8.【答案】D
【解析】解：若|b−a|−|a+b|=2b，
则b−a+a+b=2b，
所以b>a且a+b<0，
故选：D.
由|b−a|−|a+b|=2b得到a与b的大小关系，和a+b<0，然后逐个分析即可．
本题考查数轴和绝对值，能够根据准确去绝对值是解答本题的关键．
9.【答案】5
【解析】解：∵单项式的次数是所有字母的指数的和，
∴−2x2y3的次数是5次．
故答案为：5.
单项式的次数是所有字母的指数的和，根据定义解题即可．
本题主要考查单项式的次数，能够熟练运用定义算出次数是解题关键．
10.【答案】−8
【解析】解：∵3xm+1y3与−5x3yn是同类项，
∴m+1=3，n=3，
∴m=2，
∴−mn=−23=−8.
故答案为：−8.
根据同类项的定义得出m+1=3，n=3，求出m，n的值，再代入求出答案即可．
本题考查了同类项的定义，能根据同类项的定义求出m、n的值是解此题的关键．
11.【答案】44.5
【解析】解：由题意得：180∘−135∘30′=44∘30′=44.5∘，
故答案为：44.5.
根据互为余角的和90∘，互补的两角和为180∘，从而计算即可．
本题考查了角的补角和余角及度分秒的转化，解题的关键是理解互为补角的定义．
12.【答案】8
【解析】解解：∵对折后−1和4重合，
∴折痕的位置表示的数为{4−(−1)}÷2=2.5，
设与−3重合的点表示的数为x，则表示x的点和表示−3的点到折痕点2.5的距离相等，
故2.5−(−3)=x−2.5解得x=8，
∴与表示−3的点重合的点表示的数是8，
故答案为：8.
根据题意求出折痕的位置，再利用方程即可求出与−3重合的点表示的数．
本题主要考查数轴的概念，关键是要牢记数轴上两点的中点公式．
13.【答案】4
【解析】解：把1代入得：12×2−4=1×2−4=2−4=−2<0，
把−2代入得：(−2)2×2−4=4×2−4=8−4=4>0，
故输出的值应为4.
故答案为：4.
把1代入计算程序中计算即可得到结果．
此题考查了有理数的混合运算，熟练掌握计算程序和运算法则是解本题的关键．
14.【答案】着
【解析】解：由正方体表面展开图的“相间、Z端是对面”可知，
“静”与“着”是对面，
故答案为：着．
根据正方体表面展开图的特征进行判断即可．
本题考查正方体相对两个面上的文字，掌握正方体表面展开图的特征是正确判断的关键．
15.【答案】两点之间，线段最短．
【解析】解：连接AB，则线段AB与l的交点C即为抽水站的位置．其理由是：两点之间，线段最短．
故答案为：两点之间，线段最短．
根据线段的性质，可得答案．
本题考查了线段的性质，利用线段的性质是解题关键．
16.【答案】1400
【解析】解：设商品的成本价为x元，
由题意得：(1+50%)x⋅80%=x+280，
解得：x=1400.
答：这件商品的成本价为1400元．
故答案为：1400.
首先设商品的成本价为x元，由题意得等量关系：标价×打折=成本价+280元，根据等量关系列出方程即可．
此题主要考查了一元一次方程的应用，关键是正确理解题意，找出题目中的等量关系，再设出未知数，列出方程即可．
17.【答案】22.5
【解析】解：设∠BAD=x∘，则∠BAE=(60−x)∘，∠CAD=(90+x)∘，
根据题意得：90+x=3(60−x)，
解得：x=22.5，
∴∠BAD=x∘=22.5∘.
故答案为：22.5.
设∠BAD=x∘，则∠BAE=(60−x)∘，∠CAD=(90+x)∘，根据∠CAD=3∠BAE，可列出关于x的一元一次方程，解之即可得出结论．
本题考查了角的计算以及解一元一次方程，根据各角之间的关系，正确列出一元一次方程是解题的关键．
18.【答案】−12
【解析】解：设13+14+15=a，
原式=a−2×(12−a)−3×(a−16)
=a−1+2a−3a+12
=−12.
故答案为：−12.
设13+14+15=a，化简求解即可．
此题主要考查有理数的混合运算，解题的关键是根据题意把13+14+15看作一个整体．
19.【答案】解：(1)去括号得：8x−12−5x+1=7，
移项合并得：3x=18，
解得：x=6；
(2)去分母得：2(2x−1)−(5−x)=−12，
去括号得：4x−2−5+x=−12，
移项合并得：5x=−5，
解得：x=−1.
【解析】(1)方程去括号，移项合并，把x系数化为1，即可求出解；
(2)方程去分母，去括号，移项合并，把x系数化为1，即可求出解．
此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．
20.【答案】解：设应先安排x人工作，
根据题意得：4x40+8(x+2)40=1
化简可得：x10+x+25=1，
即：x+2(x+2)=10
解可得：x=2
答：应先安排2人工作．
【解析】由一个人做要40小时完成，即一个人一小时能完成全部工作的140，就是已知工作的速度．本题中存在的相等关系是：这部分人4小时的工作+增加2人后8小时的工作=全部工作．设全部工作是1，这部分共有x人，就可以列出方程．
本题是一个工作效率问题，理解一个人做要40小时完成，即一个人一小时能完成全部工作的140，这一个关系是解题的关键．
21.【答案】解：(1)(−1)4−8÷(−4)×|−6+4|
=1−8÷(−4)×2
=1−(−2)×2
=1−(−4)
=5.
(2)(−16)×(−34+78−12)
=(−16)×(−34)+(−16)×78−(−16)×12
=12−14+8
=6.
【解析】(1)按照先算乘方和绝对值，再算乘除法，最后算减法的顺序来计算；
(2)按照乘法分配律进行简便计算．
本题考查了有理数的混合运算，解题的关键是按照运算顺序进行计算，能简算的要用简便方法计算．
22.【答案】解：原式=6x2y−2xy2+xy2−3x2y
=3x2y−xy2，
当x=2，y=−1时，原式=3×22×(−1)−2×(−1)2=−12−2=−14.
【解析】原式去括号合并得到最简结果，把x与y的值代入计算即可求出值．
此题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．
23.【答案】解：(1)如图，三视图即为所求．
(2)5.
【解析】本题考查作图-三视图，解题的关键是掌握三视图的定义，属于中考常考题型．
(1)根据三视图的定义画出图形即可；
(2)根据要求判断即可．
解：(1)见答案；
(2)如图所示主视图和俯视图不变，俯视图中可添加小正方体：2+2+1=5，最多可以添加5块小正方体．
故答案为：5.
24.【答案】m⊥n6
【解析】解：(1)如图，直线m，直线n即为所求；
(2)∵m⊥AB，n//AB，
∴m⊥n，
故答案为：m⊥n；
(3)S△ABC=12×4×3=6，
故答案为：6.
(1)利用数形结合的思想以及垂线，平行线的定义作出图形即可；
(2)利用垂线的判定方法解决问题；
(3)根据三角形面积公式求解即可．
本题考查作图-应用与设计作图，平行线的判定和性质，三角形的面积等知识，解题的关键是掌握垂线，平行线的定义，属于中考常考题型．
25.【答案】③
【解析】解：(1)∵AB=6cm，AC=4cm，
∴BC=AB+AC=6+4=10(cm)，
∵D是BC的中点，
∴CD=12BC=12×10=5(cm)，
∴AD=CD−AC=5−4=1(cm)，
∴线段AD的长为1cm；
(2)∵随着AC的变长，D越来越靠近点A，当AC=AB是点D与A 重合，然后点D离点A越来越远，
故选：③；
(3)解：Ⅰ当点D在AB上时
∵AB=6cm，AD=2cm，
∴BD=AB−AD=6−2=4(cm)，
∵D是BC的中点，
∴BC=2BD=2×4=8(cm)，
∴AC=BC−AB=8−6=2(cm)；
Ⅱ当点D在BA延长线上时，
∵AB=6cm，AD=2cm，
∴BD=AB+AD=6+2=8(cm).
∵D是BC的中点，
∴BC=2BD=2×8=16(cm)，
∴AC=BC−AB=16−6=10(cm).
(1)求出线段AC的长度，除以2即可；
(2)点D有左向右越来越靠近点A，然后远离点A，所以先变小后变大；
(3)求出BD的长，进而求出BA的长，做减法即可．
本题考查的是两点间的距离，解题的关键是会求线段的和、差、倍、分．
26.【答案】解：(1)∠EOD，∠AOF；
(2)设∠AOD=x，则∠EOF=5x，∠EOC=90∘−x，
因为∠AOD=∠BOC(对顶角相等)，
所以∠EOF=∠EOC+∠COF=90∘+90∘−x=5x，
即6x=180∘，
解得：x=30∘.
所以∠AOD=30∘.
【解析】解：(1)因为∠COE+∠EOD=180∘，
所以∠EOD与∠COE互补，
所以与∠COE互补的角是：∠EOD.
因为∠AOE=∠DOF，所以∠EOD=∠AOF
故答案为：∠EOD，∠AOF.
(2)见答案.
(1)根据互补的两个角的和等于180∘，结合图形找出与∠COE的和等于180∘的角即可；
(2)设∠AOD=x，可以得到∠EOF=5x，然后列式求解即可．
本题考查了补角的和等于180∘的性质，以及对顶角相等，周角等于360∘的性质，结合图形找出各角的关系是解题的关键．
27.【答案】② 114 −92
【解析】解：(1)①23x=−23的解是x=−1≠23−23，故不是“和解方程”；
②−3x=94的解是x=−34=−3+94，故是“和解方程”；
③5x=−2的解是x=−25≠5−2，故不是“和解方程”；
故答案为：②；
(2)∵3x=2a−10是和解方程，
∴x=2a−103=3+2a−10，
解得：a=114，
故答案为：114；
(3)∵3x=a+b是和解方程，
∴x=a+b3=3+a+b，
化简得：a+b=−92，
∴a(a2b+1)+b(1−a3)=a3b+a+b−a3b=a+b=−92，
故答案为：−92；
(4)∵3x=a+b是和解方程且它的解为x=a，
∴x=a+b3=3+a+b=a，
∴解得：a=−32，b=−3，
∴2ab(a+b)=2×(−32)×(−3)[(−32)+(−3)]=−812.
(1)根据“和解方程”的定义进行判断即可；
(2)根据“和解方程”的定义得到关于a的方程，解之即可；
(3)根据“和解方程”的定义得到a+b=−92，将所求式子化简后整体代入即可；
(4)根据已知条件得到x=a+b3=3+a+b=a，可求出a，b值，代入计算即可．
本题考查了一元一次方程的解，代数式求值，掌握解一元一次方程的步骤是解题的关键．
28.【答案】解：(1)30；
(2)当0∘<α<90∘时，
因为∠AOM=α，∠AOB=90∘，
所以∠BON=∠MON−∠AOM−∠AOB=180∘−α−90∘=90∘−α，
因为OC平分∠BON，
所以∠BOC=12(90∘−α)，
因为∠MOB=∠MOA+∠AOB=90∘+α，
所以∠BOD=13(90∘+α)，
所以∠COD=∠BOD+∠BOC=13(90∘+α)+12(90∘−α)=75∘−16α；
(3)是定值，
当90∘<α<180∘时，
因为∠BOM=360∘−90∘−α=270∘−α，
所以∠BOD=13∠BOM=13(270∘−α)=90∘−13α，
因为OC平分∠BON，∠BON=90∘+α−180∘=α−90∘，
所以∠COB=12∠BON=12(α−90∘)=12α−45∘，
所以∠COD=∠BOD+∠COB=(90∘−13α)+(12α−45∘)=16α+45∘，
所以∠COD−16∠BON=(16α+45∘)−16(α−90∘)=60∘.
【解析】(1)因为OC平分∠BON，
所以∠CON=12∠BON，
因为∠BON=180∘−∠AOB−∠α=180∘−90∘−30∘=60∘，
所以∠CON=30∘，
故答案为：30；
(2)见答案；
(3)见答案．
(1)利用平角和角平分线计算即可；
(2)由角平分线定义，平角定义求出∠BOD和∠BOC即可求出∠COD；
(3)利用已知条件和等量关系分别求出∠COD和∠BON，代入∠COD−16∠BON计算即可．
本题考查余角、补角、角平分线，关键是掌握余角、补角、角平分线的定义．