2023-2024学年江苏省徐州市七年级（上）期末数学试卷（含详细答案解析）

这是一份2023-2024学年江苏省徐州市七年级（上）期末数学试卷（含详细答案解析），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.2024的相反数是( )
A. 2024B. −2024C. 12024D. −12024
2.下列各图中，不是正方体的展开图的是( )
A. B. C. D.
3.下列计算正确的是( )
A. 7a+a=8a2B. 5y−3y=2
C. 3x2y−2x2y=x2yD. 3a+2b=5ab
4.下列去括号正确的是( )
A. −(a+b)=−a+bB. −2(a−b)=−2a+2b
C. a−(b+c)=a+b−cD. a−3(b−c)=a−3b+c
5.如图，用大小相同的正方体积木搭成一个几何体，若拿走其中的一块积木，该几何体的主视图会发生变化，则被拿走的积木可能是( )
A. 甲
B. 乙
C. 丙
D. 丁
6.如图，已知数轴上点A对应的数为a，则下列结论正确的是( )
A. −2<−aC. −a<−2<27.下列代数式，满足表中条件的是( )
A. −x−3B. x2+2x−3C. 2x−3D. x2−2x−3
8.已知A、B、C三点在同一直线上，若AB=20，AC=30，则BC的长度为( )
A. 10B. 50C. 25D. 10或50
二、填空题：本题共8小题，每小题4分，共32分。
9.请你写出一个无理数______.
10.某日最低气温是−4℃，最高气温是1℃，则该日的温差为______ ℃.
11.2023年12月31日，徐州地铁客流量首次突破600000人次，600000人次用科学记数法可表示为______人次.
12.将一根细木条固定在墙上，至少需要两根钉子，理由：______.
13.单项式−5xy2的次数是______.
14.若∠α=23∘，则∠α的补角为______ ∘.
15.已知代数式x+2y的值是2，则代数式1−2x−4y的值是______.
16.用长度相同的小棒，按如图所示的规律拼图，则第n个图案需用小棒______根.
三、解答题：本题共9小题，共84分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题10分)
计算：
(1)−7+4+(−5)−(−18)；
(2)−12+16×[−3+(−3)2].
18.(本小题8分)
先化简，再求值：x−(2x2−4xy)+2(x2−xy)，其中x=1,y=12.
19.(本小题10分)
解下列方程：
(1)4x+5=x−1；
(2)x−32−x+56=1.
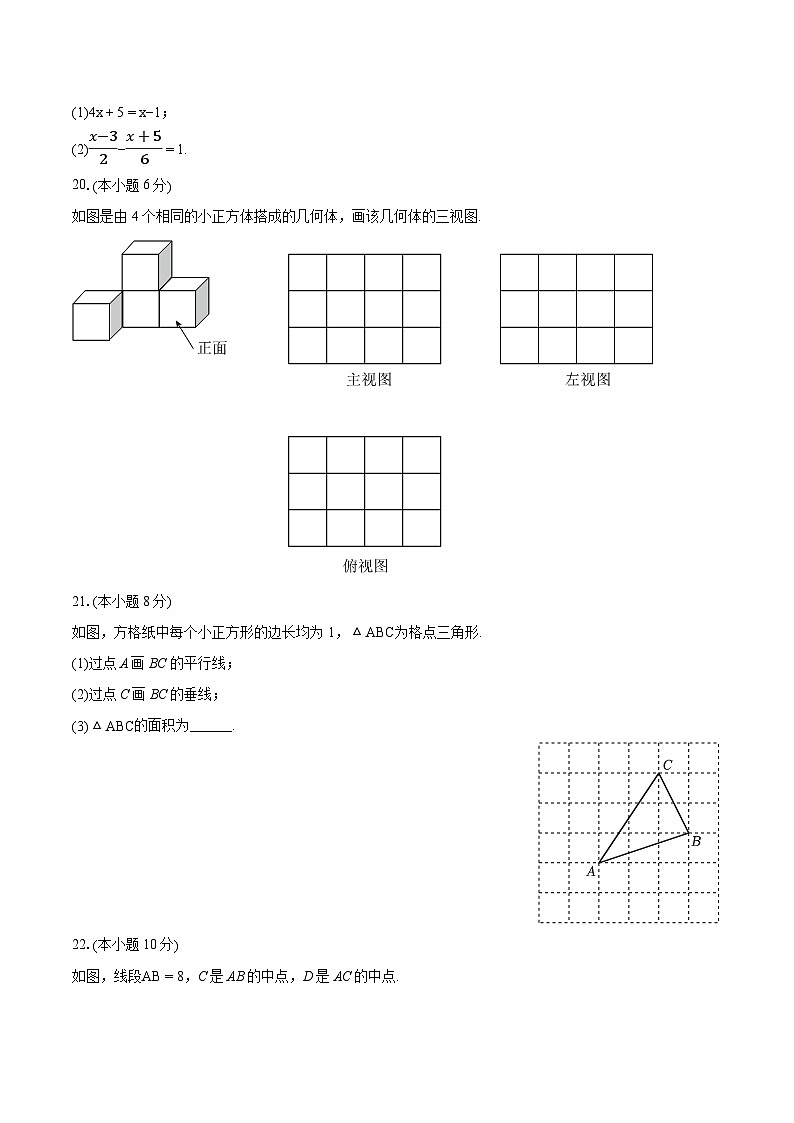
20.(本小题6分)
如图是由4个相同的小正方体搭成的几何体，画该几何体的三视图.
21.(本小题8分)
如图，方格纸中每个小正方形的边长均为1，△ABC为格点三角形.
(1)过点A画BC的平行线；
(2)过点C画BC的垂线；
(3)△ABC的面积为______.
22.(本小题10分)
如图，线段AB=8，C是AB的中点，D是AC的中点.
(1)求线段AD的长度；
(2)若点E在AB上，CE=14BC，求线段AE的长度.
23.(本小题10分)
如图，点O在直线AB上，∠COE=90∘，OF平分∠AOE.
(1)若∠COF=57∘，求∠BOE的度数；
(2)若∠COF=α，则∠BOE=______.(用含α的式子表示)
24.(本小题10分)
为筹备文艺会演，七(1)班计划在某店铺购买甲、乙两种演出道具，已知该店铺甲道具每件标价10元，乙道具每件标价2元，现有以下两个促销方案：
(1)若购买10件甲道具与30件乙道具，则两个方案所需的费用相差多少元？
(2)若购买甲道具的件数比乙道具少20件时，两个方案所需的费用相同，则此时购买两种道具各多少件？
25.(本小题12分)
在同一平面内有n条直线，设它们的交点个数为m.
例如：当n=2时，m=0或m=1(如图所示).
(1)当n=3时，m可以取哪些不同的值？请画图说明；
(2)当n=4时，m的最大值为多少？请画图说明；
(3)m的最大值为______；(用含n的式子表示)
(4)当m=6时，n的最大值为多少？请画图说明.
答案和解析
1.【答案】B
【解析】解：2024的相反数是−2024，
故选：B.
根据只有符号不同的两个数互为相反数进行解答即可得．
本题考查了相反数的定义，熟练掌握相反数的定义是解题的关键．
2.【答案】C
【解析】解：正方体共有11种表面展开图，
A、B、D能围成正方体；
C、出现了“田”字不能折成正方体．
故选C.
根据平面图形的折叠及正方体的展开图解题，只要有“田”字格的展开图都不是正方体的表面展开图．
本题考查的是学生的立体思维能力．解题时勿忘记四棱柱的特征及正方体展开图的各种情形．
3.【答案】C
【解析】解：A.7a+a=8a，故本选项不合题意；
B.5y−3y=2y，故本选项不合题意；
C.3x2y−2x2y=x2y，故本选项符合题意；
D.3a与2b不是同类项，所以不能合并，故本选项不合题意．
故选：C.
合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变．据此判断即可．
本题考查了合并同类项，掌握合并同类项法则是解答本题的关键．
4.【答案】B
【解析】解：A.−(a+b)=−a−b，结论错误，故不符合题意；
B.−2(a−b)=−2a+2b，结论正确，故符合题意；
C.a−(b+c)=a−b−c，结论错误，故不符合题意；
D.a−3(b−c)=a−3b+3c，结论错误，故不符合题意．
故选：B.
根据法则：“括号前面是+，去括号时，括号里的各项不变号；括号前面是-，去括号时，括号里的各项都变号．”进行判断．
本题考查了去括号法则，掌握法则：“括号前面是+，去括号时，括号里的各项不变号；括号前面是-，去括号时，括号里的各项都变号．”是解题的关键．
5.【答案】B
【解析】解：拿走图中的“乙”一个积木后，此图形主视图的形状会改变，第二列小正方形的个数由原来的两个变成一个．
故选：B.
根据从前面看得到的图象是主视图，可得答案．
此题主要考查了简单几何体的三视图，关键是掌握主视图所看的位置．
6.【答案】C
【解析】解：由数轴得，a>2，
∴−a<−2，
∴−a<−2<2故选：C.
由数轴得a>2，根据相反数的意义可知−a<−2，从而得出−a<−2<2本题考查了数轴，有理数的大小比较，熟练掌握数形结合思想的应用是解题的关键．
7.【答案】C
【解析】解：∵x=0时，y=−3；x=1时，y=−1；x=2时，y=1，
∴只有2x−3满足此条件．
故选：C.
根据图表中数据进而代入求出即可．
此题主要考查了代数式求值，正确利用代数式求值的方法得出是解题关键．
8.【答案】D
【解析】解：如图1，当点C在AB延长线上时，
BC=AC−AB，
∵AB=20，AC=30，
∴BC=30−20=10；
如图2，当点C在BA延长线上时，
BC=AC+AB，
∵AB=20，AC=30，
∴BC=30+20=50；
∴BC的长度为10或50.
故选：D.
分点C在AB延长线上和分点C在BA延长线上分别画图进行计算即可求出BC的长度．
本题主要考查线段的和差计算，熟练掌握分类讨论的数学思想是解决问题的关键．
9.【答案】π(答案不唯一)
【解析】解：由题意可得，π是无理数．
故答案可为：π.(答案不唯一)
①开方开不尽的数，②无限不循环小数，③含有π的数，由此可写出答案．
此题考查了无理数的定义，关键是掌握无理数的三种形式，①开方开不尽的数，②无限不循环小数，③含有π的数，比较简单．
10.【答案】5
【解析】解：1−(−4)=1+4=5℃.
故答案为：5.
用最高气温减去最低气温，然后根据减去一个数等于加上这个数的相反数进行计算即可得解．
本题考查了有理数的减法，是基础题，熟记减去一个数等于加上这个数的相反数是解题的关键．
11.【答案】6×105
【解析】解：600000=6×105，
故答案为：6×105.
将一个数表示成a×10n的形式，其中1≤|a|<10，n为整数，这种记数方法叫做科学记数法，据此即可求得答案．
本题考查科学记数法表示较大的数，熟练掌握其定义是解题的关键．
12.【答案】两点确定一条直线
【解析】解：在墙上固定一根木条至少需要两根钉子，依据的数学道理是两点确定一条直线．
故答案为：两点确定一条直线．
由于两点确定一条直线，所以在墙上固定一根木条至少需要两根钉子．
此题主要考查了直线的性质，在生活中，用数学原理“两点确定一条直线”的事物有很多，应注意体会．如晒衣服的杆子，打台球．
13.【答案】3
【解析】解：根据单项式的定义，单项式−5xy2的次数是3.
故答案为：3.
根据单项式次数的定义解决此题．
本题主要考查单项式，熟练掌握单项式的定义是解决本题的关键．
14.【答案】157
【解析】解：若∠α=23∘，则∠α的补角为：180∘−23∘=157∘.
故答案为：157.
根据互为补角的两个角的和等于180∘列式进行计算即可得解．
本题主要考查了补角，熟记补角的定义是解答本题的关键．
15.【答案】−3
【解析】解：∵x+2y=2，
∴1−2x−4y=1−2(x+2y)=1−2×2=−3.
故答案为：−3.
将1−2x−4y变形为1−2(x+2y)，再整体代入即可．
本题考查了整式的代数式求值，整体代入是解题的关键．
16.【答案】(5n+9)
【解析】解：由所给图形可知，
第1个图案需用的小棒根数为：14=1×5+9；
第2个图案需用的小棒根数为：19=2×5+9；
第3个图案需用的小棒根数为：24=3×5+9；
…，
所以第n个图案需用的小棒根数为(5n+9)根．
故答案为：(5n+9).
依次求出图形中小棒的根数，发现规律即可解决问题．
本题考查图形变化的规律，能根据所给图形发现小棒的根数依次增加5是解题的关键．
17.【答案】解：(1)原式=−3−5+18
=10；
(2)原式=−1+16×(−3+9)
=−1+16×6
=−1+1
=0.
【解析】(1)利用有理数的加减法则计算即可；
(2)先算乘方及括号里面的，再算乘法，最后算加法即可．
本题考查有理数的混合运算，熟练掌握相关运算法则是解题的关键．
18.【答案】解：原式=x−2x2+4xy+2x2−2xy
=x+2xy；
当x=1，y=12时，
原式=1+2×1×12=1+1=2.
【解析】将原式去括号，合并同类项后代入数值计算即可．
本题考查整式的化简求值，熟练掌握相关运算法则是解题的关键．
19.【答案】解：(1)移项得：4x−x=−1−5，
合并同类项得：3x=−6，
解得：x=−2；
(2)去分母得：3(x−3)−(x+5)=6，
去括号得：3x−9−x−5=6，
移项得：3x−x=6+9+5，
合并同类项得：2x=20，
解得：x=10.
【解析】(1)方程移项，合并同类项，把x系数化为1，即可求出解；
(2)方程去分母，去括号，移项，合并同类项，把x系数化为1，即可求出解．
此题考查了解一元一次方程，熟练掌握一元一次方程的解法是解本题的关键．
20.【答案】解：如图所示．

【解析】根据三视图的定义画图即可．
本题考查作图-三视图，解题的关键是理解三视图的定义，难度不大．
21.【答案】3.5
【解析】解：(1)EF即为所求；
(2)AH即为所求；
(3)△ABC的面积为：3×3−12×1×3−12×1×2−12×2×3=3.5，
故答案为：3.5.
(1)根据网格线的特点及平行线的性质作图；
(2)根据网格线的特点及垂线的性质作图；
(3)根据割补法求解．
本题考查了作图的应用与设计，掌握网格线的特点及割补法是解题的关键．
22.【答案】解：(1)∵C是AB的中点，D是AC的中点，
∴AC=12AB，AD=12AC，
∴AD=14AB，
∵AB=8，
∴AD=14AB=2；
(2))∵C是AB的中点，AB=8，
∴AC=BC=12AB=4，
∵CE=14BC，
∴CE=1，
当点E在线段AC上时，AE=AC−CE=4−1=3；
当点E在线段BC上时，AE=AC+CE=4+1=5；
综上所述，线段AE的长度为3或5.
【解析】(1)先根据中点定义推出AC=12AB，AD=12AC，从而得到AD=14AB，根据AB的长度即可求出AD的长度；
(2)分两种情况：①点E在线段AC上；②点E在线段BC上．求出CE的长度后用AC的长减去CE或者加上CE即可求出线段AE的长度．
本题主要考查线段的和差倍分计算，熟练掌握线段中点定义和分类讨论的数学思想是解决问题的关键．
23.【答案】2α
【解析】解：(1)∵∠COE=90∘，∠COF=57∘，
∴∠EOF=90∘−57∘=33∘，
∵OF平分∠AOE，
∴∠AOE=2∠EOF=66∘，
∴∠BOE=180∘−66∘=114∘；
(2)∵∠COE=90∘，∠COF=α，
∴∠EOF=90∘−α，
∵OF平分∠AOE，
∴∠AOE=2∠EOF=180∘−2α，
∴∠BOE=180∘−(180∘−2α)=2α.
故答案为：2α.
(1)先用∠COE的度数和减去∠COF的度数求出∠EOF的度数，然后根据角平分线定义求出∠AOE等于∠EOF的2倍，最后根据邻补角定义即可求出∠BOE的度数；
(2)根据(1)的方法先用∠COE的度数和减去∠COF的度数求出∠EOF的度数，然后根据角平分线定义求出∠AOE等于∠EOF的2倍，最后根据邻补角定义即可用含α的代数式表示出∠BOE的度数．
本题主要考查角的计算和角平分线定义，熟练掌握角的和差倍分的计算方法是解决问题的关键．
24.【答案】解：(1)选择方案一所需费用为10×10+2×(30−10)=140(元)，
选择方案二所需费用为10×0.9×10+2×0.9×30=144(元)，
∴144−140=4(元).
答：两个方案所需的费用相差4元；
(2)设此时购买x件甲道具，则购买(x+20)件乙道具，
根据题意得：10x+2(x+20−x)=10×0.9x+2×0.9(x+20)，
解得：x=5，
∴x+20=5+20=25(件).
答：此时购买5件甲道具，25件乙道具．
【解析】(1)利用总价=单价×数量，结合该店铺给出的优惠方案，可分别求出选择方案一及选择方案二所需费用，作差后即可得出结论；
(2)设此时购买x件甲道具，则购买(x+20)件乙道具，根据选择两个方案所需的费用相同，可列出关于x的一元一次方程，解之即可得出结论．
本题考查了一元一次方程的应用以及有理数的混合运算，解题的关键是：(1)根据各数量之间的关系，列式计算；(2)找准等量关系，正确列出一元一次方程．
25.【答案】12n(n−1)
【解析】解：(1)当n=3时，即三条直线相交，交点的个数为0个或1个或2个或3个．
如图1所示：

(2)当n=4时，即四条直线相交，交点最多是6个，
∴m的最大值为6，如图2所示：

∴四条直线最多有6个交点，
∴m的最大值为6.
(3)由(1)可知：三条直线相交，交点最多是1+2=3(个)；
由(2)可知：四条直线相交，交点最多是1+2+3=6(个)；
画图不难得到：五条直线相交，交点最多是1+2+3+4=10(个)；
六条直线相交，交点最多是1+2+3+4+5=15(个)；
…，以此类推，n条直线相交，交点最多是1+2+3+4+…+(n−1)=12n(n−1)(个)，
故答案为：12n(n−1)；
(4)当m=6时，n的最大值为7，如图3所示：

(1)通过画图即可得出答案；
(2)通过画图即可得出答案；
(3)根据(1)(2)及画图可得三条直线相交，交点最多是1+2=3(个)；四条直线相交，交点最多是1+2+3=6(个)；五条直线相交，交点最多是1+2+3+4=10(个)；六条直线相交，交点最多是1+2+3+4+5=15(个)；…，以此类推，n条直线相交，最多交点的个数；
(4)当当m=6时，画图可得出答案．
此题主要考查了平行线与相交线，理解在同一平面内永不相交的直线叫做平行线，两条直线相交有且只有一个交点是解决问题的关键．x
0
1
2
3
代数式的值
−3
−1
1
3
方案一：买一送一(每买一件甲道具，送一件乙道具)
方案二：全场九折(即全部商品按标价的九折销售)