2023-2024学年浙江省绍兴市新昌县七年级（上）期末数学试卷（含详细答案解析）

这是一份2023-2024学年浙江省绍兴市新昌县七年级（上）期末数学试卷（含详细答案解析），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.−2024的倒数是( )
A. 2024B. −2024C. 12024D. −12024
2.某自动控制器的芯片，可植入2020000000粒晶体管，这个数字2020000000用科学记数法可表示为( )
A. 0.202×1010B. 2.02×109C. 20.2×108D. 2.02×108
3.在数4，−1，3，−6中，最小的数是( )
A. 4B. −1C. 3D. −6
4.估计68的立方根的大小在( )
A. 2与3之间B. 3与4之间C. 4与5之间D. 5与6之间
5.用计算器进行计算，按下列按键顺序输入：
，则它表达的算式正确的是( )
A. −32−56B. (−3)2−56C. −32−65D. (−3)2−5×6
6.把方程0.1−0.2x0.3−1=0.5−x0.4的分母化为整数，结果应为( )
A. 01−0.2x3−1=0.5−x4B. 1−2x3−1=5−10x4
C. 1−2x3−10=5−10x4D. 1−2x3−1=5−x4
7.如图，直线AB、CD相交于点E，EF⊥AB于E，若∠CEF=65∘，则∠DEB的度数为( )
A. 155∘B. 135∘C. 35∘D. 25∘
8.用刻度尺画数轴时，刻度尺上的2.5cm处对应数轴上的原点，3cm处对应数轴上的1，则数轴上表示3的点对应刻度尺上的刻度是( )
A. 5cmB. 4cmC. 3cmD. 2.5cm
9.甲乙丙三位同学合乘一辆滴滴车去顺路的三个地点，事先约定三人根据路程分摊车费，甲在全程的四分之一处下车，甲下车时，乙离下车点还有一半的路程，丙坐完全程.已知乙支付了18元车费，则三人一共支付多少车费？( )
A. 36元B. 48元C. 63元D. 81元
10.如图，点O在直线AB上，点A1A2A3，…，在射线OA上，点B1B2B3…，在射线OB上，图中相邻的点之间的距离为1.一个动点M从O点出发，以每秒1个单位长度的速度，按如图所示的箭头方向，沿着实线段和以点O为圆心的半圆匀速运动，即从O→A1→B1→B2→A2→A3=B1→B4…，按此规律，则动点M到达A10点处所需时间为秒.( )
A. 10+55πB. 20+55πC. 10+110πD. 20+110π
二、填空题：本题共6小题，每小题3分，共18分。
11. 2的相反数是__________.
12.已知∠α=26∘，则∠α的补角是______度.
13.“x的2倍与y的和”用代数式表示为______.
14.如图，直线l表示一段河道，点P表示村庄，现要从河l向村庄P引水，图中有四种方案，其中沿线段PC路线开挖的水渠长最短，理由是______.
15.根据下表中的数据，求得a的值为______.
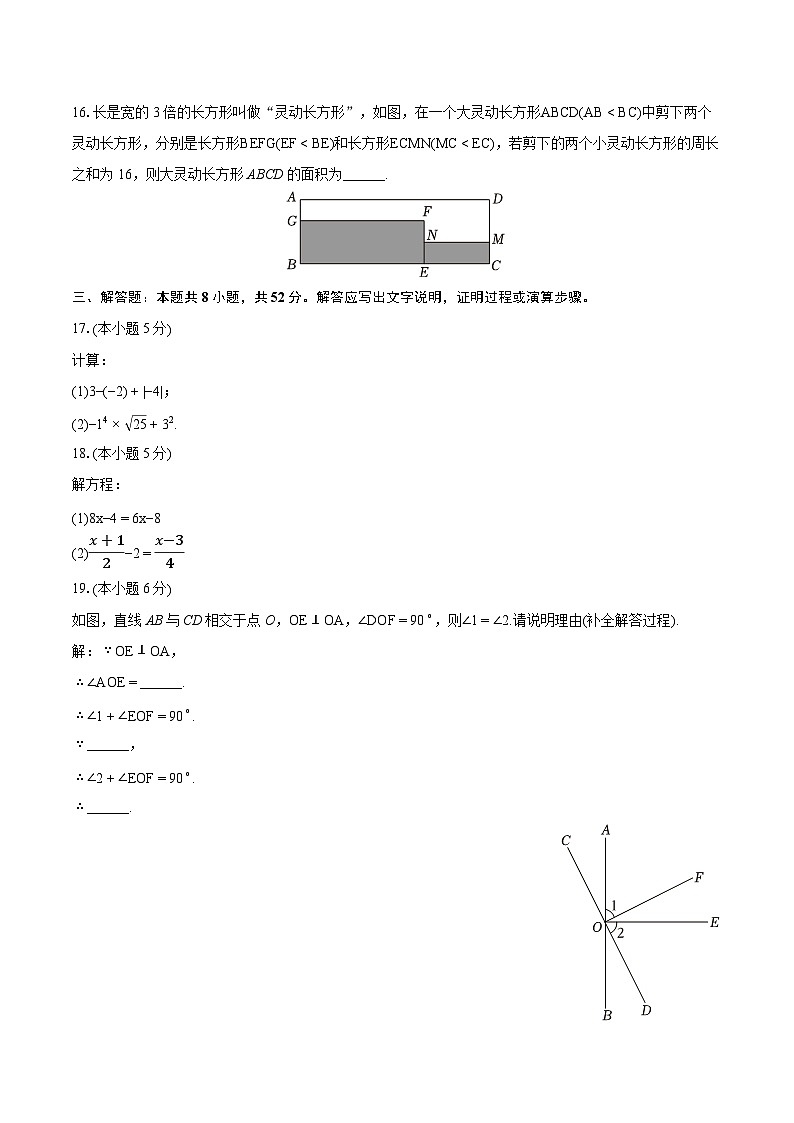
16.长是宽的3倍的长方形叫做“灵动长方形”，如图，在一个大灵动长方形ABCD(AB三、解答题：本题共8小题，共52分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题5分)
计算：
(1)3−(−2)+|−4|；
(2)−14× 25+32.
18.(本小题5分)
解方程：
(1)8x−4=6x−8
(2)x+12−2=x−34
19.(本小题6分)
如图，直线AB与CD相交于点O，OE⊥OA，∠DOF=90∘，则∠1=∠2.请说明理由(补全解答过程).
解：∵OE⊥OA，
∴∠AOE=______.
∴∠1+∠EOF=90∘.
∵______，
∴∠2+∠EOF=90∘.
∴______.
20.(本小题6分)
化简求值：2(3a2b−ab2)−3(a2b+1−2ab2)+3，其中a=3，b=−3.
21.(本小题6分)
已知线段AB=6cm，延长AB至点C，使AB=2BC，D是线段AC的中点.求线段DB的长.
22.(本小题6分)
如图，一个长方体玻璃容器的内底面长为8cm，宽为6cm，高为16cm，容器内水的高度为2cm，现把一块边长为4cm的立方体金属块放入水中，问容器内的水将升高多少厘米？
23.(本小题8分)
如图，点O是直线AE上的一点，OC是∠AOD的平分线，∠BOD=13∠AOD.
(1)若∠AOD=60∘，求∠BOC的度数.
(2)若∠BOC=n∘，用含有n的代数式表示∠AOD的大小.
24.(本小题10分)
如图，某动力科学研究实验基地内装有一段长为91m的笔直轨道AB，现将长度为1m的金属滑块在上面往返滑动一次，滑动开始前，滑块左端与点A重合，滑动过程由三个阶段组成：
1、滑块以9m/s的速度沿AB方向匀速滑动，当滑块的右端与点B重合时，滑动停止.
2、滑块停顿2s.
3、滑块以小于9m/s的速度沿BA方向匀速返回，当滑块的左端与点A重合时，滑动停止.
设滑动时间为t(s)时，滑块左端离点A的距离为l1(m)，右端离点B的距离为l2(m).
(1)当t=10s时，求l1的值.
(2)整个滑动过程总用时27s(含停顿的时间)，请根据所给条件解决下列问题：
①求滑块返回的速度.
②记d=l1−l2，若d=18m，求t的值.
答案和解析
1.【答案】D
【解析】解：−2024的倒数是−12024；
故选：D.
乘积是1的两数互为倒数．据此解答即可．
本题考查了倒数，掌握倒数的定义是解答本题的关键．
2.【答案】B
【解析】【分析】
本题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．
根据科学记数法的表示方法解答即可.
【解答】
解：2020000000=2.02×109，
故选：B.
3.【答案】D
【解析】解：∵1<6，
∴−1>−6.
∴−6<−1<3<4.
∴在数4，−1，3，−6中，最小的数是−6.
故选：D.
依据正数大于零，负数小于零，正数大于一切负数，两个负数绝对值大的反而小进行比较即可．
本题主要考查的是比较有理数的大小，熟练掌握相关法则是解题的关键．
4.【答案】C
【解析】解：∵43=64，53=125，
而64<68<125，
∴4<368<5.
故选：C.
由于43=64，53=125，所以68的立方根在4和5之间，由此即可判定选择项．
此题主要考查了无理数的估算，需掌握三次根式的基本运算技能，灵活应用．“夹逼法”是估算的一般方法，也是常用方法．
5.【答案】A
【解析】解：按下列按键顺序输入：，则它表达的算式是−32−56，
故选：A.
根据计算器的使用方法，结合各项进行判断即可．
此题主要考查了计算器的应用，属于基础题．
6.【答案】B
【解析】解：0.1−0.2x0.3−1=0.5−x0.4，
化简得：1−2x3−1=5−10x4.
故选：B.
根据分数的基本性质进行变形即可．
本题考查了解一元一次方程和分数的基本性质，能正确根据分数的基本性质进行变形是解此题的关键．
7.【答案】D
【解析】【分析】
此题主要考查了垂线以及对顶角，正确得出∠AEC的度数是解题关键.
直接利用垂直的定义结合互余的性质、对顶角的性质得出答案.
【解答】
解：∵EF⊥AB于E，∠CEF=65∘，
∵∠AEF=90∘，
∴∠AEC=∠BED=90∘−65∘=25∘.
故选D.
8.【答案】B
【解析】解：根据题意，刻度尺上的2.5cm处对应数轴上的原点，3cm处对应数轴上的1，
则该数轴的1个单位长度为：(3−2.5)÷1=0.5(cm)，
所以，数轴上表示3的点对应刻度尺上的刻度是2.5+3×0.5=4(cm).
故选：B.
首先根据题意求得数轴的1个单位长度为0.5cm，然后计算数轴上表示3的点对应刻度尺上的刻度即可．
本题主要考查数轴的知识，确定数轴上1个单位的具体长度是解题关键．
9.【答案】C
【解析】解：由题意得甲乙丙三人的路程比为1：2：4，
∴三人一共支付车费18÷21+2+4=63(元)，
故选：C.
根据题意得到甲乙丙的路程比，即可求得总车费．
本题考查分数除法的应用，能够理解题意，读懂题意是解题的关键．
10.【答案】A
【解析】解：动点M从O点出发到A4点，在直线AB上运动了4个单位长度，在以O为圆心的半圆运动了(π⋅1+π⋅2+π⋅3+π⋅4)单位长度，
∵10=4×2.5，
∴动点M到达A10点处运动的单位长度=4×2.5+(π⋅1+π⋅2+…+π⋅10)=10+55π；
∴动点M到达A10点处运动所需时间=(10+55π)÷1=(10+55π)秒．
故选：A.
观察动点M从O点出发到A4点，得到点M在直线AB上运动了4个单位长度，在以O为圆心的半圆运动了(π⋅1+π⋅2+π⋅3+π⋅4)单位长度，然后可得到动点M到达A10点处运动的单位长度=4×2.5+(π⋅1+π⋅2+…+π⋅10)，然后除以速度即可得到动点M到达A10点处所需时间．
此题主要考查了图形的变化类：通过特殊图象找到图象变化，归纳总结出运动规律，再利用规律解决问题．也考查了圆的周长公式．
11.【答案】− 2
【解析】【分析】
本题考查相反数的定义，解题的关键是熟练运用相反数的定义，属于基础题．
根据相反数的定义即可求出答案．
【解答】解： 2的相反数是− 2，
故答案为：− 2.
12.【答案】154
【解析】解：∵∠α=26∘，
∴∠α的补角是：180∘−26∘=154∘，
故答案为154.
根据互补两角的和为180∘，即可得出结果．
本题考查了互补两角的和为180∘，比较简单．
13.【答案】2x+y
【解析】解：“x的2倍与y的和”用代数式表示为：2x+y.
故答案为2x+y.
首先求得x的2倍为2x，再求“与y的和”即可得出代数式．
此题考查列代数式，理解题意，掌握计算方法是解决问题的关键．
14.【答案】垂线段最短
【解析】解：沿线段PC路线开挖的水渠长最短，理由是垂线段最短．
故答案为：垂线段最短．
根据“垂线段最短”进行解答即可．
本题考查垂线段最短，理解“从直线外一点，到直线上任意一点所引的线段中，垂直线段最短”是正确解答的关键．
15.【答案】3
【解析】解：当x=n时，3x+1=4，即3n+1=4，
解得：n=1，
当x=1时，2x+1x=a，即2×1+11=a，
∴a=3，
故答案为：3.
把x=n代入3x+1=4解得n，再代入2x+1x=a求解即可．
本题考查了求代数式的值，解一元一次方程，解题的关键是正确运算．
16.【答案】12
【解析】解：设EF=m，MC=n，
∴BG=EF=m，BE=GF=3m，NE=MC=n，MN=EC=3n，
∴2EF+2BE=2m+6m=8m，2MC+2EC=2n+6n=8n，BC=BE+EC=3m+3n=3(m+n)，
∴2EF+2BE+2MC+2EC=8m+8n=8(m+n)，
设m+n=x，则长方形BEFG和长方形ECMN的周长之和为8x，BC=3x，
根据题意得8x=16，
解得x=2，
∴BC=3×2=6，
∴3CD=6，
解得CD=2，
∴BC⋅CD=6×2=12，
∴大灵动长方形ABCD的面积为12，
故答案为：12.
设EF=m，MC=n，则2EF+2BE+2MC+2EC=8m+8n=8(m+n)，设m+n=x，则长方形BEFG和长方形ECMN的周长之和为8x，BC=3x，于是列方程得8x=16，求得x=2，则BC=6，所以CD=2，即可求得大灵动长方形ABCD的面积为12，于是得到问题的答案．
此题重点考查一元一次方程的解法、列一元一次方程解应用题、新定义问题的求解等知识与方法，正解地求出大灵动长方形ABCD的边BC的长是解题的关键．
17.【答案】解：(1)3−(−2)+|−4|
=3+2+4
=9；
(2)−14× 25+32
=−1×5+9
=−5+9
=4.
【解析】(1)根据有理数的加减运算法则计算即可；
(2)根据有理数的乘方、算术平方根分别计算即可．
本题考查了实数的运算，熟练掌握实数的运算法则是解题的关键．
18.【答案】解：(1)8x−4=6x−8，
8x−6x=−8+4，
2x=−4，
x=−2；
(2)x+12−2=x−34，
2(x+1)−8=x−3，
2x+2−8=x−3，
2x−x=−3−2+8，
x=3.
【解析】(1)移项、合并同类项、系数化为1，依此即可求解；
(2)去分母、去括号、移项、合并同类项、系数化为1，依此即可求解．
考查了解一元一次方程，解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、系数化为1，这仅是解一元一次方程的一般步骤，针对方程的特点，灵活应用，各种步骤都是为使方程逐渐向x=a形式转化．
19.【答案】90∘(垂直的定义)∠DOF=90∘(已知)∠1=∠2(同角的余角相等)
【解析】解：∵OE⊥OA，
∴∠AOE=90∘(垂直的定义).
∴∠1+∠EOF=90∘.
∵∠DOF=90∘(已知)，
∴∠2+∠EOF=90∘，
∴∠1=∠2(同角的余角相等).
故答案为：90∘，垂直的定义；∠DOF=90∘，已知；∠1=∠2，同角的余角相等．
根据垂直的定义，以及同角的余角相等，进行作答即可．
本题考查垂直的定义，同角的余角，理清角度之间的关系，掌握垂直的定义，同角的余角相等是解题的关键．
20.【答案】解 原式=6a2b−2ab2−3a2b−3+6ab2+3
=3a2b+4ab2，
当a=3，b=−3时，
原式=3×32×(−3)+4×3×(−3)2
=3×9×(−3)+4×3×9
=−81+108
=27.
【解析】去括号，合并同类项，然后代入数值求解．
本题考查正式的加减，解题的关键是去括号，合并同类项，然后代入数值求解．
21.【答案】解：∵AB=6cm，AB=2BC，
∴BC=3cm，
∴AC=AB+BC=9cm，
∵D是线段AC的中点，
∴AD=12AC=4.5cm，
∴BD=AB−AD=1.5cm.
【解析】根据线段中点的意义，根据线段的和与差解决问题．
此题考查线段的和与差以及线段中点的意义，结合图形解题会变得形象直观．
22.【答案】解：设容器内的水将升高x cm，
根据题意得：6×8×2+4×4×(2+x)=6×8×(x+2)，
∴96+32+16x=48x+96，
解得x=1.
答：容器内的水将升高1cm.
【解析】设容器内的水将升高x cm，根据体积的计算方法列出方程，解之即可．
本题考查一元一次方程的实际应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．
23.【答案】解：(1)∵∠AOD=60∘，OC是∠AOD的平分线，
∴∠COD=12∠AOD=30∘，∠BOD=13∠AOD=20∘.
∴∠BOC=∠COD−∠BOD=30∘−20∘=10∘.
(2)由(1)得∠BOC=∠COD−∠BOD
=12∠AOD−13∠AOD
=16∠AOD
=n∘，
∴∠AOD=6∠BOC=6n∘.
【解析】(1)根据已知和角平分线的定义求得∠COD，∠BOD，再根据∠BOC=∠COD−∠BOD即可得到答案；
(2)由∠BOC=∠COD−∠BOD，根据角平分线的定义和已知，即可用含有n的代数式表示∠AOD.
本题考查了角平分线的定义，以及角的和差计算，掌握角平分线的定义是解题的关键．
24.【答案】解：(1)∵轨道长为91m，长度为1m的滑块从点A到点B的速度为9m/s，
∴第一阶段所用的时间为(91−1)÷9=10s，
∴当t=10s时，滑块右端刚好与点B重合，l1=9×10=90m，
答：当t=10s时，l1的值为90m；
(2)①∵整个过程用时27s，当滑块右端与点B重合时，滑块停顿2s，
∴第三阶段所用的时间为27−10−2=15s，
∴滑块返回的速度为(91−1)÷15=6m/s，
②分析可得：l1+l2+1=91，
当d=18m时，显然第二阶段时不满足，所以分两种情况：
1)当滑块从左向右滑动，即0≤t≤10时，l1=9t，l2=90−9t，d=l1−l2=18t−90.
18t−90=18，解得t=6；
2)当滑块从右向左滑动，即12≤t≤27时，l2=6(t−12)，l1=90−l2=162−6t，
d=l1−l2=162−6t−6(t−12)=−12t+234=18，
解得t=18.
综上所述，t的值为6或18.
【解析】(1)先求出第一阶段所用的时间，再根据速度，路程，时间的关系即可求出答案；
(2)①先求出第三阶段所用的时间，再根据速度，路程，时间的关系即可求出答案；
②分两种情况，即0≤t≤10时，12≤t≤27时，分别表示出l1，l2，再利用d=l1−l2列方程求出t的值即可．
本题考查一元一次方程的应用，解答中用的线段的和差关系，列代数式，理解题意，弄清数量关系是解题的关键．x
结果
代数式
2
n
3x+1
7
4
2x+1x
52
a