数学八年级下册6.4 三角形的中位线定理示范课课件ppt

这是一份数学八年级下册6.4 三角形的中位线定理示范课课件ppt，共20页。PPT课件主要包含了情境导入，学习目标，自学指导，中位线，Ｄ′D，你能验证你的猜想吗，三角形的中位线定理，符号语言，我来总结，正方形等内容，欢迎下载使用。
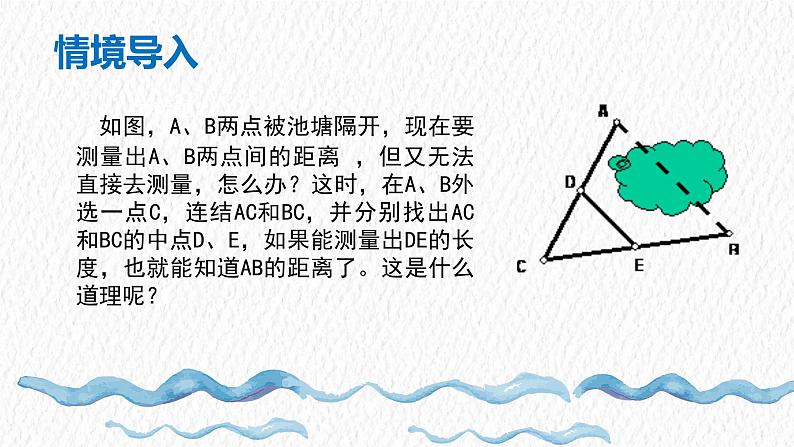
如图，A、B两点被池塘隔开，现在要测量出A、B两点间的距离 ，但又无法直接去测量，怎么办？这时，在A、B外选一点C，连结AC和BC，并分别找出AC和BC的中点D、E，如果能测量出DE的长度，也就能知道AB的距离了。这是什么道理呢？
1、理解三角形的中位线概念 2、探索并掌握三角形的中位线定理3、会利用三角形的中位线定理进行计算和证明
请同学们用5分钟时间自学课本30-32页实验探究（1）-（5），并思考下列问题
1.连接三角形两边 的 ，叫做三角形的中位线。
2.试画下面三角形的所有中位线：


3.通过上面作图，想一想：①一个三角形的中位线共有几条？ ②三角形的中位线与中线有什么区别？ ③你还有什么发现？
4.三角形中位线定理是什么？如何证明出来的？符号语言如何表达？

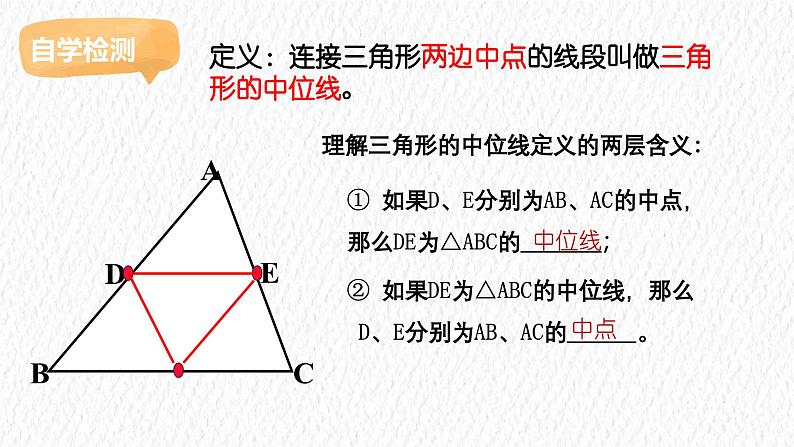
定义：连接三角形两边中点的线段叫做三角形的中位线。
理解三角形的中位线定义的两层含义:
① 如果D、E分别为AB、AC的中点，那么DE为△ABC的 ；
② 如果DE为△ABC的中位线，那么 D、E分别为AB、AC的 。
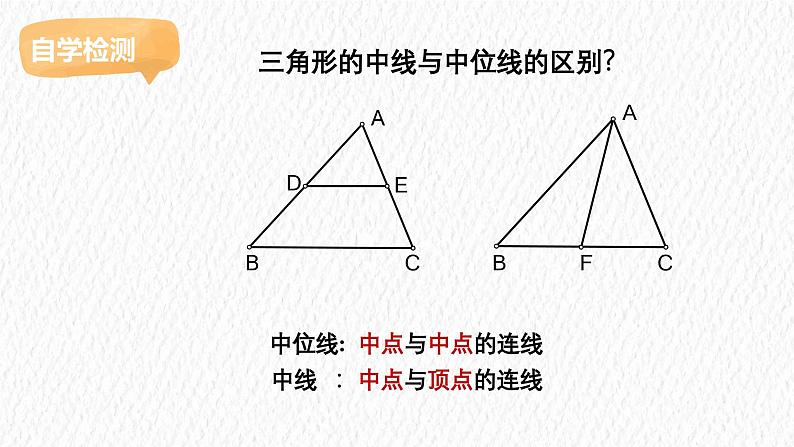
三角形的中线与中位线的区别？
中位线: 中点与中点的连线 中线 ：中点与顶点的连线
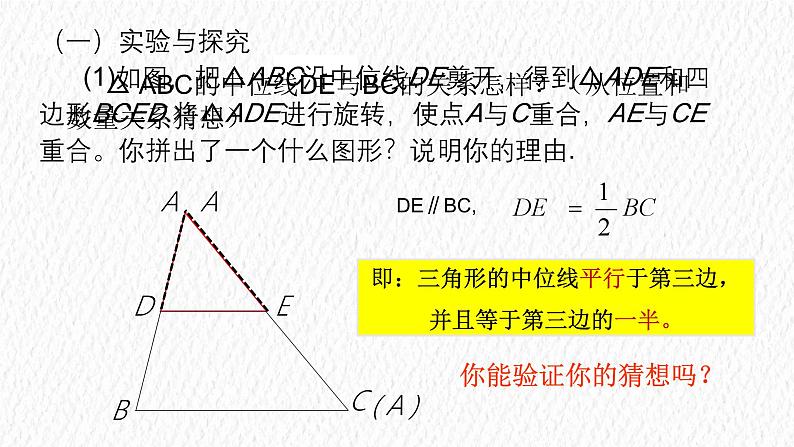
（一）实验与探究 (1)如图，把△ABC沿中位线DE剪开，得到△ADE和四边形BCED.将△ADE进行旋转，使点A与C重合，AE与CE重合。你拼出了一个什么图形？说明你的理由.
△ ABC的中位线DE与BC的关系怎样？（从位置和数量关系猜想）
即：三角形的中位线平行于第三边，并且等于第三边的一半。
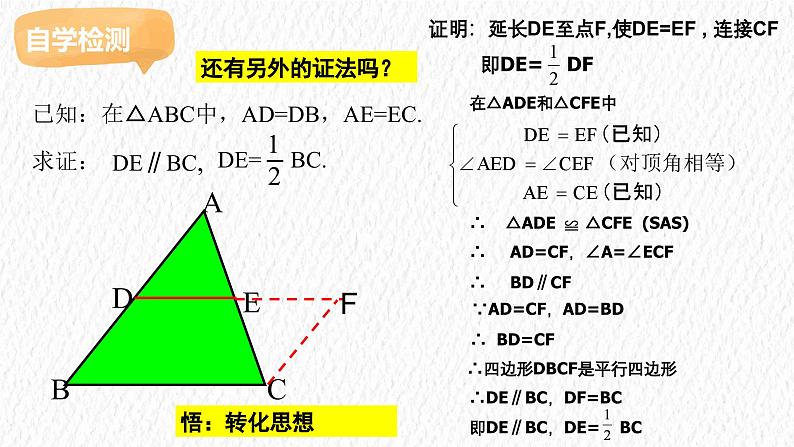
证明：延长DE至点F,使DE=EF , 连接CF 即DE= DF
在△ADE和△CFE中∴ △ADE △CFE (SAS) ∴ AD=CF，∠A=∠ECF∴ BD∥CF
∵AD=CF，AD=BD ∴ BD=CF ∴四边形DBCF是平行四边形
∴DE∥BC，DF=BC即DE∥BC，DE= BC
三角形的中位线平行于第三边，并且等于第三边的一半.
学习了中位线定理，本节课开始时提出的问题能否解决了呢？
练习1.如图，在△ABC中，D、E分别是AB、AC的中点
若∠ADE=65°，则∠B= 度，为什么？
若BC=8cm，则DE= cm，为什么？
若AC=4cm,BC=6cm，AB=8cm， 则△DEF的周长=______
练习1.如图，在△ABC中，D、E、F分别是AB、AC、BC的中点
若△ABC的周长为24，△DEF的周长是_____
1、 三角形三条中位线围成的三角形的周长与原三角形的周长的关系？
2、三角形三条中位线围成的三角形的面积与原三角形的面积的关系？
图中有_____个平行四边形
若△ABC的面积为24，△DEF的面积是_____
∵ E、F分别是AB、BC边的中点，∴EF是△ABC的中位线∴ EF//AC，EF= AC
∴EF//HG，EF=HG∴四边形EFGH是平行四边形
同理可得 HG//AC，HG= AC
（1）顺次连接对角线相等的四边形各边中点所得的四边形是什么？
（3）顺次连接对角线相等且垂直的四边形各边中点所得的四边形是什么？
（2）顺次连接对角线垂直的四边形各边中点所得的四边形是什么？
2．若顺次连接四边形四边中点所得的四边形是菱形，则原四边形（ 　） （A）一定是矩形 （B）一定是菱形 （C）对角线一定互相垂直　 （D）对角线一定相等
1.如图（1）ΔABC中， AB=6㎝， AC=8㎝，BC=10㎝，D﹑E﹑F分别是ABACBC的中点，则ΔDEF的周长是＿＿＿＿
3、如图，在△ABC中，AD是中线,EF是中位线.求证: AD与EF互相平分.
悟：三角形的一条中位线与第三边上的中线互相平分
4、 已知:如图所示,在四边形ABCD中,AD=BC,P为对角线BD的中点,M为DC的中点,N为AB的中点。求证：△PMN是等腰三角形。
证明:在△ABD中,∵N,P分别为AB,BD的中点, ∴PN= AD。同理PM= BC。
又∵AD=BC,∴PN=PM。 ∴△PMN是等腰三角形。
5.△ABC的中线BD，CE相交于O，F，G分别是BO，CO的中点，求证：四边形DEFG是平行四边形．
证明：连接DE，FG，
∵BD，CE是△ABC的中线，
∴D，E是AB，AC的中点.
∴DE∥FG，DE=FG.
∴四边形DEFG是平行四边形，
1.三角形中位线的定义
连接三角形两边中点的线段
2.三角形的中位线定理
三角形的中位线平行于第三边，并且等于第三边的一半
∵DE是△ABC的中位线∴ DE∥BC，
DE= BC.