初中人教版13.3.1 等腰三角形图片ppt课件

这是一份初中人教版13.3.1 等腰三角形图片ppt课件，共23页。PPT课件主要包含了教学目标，新课导入，情境引入，互动探究，等腰三角形的判定，建立数学模型，ABAC，你能验证你的结论吗，∠1∠2，∠B∠C等内容，欢迎下载使用。

1 .掌握等腰三角形的判定方法.（重点）2.掌握等腰三角形的判定定理，并运用其进行证明和计算.（难点）
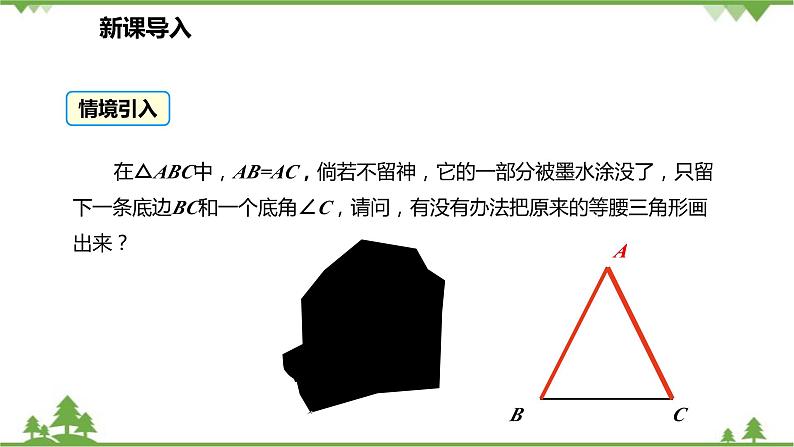
在△ABC中，AB=AC，倘若不留神，它的一部分被墨水涂没了，只留下一条底边BC和一个底角∠C，请问，有没有办法把原来的等腰三角形画出来？
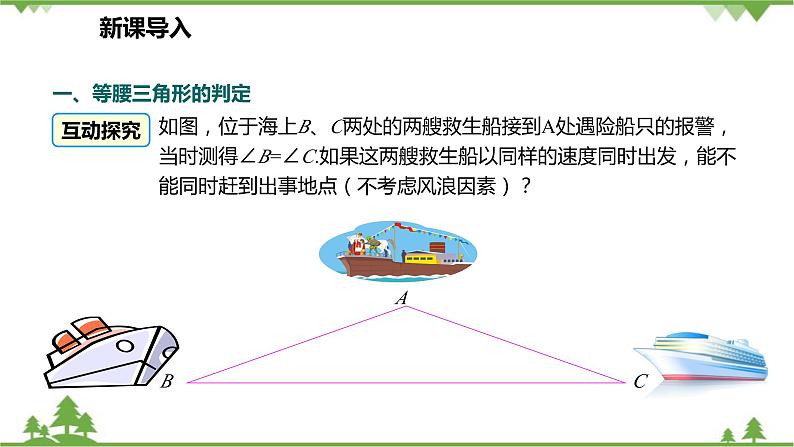
如图，位于海上B、C两处的两艘救生船接到A处遇险船只的报警，当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发，能不能同时赶到出事地点（不考虑风浪因素）？
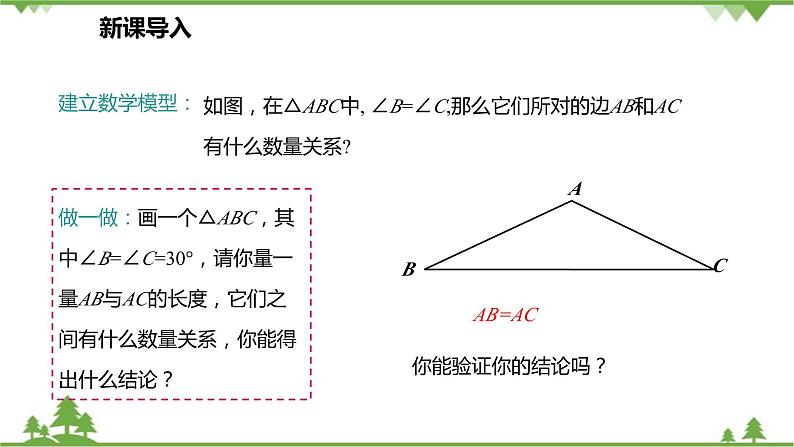
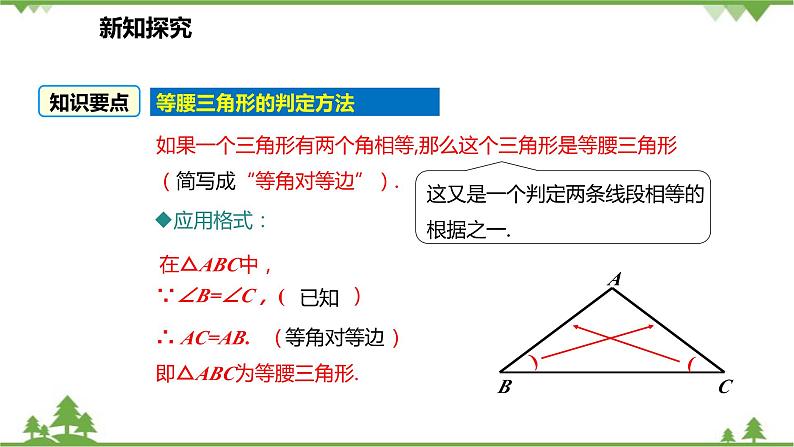
如图，在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系?
做一做：画一个△ABC，其中∠B=∠C=30°，请你量一量AB与AC的长度，它们之间有什么数量关系，你能得出什么结论？
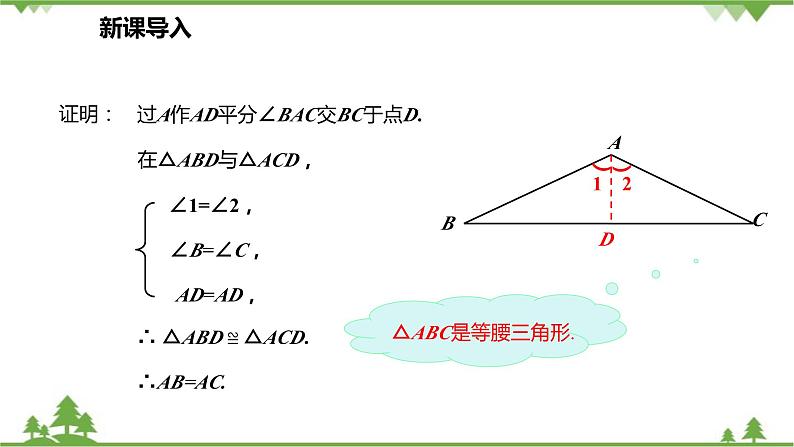
在△ABD与△ACD，
∴ △ABD ≌ △ACD.
过A作AD平分∠BAC交BC于点D.
∴ AC=AB. ( )即△ABC为等腰三角形.
∵∠B=∠C， ( )
如果一个三角形有两个角相等,那么这个三角形是等腰三角形（简写成“等角对等边”）.
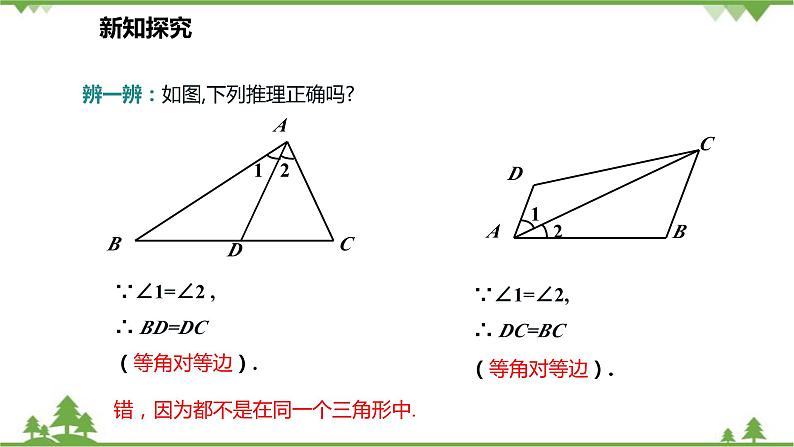
错，因为都不是在同一个三角形中.
辨一辨：如图,下列推理正确吗?
例1 求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．
已知： 如图，∠CAE是△ABC的外角，∠1=∠2，AD∥BC．
证明：∵AD∥BC， ∴∠1=∠B（两直线平行，同位角相等）， ∠2=∠C（两直线平行，内错角相等）． 又∵∠1=∠2， ∴∠B=∠C， ∴AB=AC（等角对等边）．
例2 已知：如图，AD∥BC，BD平分∠ABC. 求证：AB=AD
证明：∵ AD∥BC， ∴∠ADB=∠DBC. ∵ BD平分∠ABC， ∴∠ABD=∠DBC， ∴∠ABD=∠ADB， ∴AB=AD.
总结：平分角+平行=等腰三角形
如图，把一张长方形的纸沿着对角线折叠，重合部分是一个等腰三角形吗？为什么？
由折叠可知，∠EBD=∠CBD.
∵AD∥BC，∴∠EDB=∠CBD，
∴∠EDB=∠EBD，∴BE=DE，△EBD是等腰三角形.
练一练：1.在△ABC中，∠A和∠B的度数如下，能判定△ABC是等腰三角形 的是（ ） A. ∠A＝50°，∠B＝70° B. ∠A＝70°，∠B＝40° C. ∠A＝30°，∠B＝90° D. ∠A＝80°，∠B＝60°
2.如图，已知OC平分∠AOB，CD∥OB，若OD＝3cm，则CD等于_______.
例3 已知等腰三角形底边长为a,底边上的高的长为h，求作这个等腰三角形.
作法：1.作线段AB=a. 2.作线段AB的垂直平分线MN，交AB于点D. 3.在MN上取一点C，使DC=h. 4.连接AC，BC，则△ABC即为所求.
例4 如图，在△ABC中，∠ACB＝90°，CD是AB边上的高，AE是∠BAC的平分线，AE与CD交于点F，求证：△CEF是等腰三角形．
证明：∵在△ABC中，∠ACB＝90°， ∴∠B＋∠BAC＝90°. ∵CD是AB边上的高，∴∠ACD＋∠BAC＝90°， ∴∠B＝∠ACD. ∵AE是∠BAC的平分线，∴∠BAE＝∠EAC， ∴∠B＋∠BAE＝∠ACD＋∠EAC，即∠CEF＝∠CFE， ∴CE＝CF，∴△CEF是等腰三角形．
方法总结：“等角对等边”是判定等腰三角形的重要依据，是先有角相等再有边相等，只限于在同一个三角形中，若在两个不同的三角形中，此结论不一定成立．
例5 如图，在△ABC中，AB=AC，∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E，交AC于F. 探究EF、BE、FC之间的关系.
解：EF=BE+CF.理由如下：∵ EF∥BC,∴∠EOB=∠CBO，∠FOC=∠BCO. ∵ BO、CO分别平分∠ABC、∠ACB， ∴∠CBO＝∠ABO，∠BCO＝∠ACO，∴∠EOB＝∠ABO ，∠FOC＝∠ACO，∴BE＝OE，CF=OF，∴ EF=EO+FO＝BE+CF.
方法总结：判定线段之间的数量关系，一般做法是通过全等或利用“等角对等边”，运用转化思想，解决问题.
注意是指同一个三角形中
有两边相等的三角形是等腰三角形
1.如图，在△ABC中，AB＝AC，∠A＝36°，BD、CE分别是∠ABC、∠BCD的平分线，则图中的等腰三角形有( )A．5个 B．4个 C．3个 D．2个
2.一个三角形的一个外角为130°，且它恰好等于一个不相邻的内角的2倍.这个三角形是（ ）A．钝角三角形 　 B．直角三角形 　C．等腰三角形 　 D．等边三角形
3.如图，直线a、b相交于点O，∠1=50°，点A在直线a上，直线b上存在点B，使以点O、A、B为顶点的三角形是等腰三角形，这样的B点有（　　）A．1个 B．2个 C．3个 D．4个
解析：（1）以O 为圆心OA长为半径画弧，与直线b有两个交点；（2）以A为圆心OA长为半径画弧，与直线b有一个交点；（3）作线段OA的垂直平分线，与直线b有一个交点
4.如图，已知∠A=36°，∠ABD=36°，∠C=72°，则∠DBC=_____，∠BDC=_____，图中的等腰三角形有_______________________.
5.如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM＋CN＝9，则线段MN的长为_____.
6.如图,上午10 时，一条船从A处出发以20海里每小时的速度向正北航行，中午12时到达B处，从A、B望灯塔 C，测得∠NAC=40°，∠NBC=80°.求从B处到灯塔C的距离.
解：∵∠NBC=∠A+∠C， ∴∠C=80°- 40°= 40°， ∴ ∠C = ∠A， ∴ BA=BC（等角对等边）. ∵AB=20×（12-10）=40(海里), ∴BC=40海里. 答：B处距离灯塔C40海里.