广东省深圳外国语学校（集团）龙华高中部2021-2022学年高一上学期期中考试数学试卷+

这是一份广东省深圳外国语学校（集团）龙华高中部2021-2022学年高一上学期期中考试数学试卷+，文件包含深圳外国语学校集团龙华高中部2021-2022学年度第一学期数学参考答案期中考试docx、深圳外国语学校集团龙华高中部2021-2022学年度第一学期期中考试docx等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。

1．【答案】B
【详解】因为，，所以．
故选：B.
2．【答案】B
【详解】根据存在量词命题的否定为全称量词命题，
可得命题“，”的否定为“，”．
故选：B.
3．【答案】D
【详解】A：，因为，所以，所以，即，故A错误；
B：，因为，所以，所以，即，故B错误；
C：，因为，所以，
所以，即，故C错误；
D：因为，所以，故D正确.
故选：D.
4．【答案】C
【详解】由题意，图中的阴影部分是的子集，但不属于集合，属于集合的补集，
即是集合的子集，所以阴影部分表示的集合为.
故选：C.
5．【答案】A
【详解】,当且仅当，即时，等号成立，所以的最小值等于.
故选：A.
6．【答案】C
【详解】第一次操作剩下的区间为、；
第二次操作剩下的区间为、、、；
第三次操作剩下的区间为、、、、、、、．
即从左到右第四个区间为．
故选：C.
7．【答案】D
【详解】∵是偶函数，且在上的单调递减，则在单调递增，
又，则，解得.
故选：D.
8．【答案】C
【详解】由高斯函数的定义可得：
当时，，则，
当时，，则，
当时，，则，
当时，，则，
当时，，则，
当时，，则，
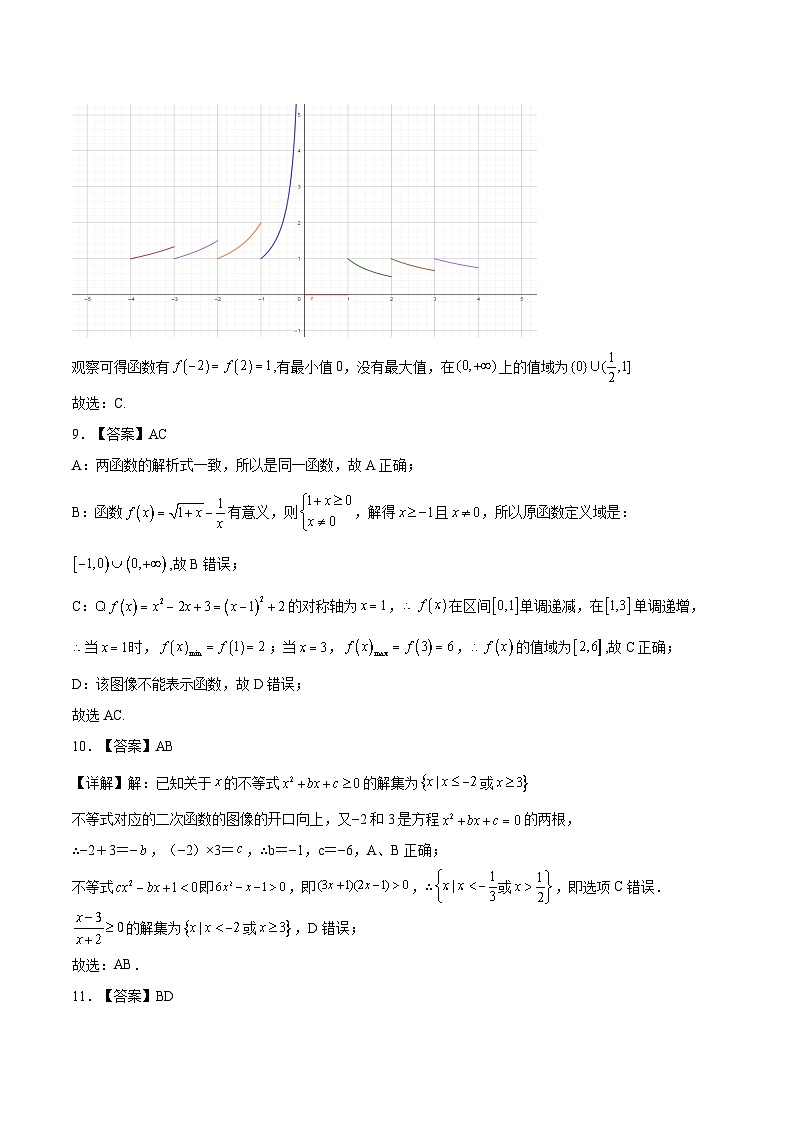
绘制函数图象如图所示，
观察可得函数有,有最小值0，没有最大值，在上的值域为
故选：C.
9．【答案】AC
A：两函数的解析式一致，所以是同一函数，故A正确；
B：函数有意义，则，解得且，所以原函数定义域是：,故B错误；
C：的对称轴为，在区间单调递减，在单调递增，
当时，；当，，的值域为,故C正确；
D：该图像不能表示函数，故D错误；
故选AC.
10．【答案】AB
【详解】解：已知关于的不等式的解集为或
不等式对应的二次函数的图像的开口向上，又−2和3是方程的两根，
∴−2＋3＝−，（−2）×3＝，∴b＝−1，c＝−6，A、B正确；
不等式即，即，∴或，即选项C错误．
的解集为或，D错误；
故选：AB．
11．【答案】BD
【详解】根据题意和图（2）知，两直线平行即票价不变，
直线向上平移说明当乘客量为时，收入是但支出变少，即说明此建议是减少支出而保持票价不变；
由图（3）看出，当乘客量为时，支出不变，但是直线的倾斜角变大，即相同的乘客量时收入变大，
即票价提高了，即说明了此建议是提高票价而保持成本不变．
故选：BD．
12．【答案】ABD
【详解】方程，则或，
所以当时，或，
当时，或，
当时，，
因为正整数解集只有三个元素，所以且，故A、B正确，C错误；
当时，
当时，，故D正确
故选：ABD
13．【答案】8
【详解】由集合，，即是的子集
满足条件的集合的个数为.
故答案为.
14．【答案】必要不充分
【详解】等价于，故推不出，由能推出．
故“”是“”的必要不充分条件．
故答案为：必要不充分．
15．【答案】
【详解】若，在区间单调递减，不符合题意；
若，因为二次函数在区间上单调递增，
所以 ,解得．
故答案为：.
16．【答案】 .
【详解】（1）根据题意，，即，
则，则；
（2）根据题意，分2种情况讨论：
①当时，，则有，此时，
若，即，
解可得：，此时的取值范围为，；
②当时，，则有，
其中当时，，此时，
若，即，解可得：，舍去
当时，，此时，若，即，解可得：，
此时的取值为，；
综合可得：的取值范围为,.
17．【答案】（1）；（2）答案见解析.
【详解】（1）因为即，所以…………………………2
.…………………………4
（2）若选择①，即是的充要条件，则，…………………………6
即解得,…………………………8
故实数．…………………………9
若选择②，即是的充分不必要条件，则
则且（两个等号不同时成立），
解得，故实数m的取值范围是．
若选择③，即是的必要不充分条件，则
当时，，解得．
当时，且（两个等号不同时成立），
解得，故实数m的取值范围是．
18．【答案】（1）；（2）证明见解析，最大值，最小值
【详解】（1）解：， …………………………1
解得，…………………………2
所以；…………………………3
（2）函数是区间上的减函数.
证明：，，且，…………………………4
则，……………………5
因为，所以，，
于是，即，…………………………6
所以函数是区间上的减函数.…………………………7
所以当时，取最大值；…………………………8
当时，取最小值.…………………………9
19．【答案】（1）;(2)当时，总造价最低，最低总造价为元.
【详解】（1）因为游泳池的长为，所以游泳池的宽为，…………………………1
铺游泳池的花费为，…………………………3
休闲区的花费为，…………………………5
所以，总造价为.…………6
（2）由基本不等式可得
（元），………………………8
当且仅当时，等号成立.…………………………9
因此，当时，总造价最低，且最低总造价为元.…………………………10
20．【答案】（1）8；（2）．
【详解】（1）…………………………1
，…………………………3
当且仅当时等号成立，因为，
，，解得，时等号成立，…………………………4
此时的最小值是8．…………………………5
（2）因为，在上恒成立，………………………6
∴…………………………8
解得：.…………………………10
21．【答案】（1）；（2）
【详解】解:(1)设，则，…………………………1
因为是定义在上的奇函数，且当时，，
所以，…………………………3
所以 …………………………4
画出的函数图像：
…………………………5
（2）由（1）有
①当时，在上单调递增,故…………………………6
②当时，在上单调递增,在上单调递减，故…………………………7
③当时，在和上单调递增,在上单调递减，但
故…………………………8
④当时，在和上单调递增,在上单调递减，此时
故…………………………9
综上：.…………………………10
22．【答案】(1)开放答案，答案不唯一;(2)不是精彩函数,证明见解析;(3).
【详解】(1)由精彩函数的定义，，，，均为符合条件的精彩函数.…………………………2
(2)不是精彩函数，理由如下：
易知函数在区间上单调递增,…………………………3
若为精彩函数，即存在区间为精彩区间，则有，…………………………4
得，这显然不成立
所以函数不是精彩函数.…………………………5
(3)由函数定义域为,且易知函数在定义域上为单调递增函数,……………………6
因函数是精彩函数,则需有两个不等的实数解,即方程有两个不等的实数根.…………………………7
设为,且,, ,
则令,
由题意得:…………………………9
联立解得.…………………………10