北师大版数学七年级下册 4.3 第1课时 利用“边边边”判定三角形全等课件

这是一份北师大版数学七年级下册 4.3 第1课时 利用“边边边”判定三角形全等课件，共28页。

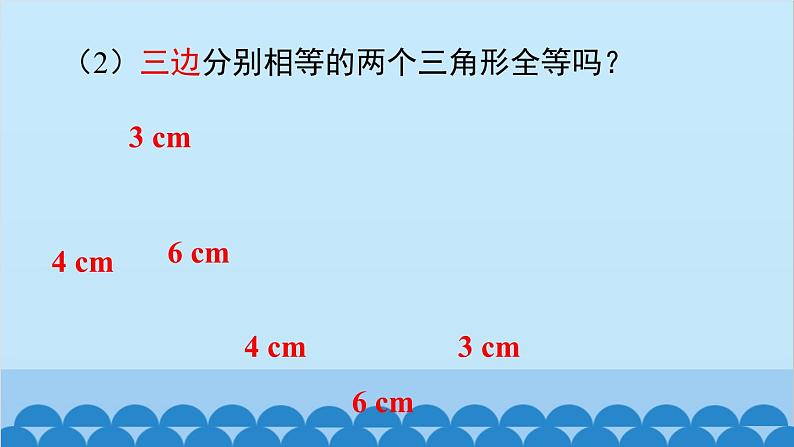
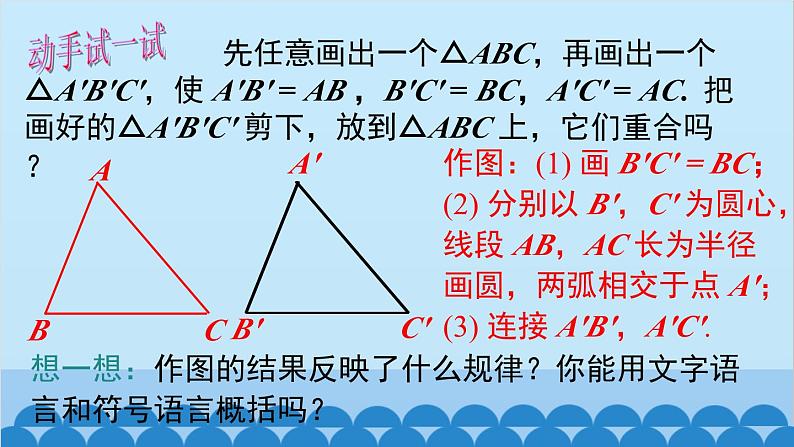
3 探索三角形全等的条件第四章 三角形第1课时 利用“边边边”判定三角形全等1. 什么叫全等三角形？能够完全重合的两个三角形叫全等三角形.3. 已知△ABC≌△DEF，找出其中相等的边与角.① AB = DE③ CA = FD② BC = EF④∠A =∠D⑤∠B =∠E⑥∠C =∠F2. 全等三角形有什么性质？全等三角形的对应边相等，对应角相等. 如果只满足这些条件中的一部分，那么能保证△ABC≌△DEF 吗?想一想：即：三条边分别相等，三个角分别相等的两个三角形全等．探究活动1：一个条件可以吗？（1）有一条边相等的两个三角形不一定全等（2）有一个角相等的两个三角形不一定全等结论：有一个相等条件不能保证两个三角形全等.三角形全等的判定（“边边边”）有两个分别相等的条件不能保证三角形全等.不一定全等探究活动2：两个条件可以吗？不一定全等不一定全等结论：(1) 有两个角分别相等的两个三角形(2) 有两条边分别相等的两个三角形(3) 有一个角和一条边分别相等的两个三角形结论：三个内角分别相等的三角形不一定全等.（1）有三个角分别相等的两个三角形探究活动3：三个条件可以吗？（2）三边分别相等的两个三角形全等吗？ 先任意画出一个△ABC，再画出一个△A′B′C′，使 A′B′ = AB ，B′C′ = BC，A′C′ = AC. 把画好的△A′B′C′ 剪下，放到△ABC 上，它们重合吗？A′B′C′想一想：作图的结果反映了什么规律？你能用文字语言和符号语言概括吗？作图：(1) 画 B′C′ = BC；(2) 分别以 B'，C' 为圆心，线段 AB，AC 长为半径画圆，两弧相交于点 A'；(3) 连接 A'B'，A'C'.动手试一试文字语言：三边分别相等的两个三角形全等， 简写为“边边边”或“SSS”.“边边边”判定方法几何语言：在△ABC 和△DEF 中，所以△ABC≌△DEF（SSS）.例1 如图，有一个三角形钢架，AB = AC，AD 是连接点 A 与 BC 中点 D 的支架.试说明：(1)△ABD≌△ACD；解题思路：先找隐含条件公共边 AD再找现有条件AB = AC最后找准备条件BD = CDD 是 BC 的中点解：因为 D 是 BC 中点， 所以 BD = DC． 在△ABD 与△ACD 中，所以△ABD≌△ACD (SSS).准备条件指明范围摆齐根据写出结论(2)∠BAD =∠CAD.解：由（1）得△ABD≌△ACD，所以 ∠BAD = ∠CAD（全等三角形对应角相等）.如图，C 是 BF 的中点，AB = DC，AC = DF.试说明：△ABC≌△DCF.在△ABC 和△DCF 中，AB = DC所以△ABC≌△DCF(已知)，(已证)，AC = DFBC = CF解：因为 C 是 BF 中点，所以 BC = CF.(已知)，(SSS).针对训练已知：如图，点 B、E、C、F 在同一直线上，AB = DE， AC = DF，BE = CF.试说明：（1）△ABC≌△DEF； （2）∠A =∠D.解：所以 △ABC≌△DEF (SSS).在△ABC 和△DEF 中，因为 AB = DE，AC = DF，BC = EF，因为 BE = CF，所以 BC = EF.所以 BE + EC = CF + CE.（1）（2）因为△ABC≌△DEF（已证），所以∠A =∠D（全等三角形对应角相等）.变式题典例精析 例2 “三月三，放风筝”．下图是小明制作的风筝，他根据 DE＝DF，EH＝FH，不用度量，就知道∠DEH＝∠DFH．请你用所学的知识说明理由．所以 △DEH≌△DFH (SSS).解：在△DEH 和△DFH 中，因为 DE = DF，EH = FH，DH = DH，所以∠DEH =∠DFH.动手做一做1. 将三根木条用钉子钉成一个三角形木架.2. 将四根木条用钉子钉成一个四边形木架.点击视频开始播放↑三角形的稳定性请同学们看看三角形和四边形的模型，扭一扭模型，它们的形状会改变吗?动动手不会会1. 三角形具有稳定性.2. 四边形没有稳定性.发现理解“稳定性” “只要三角形三条边的长度确定了，这个三角形的形状和大小也就完全确定了”，三角形的这个性质叫做“三角形的稳定性”. 这就是说，三角形的稳定性不是“拉得动、拉不动”的问题，其实质应是“三角形的三边长一旦确定，其形状和大小就唯一确定了”.比一比，谁知道的多 你能举出一些现实生活中应用三角形的稳定性的例子吗?△ABC ≌ (SSS). （1）如图，AB = CD，AC = BD，△ABC 和△DCB 是否全等？试说明理由. 解： △ABC≌△DCB.理由如下： AB = DC， AC = DB， = ，（2）如图，D、F 是线段 BC 上的两点，AB=CE，AF=DE，要使△ABF≌△ECD，还需要条件 . BCCB△DCBBF = CD1. 填空题：或 BD = FC2. 如图，桥梁的斜拉钢索是三角形的结构，主要是为了 ( ) A. 节省材料，节约成本 B. 保持对称 C. 利用三角形的稳定性 D. 美观漂亮C3. 如图，AB = AC，DB = DC，请说明∠B =∠C 成立的理由.ABCD在△ABD 和△ACD 中，AB = AC (已知)，DB = DC (已知)， AD = AD (公共边)，所以△ABD≌△ACD (SSS).解：连接 AD.所以∠B =∠C (全等三角形的对应角相等).4. 已知 AC = AD，BC = BD，试说明：AB 是∠DAC 的平分线.AC = AD ( )，BC = BD ( )，AB = AB ( )，所以△ABC≌△ABD ( ).所以∠1 =∠2所以 AB 是∠DAC 的平分线(全等三角形的对应角相等).已知已知公共边SSS(角平分线的定义).解：在△ABC 和△ABD 中，三边分别相等的两个三角形三角形全等的“SSS”判定：三边分别相等的两个三角形全等.三角形的稳定性：三角形三边长度确定了，这个三角形的形状和大小就完全确定了.欢迎各位老师对此课件提出宝贵的建议，我们将更好的为您服务。扫描二维码，添加我的企业微信吧~如果您有兴趣参与课件编写，请扫码添加优翼教育产品顾问李老师微信~感谢您使用我们的课件！李潇潇