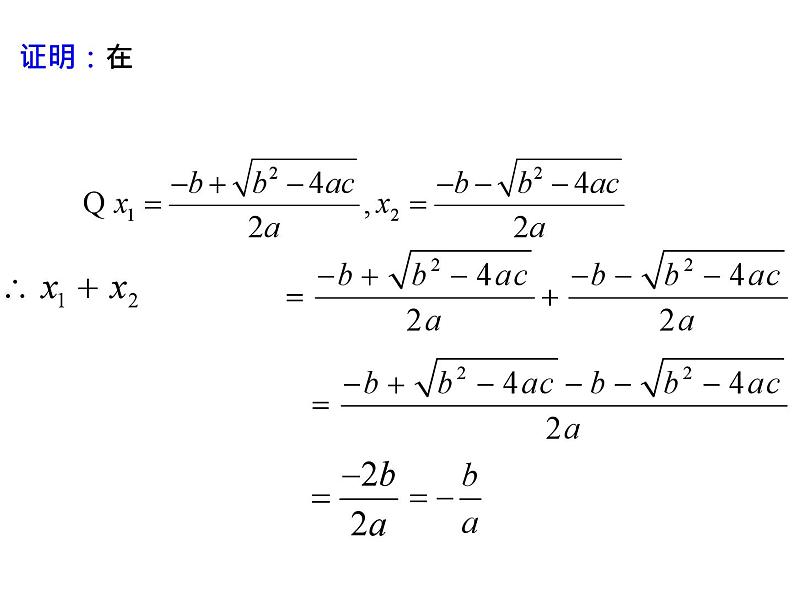
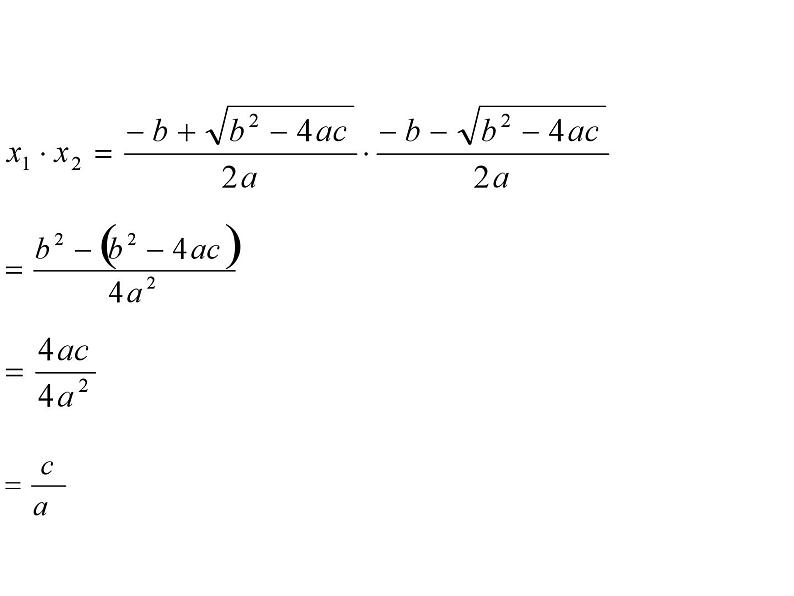
浙教版八年级下册2.4 一元二次方程根与系数的关系（选学）教学ppt课件

这是一份浙教版八年级下册2.4 一元二次方程根与系数的关系（选学）教学ppt课件，共24页。PPT课件主要包含了课前回顾，情境导入，证明在，练习1，x1+x22，x1x2-1，x1+x23，x1x20，练习2，课本例题等内容，欢迎下载使用。
1.一元二次方程的一般形式是什么？
2.一元二次方程根的判别式是什么？
3.一元二次方程的求根公式是什么？
4.一元二次方程的根的情况怎样确定？
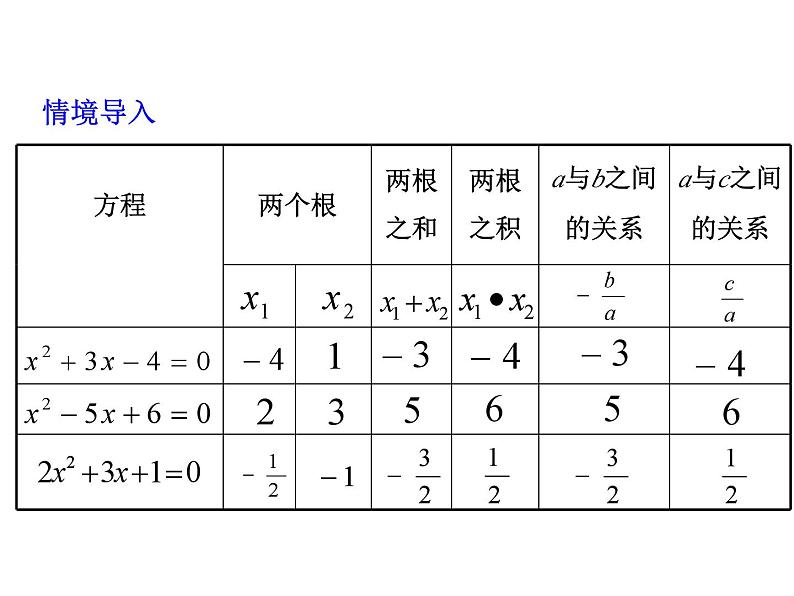
如果一元二次方程 的两个根分别是 ， ，那么你可以发现什么结论？
这种关系是这几个方程所特有的还是对于任意的一元二次方程都适合的呢？我们来证明一下
如果一元二次方程 的两个根分别是 ， ，那么：
能用这个结论的前提为△≥0
利用根与系数的关系求方程的两根的和与积
1.说出下列各方程的两根之和与两根之积：
(1) x2 - 2x - 1=0
(2) 2x2 - 6x =0
求：(1) ; (2) .
分析：求与方程的根有关的代数式的值时，一般先将所求的代数式化成含两根之和或两根之积的形式，再整体代入．
例2：已知一个一元二次方程的二次项系数是3，它的两个根分别是 请写出这个方程。
解：设这个方程为 ，由一元二次方程根与系数的关系，得
1.若关于x的一元二次方程的两根互为相反数，求m的值.
解：∵x1，x2是方程2x2-3x+m=0的两个实数根， ∴x1+x2=   ①. 而8x1-2x2=7 ②， 联立①②，解得x1=1，x2= ， ∴x1•x2= = ， ∴m=1．
1.已知方程 的两根之和与两根之积相等，那么m的值为（ ） A.1 B.-1 C. 2 D. -22.已知方程 的两根之和为4，积为-3，则a= ，b= 。
3.设x1，x2是方程2x2－9x＋6＝0的两个根，求下列各式的值：
分析：利用根与系数的关系求有关代数式的值的一般方法：(1)利用根与系数的关系求x1＋x2，x1x2的值；(2)将所求的代数式变形转化为用含x1＋x2，x1x2的代数式表示；(3)将x1＋x2，x1x2的值整体代入求出待求式的值．
已知方程x2-(k+1)x+3k=0的一个根是2 ,求它的另一个根及k的值.（用两种方法解答）
设方程的另一个根为x2.
2 ＋ x2 = k+1
答：方程的另一个根是-3 , k的值是-2.
已知方程x2-(k+1)x+3k=0的一个根是2 ,求它的另一个根及k的值。（用两种方法解答）
把x=2代入方程，得4-2(k+1)+3k=0
解这个方程，得 k= -2
由根与系数的关系，得2x2＝3k
答：方程的另一个根是-3,k的值是-2.