17.2《一次函数的图象》华师版数学八年级下册优质教学课件

这是一份17.2《一次函数的图象》华师版数学八年级下册优质教学课件，共18页。

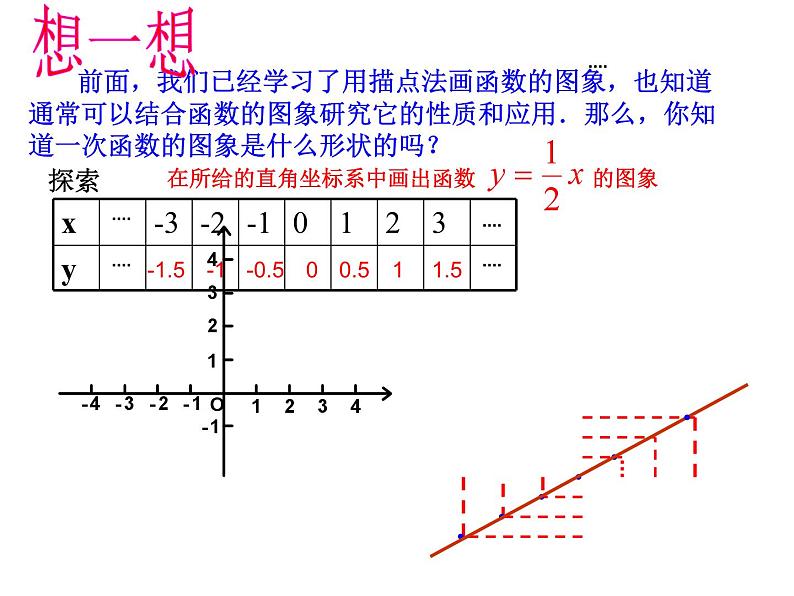
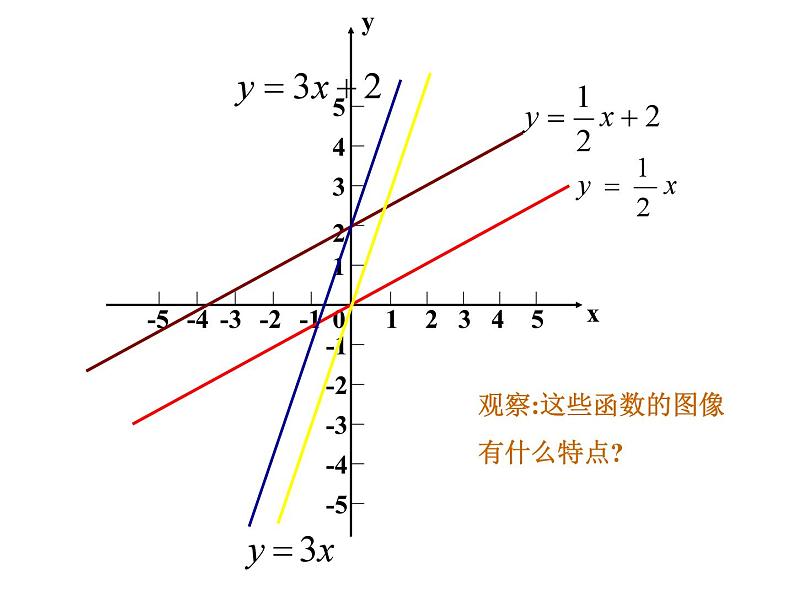
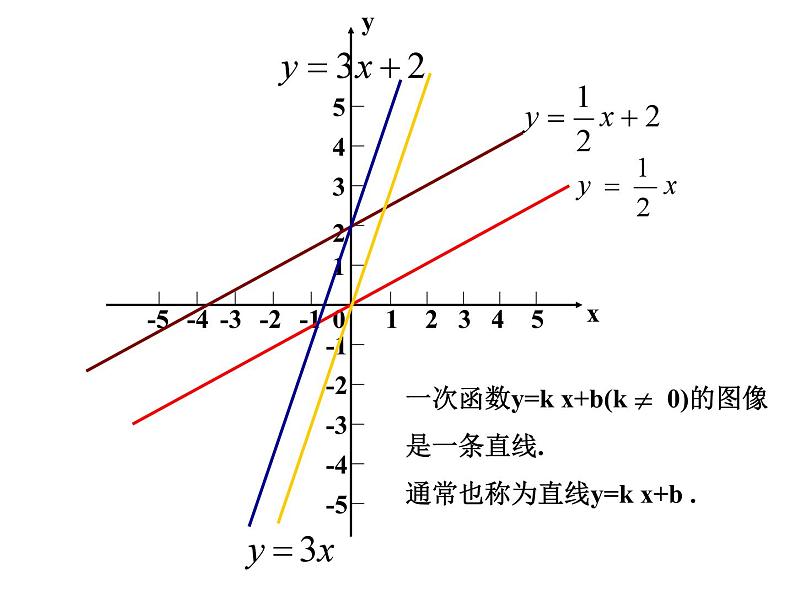
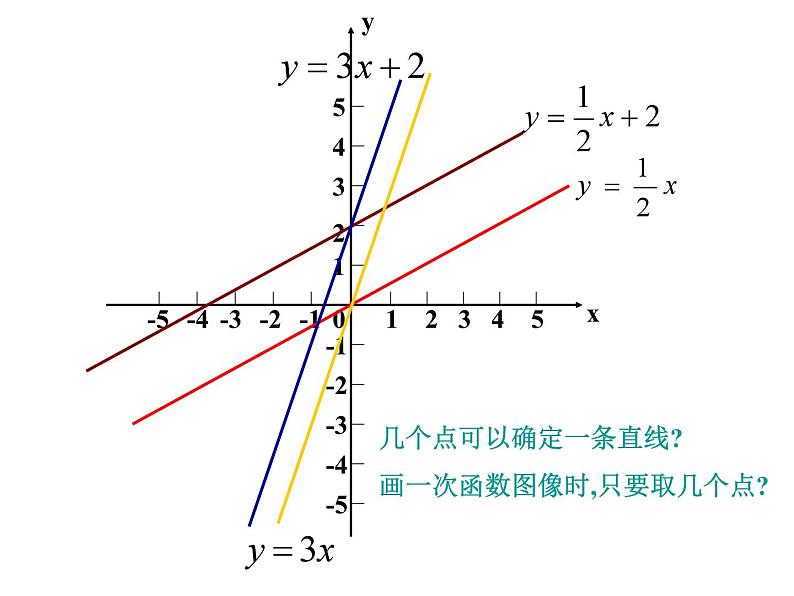
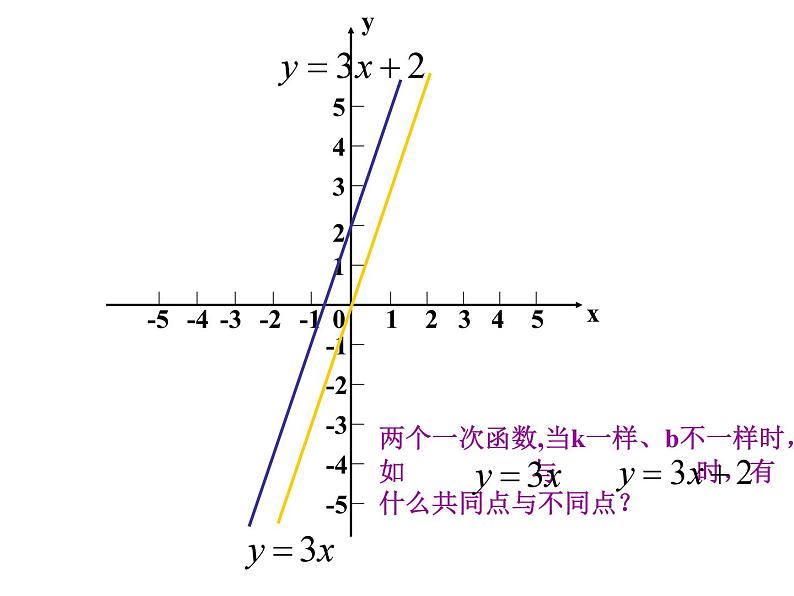
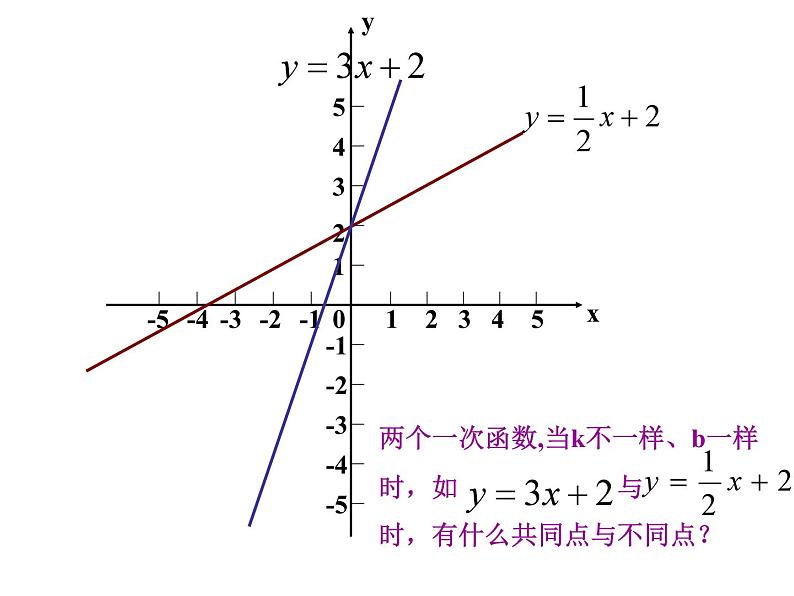
一次函数的图象 前面，我们已经学习了用描点法画函数的图象，也知道通常可以结合函数的图象研究它的性质和应用．那么，你知道一次函数的图象是什么形状的吗？ 想一想在所给的直角坐标系中画出函数 的图象探索 -1.5-1-0.500.511.5●●●●●●(1) (2) (3) (4) 请同学们根据画图象的步骤：列表、描点、连线，在同一平面直角坐标系中画出下列函数的图象: 观察：它们有什么特点？1-12345-4-3-2-512345-1-2-3-4-50观察:这些函数的图像有什么特点?xy1-12345-4-3-2-512345-1-2-3-4-50yx1-12345-4-3-2-512345-1-2-3-4-50几个点可以确定一条直线? 画一次函数图像时,只要取几个点?yx1-12345-4-3-2-512345-1-2-3-4-50两个一次函数,当k一样、b不一样时，如 与 时，有什么共同点与不同点？yx1-12345-4-3-2-512345-1-2-3-4-50两个一次函数,当k不一样、b一样时，如 与 时，有什么共同点与不同点？yx 答：两个点，因为一次函数的图象是一条直线，而且取两个点简便解：（1）列表解：（2）列表(1)(2)两题中每组中的两条直线有什么关系？复习与回顾1.一次函数的图象是什么形状？画一次函数的图象只要确定几个点？一次函数的图象是一条直线.通常也叫做直线y=kx+b2.对于几个一次函数(直线) y = kx + b (k≠0)当k相等b不相等时,这些直线的位置关系是怎样的?当b相等k不相等时,这些直线又有什么相同之处?1-12345-4-3-2-512345-1-2-3-4-50yx●求直线 y=-2x-3与x轴和y轴的交点,并画出这条直线.x 0 -1.5y -3 0••y=-2x-3解： 画出一次函数图象的关键是选取适当的两点，然后连线即可。为了描点方便，对于一次函数y=kx+b(k,b是常数,k≠0)通常选取(0,b)与( － b /k ,0 )两点。 小明暑假第一次去北京．汽车驶上A地的高速公路后，小明观察里程碑，发现汽车的平均速度是95千米/时．已知A地直达北京的高速公路全程570千米，小明想知道汽车从A地驶出后，距北京的路程和汽车在高速公路上行驶的时间有什么关系，以便根据时间估计自己和北京的距离． 设汽车在高速公路上行驶时间为t小时，汽车距北京的路程为s千米，则s与t的函数关系式为 ___________________________________________________________________s＝570－95t例3: 画出上述问题中小明距北京的路程 s 与开车时间t 之间函数s＝570－95t的图象． 这里s和t取的值悬殊较大，怎么办？分析：　在实际问题中，我们可以在表示时间的 t 轴和表示路程的s轴上分别选取适当的单位长度，画出平面直角坐标系并画出这个函数的图象（如图）： 讨 论： 1. 这个函数是不是一次函数？2. 这个函数中自变量t的取值范围是什么？函数的图象是什么？ 3. 在实际问题中，一次函数的图象除了直线和本题的图形外，还有没有其他情形？你能不能找出几个例子加以说明？ 　 1、某企业去年积压产品a件(a>0)，今年预计每月销售产品2b件，同时每月可生产出产品b个，若产品积压量y(件)是今年开工时间（月）的函数，则它的图象只能是（ ）函数解析式为：y = a-bxC练习: 　 2、 如图，l1反映了某公司产品的销售收入与销售量的关系，l2反映了该公司产品的销售成本与销售量的关系，根据图意填空：（1）当销售量为2吨时，销售收入＝　　　　元，　　　销售成本＝　　　　元；20003000 　 （2）当销售量为6吨时，销售收入＝　　　　元，　　　销售成本＝　　　　元；60005000（3）当销售量为　　时，销售收入等于销售成本；4吨 　 （4）当销售量　　　　时，该公司赢利（收入大于成本）；当销售量　　　　时，该公司亏损（收入小于成本）；大于4吨小于4吨