专题8.9 空间角与空间距离大题专项训练-2023-2024学年高一数学下学期高效讲练测（人教A版必修第二册）

这是一份专题8.9 空间角与空间距离大题专项训练-2023-2024学年高一数学下学期高效讲练测（人教A版必修第二册），文件包含专题89空间角与空间距离大题专项训练举一反三人教A版必修第二册原卷版docx、专题89空间角与空间距离大题专项训练举一反三人教A版必修第二册解析版docx等2份试卷配套教学资源，其中试卷共69页， 欢迎下载使用。
姓名：___________班级：___________考号：___________
题型一
异面直线所成的角
1．（2023·湖南岳阳·校联考模拟预测）如图，已知长方体ABCD−A1B1C1D1的底面ABCD是边长为2的正方形，O为其上底面A1B1C1D1的中心，在此长方体内挖去四棱锥O−ABCD后所得的几何体的体积为823.
(1)求线段AA1的长；
(2)求异面直线AO与C1D1所成的角.
【解题思路】（1）根据棱柱和棱锥的体积公式计算即可；
（2）取A1D1的中点E，连接AE,OE，则OE// C1D1，则∠AOE是两异面直线AO与C1D1所成的角，再解Rt△AOE即可.
【解答过程】（1）依题意，得2×2×AA1−13×2×2×AA1=823，
解得AA1=2；
（2）如图，取A1D1的中点E，连接AE,OE，则OE// C1D1，
所以∠AOE是两异面直线AO与C1D1所成的角，
因为OE// C1D1,C1D1⊥平面ADD1A1，所以OE⊥平面ADD1A1，
又AE⊂平面ADD1A1，所以OE⊥AE，
在Rt△AOE中，OE=1,AE=AA12+A1E2=3，
则tan∠AOE=AEOE=3，所以∠AOE=60∘，
所以异面直线AO与C1D1所成的角为60∘.
2．（2023上·江苏·高一校联考阶段练习）如图所示，正四棱锥P−ABCD中，O为底面正方形的中心，侧棱PA与底面ABCD所成的角的正切值为62.

(1)若E是PB的中点，求异面直线PD与AE所成角的正切值；
(2)在（1）的条件下，问在棱AD上是否存在一点F，使EF⊥侧面PBC，若存在，试确定点F的位置；若不存在，说明理由.
【解题思路】（1）取AD中点M，连接OM、PM，由正四棱锥的性质知∠PMO为所求二面角P−AD−O的平面角，∠PAO为侧棱PA与底面ABCD所成的角，设AB=a，求出tan∠PMO的值，即可得解；
（2）延长MO交BC于N，取PN的中点G，连接EG、MG，易得BC⊥平面PMN，可得平面PMN⊥平面PBC，分析出△PMN为正三角形，易证MG⊥平面PBC，取AM的中点F，连接EF，可得四边形EFMG为平行四边形，从而MG//FE，可得EF⊥平面PBC，即可得出结论.
【解答过程】（1）
连接AE、OE，
所以，∠AEO为异面直线PD与AE所成的角.
∵PO⊥平面ABCD，AO⊂平面ABCD，则AO⊥PO，
∵AO⊥BD，BD∩PO=O，∴AO⊥平面PBD，
又OE⊂平面PBD，∴AO⊥OE.
侧棱PA与底面ABCD所成的角的正切值为62，即tan∠PAO=POAO=62，
设底面边长为a，则AO=22a，所以PO=32a，
∵OE=12PD=12PO2+DO2=54a，所以，tan∠AEO=AOEO=2105.
（2）
延长MO交BC于N，则N为BC的中点，取PN的中点G，连接EG、MG.
因为PB=PC，N为BC的中点，则BC⊥PN，同理可得BC⊥PM，
∵PM∩PN=P，故BC⊥平面PMN，
∵BC⊂平面PBC，∴平面PMN⊥平面PBC，
又PM=PA2−AM2=PB2−BN2=PN，∠PMN=60°，
所以，△PMN为正三角形，∵G为PN的中点，则MG⊥PN，
又因为平面PMN∩平面PBC=PN，平面PMN⊥平面PBC，MG⊂平面PMN，
所以，MG⊥平面PBC，
取AM的中点F，连接EF，

∵G、E分别为PN、PB的中点，则EG//BN且EG=12BN，
因为AD//BC且AD=BC，M、N分别为AD、BC的中点，则AM//BN且AM=BN，
∵F为AM的中点，则FM//BN且FM=12BN，故FM//EG且FM=EG，
所以，四边形EFMG为平行四边形，则EF//MG，故EF⊥平面PBC.
因此，F是AD的4等分点，靠近A点的位置.
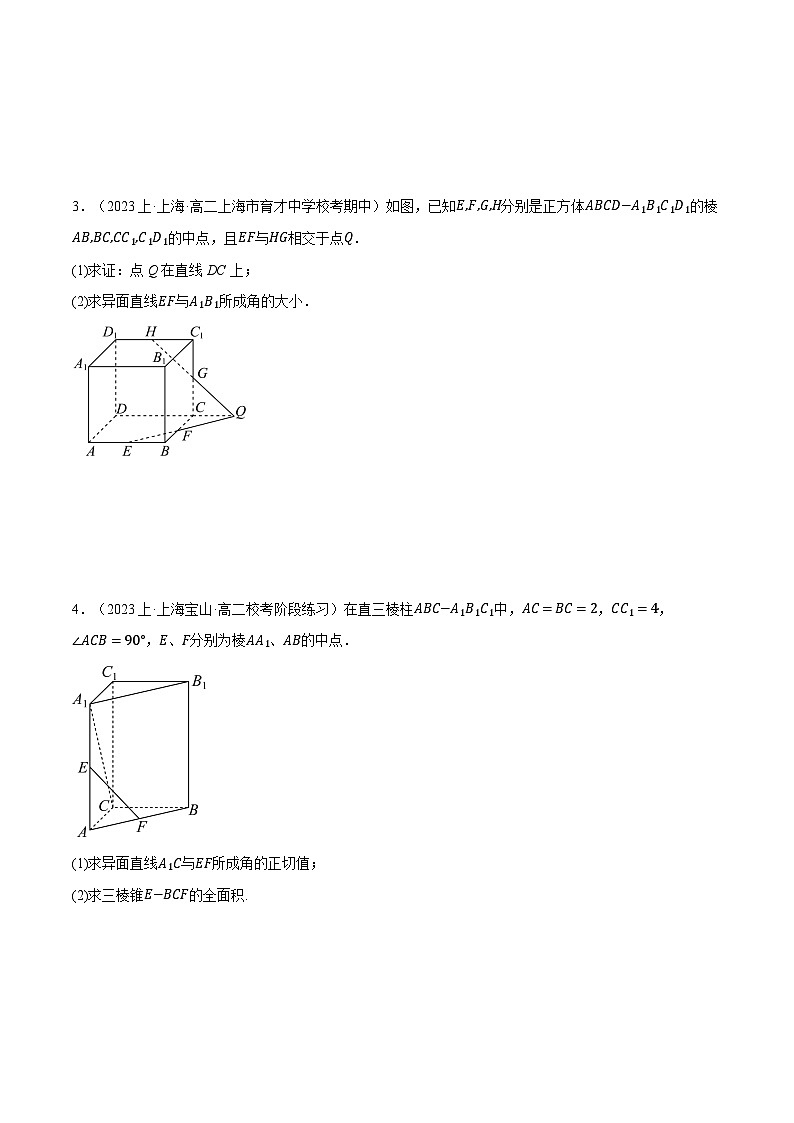
3．（2023上·上海·高二上海市育才中学校考期中）如图，已知E,F,G,H分别是正方体ABCD−A1B1C1D1的棱AB,BC,CC1,C1D1的中点，且EF与HG相交于点Q．
(1)求证：点Q在直线DC上；
(2)求异面直线EF与A1B1所成角的大小．
【解题思路】（1）通过证明Q在平面ABCD与平面CDD1C1的交线上，来证得Q在直线DC上.
（2）判断出异面直线EF与A1B1所成角并计算出角的大小.
【解答过程】（1）平面ABCD∩平面CDD1C1=DC，
由于Q∈EF⊂平面ABCD，Q∈HG⊂平面CDD1C1，
所以Q∈DC，也即点Q在直线DC上.
（2）根据正方体的性质可知A1B1//DC，
所以异面直线EF与A1B1所成角为∠DQE，
由于AB//DC,E,F分别是AB,BC的中点，
所以∠DQE=∠FEB=45°，
所以异面直线EF与A1B1所成角的大小为45°.
4．（2023上·上海宝山·高二校考阶段练习）在直三棱柱ABC−A1B1C1中，AC=BC=2，CC1=4，∠ACB=90°，E、F分别为棱AA1、AB的中点．
(1)求异面直线A1C与EF所成角的正切值；
(2)求三棱锥E−BCF的全面积.
【解题思路】（1）找出与A1C共面且平行于EF的直线，借助余弦定理即可得；
（2）分别计算每个面的面积，相加即可得.
【解答过程】（1）
连接A1B，因为E、F分别为棱AA1、AB的中点，
故EF为△A1BA的中位线，故EF//A1B，
故异面直线A1C与EF所成角的大小即为∠BA1C,
因为AC=BC=2，∠ACB=90°，CC1=4，
故A1A=CC1=4，AB=22+22=22，
则A1B=42+222=26，
A1C=42+22=25，
则cs∠CA1B=252+262−222×25×26=306，
即tan∠CA1B=55，
即异面直线A1C与EF所成角的正切值为55；
（2）连接BE、CE、CF，
因为BC⊥CC1、BC⊥AC，CC1∩AC=C，
CC1、AC⊂平面ACC1A1，
所以BC⊥平面ACC1A1，又CE⊂平面ACC1A1,
故BC⊥CE，又CE=22+22=22，
故S△BCE=12×2×22=22，
又CF=12AB=2，EF=12A1B=6，
则cs∠CEF=222+62−222×22×6=32，
S△CEF=12×6×22×1−322=3，
S△BCF=12S△ABC=12×12×2×2=1，
S△FBE=12S△ABE=14S△A1AB=14×12×22×4=2，
故三棱锥E−BCF的全面积S=22+3+1+2=3+32+1.
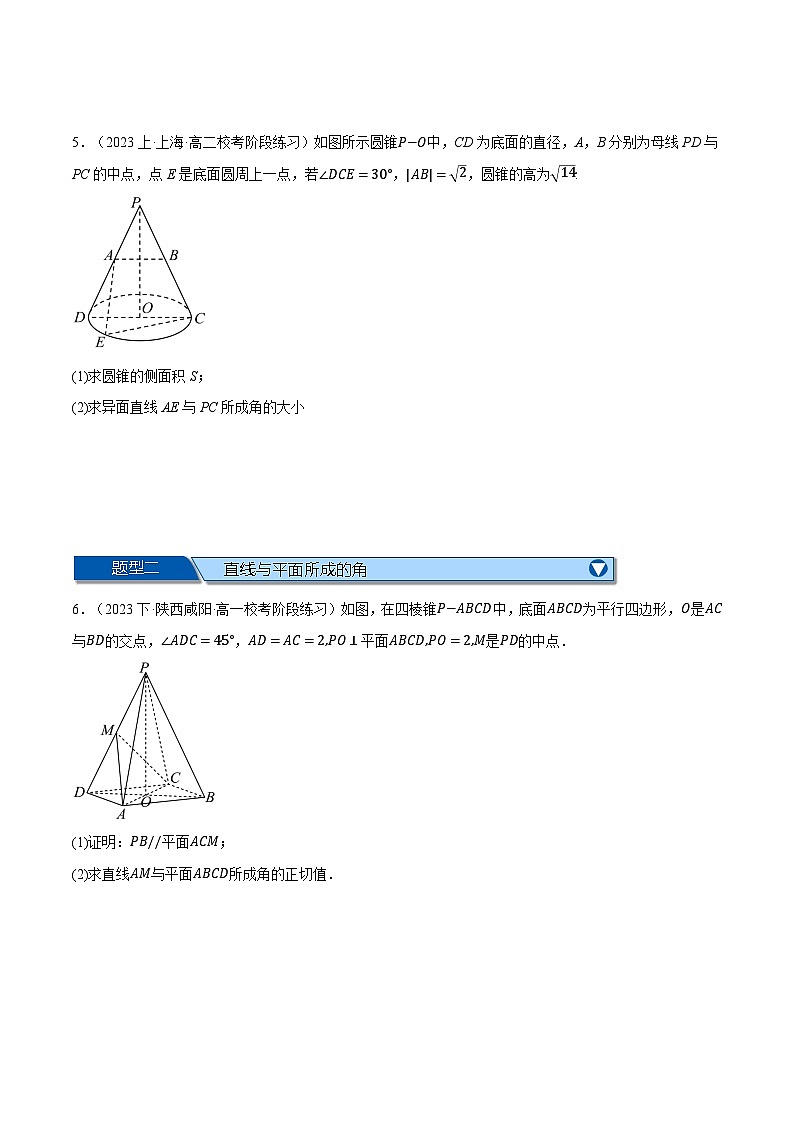
5．（2023上·上海·高二校考阶段练习）如图所示圆锥P−O中，CD为底面的直径，A，B分别为母线PD与PC的中点，点E是底面圆周上一点，若∠DCE=30°，AB=2，圆锥的高为14.

(1)求圆锥的侧面积S；
(2)求异面直线AE与PC所成角的大小
【解题思路】（1）根据已知条件求出圆锥的底面半径和母线长，然后根据圆锥的侧面积公式求解即可；
（2）连接AO,EO，可得∠EAO为异面直线AE与PC所成的角或其补角，在△AOE中，利用余弦定理求解即可.
【解答过程】（1）设圆锥底面半径为r，母线长为l，因为CD为直径，AB是△PCD的中位线，
所以r=AB=2，l=r2+PO2=2+14=4，所以侧面积S=πrl=42π.
（2）连接AO,EO，由A,O分别为PD,CD的中点，得AO//PC，
所以∠EAO为异面直线AE与PC所成的角或其补角，
在△AOE中，OA=12PC=2，OE=2，取OD中点为F，连接AF,EF，则AF=142，
EF=22−222=62，所以AE=AF2+EF2=5，
在△AOE中，cs∠EAO=5+4−22⋅2⋅5=745=7520，

所以异面直线AE与PC所成角的大小为arccs7520.
题型二
直线与平面所成的角
用向量证明线段垂直
用向量证明线段垂直
6．（2023下·陕西咸阳·高一校考阶段练习）如图，在四棱锥P−ABCD中，底面ABCD为平行四边形，O是AC与BD的交点，∠ADC=45°，AD=AC=2,PO⊥平面ABCD,PO=2,M是PD的中点．
(1)证明：PB//平面ACM；
(2)求直线AM与平面ABCD所成角的正切值．
【解题思路】（1）借助线面平行的判定定理即可得；
（2）找出直线AM与平面ABCD所成角，借助正切函数定义计算即可得.
【解答过程】（1）连接OM，
在平行四边形ABCD中，
∵O为AC与BD的交点，∴O为BD的中点，
又M为PD的中点，∴PB∥MO，
又PB⊄平面ACM,MO⊂平面ACM,∴PB//平面ACM；
（2）取DO的中点N，连接MN,AN，
∵M为PD的中点，∴MN∥PO，且MN=12PO=1，
由PO⊥平面ABCD，得MN⊥平面ABCD，
∴∠MAN是直线AM与平面ABCD所成的角，
∵∠ADC=45°,AD=AC=2,∴∠ACD=∠ADC=45°,∴∠CAD=90°，
在Rt△DAO中，AD=2,AO=12AC=1，
∴DO=5，从而AN=12DO=52，
在Rt△ANM中，tan∠MAN=MNAN=152=255，
∴直线AM与平面ABCD所成角的正切值为255．
7．（2023上·宁夏银川·高三银川一中校考阶段练习）在如图所示的直三棱柱 ABC−A1B1C1中，D、E分别是BC,A1B1的中点.
(1)求证: DE//平面ACC1A1;
(2)若△ABC为等边三角形，且AB=AA1，M为AB上的一点，AM=14AB ，求直线 DE与直线 A1M所成角的正切值.
【解题思路】（1）借助题设条件运用线面平行的判定定理求解；
（2）借助题设运用异面直线所成角的定义找出其角，再运用解三角形的方法求解．
【解答过程】（1）取AB的中点F，连接DF,EF
在△ABC中，因为D,F分别为BC,AB的中点，
所以DF//AC,DF⊄平面ACC1A1,AC⊂平面ACC1A1，
所以DF//平面ACC1A1
在矩形ABB1A1中，因为E,F分别为A1B1,AB的中点，
所以EF//AA1,EF⊄平面 ACC1A1,AA1⊂平面ACC1A1，所以EF//平面ACC1A1，
因为DF∩EF=F，DF,EF⊂平面DEF，
所以平面DEF//平面ACC1A1
因为DE⊂平面DEF，
所以DE//平面ACC1A1；
（2）因为三棱柱ABC−A1B1C1为直三棱柱，所以平面ABC⊥平面ABB1A1，
连接CF，因为△ABC为正三角形，F为AB中点，
所以CF⊥AB，平面ABC∩平面ABB1A1=AB，所以CF⊥平面ABB1A1，
取BF的中点G，连接DG,EG，可得DG//CF，故DG⊥平面ABB1A1，
又因为AM=14AB，
则A1E//MG且A1E=MG，故四边形A1EGM为平行四边形，
所以EG//A1M，
所以∠DEG即为直线DE与直线A1M所成角，
设AB=4，在Rt△DEG中，DG=12CF=3,EG=16+1=17，
所以tan∠DEG=317=5117.
8．（2023下·全国·高三校联考阶段练习）如图，在三棱台ABC−A1B1C1中，AA1⊥平面ABC，∠ABC=90°，AA1=A1B1=B1C1=1，AB=2.
(1)求证：平面ABB1A1 ⊥平面BCC1B1；
(2)求AC与平面BCC1B1所成角正弦值.
【解题思路】（1）利用线线垂直性质定理证明；
（2）将棱台补全为棱锥，利用等体积法求A到平面BCC1B1的距离，结合线平面角的定义求AC与平面BCC1B1所成角的正弦值.
【解答过程】（1）由∠ABC=90°，得AB⊥BC，
由AA1⊥平面ABC，BC⊂平面ABC，则AA1⊥BC，
又AA1∩AB=A,AA1,AB⊂平面ABB1A1，所以BC⊥平面ABB1A1，
因为BC⊂平面ABC1B1，所以平面ABB1A1 ⊥平面BCC1B1．
（2）将棱台补全为如下棱锥D−ABC，
由∠ABC=90°，AA1=A1B1=B1C1=1，AB=2，易知DA=AB=BC=2，AC=22，
由AA1⊥平面ABC，AB,AC,BC⊂平面ABC，则AA1⊥AB，AA1⊥AC，AA1⊥BC，
所以BD=22，CD=23.
可得S△BCD=12×2×22=22，
设A到平面BCC1B1的距离为h，又VD−ABC=VA−BCD，
则13×2×12×2×2=13ℎ×22，可得ℎ=2，
设AC与平面BCC1B1所成角为θ，θ∈0,π2，则sinθ=ℎAC=12.
9．（2023上·北京海淀·高三北京交通大学附属中学校考阶段练习）已知点P是边长为2的菱形ABCD所在平面外一点，且点P在底面ABCD上的射影是AC与BD的交点O，已知∠BAD=60°，△PDB是等边三角形.
(1)求证：AC⊥PD；
(2)求点D到平面PBC的距离；
(3)若点E是线段AD上的动点，问：点E在何处时，直线PE与平面PBC所成的角最大？求出最大角的正弦值，并求出取得最大值时线段DE的长.
【解题思路】（1）由题可得PO⊥平面ABCD，故PO⊥AC，根据菱形的性质可得BD⊥AC，再根据线面垂直的判定定理与性质定理即可证明；
（2）由题干数据结合VD−PBC=VP−BDC即可求解；
（3）由线面平行的判定定理可得AD∥平面PBC，可得E到平面PBC的距离即为D到平面PBC的距离，过E作垂线EF⊥平面PBC交于点F，要使角最大，则需使PE最小，此时PE⊥AD，从而求解.
【解答过程】（1）∵点P在底面ABCD上的射影是AC与BD的交点O，
∴PO⊥平面ABCD，
∵AC⊂平面ABCD，
∴PO⊥AC，
∵四边形ABCD为菱形，
∴BD⊥AC，
∵PO∩BD=O，PO、BD⊂平面PBD，
∴AC⊥平面PBD，
∵BD⊂平面PBD，
∴AC⊥PD；
（2）由题意可得△ABD､△BCD与△PBD都是边长为2的等边三角形，
∴PO=AO=CO=3，S△BDC=12×2×3=3，
∴PC=PO2+CO2=6，
∵BP=BC=2，
∴S△PBC=12×6×22−622=152，
设点D到平面PBC的距离为ℎ，
由VD−PBC=VP−BDC得13S△PBC⋅ℎ=13S△BDC⋅OP，
即152ℎ=3×3，解得ℎ=2155.
故点D到平面PBC的距离为2155.
（3）设直线PE与平面PBC所成的角为θ，
∵AD∥BC⇒AD∥平面PBC，
∴E到平面PBC的距离即为D到平面PBC的距离ℎ.
过E作垂线EF⊥平面PBC交于点F，则θ=∠EPF，
此时sinθ=EFPE=2155PE，要使θ最大，则需使PE最小，此时PE⊥AD.
由题意可知：OD=1，OA=3，
∵PO⊥平面ABCD，且PO=3，
∴PA=OP2+OA2=6，PD=OP2+OD2=2，
在△PAD中，由余弦定理可得：
cs∠PAD=AP2+AD2−PD22AP⋅AD=6+4−42×6×2=64，
∴sin∠PAD=1−cs2∠PAD=104，
由面积相等S△PAD=12AP⋅ADsin∠PAD=12AD⋅PE，
即12×6×2×104=12×2×PE，解得：PE=152，
DE=PD2−PE2=4−154=12，sinθ=45，
即点E在线段AD上靠近点D的4分点处，此时sinθ=45，DE=12.
10．（2023上·上海静安·高二上海市新中高级中学校考期中）已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2，AB=1，F为CD的中点．

(1)求证：AF//平面BCE；
(2)求证：平面BCE⊥平面CDE；
(3)求直线BF和平面BCE所成角的正弦值．
【解题思路】（1）取CE的中点G，连接FG、BG，即可证明AF//BG，从而得证．
（2）通过证明AF⊥CD，DE⊥AF，从而得到DE⊥BG，BG⊥CD，即可证明BG⊥平面CDE，进而证明平面BCE⊥平面CDE．
（3）在平面CDE内，过F作FH⊥CE于H，由平面BCE⊥平面CDE，得FH⊥平面BCE，故∠FBH为BF和平面BCE所成的角，解Rt△FHB求出∠FBH的正弦值．
【解答过程】（1）取CE的中点G，连接FG、BG．
∵F为CD的中点，∴GF//DE且GF=12DE．
∵AB⊥平面ACD，DE⊥平面ACD，
∴AB//DE，∴GF//AB．
又AB=12DE，∴GF=AB．
∴四边形GFAB为平行四边形，则AF//BG．
∵AF⊄平面BCE，BG⊂平面BCE，
∴AF//平面BCE．

（2）∵△ACD为等边三角形，F为CD的中点，∴AF⊥CD．
∵DE⊥平面ACD，AF⊂平面ACD，∴DE⊥AF．
∵BG//AF，所以DE⊥BG，BG⊥CD，
又CD∩DE=D，CD,DE⊂平面CDE，
∴BG⊥平面CDE．
∵BG⊂平面BCE，∴平面BCE⊥平面CDE．
（3）在平面CDE内，过F作FH⊥CE于H，连接BH．
∵平面BCE⊥平面CDE，平面BCE∩平面CDE=CE，FH⊂平面CDE，
∴FH⊥平面BCE．
∴∠FBH为BF和平面BCE所成的角．
因为AD=DE=2，AB=1，则FH=CFsin45°=22，BF=AB2+AF2=12+32=2，
在Rt△FHB中，sin∠FBH=FHBF=24，
∴直线BF和平面BCE所成角的正弦值为24．

题型三
求二面角
11．（2023上·四川成都·高二校考阶段练习）如图，在四棱锥P−ABCD中，底面ABCD为矩形，平面PAD⊥底面ABCD，△PAD为正三角形，E是AB的中点，AD=2,AB=4.

(1)求点C到平面PDE的距离.
(2)求二面角D−PE−C的余弦值.
【解题思路】（1）由面面垂直的性质证得AE⊥PA，根据已知求S△PDE，应用等体积法有VP−CDE=VC−PDE，即可求点面距离；
（2）由面面垂直的性质证得CD⊥PD，应用等面积法求C到PE的距离，结合二面角定义求其正弦值，进而得余弦值.
【解答过程】（1）由题设AB⊥AD，面PAD⊥面ABCD，AB⊂面ABCD，面PAD⊥面ABCD=AD，
所以AB⊥面PAD，PA⊂面PAD，故AB⊥PA，即AE⊥PA，
所以PE=PA2+AE2=22+22=22，而DE=AD2+AE2=22，PD=2，
△PDE中PD上的高7，故S△PDE=12×2×7=7，
令点C到平面PDE的距离为d，又VP−CDE=VC−PDE，且S△CDE=12×2×4=4，P到面CDE的距离为正三角形PAD的高，
所以13×7d=13×4×3，可得d=4217，故点C到平面PDE的距离为4217.
（2）由CD⊥AD，面PAD⊥面ABCD，CD⊂面ABCD，面PAD⊥面ABCD=AD，
所以CD⊥面PAD，PD⊂面PAD，故CD⊥PD，则PC=22+52=25，
又EC=22+22=22=PE，故△PCE为等腰三角形，则PC上的高为3，
令C到PE的距离为ℎ，则12×ℎ×PE=12×3×PC⇒22ℎ=215⇒ℎ=302，
由（1）知：点C到平面PDE的距离为4217，
若锐二面角D−PE−C为θ，则sinθ=4217×230=47035，故csθ=10535，
所以二面角D−PE−C的余弦值为10535.
12．（2023上·四川绵阳·高二统考期中）已知菱形ABCD的边长为2，∠BAD=60°，如图1，沿对角线BD将△ABD向上折起至△A1BD，连接A1C，构成一个四面体A1−BCD，如图2.

(1)求证：BD⊥A1C；
(2)若A1C=6，点M是A1C的中点，求平面MBD与平面BDC所成角的大小.
【解题思路】（1）取BD的中点O，连接OC,OA1，证明BD⊥OA1,BD⊥OC，可得BD⊥平面OA1C，再根据线面垂直的性质即可得证；
（2）连接OM，证明OM⊥BD，则∠MOC即为平面MBD与平面BDC所成角的平面角或补角，求出∠MOC即可.
【解答过程】（1）取BD的中点O，连接OC,OA1，
在菱形ABCD中，∠BAD=60°，则△ABD,△BCD都是等边三角形，
即在四面体A1−BCD中，△A1BD,△BCD都是等边三角形，
则BD⊥OA1,BD⊥OC，
又OA1∩OC=O,OA1,OC⊂平面OA1C，
所以BD⊥平面OA1C，
又因A1C⊂平面OA1C，
所以BD⊥A1C；
（2）连接OM，
由（1）得BD⊥平面OA1C，
因为OM⊂平面OA1C，所以OM⊥BD，
又因为BD⊥OC，平面MBD∩平面BDC=BD，
所以∠MOC即为平面MBD与平面BDC所成角得平面角或补角，
因为△A1BD,△BCD都是等边三角形，
所以OA1=OC=3，
因为A1C=6，所以A1O2+OC2=A1C2，所以OA1⊥OC，
又因点M是A1C的中点，所以∠MOA1=∠MOC=π4，
所以平面MBD与平面BDC所成角的大小为π4.

13．（2023上·海南海口·高二校考阶段练习）如图1，在梯形ABCD中，AB//CD，∠D=90°，AB=22，AD=DC=2.现将梯形ABCD沿对角线AC折成直二面角D−AC−B，如图2.
(1)求证：AD⊥平面BCD；
(2)求二面角D−AB−C的正切值.
【解题思路】（1）由勾股定理逆定理证得AC⊥BC，再利用面面垂直的性质、线面垂直的性质判定推理即得.
（2）作出二面角D−AB−C的平面角，利用几何法求出正切值即得.
【解答过程】（1）在梯形ABCD中，由AB//CD,∠D=90°,AD=DC=2，得AC=2,∠BAC=∠CAD=45°，
在△ABC中，BC2=AB2+AC2−2AB⋅ACcs45°=(22)2+22−2×22×2×22=4，
则AC2+BC2=8=AB2，有∠ACB=90°，即AC⊥BC，由直二面角D−AC−B，
得平面ACD⊥平面ABC，而平面ACD∩平面ABC=AC，BC⊂平面ABC，
于是BC⊥平面ACD，而AD⊂平面ACD，则AD⊥BC，又AD⊥CD,CD⊥BC=C,CD,BC⊂平面BCD，
所以AD⊥平面BCD.
（2）取AC中点O，过O作OE⊥AB于E，连接OD,DE，
由AD=DC=2，得OD⊥AC，又∠CAD=45°，则OA=OD=1，
又平面ACD⊥平面ABC，而平面ACD∩平面ABC=AC，OD⊂平面ACD，则OD⊥平面ABC，
而AB⊂平面ABC，则OD⊥AB，又OD∩OE=O,OD,OE⊂平面DOE，
于是AB⊥平面DOE，而DE⊂平面DOE，则DE⊥AB，因此∠DEO是二面角D−AB−C的平面角，
OE=OAsin45°=22，在Rt△DOE中，tan∠DEO=ODOE=2，
所以二面角D−AB−C的正切值是2.
14．（2023上·山东潍坊·高三校考阶段练习）如图所示，在四棱锥P−ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，E，F分别是线段AB，BC的中点.

(1)证明：PF⊥FD；
(2)若PB与平面ABCD所成的角为45°，求二面角P−FD−C的余弦值.
【解题思路】（1）根据勾股定理的逆定理，结合线面垂直的性质和判定定理进行证明即可；
（2）根据二面角的定义，结合锐角三角函数定义进行求解即可.
【解答过程】（1）连接AF，则AF=2，又DF=2，AD=2，
∴DF2+AF2=AD2，∴DF⊥AF，
∵PA⊥平面ABCD，DF⊂平面ABCD，
∴PA⊥DF，
又PA∩AF=A,PA,AF⊂平面PAF，
∴DF⊥平面PAF，又PF⊂平面PAF，
∴DF⊥PF；
（2）∵PA⊥平面ABCD，∴∠PBA是PB与平面ABCD所成的角，
且∠PBA=45°．∴PA=AB=1，
∵DF⊥平面PAF，∴DF⊥PF， DF⊥AF，
∴∠PFA为平面PFD与平面CFD所成锐角，
∴cs∠PFA=AFPF=23=63，
故二面角P−FD−C的余弦值为−63.
15．（2023上·湖北·高三湖北省天门中学校联考期中）如图，在四棱锥P−ABCD中，底面ABCD是平行四边形，E，F分别为AB，PD上的点，且BECD+PFPD=1.

(1)证明：AF//平面PCE；
(2)若PD⊥平面ABCD，E为AB的中点，PD=AD=CD，∠BAD=60°，求二面角P−CE−F的正切值.
【解题思路】（1）在CD上取一点G，使得CG=AE，可证FG//平面PCE，再证AG//平面PCE，可得平面AFG//平面PCE，得证；
（2）由题意建系用向量法求解或用几何法找出二面角的平面角求解.
【解答过程】（1）如图，在CD上取一点G，使得CG=AE，
连接AG，FG，因为BECD+PFPD=1，且ABCD是平行四边形，
所以PFPD=1−BECD=CGCD，故FG//PC，
又因为PC⊂平面PCE，FG⊄平面PCE，
所以FG//平面PCE，
因为ABCD是平行四边形，且CG=AE，
所以AECG是平行四边形，故AG//EC，
又因为EC⊂平面PCE，AG⊄平面PCE，
所以AG//平面PCE，
因为AG∩FG=G，且AG⊂平面AFG，FG⊂平面AFG，
所以平面AFG//平面PCE，
因为AF⊂平面AFG，
所以AF//平面PCE.

（2）方法1：当E为AB中点，PD=AD=CD，∠BAD=60°时，
易知DE⊥CD，F为PD中点，又因为PD⊥平面ABCD，
所以DE，DC，DP两两互相垂直，
则以D为坐标原点，DE为x轴，DC为y轴，DP为z轴建立坐标系，
设PD=AD=CD=2，则C(0,2,0)，E3,0,0，F(0,0,1)，P(0,0,2)，
所以CE=3,−2,0，FE=3,0,−1，PE=3,0,−2.
设平面FCE与平面PCE的法向量分别为m=x1,y1,z1，n=x2,y2,z2，则
3x1−2y1=03x1−z1=0，3x2−2y2=03x2−2z2=0，
不妨取x1=3，x2=3，则m=3,32,3，n=3,32,32，
所以csm,n=m⋅nmn=13190，
故二面角P−CE−F的正弦值为1−169190=21190，正切值为2119013190=2113.
方法2：过D作DM⊥EC，垂足为M，分别连接PM，FM，ED，

因为PD⊥平面ABCD，EC⊂平面ABCD，
所以PD⊥EC，
因为PD，DM是平面PDM内两相交直线，
所以EC⊥平面PDM，
因为PM⊂平面PDM，FM⊂平面PDM，
所以EC⊥PM，EC⊥FM，
即∠PMF就是二面角P−CE−F的平面角，
设∠PMF=α，∠PMD=∠1，∠FMD=∠2，
因为E为AB的中点，BECD+PFPD=1，底面ABCD是平行四边形，
所以F是PD中点，
设PD=AD=CD=2，
因为∠BAD=60°，易知DE⊥CD，且ED=3，
所以EC=CD2+ED2=7，
所以sin∠ECD=EDEC=217，
所以DM=2sin∠ECD=237，
所以tan∠1=PDDM=73，tan∠2=FDDM=723，
所以tanα=tan∠1−∠2=tan∠1−tan∠21+tan∠1⋅tan∠2=2113，
即二面角P−CE−F的正切值为2113.
题型四
求点面距离
16．（2023下·河南洛阳·高一校考阶段练习）如图，四棱锥P−ABCD中，底面ABCD为平行四边形，∠ABC=60°，PA⊥平面ABCD，E为PD的中点.
(1)证明：PB//平面AEC；
(2)设AD=2，PA=AB=1，求点D到平面AEC的距离.
【解题思路】（1）借助线面平行的判定定理即可得；
（2）借助等体积法与体积公式计算即可得.
【解答过程】（1）连接BD，交AC于点O，连接OE，
∵四边形ABCD是平行四边形，∴O是BD的中点，
又∵E为PD的中点，∴OE是三角形PBD的中位线，∴PB//OE，
又∵PB⊂平面AEC，OE⊂平面AEC，∴PB//平面AEC；
.
（2）∵平行四边形ABCD中，∠ABC=60°，BC=AD=2，AB=1，
∴AC=AB2+BC2−2AB⋅BCcs∠ABC=3，
则AC2+AB2=BC2，故∠ACD=90°，
又∵PA⊥平面ABCD，∴△PAB，△PAD，△PAC都是直角三角形，
∵PA=AB=1，∴PB=2，PC=2，PD=5，
∴PD2=PC2+CD2，∴∠PCD=90°，∴EA=EC=52，
因为O是AC的中点，所以OE⊥AC，且OE=12PB=22，
所以S△EAC=12AC⋅OE=12×3×22=64，
S△DAC=12AC⋅CD=12×3×1=32，
设点D到平面AEC的距离为ℎ，
由VD−ACE=VE−ACD=12VP−ACD得：13×64×ℎ=12×13×32×1，
解得ℎ=22.
17．（2023下·全国·高三校联考阶段练习）如图，四棱锥P−ABCD中，底面ABCD为直角梯形，AB//CD，∠ABC=90°，AB=4，BC=CD=2，△PAD为等边三角形，BD⊥PA．

(1)证明：BD⊥平面PAD；
(2)求点C到面PBD的距离．
【解题思路】（1）取AB中点E，连DE，易得EBCD为正方形，△AED为等腰直角三角形，再根据线面垂直的判定得证.
（2）取AD中点O，连PO，由线面垂直的判定有PO⊥平面ABCD，根据三棱锥体积公式求三棱锥C−PBD的体积，再根据等体积法求出点C到平面PBD的距离.
【解答过程】（1）取AB中点E，连DE，因为AB//CD，∠ABC=90°，AB=4，BC=CD=2，
所以四边形EBCD为正方形，△AED为等腰直角三角形，则∠ADE=45∘,∠BDE=45∘,
得，∠ADE+∠BDE=90∘，故BD⊥AD，

因为BD⊥PA，PA∩ AD=A，PA，AD⊂平面PAD，
所以BD⊥平面PAD
（2）设点C到平面PBD的距离为h,由（1）得PD=BD=22，BD⊥PD，
则△BDP面积为12PD⋅BD=4，
取AD中点O，连PO，则PO⊥AD，且PO=6，
因为BD⊥平面PAD， PO⊂平面PAD，
所以BD⊥PO，AD∩BD=D，AD，BD⊂平面ABCD，
所以PO⊥平面ABCD，
又△BCD面积为12BC⋅BD=2，
三棱锥C−PBD的体积为VC−PBD=13S△BDP⋅ℎ=VP−BCD=13S△BCD⋅PO=263，
得ℎ=62.即点C到平面PBD的距离62.
18．（2023上·宁夏石嘴山·高三平罗中学校考阶段练习）如图，在长方体ABCD−A1B1C1D1中，AD=AB=2，BD1和B1D交于点E，F为AB的中点．
(1)求证：EF//平面ADD1A1；
(2)已知B1D与平面ABCD所成角为π4，求点A到平面CEF的距离．
【解题思路】（1）连接AD1,BD，证明EF//AD1，根据线面平行的判定定理即可证明结论；
（2）连接EA、AC，设BD、AC相交于点O，根据VE−ACF=VA−CEF，可求得答案.
【解答过程】（1）连接AD1,BD，在长方体ABCD−A1B1C1D1中，DD1//BB1,DD1=BB1，
故四边形DD1B1B为平行四边形，则E为BD1的中点，
又F为AB的中点，故EF//AD1，而EF⊄平面ADD1A1,AD1⊂平面ADD1A1，
故EF//平面ADD1A1；
（2）在长方体ABCD−A1B1C1D1中，AD=AB=2，则四边形ABCD为正方形，
则BD=22，又BB1⊥平面ABCD，则∠B1DB为B1D与平面ABCD所成角，
即∠B1DB=π4，故BB1=BD=22，
连接EA、AC，设BD、AC相交于点O，所以点O为BD中点，
因为DD1//EO，EO=12DD1=2，可得EO⊥底面ABCD，连接OF，
S△ACF=12AF×BC=12×1×2=1，所以VE−ACF=13S△ACFEO=13×1×2=23，
OF=12AD=1，OC=12AC=12BD=2，
EF=EO2+OF2=2+1=3，EC=EO2+OC2=2+2=2，
FC=BF2+BC2=1+4=5，
在△EFC中，由余弦定理得cs∠FEC=EF2+EC2−FC22EF×EC=3+4−523×2=36，
因为0