专题6.6 解三角形-2023-2024学年高一数学下学期高效讲练测（人教A版必修第二册）

这是一份专题6.6 解三角形-2023-2024学年高一数学下学期高效讲练测（人教A版必修第二册），文件包含专题66解三角形举一反三人教A版必修第二册原卷版docx、专题66解三角形举一反三人教A版必修第二册解析版docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。

TOC \ "1-3" \h \u
\l "_Tc29132" 【题型1 余弦定理边角互化的应用】 PAGEREF _Tc29132 \h 4
\l "_Tc17130" 【题型2 余弦定理解三角形】 PAGEREF _Tc17130 \h 5
\l "_Tc7605" 【题型3 正弦定理边角互化的应用】 PAGEREF _Tc7605 \h 7
\l "_Tc3026" 【题型4 正弦定理判定三角形解的个数】 PAGEREF _Tc3026 \h 8
\l "_Tc19245" 【题型5 正弦定理解三角形】 PAGEREF _Tc19245 \h 10
\l "_Tc8311" 【题型6 三角形面积公式的应用】 PAGEREF _Tc8311 \h 11
\l "_Tc5430" 【题型7 正、余弦定理判定三角形形状】 PAGEREF _Tc5430 \h 13
\l "_Tc3348" 【题型8 正、余弦定理在几何图形中的应用】 PAGEREF _Tc3348 \h 15
\l "_Tc18266" 【题型9 距离、高度、角度测量问题】 PAGEREF _Tc18266 \h 20
【知识点1 余弦定理、正弦定理】
1．余弦定理
(1)余弦定理及其推论的表示
(2)对余弦定理的理解
①余弦定理对任意的三角形都成立.
②在余弦定理中，每一个等式都包含四个量，因此已知其中三个量，利用方程思想可以求得未知的量.
③余弦定理的推论是余弦定理的第二种形式，适用于已知三角形三边来确定三角形的角的问题.用余弦
定理的推论还可以根据角的余弦值的符号来判断三角形中的角是锐角还是钝角.
④余弦定理的另一种常见变式：+-=2bcA，+-=2acB，+-=2abC.
2．正弦定理
(1)正弦定理的表示
在△ABC中，若角A,B,C对应的边分别是a,b,c，则各边和它所对角的正弦的比相等，即==.
(2)正弦定理的常见变形
在△ABC中，由正弦定理得===k(k>0)，则a=kA，b=kB，c=kC，由此可得
正弦定理的下列变形：
①=，=，=，aB=bA，aC=cA，bC=cB；
②======；
③a:b:c=A:B:C；
④===2R，（R为△ABC外接圆的半径）.
(3)三角形的边角关系
由正弦定理可推导出，在任意三角形中，有“大角对大边，小角对小边”的边角关系.
3．解三角形
(1)解三角形的概念
一般地，三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.在三角形中，已知三角形的几个
元素求其他元素的过程叫做解三角形.
(2)余弦定理在解三角形中的应用
利用余弦定理可以解决以下两类解三角形的问题：
①已知两边及它们的夹角，求第三边和其他两个角；
③已知三边，求三角形的三个角.
(3)正弦定理在解三角形中的应用
公式==反映了三角形的边角关系.
由正弦定理的推导过程知，该公式实际表示为：=，=，=.上述的
每一个等式都表示了三角形的两个角和它们的对边的关系.从方程角度来看，正弦定理其实描述的是三组方程，对于每一个方程，都可“知三求一”，于是正弦定理可以用来解决两类解三角形的问题：
①已知两角和任意一边，求其他的边和角，
③已知两边和其中一边的对角，求其他的边和角.
4．对三角形解的个数的研究
已知三角形的两角和任意一边，求其他的边和角，此时有唯一解，三角形被唯一确定.
已知三角形的两边和其中一边的对角，求其他的边和角，此时可能出现一解、两解或无解的情况，三
角形不能被唯一确定.
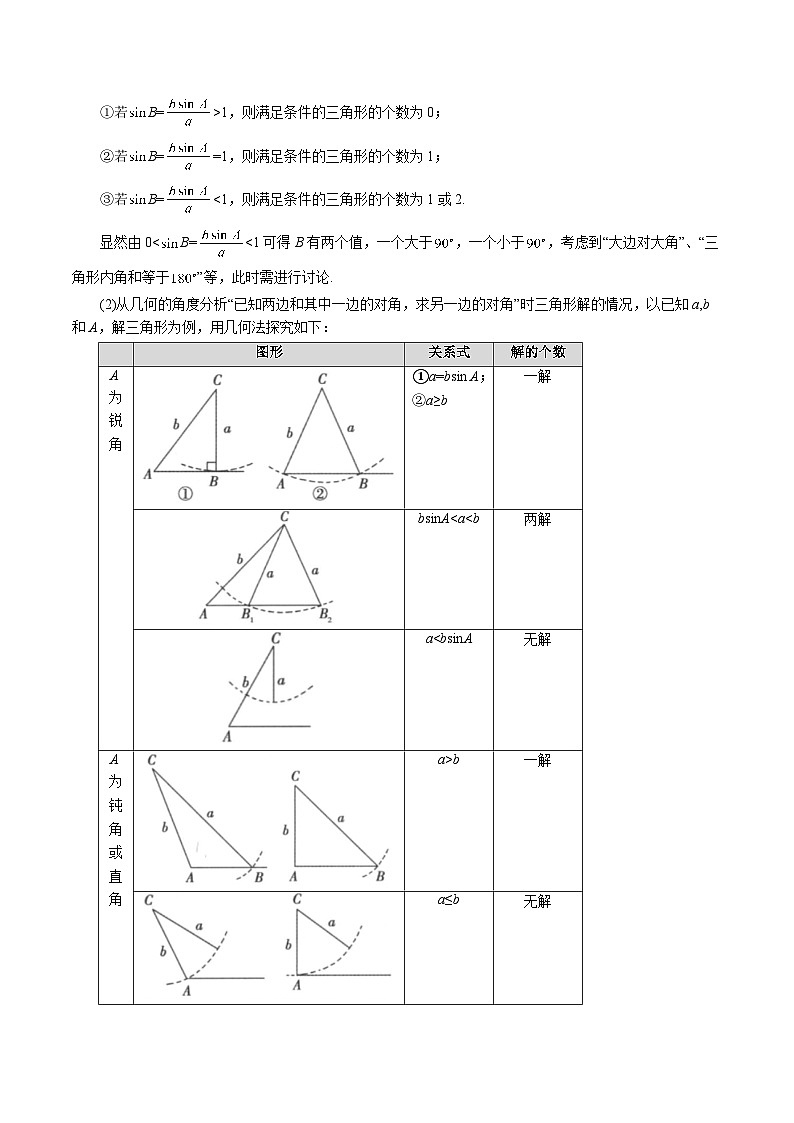
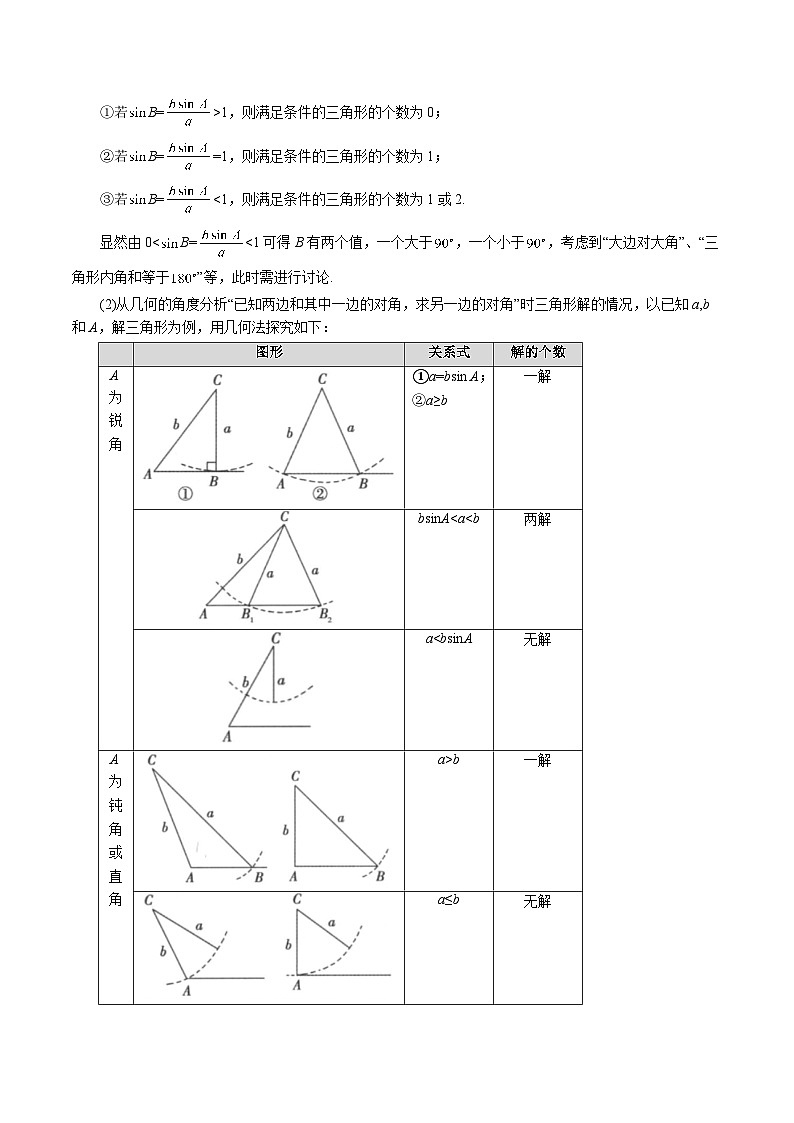
(1)从代数的角度分析“已知两边和其中一边的对角，求另一边的对角”时三角形解的情况，下面以已知
a,b和A，解三角形为例加以说明.
由正弦定理、正弦函数的有界性及三角形的性质可得：
①若B=>1，则满足条件的三角形的个数为0；
②若B==1，则满足条件的三角形的个数为1；
③若B=